Динамические и квалиметрические модели оценки качества жизни семьи

С оциально-экономические преобразования в России 1990 — 2000-х годов неблагоприятно повлияли на жизнедеятельность большей части населения. Снижение реальных доходов вынудило значительную часть семей ограничить удовлетворение практически всех потребностей. Обычным явлением стали неполные семьи, незарегистрированные браки, семьи, где воспитываются внебрачные дети. Репродуктивная функция реализуется в редуцированном виде: число рожденных детей оказывается значительно меньше желаемого и заметно меньше идеального. Затруднительно исполняются функции семьи — хозяйственно-бытовая, материальноэкономическая, досуговая, коммуникативная, социального контроля, сексуальная и т.д.

В современных исследованиях проблем семьи прослеживается дифференцированный подход, учитывающий конкретные условия жизни в регионах и этнические особенности.

Необходимость исследований региональной специфики условий жизнедеятельности семьи диктуется также существующим неравенством регионов Российской Федерации в социально-экономическом развитии, дифференциацией населения по уровню дохода, в доступности образования и медицинской помощи [1]. Изучение изменений, происходящих в жизнедеятельности семей и в выполнении семейных функций, важно для разработки рекомендаций в области семейно-демографичеcкой политики.

В данном исследовании семья рассматривается в аспекте социально-демографической динамики и с позиций семейной квалиметрии. Динамика прослеживается через процессы смены состояний жизни семьи, изменение показателей здоровья, качества жизни, удовлетворенности ее отдельными сторонами.

Квалиметрическая оценка позволяет количественно характеризовать качество объектов различной природы, например, качество жизни рассматривать как интегральный показатель-функцию отдельно измеряемых свойств объекта.

В социологических исследованиях применяются три подхода к оцен- ке качества жизни: измерение объективных показателей, получение субъективных оценок и комплексный подход [2; 3]. Объективная модель качества жизни соответствует ква-лиметрической оценке, поскольку качество определяется по совокупности различных статистических показателей — индикаторов: природногеографических, экологических, экономических, социальных, демографических и т.д. Согласно субъективной модели, истинное понимание качества жизни отражено в субъективных ощущениях индивидов, которые формируются на основе уровня интеллектуального развития индивида, его жизненного опыта, эмоционального состояния и т.д. Субъективные индикаторы качества жизни подразделяют на две компоненты — когнитивную (рациональную) и аффективную (эмоциональную) [3]. В комплексной модели качества жизни учитывается взаимосвязь объективных и субъективных показателей жизнедеятельности людей [2]. Для отображения этой взаимосвязи также используются квалиметрические модели, когда интегральные показатели качества жизни рассчитываются по субъективным оценкам, полученным в ходе социологических опросов. Вычисление интегральной оценки, расчет комплексного показателя является сложнейшей проблемой объединения частных оценок.

Модели исследования

Закономерности естественного перемещения населения в многомерном пространстве различных временных, географических и иных количественных характеристиках состояния отражаются обобщенным уравнением динамики МакКендрика — Фон Фестера [4; 5]:

д N д N д ( vN )

— + — +------= - ц (t, т ,x ) N ( t , т , x ) , (1)

∂t ∂τ    ∂x где в данном случае:

N ( t, т ,x ) — выражает возрастную (по τ ) и медико-демографическую ( x ) структуру населения различных социальных групп , изменяющуюся во времени t;

д ( t, т ,x ) — коэффициент смертности, зависящий от показателя состояния здоровья; x — шкала показателя состояния здоровья населения ( x= 0 — неизлечимо больное население);

v ( t,τ, x ) — скорость изменения состояния здоровья, зависящая от возраста и наличного здоровья.

Под переменной x можно понимать любой показатель качества жизни или набор этих показателей. В последнем случае количество слагае- д( vN)

мых вида       в левой части урав-

∂x нения (1) увеличивается на число дополнительных переменных x.

Модель динамической системы, построенная по аналогии со схемами А. МакКендрика и соответствующая уравнению (1), отражает сетку смены состояний по возрасту τ и характеристикам качества жизни x с учетом гибели части элементов популяции в каждом состоянии ( τ, x ).

Смена возрастных состояний протекает в одном направлении.

Состояние здоровья изменяется от максимальной величины (здоровые люди) до x= 0 (неизлечимо больные) в обоих направлениях, поскольку человек может заболеть или излечиться за исключением случая x= 0.

Скорость v ( t,τ, x ) является разностью скоростей этих взаимных потоков и может принимать положительные и отрицательные значения. При v> 0 преобладает процесс излечения.

Для решения уравнения (1) необходимо задать начальные N H ( т , x ) = N (0, т , x ) (первичное t= 0 распределение населения по характеристикам состояния ( т , x )) и граничные условия N ₀ = N ( t ,0, x ) , соответствующее распределению числа новорожденных по состоянию здоровья в год t:

Nо(t,x) = Ив(t,т,y,x)N(t,т,y)dydT , (2) τy где в(t,т,y, x) — относительный показатель рождаемости детей с состоянием здоровья x у людей в возрасте τ со здоровьем y.

Основной груз нездоровья ребенок приносит с собой при рождении, и факторами, влияющими на его формирование, являются состояние здоровья родителей, прежде всего, матери, витальность ее поведения, качество объективных условий проживания (доходы, жилье), а также психоэмоциональное отношение матери к ожиданию и рождению ребенка [6]. Это уравнение генерирует обратную связь в модели динамики населения, что обеспечивает устойчивость воспроизводства поколений.

Динамические процессы реализуются на разных уровнях общественной организации: отдельный человек, семья, группа, сообщество, территориальная общественная система (население). Уравнение (1) приемлемо для описания этих процессов на всех уровнях, но со специфическим смыслом трактовки переменных состояния.

Изменения могут иметь непрерывный и дискретный характер, отражать детерминированные и вероятностные процессы и т.д.

При статистической трактовке динамики семьи по показателям возраста и здоровья переходим к показателю плотности вероятности (частоте) P ( t, т ,x ) = N ( t, т ,x ) / N (0, т ,x ), отражающей судьбу поколения в пространстве ( т , x ) в среднем для данного региона. Величина P ( t, т ,x ) выступает в качестве своеобразной эффективности жизнедеятельности данного поколения рождения t-τ года — вероятность в момент t в возрасте τ иметь здоровье на уровне x.

Уравнение (1) имеет широкое применение [7; 8] при исследовании динамики потоковых систем в различных областях науки, где переменная функция N ( t, т ,x ) и ее аргументы трактуются разным способом. Результаты использования для анализа уравнения (1) во многом зависят от вида функций ц (t, т ,x ) и v ( t,т), а также количественных значений характеристик состояния здоровья x. Для вычисления x привлекаются различные методы статистического анализа [9].

Для примера рассмотрим случай постоянных значений µ и v . Два первых интеграла f 1 и f 2 решения уравнения (1) соответствуют формулам

• a )    N = f i ехр( - дт ), б ) x = v т + f 2 . (3)

Переменные f1 и f2 выражают некоторые законы сохранения, принимая постоянные значения на любом решении уравнения (1); эти значения однозначно характеризуют ситуацию, например, f1 = N0 — начальная численность популяции, f2 = x0 — первоначальное состояние здоровья. Выражения (3) отражают естественные законы, в частности, равенство (3а) означает, что численность одновозрастной популяции с возрастом не увеличивается (при µ≥0), а равенство (3б) утверждает, что здоровье с возрастом ухудшается (v<0).

Действительно, в исследовании Н.М. Римашевской с соавторами [9] такая связь соответствует уравнению x = -0,02 т +4,0, и она учитывает влияние возраста τ как главного фактора здоровья x . В данном примере начальное здоровье x о = 4 (значение первого интеграла f 2 ), и этот ресурс может постепенно расходоваться в течение т т = 4,0/0,02 = 200 лет. Постоянная величина временного ресурса 50 x + т = 200 пропорционально распределяется между показателями возраста и здоровья.

В том случае, если в уравнении (1) вместо x учитывается несколько характеристик состояния x i и x j со скоростями изменения v i и v j , то по аналогии с (3б) справедливы соотношения

a) x i ^{- x} 0 i = — ⁽ x j ^{- x} 0 j ) , v j

• б )    f j= ^ — x = T mi -T mj , (4) v_i v_j

где сохраняющийся первый интеграл fij определяется разностью временных ресурсов по каждой частной характеристике fj = Tmi - Tmj и специ- альными значениями x0i и x0j, отражающими первичные обстоятельства формирования связей.

Центрированные относительно них величины xi и xj согласно (4а) пропорциональны с коэффициентом пропорциональности Сij =vi/vj, равном соотношению скоростей изменения характеристик. Причем это справедливо и для переменных скоростей изменения с постоянной величиной коэффициента Cij. Иными словами, выполняется закон, что центрированные значения взаимно обусловлены:

xi^{- x} 0 i = C ij ⁽ x j ^{- x} 0 j ) .      ⁽⁵⁾

В динамических моделях вида (1)

вместо нескольких частных показателей xi удобней использовать одну интегральную

кардиналистскую

оценку x состояния , удовлетворяющую уравнению Эйлера для смещенных значений переменных:

x - x ₀

= У ^ai ⁽ x i ^{- x} 0 i ), ^ai =^ x- . ⁽⁶⁾ _i                        ∂ x i

Это уравнение генерирует обрат- ную связь, лежащую в основе самоорганизации социально-демографической системы из разных частей и характеристик xi, факторов xi и условий x0i, обстоятельств xi и обязательств ai (чувствительностей) ее существования. Оценка x является квалиметри-ческой, т.е. становится результатом косвенного измерения с расчетом значения по измерениям частных показателей качества. Первые интегралы ^i уравнения (6) дают соотношения, аналогичные (5):

x i ^{- x} 0 i = V i^{(x - x} 0) . ⁽⁷⁾

Отсюда при C ij =ϕ i /ϕ j возникает равенство (5). Следовательно, динамические и квалиметрические модели в теоретическом плане дают сходные результаты, но с разной интерпретацией содержания базовых связей.

Методы исследования

Качество жизни людей в огромной степени зависит от условий жизнедеятельности, состояния брачносемейных отношений и здоровья. Ос- новываясь на общепринятой методологии качество жизни можно оценить по «объективным» (жилищные условия, уровень дохода и др.) и по «субъективным» параметрам (уровень удовлетворенности условиями жизни, самооценка здоровья и др.) благополучия.

В частности, уровень жизни можно определить точнее, если учитывать не только уровень дохода субъекта и семьи, но и уровень самооценки ими степени материального благополучия, места в социальной иерархии. Это аналогично тому, как уровень здоровья можно охарактеризовать по «объективному» состоянию, определяемому по результатам анализов, так и на основе субъективных оценок человека.

Понятие «удовлетворенность» в основном трактуется как субъективная (позитивная) оценка обстоятельств окружающей действительности (ситуации). В социологии семьи распространено представление о том, что удовлетворенность семейной жизнью может быть важнейшей характеристикой «стабильности семьи» [10].

Определение степени удовлетворенности жизнью в зависимости от удовлетворенности работой, образованием, доходом, здоровьем, использованием времени и удовлетворенностью браком и семьей широко ис- пользуется в социальных исследованиях.

Для количественной оценки удовлетворенности выстраивается шкала порядка (ординации), в которой объекты упорядочены по рангам (занимаемым местам) в зависимости от свойств измеряемых объектов в их отношениях «больше-меньше», «лучше-хуже» и т.п. Каждому рангу сопоставляется число (балл) в порядке возрастания или снижения положения. Для таких чисел допускаются операции линейного сравнения вида (7), что позволяет представить частные характеристики x i через модельные x .

Модельным эквивалентом качества жизни в его субъективном выражении удовлетворенности можно считать степень благополучия — состояние человека и соответствующая ситуация со стечением обстоятельств, которые благоприятно характеризуют его жизнь в глазах окружающих.

В этом смысле «качество жизни семьи» можно измерить в баллах по шкале порядка «благополучие — неблагополучие» (табл. 1).

Большему баллу x i в данном случае соответствует высокий уровень удовлетворенности. По этой причине интегральный показатель качества жизни x должен повышаться ( a i >0) при росте x i .

Таблица 1

Принятая шкала порядка «благополучие — неблагополучие» в баллах (0-4)

Уровень благополучия	Баллы
Благополучие	4
Относительное благополучие или умеренное неблагополучие	3
Средний уровень неблагополучия	2
Высокий уровень неблагополучия	1
Очень высокий уровень неблагополучия	0

Через отображение (7) x→ xi при ϕi =1, x0i = x0 = 0 вводится шкала порядка частных характеристик, например, по критерию обеспеченности жилищными условиями (табл. 2). Неудовлетворенность жизнью в этом отношении свойственна большому числу семей. По данным Росстата, средняя обеспеченность жильем составляет 22,8 кв. м. на человека, и наблюдается заметная дифференциация семей по уровню жилищных условий [11].

Различия в жилищных условиях сильно зависят от демографических типов домохозяйств.

Критичные жилищные условия наблюдаются в многодетных семьях и семьях, имеющих расширенную структуру.

Таблица 2

Шкала порядка по критерию обеспеченности жилищными условиями

Характеристика жилищных условий	Оценка степени благополучия	Баллы
Нет собственного жилья (снимают жилплощадь)	Высокий уровень неблагополучия	1
Проживают в общежитии или в квартире на несколько семей	Относительное благополучие/ умеренное неблагополучие	3
Проживают в собственной квартире или частном доме	Благополучие	4

Таким образом, через ордина-листский показатель благополучия единообразно вводятся и оцениваются разные характеристики (компоненты) качества жизни x i .

В состав объективной компоненты входят оценки жилищных условий ( x 1 — наличие собственного жилья, x 2 — тип домохозяйства), x 3 — уровня cреднедушевого дохода (в расчете на одного члена семьи в сравнении с бюджетом прожиточного минимума), x 4 — количество детей в семье (в худшем положении x 4 =1 находятся многодетные семьи).

В состав субъективной компоненты входят: x5 — субъективная оценка (самооценка) материального благополучия, x6 — самооценка социального статуса, x7 — самооценка состояния здоровья, x8 — причины занятости женщины, x9 — удовлетворённость своей работой, x10 — удо- влетворенность условиями жизни в регионе.

Учтены показатели психоэмоционального напряжения и его источники ( x 11 — уровень психоэмоционального стресса (тест Ридера), x 12 — удовлетворенность жизнью в целом, x 13 — удовлетворенность условиями жизни, x 14 — удовлетворение основных жизненных потребностей), а также уровни x 15 — общей семейной тревоги, x 16 — удовлетворенности интимно-сексуальными отношениями, x 17 — эмоциональной поддержки, x 18 — общности интересов.

Для получения информации об условиях жизнедеятельности и процессах, происходящих в современной семье, проживающей в городах Иркутской области, были проведены социологические исследования среди семейного населения.

В исследовании приняли участие жители городов с высокой концен- трацией промышленных объектов и образовательных учреждений. Объем выборки взят с учетом численности генеральной совокупности (около 100000 человек) и составил не менее 400 единиц, в соответствии с рекомендациями для подобного рода исследований [12]. В категорию семейного населения вошли 158 мужчин (средний возраст 28,8±3,6 лет) и 292 женщины (средний возраст 28,7±2,7 лет), имеющие детей дошкольного возраста и находящиеся в наиболее активном репродуктивном возрасте (18-35 лет). Для их опроса был применен многоступенчатый метод: вначале случайным образом отбиралось дошкольное учреждение, затем — группа пребывания детей, на третьем этапе — родители, относящиеся к возрастной группе 18-35 лет. Относительно равномерное распределение обследованных дошкольных учреждений по районам городов позволило опросить представителей различных социально-профессиональных групп.

Опрос проводился по специально разработанной анкете, включающей следующие блоки вопросов: «Жилищные условия и уровень жизни семьи», «Семья» (тип, состав семьи, число детей в семье, число членов семьи, брачный статус и поведение; репродуктивные установки рождения детей); «Работа» (занятость женщин, отношение к работе), «Миграция» (удовлетворенность условиями жизни в регионе, планы на переезд). При разработке анкеты и проведении социологического опроса респондентов использовались подходы, учитывающие многолетний опыт подобных исследований отечественными учеными [13; 14].

В качестве измерителя уровня индивидуального здоровья исполь- зована методика его самооценки, рекомендованная ВОЗ для мониторинга здоровья населения, по пятибалльной шкале от 5 баллов (отличное) до 1 балла (очень плохое).

Психодиагностика семейного населения проведена медицинским психологом М.В. Кулешовой с использованием опросника «Ролевые ожидания и притязания в браке (РОП)» и опросника «Анализ семейной тревоги» [15]. Уровни психосоциального стресса, удовлетворенности жизнью в целом, удовлетворенности условиями жизни, удовлетворенности основных жизненных потребностей оценивали по методике О.С. Копиной [16].

Результаты исследования

Оценка всех основных сфер жизнедеятельности семьи (семейнобытовые и социально-экономические условия, психосоциальное благополучие) показала, что жилищные условия у 70,8% опрошенных были удовлетворительными: они проживали в собственном доме или в отдельной квартире. В коммунальной квартире — 9,0%, в общежитии — 5,8% и не имели собственного жилья и снимали жилплощадь 14,4% респондентов. Жилищная обеспеченность 68,3% семей из трех и более человек менее федерального стандарта социальной нормы жилья (18 кв. метров на одного члена семьи). В двухкомнатной квартире проживали 38,5% семей, в трехкомнатной — 29,7%, в однокомнатной — 27,1%, менее 5% имели четырехкомнатную квартиру.

Большинство (78,2%) составляли нуклеарные домохозяйства (семейная пара с детьми) Из числа сложных семей с родителями жены проживали 10,3%, с родителями мужа — 5,9%, с другими родственниками — 5,6%. Неполные семьи составляли 4,7%.

• 95 ,9% семей — малодетные (1-2 ребенка), из них 69,1% имеют одного ребёнка; 2,9% — трехдетные, в остальных семьях более четырех детей.

Распределение семей по душевому доходу в соотношении с прожиточным минимумом (ПМ) имело следующий вид: группа семей с душевым доходом ниже ПМ составляла 22,1%; от 1 до 2 ПМ — 34,8%; от 2 ПМ до 3 ПМ — 31,8%; свыше 3 ПМ — 11,3%.

Уровень благосостояния семей непосредственно связан с числом детей. Трехдетные семьи в группе бедных с душевым доходом ниже ПМ встречались почти в 2 раза чаще, чем одно- и двухдетные семьи.

Самооценка материального статуса семьи у женщин ниже, чем у мужчин. Они чаще указывали, что вынуждены занимать деньги и жить в «долг». В то же время при самооценке экономического статуса семьи особых различий не выявлено: более 40% опрошенных считали свою семью «недостаточно обеспеченной» и более 30% — «обеспеченной».

Анализ причин, по которым женщина вынуждена работать, показал, что 46,5% женщин работают по материальным соображениям, 24,7% — считают, что женщина должна работать наравне с мужчиной; только 19,9% женщин могут оставить работу, если этого потребуют интересы семьи; 8,8% женщин выбрали иной ответ. Довольно близким к этому было распределение мнений мужчин о необходимости работы в их семье женщины.

На момент опроса условия жизни в Иркутской области устраивали 40,1% мужчин и 32,0% женщин, отчасти устраивали 41,0% мужчин и

44,1% женщин, не устраивали 19,7% и 23,1% соответственно. При этом большинство опрошенных были недовольны высокой стоимостью жизни (44,1% мужчин и 34,2% женщин); неблагоприятным климатом (22,8% и 21,9%, соответственно); географической отдаленностью региона (6,7% и 9,1%). Остальных респондентов не устраивало все вышеперечисленное.

Анализ самооценки здоровья выявил более высокие уровни среди мужчин в сравнении с женщинами.

Так, мужчины в 1,9 раза чаще оценивали свое здоровье как отличное, в 1,2 раза чаще — как хорошее. Женщины оценивали свое здоровье в 1,3 раза чаще как удовлетворительное, в 5,8 раза — как плохое.

Уровень психоэмоционального стресса у 16,2% мужчин и 22,3% женщин был высоким; у 44,8% мужчин и 46,6% женщин — средним; у 39,0 и 31,1%, соответственно, — низким. Низкий уровень удовлетворенности жизнью в целом отмечался у 7,1% опрошенных; низкий уровень удовлетворенности условиями жизни — у 8,8%; низкий уровень удовлетворения основных жизненных потребностей — у 7,6%. Средний уровень удовлетворенности жизнью в целом имели 29,6% респондентов, условиями жизни — 56,7%, различными сторонами жизни — 39,1%; высокий — у 63,3; 34,5 и 53,4%, соответственно.

Анализ результатов брачно-семейных установок по методике «Ролевые ожидания и притязания в браке» выявил, что у мужчин на первом месте находится выполнение родительских обязанностей, на втором — взаимная моральная и эмоциональная поддержка в семье, на третьем — установка на профессиональную, общественную, деловую активность, на четвертом — значимость внешней привлекательности партнера, на пятом — ожидание совпадения интересов, ценностей и способов досуга.

У женщин на первом месте установка на профессиональную, общественную, деловую активность, на втором — моральная и эмоциональная поддержка в семье, на третьем — выполнение родительских обязанностей, на четвертом — личностная идентификация с супругом, на пятом — внешняя привлекательность партнера, внешнее благополучие, ориентация на социальное мнение.

Установка на интимно-сексуальную сферу брака у мужчин и женщин находится на последнем (шестом) месте. Сознательно недооценивают значение сексуальных отношений в браке 32,2% мужчин и 20,2% женщин.

Общий уровень семейной тревожности у опрошенных женщин значительно выше, чем у мужчин, за счет показателей всех трех субшкал — вины, тревожности и напряженности, что указывает на неуверенность в каком-то важном аспекте семейной жизни, ощущение беспомощности, неспособность вмешаться в ход событий, происходящих в семье.

Математический анализ качества жизни семей

При наличии набора объективных и субъективных характеристик удовлетворенности семейной жизнью в разных аспектах появляется возможность рассчитать интегральные показатели качества жизни и другие комплексные индексы брачно-семейного состояния людей. Обычно это делается путем суммирования баллов разных характеристик без учета или с учетом весовых коэффициентов, отражающих степень варьирования характеристик. Для оценки весов характеристик удобно использовать метод главных компонент — МГК [17], позволяющий линейно преобразовывать исходное пространство связанных характеристик X={xi} в производное пространство независимых показателей Y={yi} — главных компонент (ГК):

• a) y j = Z a j x i , б) x = Z ^ьл У ] , (8) ii

где:

a ij , b ji — весовые коэффициенты;

aij — коэффициент нагрузки (коэффициент корреляции исходных величин и значений ГК), bji — коэффициент счетов (координаты исходных величин в пространстве ГК).

Сумма (8) удовлетворяет соотношению вида (6) при x 0 i = 0, т.е. переменные y j являются независимыми интегральными показателями, через которые выражаются частные характеристики.

При использовании МГК необходимо исходные данные центрировать относительно их средних значений и нормировать по вариации значений. Важно исключить дублирование исходных переменных x i , т.е. выделить группы коррелирующих характеристик. В силу изменчивости полученных в опросах оценок их корреляция не велика, не превышает R= 0,6 для связей переменных x 5 и x 6 (самооценок материального благополучия и социального статуса), x 13 и x 14 (удовлетворенность условиями жизни и удовлетворение жизненных потребностей) и попарно между собой ( x 5 и x 13 и т.д.) при R> 0,4, поэтому все переменные можно рассматривать как независимые величины на уровне значимости p> 0,999. Низкое значение

R согласно (7) указывает на то, что парные связи индивидуальны у каждого респондента. Вместе с тем соотношение ϕ _13,14 = x ₁₃ / x ₁₄ имеет два устойчивых значения, равных примерно 1 и 3, т.е. по этому значению первых интегралов выборка семей подразделяется на 2 самостоятельные группы с разной чувствительностью изменения удовлетворенности условиями жизни к изменению степени удовлетворения жизненных потребностей.

Для количественного анализа использовались рассчитанные значения ГК, взятые с противоположным знаком для того, чтобы первая ГК (ГК1) положительно (aij>0) была связана с ростом благоприятных факторов, характеризующих качество жизни. Основное влияние (aij>0,3) на преобразованную величину ГК1 (y1) оказывают упомянутые самооценки x5 (покупательной способности семьи), x13, x14 (условий жизни и уровня удовлетворения основных жизненных потребностей). Остальные характеристики в основном влияют слабо положительно. Совсем незначительное (aij<-0,03) отрицательное влияние на ГК1 свойственно x4 (увеличение материального неблагополучия с ростом количества детей в семье), x16-18 (родственная и духовная близость). Последовательность ГК по j определяется объемом объясненной дисперсии λj в изменчивости исходных данных X={xi}. Первая ГК объясняет ρ1=25% информации, вторая — ρ2=12% и т.д.

Первые ГК несут основной полезный сигнал q , остальные — формируют шум разного уровня. К «шуму» можно отнести различного рода средовые воздействия, часть из которых выделяется как характеристики социальной среды q 0 , а остальные — рассматриваются как случайные воздействия фона ε . Итоговая интегральная оценка может служить обобщенной характеристикой состояния, от величины которой:

x = q - q0 + ε         (9)

зависят интенсивность и направленность социально-демографических процессов.

Для выявления уровня сигнала и шума сравниваются величины ρj и соответствующие кумулятивные зна-j чения Ρj = ∑ ρk . k=1

На линии зависимости Ρ j ( ρ j ) выделяются группы линейно упорядоченных точек, соответствующих ГК основного сигнала ( I ), его среды ( II ) и фонового шума ( III ). К группе I отнесено ГК1 (25% вариации), ко второй группе — ГК2-5 (38%), остальные ГК6-18 — к фоновому шуму III (37%). Значения q, q 0 и ε вычисляются с учетом весовых соотношений α _j = ρ _j / ρ ₁ :

q=α1y1 = y1, q0 =β∑αjyj,ε=∑αjyj.

j=2

Смысл поправочного коэффици- можно судить по номеру ГК ( j ), кото-ента β будет раскрыт ниже. О роли рому соответствуют наибольшие исходных показателей X i в определе- нагрузки I a y I > 0,3. Среднедушевой нии интегральных характеристик уровень дохода заметно отрицатель-

но влияет на ГК2 ( a ij = -0,88), т.е. является определяющим в формировании социально-экономической среды жизнедеятельности семьи. Положительно на показатели среды воздействует трудовая занятость женщин, ее удовлетворенность работой на уровне ГК2, но отрицательно этот же фактор влияет на ГК3-4 c позитивной корреляцией с ростом доходов и уровня психосоциального стресса. Отмечается преимущественно отрицательное средовое влияние на ГК2-5 качества жилищных условий x 1 : улучшение условий упрощает среду. В соответствии с этими результатами правильно считать показатель q 0 критерием сложности условий жизни семьи, который снижается с ростом материального благополучия и возрастает по мере возникновения источников психоэмоционального напряжения.

Напротив, величина q , равная значениям ГК1 по каждой семье, определяется в основном субъективной самооценкой благополучия (индексы i равны 5,13,14).

Реальная удовлетворенность качеством жизни равна разности самооценки q и сложности q 0 социальноэкономической среды обитания семьи, различием между субъективной оценкой благополучия и объективной характеристикой социальноэкономических условий: q-q 0 . К этому по формуле (9) еще добавляется воздействие удаленного социального фона е.

Показатель фонового, случайного воздействия е, рассматриваемого как информационный шум, собирается из ГК6-18, зависящих от специальных оценок благополучия. Для определения информативности оценок X i удобно использовать сумму вида

I i = Е jg ^{( а} у ), j = 1

где

g ( a ij ) = 1 при |a j | > 0,3, иначе g ( a ij ) = 0.

Небольшая величина I i указывает на роль x i в детерминации первых ГК. В данном случае работают переменные x i с индексами 1, 3, 5, 8,11 и 15. Величина x 15 (семейная тревога) с высоким коэффициентом a ij = -0,81 влияет на ГК9, обеспечивая в основном его значение. Рост тревожности (снижение благополучия) положительно сказывается на увеличении случайных воздействий.

Основные признаки фонового влияния е. качество жилищных условий (тип домохозяйства) (влияние +), удовлетворённость своей работой (-), количество детей в семье (+), самооценка социального статуса (-) и общность семейных интересов (-). Они могут рассматриваться как малоинформативные, но самостоятельные переменные. Менее значимы в этом смысле самооценки состояния здоровья (-), удовлетворенности условиями жизни в регионе (+), местом в социальной иерархии (-), интимносексуальными отношениями (-) и наличия эмоциональной поддержки в семье (+). Влияние переменных X i через коэффициенты a ij на фон е имеет переменный, случайный характер, в отличие от воздействия на q , где a ij в основном положительны, и на q 0 , где сумма a ij (по j ) главным образом отрицательна. Вычитание q — q 0 изменяет q примерно на 8%, а добавление е — еще только на 1%. В пространстве независимых координат ГК результаты анкетирования классифицируются методом вычисления К-средних [17] (рис. 1).

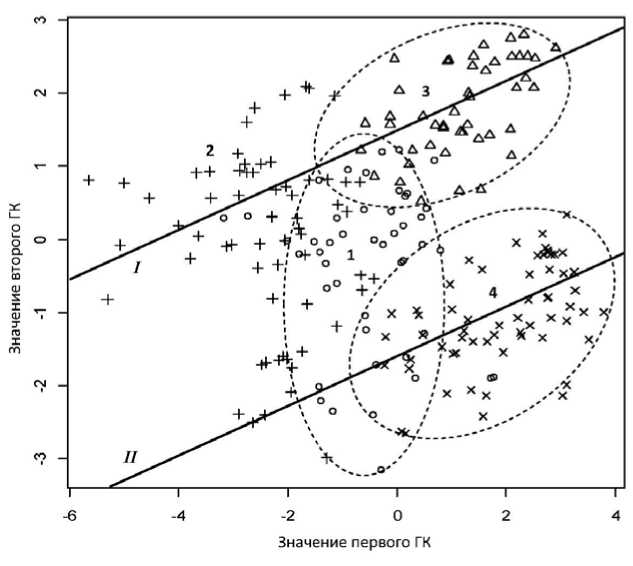
Условные обозначения: линиями показаны две тенденции (I и II) связи значений компонент; эллипсами ограничены объекты подклассов

Рис. 1. Положение объектов наблюдения в пространстве первых компонент ГК1 и ГК2 и их подразделение на подгруппы (1-4).

Сначала семьи статистически делятся на 2 группы с положительными и отрицательными значениями ГК1, т.е. с высокой и низкой оценкой брачно-семейного благосостояния. При делении на 4 группы выделяется подгруппа 1 со средней величиной оценки состояния и группа 2 с низкой оценкой, причем с широким варьированием по условиям среды в значениях ГК2. В группе положительных ГК1 выделяется две подгруппы 3 и 4 двух уровней сложности социальноэкономической среды — соответственно повышенной и пониженной.

Следовательно, при классификации в семьях с низким благосостоянием определяющим является показатель q, а с повышенным благосо- стоянием — факторы среды, обстоятельства жизнедеятельности q0.

На рис. 1 линиями показаны тенденции зависимости ГК2 от ГК1: у 1 =3,1 у 2 — 4,4 (линия I ) и у 1 =3,1 у 2 + 4,8 (линия II ). Это соотношения типа (3б) и (4а), связывающие характеристики системы у 1 = q (уровень благосостояния) и среды у 2 ~ q 0 (сложность условий жизнедеятельности). Значения у 1 — 3,1 у 2 = f 12 = — 4,4 и 4,8 — это инварианты двух тенденций изменения в сложной ( I ) и простой ( II ) средах. Соотношение скоростей изменений v 1 / v 2 =3,1 в обоих случаях примерно одинаковы, и скорости v 1 и v 2 однонаправлены в сторону увеличения показателей у 1 и у 2 или их одновременного уменьшения.

Темпы увеличения благосостояния y 1 в 3,1 раза выше изменения показателей состояния социальноэкономической среды, т.е. среда более консервативна, чем система в этой среде. Появляется возможность при постоянном значении v 1 / v 2 =3,1 провести расчет величины f 12 по каждой анкете. Полученную величину имеет смысл трактовать как инвариант состояния семьи — показатель качества жизни, аналог энергии для социальной системы.

Подобные соотношения можно провести для зависимости q(q0) = eq0+ x для которой в-v 1/v2 =3,3, где коэффициент β в формуле (10) равен соотношению скоростей изменения q=y1 и q0. Характеристика качества жизни х индивидуальна для каждой семьи.

Величиной ε в силу ее относительной малости пренебрегаем. Величина x по разным семьям заметно варьирует вокруг нулевого значения со стандартным отклонением ± 3. Распределения по частоте встречаемости показателей q и x для данной выборки представлено на рис. 2.

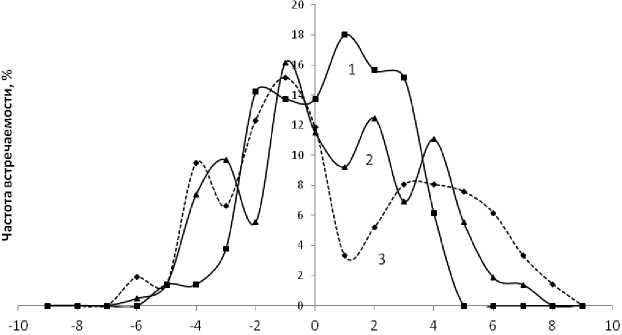
Значение показателя

Условные обозначения: точками обозначены результаты обработки данных, кривыми — тенденции изменения значений .

Рис. 2. Сравнение распределений частоты встречаемости в статистической выборке значений уровня благосостояния семей q (1), состояния среды 3,3 q 0 (2) и качества жизни x (3) .

Величина q распределена почти равномерно со средним значением плотности 15% на интервале значений [-2,3]. Это означает, что в исследуемой выборке семьи с разным уровнем самооценки представлены одинаково часто. Распределение величины q a =3,3 q 0 имеет периодическую структуру с локальными максимумами в значениях этой величины -

• 3, -1, 2, 4, что указывает на дискретность показателя состояния среды в регионе. Распределение по характеристике x указывает на существование двух групп семей с высоким ( x≈ 4) и низким ( х»- 1) качеством жизни.

Однородное распределение по благосостоянию трансформируется неоднородной социально-экономической средой жизнедеятельности семей, что приводит к появлению двух групп семей по качеству жизни и нескольких вариантов подгрупп (см. рис. 1).

Результаты исследования

Расчет показателей q, q 0 , x с использованием МГК и уравнений (8) — (10) рассматривается как вариант кардиналистской оценки состояния сообщества, метод квалиметрической оценки качества жизни по количественным показателям x i . Реализован частный случай уравнения связи (6) с постоянными коэффициентами, определенными коэффициентами нагрузок a ij по каждому признаку x i . Понятно, что в другом регионе (в другой однородной выборке) значения этих коэффициентов будут отличаться, но важно то, что их использование позволяет линейно преобразовывать исходные данные x i в независимые переменные — главные компоненты y j , и выбрать из x i наиболее значимые по степени их влияния на величину ГК в порядке снижения объяснительной способности (информативности) ГК. Основной источник полезных сведений для оценки благосостояния семьи q — первая главная компонента, определяемая самооценкой качества жизни.

Далее выделяются ГК, индицирующие социально-экономическую среду жизнедеятельности q0 и случайный фон влияния, который зависит от воздействия малозначимых признаков. Разность x = q — βq0 как первый интеграл решения дифференциального уравнения (1), с одной стороны, и как линейная функция данных анкетирования xi, с другой, однозначно характеризует устойчивое, сохраняющееся значение каче- ства жизни, индивидуальное для каждой семьи.

Совместное использование двух типов моделей (динамических и ква-лиметрических) позволяет теоретически обосновать правила расчета показателя качества жизни семьи как функцию первого интеграла решения соответствующих дифференциальных уравнений. В модели динамики широкого класса явлений кроме переменных времени и возраста используются различные характеристики состояния социальных систем. С помощью метода главных компонент оценивается благосостояние семьи, определяемое самооценкой качества жизни членов семьи, и вычисляется показатель состояния среды жизнедеятельности (условия жизни), на величину которого в основном воздействуют объективные показатели (доходы семьи, качество жилища и занятость женщин). Влияние остальных данных анкетирования распределено по этим показателям и значениям младших главных компонент, отнесенных к случайному фону.

Обследованные семьи методом вычисления К-средних разделены на две группы по уровню благосостояния и две подгруппы по сложности среды жизнедеятельности. Выделены положительные тенденции связи показателей благосостояния и сложности среды, что позволило оценить отношения скоростей их изменения и по их разности рассчитать критерий качества жизни разных семей как первый интеграл уравнений динамики и квалиметрии, отражающий сохраняющуюся величину благосостояния семьи в конкретной социальной среде. С использованием этих данных построены кривые распределения обследованных семей по качеству жизни, подтверждающие существование двух групп семей с высокими и низкими показателями качества жизни, что, прежде всего, связано с различием объективных условий среды жизнедеятельности.

В теоретическом плане важно обратить внимание на существование альтернативных динамического и квалиметрического подходов к исследованию качества жизни семей, которое является сохраняющимся потенциалом, индивидуальным для каждой семьи. Предложена новая интерпретация результатов расчета по методу главных компонент с выделением показателя благосостояния, сложности среды жизнедеятельности семьи и случайного фонового влияния. Эти результаты будут полезны для развития методов социальной квалиметрии для выяснения интегральных показателей состояния общественных групп и среды их жизнедеятельности.