Динамические модели управляющих нагрузок реологических систем

Введение. Для моделирования поведения сложных динамических систем необходимо вводить соответствующие сложные функции безразмерных параметров, отражающих весь комплекс действующих на объект нагрузок. Чтобы получить такие зависимости, целесообразно использовать методы масштабного моделирования, подробно описанные в литературе [1].

Постановка задачи. В качестве управляющей нагрузки удобно рассмотреть функцию гармонического изменения действующих напряжений а( t ), в качестве управляемой функции отклика системы – соответствующую ей функцию деформаций, также изменяющуюся по гармоническому закону с запаздыванием по фазе, равным углу механических потерь Аф.

Моделирование поведения реологической среды. Универсальной моделью поведения реологической среды являются наследственные уравнения типа Больцмана и Вольтерра для полимерных композитных материалов и подобных им реологических сред. Однако наиболее наглядно поведение систем при данных условиях можно описать с помощью динамических моделей вязкоупругости на основе трехпараметрического дифференциального операторного уравнения.

Примем закон гармонического нагружения реологического тела в виде функции:

е + 2 - е + 4 п ² f ²£ = ^ ( t ) ,                                   (1)

П где ^(t) - функция внешней нагрузки; е - деформация тела; Е/п - коэффициент затухания (отношение модуля упругости к коэффициенту вязкости); f0 - собственная частота и период незатухающих колебаний.

Функцию внешнего воздействия в правой части уравнения (1) можно представить множеством способов, исходя из удобства рассмотрения задачи. В любом случае функция ^ ( t ) – это произведение:

^ ( t ) = KN ,                                     (2)

где N – параметр нагрузки; Κ – константы, характеризующие объект воздействия нагрузки.

Наиболее удобными можно считать следующие способы выражения функции ^ ( t ) , используя основные положения теории размерностей [1]:

^ ( t ) = D- а ( t ) = Em	D -/A -----^( t ) = EV p	D -^ D -^ -------o ( t ) = t p o ( t ) ; Xn V p     n V p	(3)
^ ( t ) = TE-p ( t ) = Dmtp	E -< A p ( t ) DV P t p	E   „, .    E X -.. = nTZt p ( t ) = nv p ( t ) ; DV p tp     DV p	(4)
^ ( t ) = ' W ( t ) = Sm	—W ( t ) = SV p	-- ^Q Q ( t ) = -—- a S ( t ) ; SV p     a SV p	(5)

—         —           — ^ ( t ) = V A T ( t ) = v A T ( t ) = ^- A T ( t ) ; Sm      S      SV р	(6)
^^                     ^^ T ( t ) = — A T ( t ) = ^ m A T ( t ) = — A T ( t ) = —A T ( t ) ;	(7)
Sm      S      Sm      S Vр
^^                          ^^                          ^^ —              —               — T ( t ) = — Т — A T ( t ) = — Т — A T ( t ) = — Т— t p A T ( t ) ;	(8)
А ESm      А ESV р      Ап Sm
^ ( t ) = Л P ( t ) =       p ( t ) = -tp- P ( t ) = —1— P ( t ) ;	(9)
ESm     ESV р      SV р     А SV р
—      t —         —         — * ( t ) = V D ( t ) = -f — ( t ) = -5- D ( t ) = — D ( t ) ; S      S      ES       А S	(10)
/ X D •        D •         D •        D • ^ ( t ) = 1 o ( t ) =----- 1 o ( t ) =------- o ( t ) =----- 1 o ( t ) ; w Em p     EV р p    А EV р      EV р p	(11)
\ D —       D —       D п — z x ^ ( t ) =----- 1 o ( t ) =------ 1 o ( t ) =   —o ( t ) . v ’ АEm p      А EV р p      А E 2 V р	(12)

В соотношениях (3)-(12) введены следующие обозначения: D – жесткость тела;

^{—                                  —}                                              —

D - поглощенная доза излучения; D - мощность поглощенной дозы излучения; о(t) - нагрузка, выраженная через напряжения; p(t) - нагрузка, выраженная через механический импульс; W(t), Q(t) - соответственно механическая энергия и тепловая; AT(t) - изменение температуры при нагреве тела; Р(t) - мощность механического воздействия; S, AS(t) - энтропия и изменение энтропии; С, cm - темплоемкости соответственно атомная и массовая; а, АТ - тепловое расширение и теплопроводность; S, V, р, m - площадь, объем, плотность и масса тела; А, tp - эмпирическая константа и время релаксации; d(t), d(t) - первая и вторая производные от действующей нагрузки; п - коэффициент вязкости.

Функцию нагрузки ^(t) можно определить также с помощью операторного уравнения: ^(t) = Р0^ + М + P2^ = K(p)о(t).(13)

Преобразуем общую форму записи операторного уравнения к виду, соответствующему уравнению (1), используя коэффициенты:

p2*(Г + 2ЕР*<3 + 4п2 f *2p*о = ^(t).(14)

п

Выразим искомые коэффициенты через вспомогательные величины:

p2 = p2* ,

Тогда:

p i = 2 ^Ep * ,                                     (16)

п pо = 4n2 f о2p0 .                                        (17)

*    D п	(18)
P 2    р 2 т 7-2    , А E m Е * D
P i = 2 P i = х      , п    А Em	(19)

*    Dn р1 = Г 2 , 2XE m

D

P о = ^{4 n} fзР о = — , Em

* D

P ° = F--- 2 . Em to ₀

Подставим полученные коэффициенты в (14):

D η

X E ² m

••

D

σ+ λ Em

S + -^-S = V ( t ) .

Em

Полученное уравнение показывает, что приведения ее к наиболее компактному виду удобно использовать в качестве функции нагрузки первое выражение в (3).

Выполним подстановку и преобразования уравнения (23):

Е . X Е    X Е „, .

a +—a +-- a = --a ( t )

ηηη или a + XS \Xa=Xa (t).

Выразим функцию нагружения через параметры системы, соответствующие левой части уравнения (25), и уравнения для функции напряжений и ее производных, получим:

a = pX2a0e-Xt.(26)

Упростим выражение:

(1 - e ^X t ) =

1 в^е^-X t

S ⁽ t ) ,

согласно которому определим:

a ( t ) = ра _ое ^-X t (1 - e ^X t ) .                                            (28)

Полученное уравнение характеризует релаксацию нагрузки после ее установления. В случае, когда нагрузка изменяется по некоторому временному закону, полное выражение функции нагружения примет вид:

V ( t ) = s ( t ) -pa ° e ^-X t (1 - e ^X t ) .                                    (29)

Такой вид функции нагружения наиболее компактен и удобен для анализа вязкоупругой среды. В большинстве случаев нагрузка V(t) изменяется по гармоническому закону. Обо- значим максимальное значение возмущающей силы Ψm , тогда, при гармоническом законе изменения и в соответствии с условиями (3), можем записать:

D

£ + 2 X£ + to_n£ = V --- cos to t                           (30)

о m

Em или в другом виде:

Е ω

Е + 2 — E + to o E = V m —^о cos to t , η          λη

~ где to = 2nf = 2n/T - угловая частота возмущающей силы и установившихся колебаний систе-~ мы; f, T - частота и период нагружения.

Решением уравнений вида (30)-(31) является уравнение [2]: е = V _m cos( to t - a ) ,

где a - фазовый сдвиг резонатора (реологического тела) относительно возмущающей силы,

_             гор               2 to8             2 toX

a = arctg— 7—---- .. = arctg ,---- у = arctg—----- .

m ( ^to 0 ^to ) ^to 0 ^-to           D - _to 2

m

Таким образом, если нагрузка выражается через напряжения тела, то запаздывание колебаний составляет определенную выше величину угла механических потерь Аф , причем в большой степени зависящую от частоты вынуждающей силы to и коэффициента затухания

Е 1

в = 8 = X = - = —, t >  0 .

П t p

Следовательно, в данном случае a = Аф . Тогда [3]:

a = Аф = arctg — = arctg Д0.(34)

-S

Преобразуя уравнения (33) и (28), получаем:

Аф = arctg /2®E 2\ = arctgE-(1 -eхt) = arctg—(1 -eXt).(35)

^n(to o ^—to)         X t p                   t p

Согласно теории колебаний [2], амплитуда колебаний реологического тела изменяется от частоты возмущающей силы to и коэффициента вязкого трения р :

Y m ^{( Д )} = ^— m m ( ^to 0 ^-to 2 ) ^+в 2 ^to 2 ²

или

Y m ( д ) = -m m

(^to 0

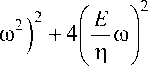
Запишем это выражение с учетом эмпирического коэффициента:

Y m ( д ) = -m ( to 2 m ^x

-to ² ) + 4 X ² to ²

~

Анализ уравнений (36), (37) показывает, что при to ^ to0 и при в > 0 амплитуда мо- жет превысить допустимые для реологического тела значения, определяющие прочность тела. Динамические условия разрушения можно получить из условий прочности. При заданной возмущающей силе — (t) и коэффициенте вязкого трения р амплитуда Ym (0 - 282 .                       (39)

2 m ²

Используя эмпирические константы и выражения связи с вязкоупругими характеристи- ками полимерных материалов, получаем:

^to pe3

^to 0 - ²^г=7 ^to 0 ^{- 2 х} 2 п

D 2 m t ² p

Параметром вязкого трения является коэффициент затухания 5 . При малых значениях 5 величина Y m ( 6 ) резко возрастает. Уравнения (36)-(38) справедливы и для случая статического нагружения тела при условии Т m ( ю = 0) .

Чтобы найти выражение для резонансной амплитуды, подставим (40) в (36)-(38):

1 Т m Ю2 в 2 2_^ m_ ^ m , Y m И - в ( '" - 4 m 2 ) = вю - 2 m 8ю rm- Т ml m2 12 Г1- Т m ( D £ ' 1- Y m ( б ) - П Т ( Ю 0 Х ) 2 - в               в ( m п 2 ) . Т    Т    Т п Y ,( 6 )   m-  m-   m -L . 2 m Хю 2 m 5to 2 mE ю

(41) (42) (43)

Величина угла механических потерь Аф характеризует основные свойства реологического тела, материала или системы, а ее выражения (34)-(35) позволяют получить обобщенную связь между характеристиками тела и параметрами нагрузки.

Выводы. Полученная динамическая модель вязкоупругого материала, конструкции или системы при управляющем воздействии нагрузки, действующей по заданному закону в течение некоторого времени, позволяет осуществить эффективный анализ поведения реологического тела в целях оценки изменения его напряженно-деформированного состояния.