Динамические особенности функционирования рабочей клети автоматического стана трубопрокатного агрегата

Условия эксплуатации отечественных трубопрокатных агрегатов (ТПА) влечет за собой ужесточение режимов функционирования основного и вспомогательного оборудования технологической линии. Автоматический стан, согласно циклограмме работы ТПА формирующий начальные параметры изделия в технологическом процессе производства бесшовных горячекатаных труб, является наиболее узким местом [1]. Прокатка гильзы на автоматическом стане ТПА характеризуется тем, что на гильзу, взаимодействующую с валками и оправкой, воздействует стержневой механизм ее удержания на оси прокатки. Следует отметить, что данные условия формируют специфические начальные условия технологического процесса, обуславливают сложное поведение рабочей клети и в результате этого – нестационарные динамические процессы на самом автоматическом стане ТПА [2].

Анализ источников

Наименее изученными среди динамических процессов, сопровождающих процесс прокатки гильз на автоматическом стане, являются поведение станины рабочей клети со всеми механизмами ее удержания. Особенно- приводящие к заметным искажениям очагов деформации. Следовательно, для обеспечения устойчивой геометрии гильз, прокатываемых на автоматических станах ТПА, кроме всего, существенное практическое значение имеет решение задачи обеспечения стабилизации состояния рабочих клетей.

Цель работы

Определение реальных спектров и уровней динамических нагрузок позволило бы разработать рекомендации по совершенствованию рабочих клетей автоматических станов ТПА, расширить их технологические возможности, повысить долговечность и надежность функционирования.

Метод решения задачи

Данная работа выполнена на основе развития математической модели динамических процессов в механической системе автоматического стана ТПА, где реализованы определенные шаги по установлению параметров функционирования рабочей клети с прокатываемой гильзой в постановке фундаментальных задач динамики. Предложенный подход более корректен и удобен при изучении сложных динамических явлений в элементах автоматического стана ТПА. Ниже в работе приведены результаты исследования динамики рабочей клети автоматического стана ТПА 350 путем развития принятых расчетных схем и математической модели исходной механической системы [4, 5].

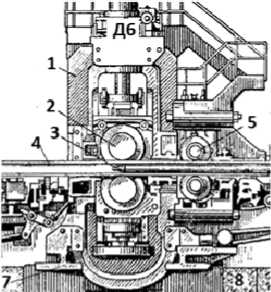
Автоматический стан ТПА 350 и одна из схем размещения датчиков, информирующих о пространственных перемещениях различных участков рабочей клети, представлены на рис. 1.

сти в з аимоде й с тв ия г ил ьзы с ра б оче й к ле т ь ю ав т ома ти чес к ого с т а н а су щ е с тв е н н о в ли яю т н а ха рак те р фу н к ц и они ров а н и я д анн ой ме х ан и че ск ой с и с т е мы. Оп ыт и с с ле д ова н и я у с л ов и й э к с п л уа таци и Т ПА с автома ти че ск и ми ста н а ми п ок аз ы в а е т, чт о и х отли чи тельной о с об е н н о с тью от д ру ги х с та н ов те хн о логи ч еск ого ц ик ла п рока тк и тр уб я в л я етс я нали чи е н ес та ц и он а рных д и н а м и че с к и х п роце с с ов. При э том д и н а ми че с к и е нагрузк и , н а п ри ме р н а а в том атическ ом с та н е Т ПА 35 0, в пе ри оды захвата гильзы в 3– 5 раз а превосход ят на грузки п ри у с та н ов и в ш е мс я п роц е с се прока тк и . М а те ма ти чес ка я мод ель п роц е с с а в за и мод ействи я п рок а ты ваем ой з а готов к и с рабоче й кле ть ю , п ре длож е н н а я в ра б ота х [ 3, 4] , н е п озв оляе т п олн ос тью п редс та в и ть ос об е н н о с ти ф ун к ц и он и ров а н и я ра б оч е й к л е ти в п роц ес се прока тк и гил ьзы. Од н ак о а н а ли з ма те ма ти ч еск ой моде ли н е с т а ц и он а р н ого в за и моде й с тв и я п рок атыв ае мого ме тал ла с р а б оче й к л е ть ю ста н а , ра сс мотре н н ой в ра б оте [3] , п озв олил п ол учи ть возможн ос ть описа ть форми ров а н ие н агрузок в п е ри оды п е рех од н ых п роце сс ов .

Среди сов ок у п н ос ти на гру зок , де й с тв у ю щих н а ра б очу ю к леть и д ру ги е б а зов ые э л е ме н ты а в тома ти че ск о го с та н а Т ПА, н аименее н е и зу че н н ыми являю тс я зн а чи те льн ы е п о вели чи н е и и зме н яю щ и е с я в о в ре ме н и н еста ц и онарн ые д и н а ми че ск и е н а гру зк и . Мн ог очисле н ные и с сле дов а ни я у с ловий эксплуатац ии а в том ат и чес ких с т а н ов Т ПА п о к а за ли, ч т о п ри з ахвате ги льз в а лк а ми ра бочи е к л е ти сов е рш аю т н е кон троли р у е мые д в и же н и я в п ростра н с тв е , что о к а з ыв а е т с у щ е с тв е н н о е влияние на напряженно- де форми ров а н н ое сос тоян ие э ле ме н тов к ле те й , ф орми ру е т сложн ы е к а рти ны п роц ес с ов п ро к а тк и ги льз ,

а)

б)

Рис. 1. Автоматический стан ТПА (а) и схема размещения датчиков на полустанинах рабочей клети ТПА 350 (б). 1 – станина клети стана; 2 – рабочие валки; 3 – оправка со стержнем; 4 – гильза (трубная заготовка); 5 – ролики обратной подачи; 7, 8 – узлы удержания рабочей клети

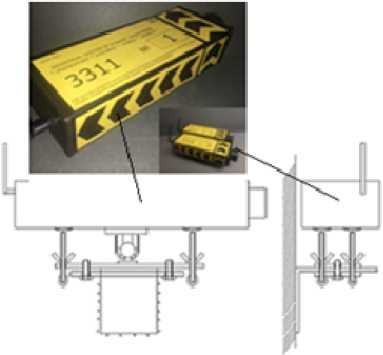
Фиксация л и н е й н ых и у г лов ых с м е ще н и й у ча стк ов раб оче й к ле ти ос у щ е с тв ляла с ь уни в ерс а льными д а тчи ка ми п рос тра н с тв е н н о го ориентирования, о с н овны м чув с тв и те ль ны м э л е ме н том к оторы х явл яе тс я д и н а ми че с к ий и н к л ин оме три че ск и й мо д у ль DCA126-T, раз р а б ота н ный ш в е й ц а р с к о й к омп а н и е й OEM и производимый компанией RI O N Technology (Г онк онг) [ 7] . Н а ри с . 2 пре д с та в л е н ы универ са льн ы е да тчи к и п р ос тран с тв е н н ого ориенти р овани я и п ол ученн ы е в ре зу льта те об раб отки и н форма ц и и да тчи к ов ка рти н ы п рос тр а н с т в енн ы х п е ре мещ е н и й ра зли чн ых у ча с тк ов клети во время прокатки гильз.

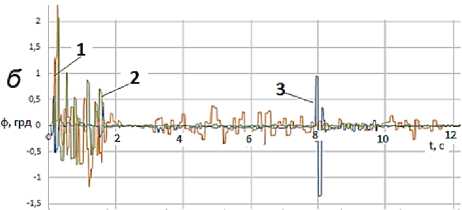
На р ис. 3 пред ст ав лен ы л инейн ы е и у г ло вые с м е щения станин ы раб о ч ей клет и а втоматического стана ТПА 3 5 0 п р и п р о к атк е трубы 273 х 6,3, по л уч е нны е по п ок аз аниям датчика Д6.

Интенсивность нестационарного воздействия со стороны очага деформации на рабочую клеть, изменение во времени инертности трубы и параметров жесткости крепления ра- бочей клети к опорным плоскостям значительно усложняют описание динамических процессов на автоматическом стане ТПА. Отметим, что исследование развитой динамической модели «рабочая клеть – механизм удержания клети» позволит проанализировать динамическое состояние как элементов рабочей клети, так и взаимосвязанных узлов механической системы в течение всего процесса прокатки гильзы. Актуальным становится установление взаимосвязи между динамическими процессами, например на автоматическом стане ТПА 350, и параметрами разностенно-сти прокатываемых гильз. На основании полученного следует разработать ряд мероприятий и предложений по комплексной модернизации рабочей клети и оборудования выходной стороны, например автоматического стана ТПА 350. Для формирования научнообоснованных предложений по совершенствованию конструкции рабочей клети автоматического стана ТПА необходимо более глубоко изучить влияние различных параметров и

а)

б)

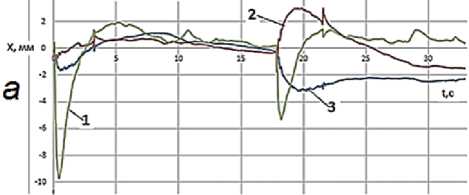
Рис. 3. Линейные (а) и угловые (б) смещения рабочей клети автоматического стана ТПА 350 при прокатке трубы 273 х 6,3 (показания датчика № 6): 1 - линейные и угловые смещения датчика относительно вертикали; 2 – линейные и угловые смещения датчика относительно оси прокатки; 3 – линейные и угловые смещения датчика относительно оси, параллельной начальному положению осей валков

Рис. 2. Универсальные датчики пространственного ориентирования (а) и полученные в результате обработки информации датчиков картины пространственных перемещений различных участков клети во время прокатки гильз (б)

особенностей формирования технологического процесса прокатки гильз на динамику всей механической системы стана и качество готовой продукции. Выбранное направление исследований отличается от известных [1–5] подходом к анализу и синтезу взаимосвязанных динамических процессов с учетом податливости опорных узлов механизма удержания станины на опорных шинах и циклически изменяющихся технологических нагрузок, действующих со стороны очага деформации на элементы рабочей клети.

Для установления взаимосвязи динамики рабочей клети с условиями функционирования автоматического стана ТПА переходим к описанию математической модели динамических процессов. Математическую модель исходной механической системы рабочей клети автоматического стана ТПА в наиболее общем виде представляем с помощью дифференциальных уравнений, описывающих поведение выбранной расчетной схемы (рис. 4).

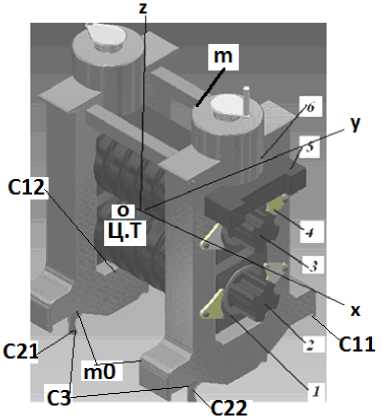
Рис. 4. Расчетная схема рабочей клети автоматического стана ТПА

Далее переходим к анализу выбранной динамической модели рабочей клети автоматического стана ТПА с восемью степенями свободы и решению многофакторной задачи.

Выбираем пространственную систему координат в центре масс рабочей клети и преобразуем исходную сложную динамическую модель механической системы с использованием методик [3, 5, 6] в упрощенную механическую систему жестких тел, определенным образом связанных между собой в опорных узлах упругими элементами. Простран- ственное положение данной механической системы в процессе колебаний характеризу- ется соответствующими координатами в выбранной системе отсчета. Исходя из выбранной расчетной схемы рабочей клети стана (см. рис. 4) определяем кинетическую и потенциальную энергии механической системы соответственно. С учетом определенных начальных и граничных условий поставленную задачу представляем в постановке традиционной задачи динамики механической системы [7–14].

Считая лапы станины и тумбы (шины), удерживающие рабочую клеть на опорных механизмах, деформируемыми, для упрощенной механической системы с четырьмя степенями свободы кинетическую и потенциаль- ную энергии системы находим в виде:

1   222      22

T = 2 m ( ^z11 ⁺ i ^ф 16 ) ^{+ 2 m}0 ( ^z 12 ^{+ z} 13 ) ⁺

⁺ 2 m ( ^Z 21 + i ^ф 26 ) + ² m 0 ( z 22 ^{+ z} 23 ) ;

1                      21

П = ²2 с и ( z ii ⁺ a Ф 16 ) ^{+ 2}2 ^ci2 ( z ii - b Ф 16 )

+

⁺ 2 2 c 3 ^{( z} 12 ^{+ z} 13 ) ⁺ 2 2 ^с 21 ^{( z} 21 ⁺ c ^ф 26 ) ⁺

1                       21

+ 2 2C22 (z21 - dф26 ) + 2 2c3 (z22 + z23 ) , где m – масса рабочей клети автоматического стана; m0 – масса опорного узла рабочей кле- ти автоматического стана; с11, с12, с21 и с22 – приведенные жесткости соответственно передней и задней частей опорных узлов рабочей клети стана; с3 – приведенная жесткость тумб (шин) механизма удержания рабочей клети; z11, z12 – динамические перемещения центра масс рабочей клети автоматического стана в плоскости z–y; z21 , z22 – динамические перемещения передней части рабочей клети автоматического стана в плоскости z–x; z13, z23 – динамические перемещения опорных узлов (шин или тумб) рабочей клети автоматического стана в вертикальной плоскости; Ф16, ф26 - угловые перемещения станины рабочей клети стана вокруг осей x и y ; a , b , с, d – параметры расположения центра масс рабочей клети в выбранной системе отчета; е – расстояние от оси x до точки приложения технологической нагрузки P(t) со стороны прокатываемой гильзы. Из [5] известно, что технологическая нагрузка, действующая со стороны очага деформации на валки рабочей клети, носит гармонический характер:

P ( t ) = P 0 + P 1 sin ( to t ) .

Здесь P ₀ – статическая составляющая силы прокатки трубы, а P ₁ – амплитудное значение данной силы. Отметим, что гармоническая составляющая силы прокатки гильзы имеет соответствующую частоту to в силу винтовой разностенности гильзы после прошивного стана.

Используя уравнения Лагранжа, составляем дифференциальные уравнения движения рабочей клети автоматического стана ТПА. В очередном приближении для принятой динамической модели механической системы с четырьмя степенями свободы в постановке базовой задачи Коши запишем:

m d zd? t ) ^{+ 2 Сп} ( ^{Z n (} t ) - z i2⁽ t ) ⁺ a ^ф 1б⁽ t ) ) ^{+ 2 c} i2 ( ^{Z n (} t ) - z i2⁽ t ) - b ^ф 1б⁽ t ) ) = 0;

Z 11 (0) = 0,01;   dz^ = 0;

dt

² m ° d Z 12⁽ t ) ^{+ 2 C n} ( ^{Z n (} t ) - ^z 12⁽ t ) ⁺ a Ф 16⁽ t ) ) ^{+ 2 c} з ^z 13⁽ t ) = 0;

Z 12 (0) = 0;   dz ^ = 0;

dt

² m 0 ^d      t ) ^{+ 2 C} 12 ( ^z 11⁽ t ) - ^z 12 ⁽ t ) - b Ф 16 ⁽ t ) ) ^{+ 2} c 3 ^z 13 ⁽ t ) = 0;

dt ²

Z 13 (0) = 0;    dz !⁰⁰ ) = 0;

dt mz12 d Ф1б( t)+2 C11 a (Zn (t) - z12(t)+a Ф16(t)) -2 C12 b (z11(t) - z12(t) - b Ф16(t))=(P0+P1sin(to t)) e;

Ф 1 ₆ (0) = 0,015;   d^⁰)- = 0.

dt m d z22 (t) + 2C21 ( z21(t) - z22 (t) + Cф26 (t) ) + 2C22 (z21('- - z22('- - dФ26 ('- ) = 0

z 21 (0) = 0,01;   dz²^ = 0;

dt

• ² m 0 ^d zd 22 ⁽ t ) ^{+ 2 C} 21 ( z 21⁽ t ) - z 22 ⁽ t ) ⁺ c Ф 26 ⁽ t ) ) ^{+ 2} c 3 z 23 ⁽ t ) ⁼ ^

z 22 (0) = 0;   dz ² ^^ = 0;

dt

• ^{2 m} 0 ^d- z ²3^^{t )} + ^{2 C} 22 ( z 21⁽ t ) - z 22⁽ t ) - d Ф 26⁽ t ) ) + ^{2 c} 3 ^z 23⁽ t ) = 0

dt ²

• z 23 (0) = 0;   dz^f¹ = 0;

dt mi22 ^"Ф2^ + 2C21 c(z21(t) - z22(t) + cФ26(t)) - 2C22d(z21(t) - z22(t) - dФ26(t)) = 0

Ф2б(0) = 0,015;  d^^0- = 0, dt где i1 – радиус инерции рабочей клети относительно оси x ; i2 – радиус инерции рабочей клети относительно оси y .

пустимый уровень виброактивности механической системы.

Для получения объективной картины изменения качественных характеристик прокатываемых труб до и после восстановления (ремонта) клети автоматического стана ТПА 350 и была произведена оценка данных тол-щинометрии труб, прокатанных в разное время (до и после ремонта механизма удержания рабочей клети соответственно).

На рис. 6 приведена картина изменения разностенности по длине партии черновых труб, прокатанных на автоматическом стане ТПА 350 [7]. Результаты исследования раз-ностенности прокатываемых труб указывают на правомерность принятых решений по модернизации опорных узлов механизма удержания рабочей клети автоматического стана ТПА 350.

Известно, что в ходе реализации технологического процесса высокая динамичность системы «рабочая клеть автоматического стана ТПА – механизм её удержания» обуславливает формирование повышенной разно-

Далее решение системы дифференциальных уравнений (3) реализуем численно методом Рунге – Кутта в среде программного продукта Mathcad, для наиболее распространенной первой формы колебаний механической системы «рабочая клеть – механизм удержания клети».

Динамические особенности функционирования рабочей клети автоматического стана ТПА 350 с учетом принципа суперпозиции линейных и угловых перемещений механической системы представлены на рис. 5.

Сопоставление результатов численного расчета (см. рис. 5) и экспериментальных исследований (см. рис. 3) показывает, что дифференциальные уравнения (3) с достаточно высокой степенью точности описывают вынужденные колебания рабочей клети на опорных механизмах автоматического стана ТПА 350. Амплитудно-частотные характеристики динамических процессов при колебаниях рабочей клети за время реализации всего технологического процесса прокатки гильзы на автоматическом стане ТПА 350 превышают до-

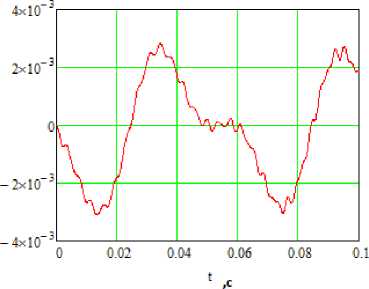
Рис. 5. Динамика рабочей клети автоматического стана ТПА 350 (прокатка черновой трубы диаметром 273 х 6,3 мм, материал - сталь 20): z 1 ( t ) - суммарные линейные смещения центра масс рабочей клети на опорах; z ₂( t ) - суммарные линейные смещения передних лап рабочей клети на опорах; z ₃( t ) - суммарные линейные смещения задних лап рабочей клети на опорах; ф ₆( t ) - суммарные угловые перемещения рабочей клети стана

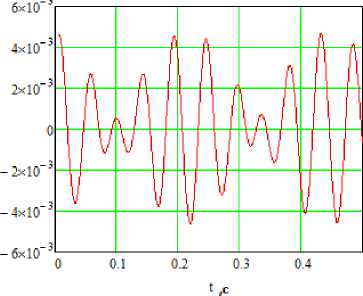
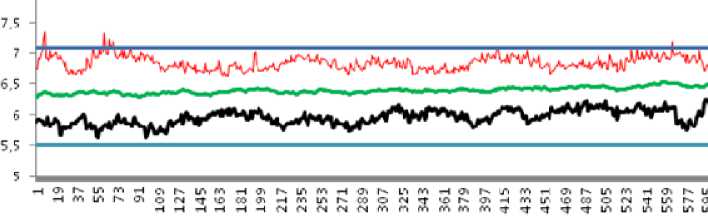
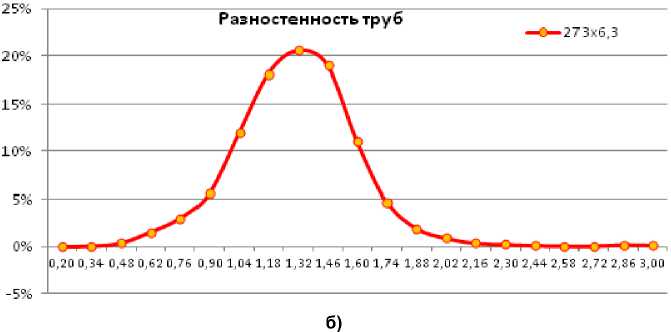
Рис. 6. Результаты стенкометрии автоматического стана ТПА 350 (а) и распределение продольной разностенности труб (б) размером 273х6,3 мм после ремонта механизма удержания рабочей клети

сте н н ос ти гильзы [ 15] . На п ос лед у ю щ и х у ча стк а х в оз де й с тв и я на об р а б а тыв ае мое и з д е лие п роц е сс н ос и т с л ожный и тру д н о у с тра н и мый характер. О чеви д н о, что у че т д и н а мики рабо ч е й к ле ти и и н те н с и в н ос ти в озд е й с тв и я с о сторон ы очага де фо рма ц и и с тана яв ляется определяющим параметром д ля рассматриваемой модели. Следует от ме ти ть, что возможность м ате ма ти чес к о го моде ли ров а н ия различных р е ж и м ов п рока тк и гиль з ы на э та пе п роек тиров а н и я те хнол оги че ск и х процесс ов п рок атк и т руб н а а в томати че с к ом с т а н е Т ПА суще с тв е н н о отли ча е т полу че н н ые ре зу льта ты от ре зу льта тов ра не е и зв е с тн ых ра б от в о б ла с ти и с с л е д ов а н и я ди н а ми к и и в и б ро а ктивности упругих подс и сте м ра б оч е й к л е ти и меха н изма ее у д е р жа н ия н а оп орн ых у зла х стана [10–14].

Выводы

Уточнена расчетная схема взаимосвязанных механических подсистем рабочей клети автоматического стана ТПА и разработана математическая модель динамики для механической системы «рабочая клеть – механизм удержания клети» для механической системы с четырьмя степенями свободы. Учтены цик- лический характер технологических нагрузок и динамические характеристики базовых элементов (шин, тумб и анкеров) механизма удержания рабочей клети автоматического стана ТПА на соответствующих опорных плоскостях. Приведены результаты численного решения дифференциальных уравнений перемещений узловых элементов рабочей клети автоматического стана ТПА. Это позволило в комплексе оценить амплитудночастотные характеристики как рабочей клети, так и подсистем опорных узлов клети автоматического стана.