Динамические особенности процесса трения в ультразвуковом резьбовом контакте

Кулеш Ирина Михайловна, аспирантка кавитационные полости в среде СОЖ. Знакопеременный характер давлений в таких плоскостях приводит к образованию кавитационных пузырьков и их схлопыванию, что может создавать ударные гидродинамические волны с давлением до 100 МПа [2]. Интенсивные акустические течения улучшают смазывающе-проникающую способность СОЖ и снижают силы трения. Указанные возможности ультразвука позволяют надеяться на положительный эффект при различных технологических процессах, в том числе и при сборке резьбовых соединений с резьбообразующими крепежными деталями.

С другой стороны, снижение сил трения в нестационарных процессах связывают с проявлением «скоростной» зависимости коэффициента трения [3]

л f f (V) = -fr

• ¹ + а V , (1)

где f 0 – коэффициент трения покоя; a – константа; V - переменная скорость относительного скольжения.

В условиях УЗК относительная скорость скольжения всегда выше стационарной. Тогда, в соответствии с данными работы [4], коэффициент трения в определенном диапазоне скоростей имеет тенденцию к понижению, в силу соотношения

• f_ = T 0- = I f ² - B—A ®

• ^JB N V V ² + A ² ® ² , (2)

где T 0 – единичная тангенциальная сила сопротивления без вибраций; N – нормально действующая сила; f 0 – стационарный коэффициент трения; B – коэффициент; А – амплитуда УЗК; V - стационарная скорость; ® - круговая частота вибраций.

Уточненная характеристика трения представляется в виде суммы характеристик сухого и (линейного и нелинейного) вязкого трения [6]

F = N ( f i signx - f 2 x + f 3 x ³)

где N – нормальная реакция; f 1 , f 2 , f 3 – постоянные коэффициенты соответственно сухого, линейного и нелинейного вязкого трения.

В данном уравнении члены, пропорциональные скорости Х ( t ) представляют собой первые члены разложения гладкой функции вязкого трения в ряд Маклорена. Такая характеристика называется разрывной характеристикой некулонова трения, которая при некотором значении положительного или отрицательного направления скорости проходит через минимум характеристики. Во всех трех формулах (1, 2, 3) наблюдается снижение сил трения при росте колебательной скорости. Для определения условий трения в резьбовом витке, совершающем ультразвуковые колебания, рассмотрим работу резьбового витка, представленного кольцом, на которое с двух сторон действуют элементарные тела n , сжимая кольцо. Тела n имитируют охватывающие витки корпуса в плотном резьбовом контакте (рис. 1).

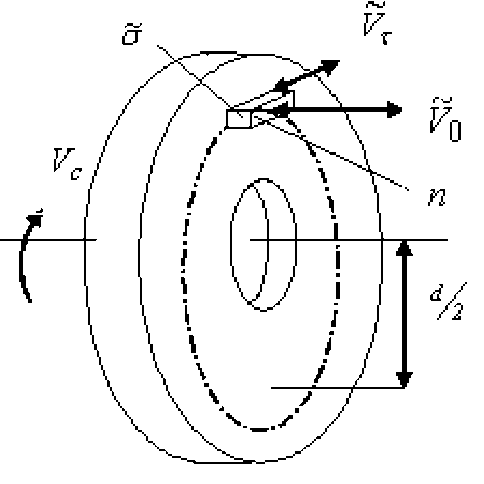
Рис. 1. Модель резьбового соединения

На поверхности его начинают действовать давления (~ . Кольцо вращается со скоростью, тангенциальный вектор которой представлен величиной V c . В случае прикладывания к телам n ультразвуковых колебаний, тела

~ могут передавать кольцу осевые V0 и тангенциальные VT колебания, изменяя стационарный режим его вращения. Диаметр, на котором тела n прижимаются к кольцу, равен d. В стационарном режиме крутящий момент, необходимый для преодоления сил трения равен

M = 2 о- F k ■ fd

, где Fk – односторонняя площадь контакта; f – коэффициент трения.

При наличии обоих векторов УЗК, осе-~~ вых V0 и тангенциальных VT, суммарная скорость скольжения элементарной точки боковой поверхности контакта будет формироваться следующим образом. При условии, что Vc > V, где V = ~2 + V2 , суммарная скорость скольжения будет определять направленность вектора VT относительно Vc. Рассмотрим этот механизм на рис. 2. Если результирующая амплитуда УЗК подчиняется закону

x = As • sin tot

где A ₂ - амплитуда; to - круговая частота колебаний, то колебательная скорость будет подчиняться закону

1^*

Хе = V = AЕ • to-costoT,

обретая максимум при величине V % max = 2 П- f • A ^ = 2 n- f.A + A T , где А о и А т – амплитуды соответствующих направлений УЗК. Тогда результирующая скорость скольжения будет равна

~~

V ^ = V c + V • cos to t

Рассмотрим виток как элементарную массу в колебательной системе. Отбросив медленную компоненту, связанную со скоростью V c , представим, что виток находится под действием быстрых осевых ( А о ) и тангенциальных ( А τ ) УЗК. Тогда его поведение можно описать следующей системой дифференциальных уравнений

mХ + cx = Q • sin to t

~

где m – масса витка; c – жесткость упругого реологического контакта поверхностей витка и тела n ; x - осевая координата; S - коэффициент вязкого сопротивления; Q - возмущающая

осевая сила; J – момент инерции витка; φ – круговая координата; M~ - возмущающий крутящий момент.

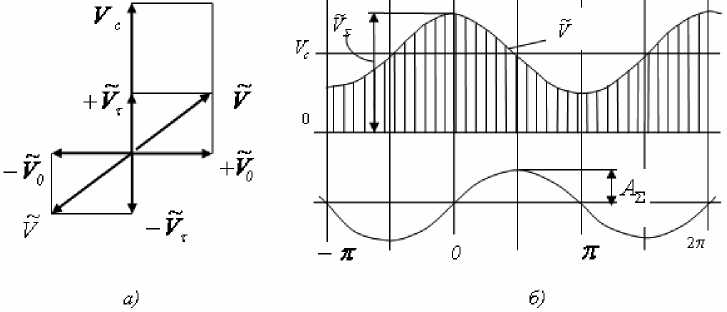
Рис. 2. Формирование суммарной скорости скольжения: а) векторная схема; б) форма колебательного процесса

Для получения возмущающей силы возьмем значение интенсивности УЗК:

Q = J • F_k = ^Cy" to A² F_k

V k    ^k      2V k          ^k ,        (6)

где ρ – плотность материала; C y – скорость ультразвука в материале. Подставив в формулу ( 6 ) среднее значение колебательной скорости

V_k = 4 to • A , получим

Решая систему (7) относительно значения же-~

Q • sin to t         2

сткости, имеем с =--------+ mto , или в пре- x

~ дельном случае при x~A, c = QA

+ m to ² . Тогда

величина нормального напряжения в условиях упругого контакта может быть представлена в форме линейной характеристики

n • A a =

P-C y

to-A +

- P-C

Q = ^—^to-A • Fk

F k

Учитывая то, что возмущающая сила обеспечивается осевыми колебаниями, а возмущающий момент – тангенциальными, а также то, что A τ формируются особой формой УЗ преобразователя, можно установить значение M~

Как видно из выражения (8), уровень мгновенного контактного напряжения пропорционален амплитуде и квадрату частоты. Решаем второе уравнение системы (7) аналогично первому. Для этого перепишем его в следующей форме

~~

M = Q • dA • k • n

/2    '

• •              •

ф + уф = ^ • sin(tot),

где k – коэффициент преобразования, равный примерно тангенсу угла наклона разделяющих пазов волновода; η – КПД преобразования (потери по амплитуде). Приведем систему (5) к следующей форме

где у = у j - приведенный показатель вязкого сопротивления; ^ = MMJ - приведенный возмущающий момент. Таким же образом установим максимум колебательной скорости

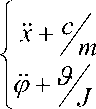
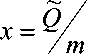
• ^ = M/j

^ф тах

37 to + Y2

M •S

Отсюда получаем выражение момента вязкого сопротивления

е d ^ max

M • < 9² _ M + to² JA_T to J ² + ^² " 2 to²JAj M + 1'

Введя допущение о том, что момент вязкого сопротивления равен моменту, образованному переменным контактным давлением на стороне витка, получим следующее выражение

d ^ax = 7 • Fk • f max          k

2 ,         (10)

~ где f - коэффициент трения в условиях УЗК; 7 - контактное давление, определяемое по формуле (8); d – диаметр витка резьбы. Подставляя в формулу (10) все значения и решая его относительно коэффициента трения, получим окончательно формулу динамического коэффициента трения

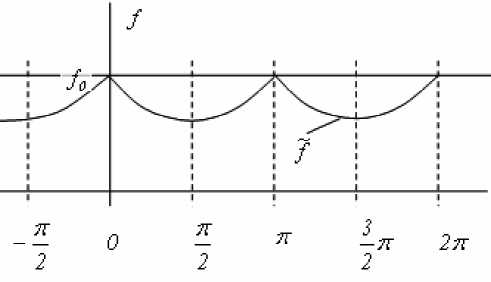
Рис. 3. Характер динамического коэффициента трения

Проинтегрировав функцию f ( t ) , получим

r-W f=

2 M ( M + to² AJ )

to A

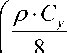
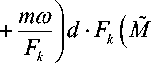
+ 2 to² A _T J )

ПП f = f f (t) dt =f 0 - f to-  - f to3 -

0                        2 0

f

to5

t ⁶

6 • 5!

r* 7

- f to

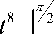
⁸ • ^7!0

Из выражения (11) ясно, что коэффициент трения пропорционален квадрату частоты (числитель) и обратно пропорционален 4-й степени частоты, следовательно, с ростом частоты коэффициент трения снижает свои значения. Однако при одной и той же выходной мощности рост частоты вызывает уменьшение амплитуды колебаний, поэтому монотонной падающей характеристики коэффициента трения от частоты в реальных условиях быть не может, и она имеет более сложный характер. Численные исследования формулы (11) требуют нагрузочных характеристик выходного контура генераторных установок, поэтому для упрощения исследований, можно воспользоваться частной зависимостью коэффициента трения [5], которую можно описать выражением

~ f (t) = fо - f |sin tot|

где f 0 – коэффициент трения покоя; f^* - постоянный коэффициент для определенных условий. Вид зависимости (12) представлен на рис. 3.

Найдя производные высших порядков функции f ( t ) , можно представить ее в виде ряда Маклорена

to5t5            to7t7

—       •--•• • •

5!          7!(13)

или окончательно f (V) = f 0 - f-• П - f-

2 v 2 v

_ 3* _5

П f П f П ---------- 3!2 v 5!2 v 7!

где v – герцовая частота УЗК.

Таким образом, с ростом частоты v степень снижения коэффициента трения уменьшается, т. к. при этом уменьшается и период провалов f * . Представив, что коэффициент f * равен a •v • A , где a - константа, можно переписать выражение (14) в следующую форму

~

^^^^^^^s

Следовательно, рост амплитуды приводит к снижению динамического коэффициента трения.

Выводы: на основании всех полученных результатов можно установить, что в общем виде динамический коэффициент трения уменьшается с ростом колебательной скорости. Однако поскольку изменение частоты УЗК ведет к обратному процессу изменения амплитуды, то зависимость ^{f (}Vk ) имеет неоднозначный характер и может проходить определенный минимум. В любом случае более точные характеристики трения лучше определять экспериментально для подтверждения теоретических выкладок.