Динамический анализ радиоканала случайного доступа системы связи с расширением спектра и ретрансляцией сигналов

Каналы случайного множественного доступа, в которых возможны коллизии, в настоящее время находят широкое применение в системах связи, например, функционирующих в режиме предоставления каналов по требованию [4-5]. В работе рассматривается канал случайного доступа в системе пакетной радиосвязи с ретрансляцией сигналов, временным разделением каналов и шумоподобными сигналами (ШПС), которые формируются на основе «прямой последовательности» (direct sequencing – DS) или «прямого расширения» при помощи псевдослучайных последовательностей (ПСП).

Математическая модель радиоканала случайного множественного доступа

Применение сигналов с расширенной базой в каналах случайного множественного доступа обуславливает наличие явления захвата, которое состоит в согласованной настройке устройства селекции приемника только на один из множества одновременно поступающих на его вход шумоподобных сигналов. Механизм захвата основан на свойстве приемника входить в синхронизм и оставаться в состоянии синхронизации с одним сигналом и подавлять как на- кладывающиеся сигналы, обращаясь с ними как с шумом в случае, если несколько передатчиков одновременно ведут передачу, используя одну и ту же фазу одного и того же шумоподобного сигнала с интервалом задержки больше длительности элементарного символа используемой псевдослучайной последовательности, так и преднамеренные помехи. Наличие явления захвата улучшает показатели качества функционирования радиоканала случайного множественного доступа.

Достигаемая фактическая степень захвата сигналов зависит от конкретных особенностей расширяющей спектр модуляции и обработки в приемнике и точности синхронизации по циклу передачи. Вероятность захвата сигнала в этом случае будет равна

Рз ( k ) = Pt ( k ) P^ ( k ) P ( k ) , (1)

где P _T ( k ) - вероятность разнесения сигналов от k активных передатчиков (абонентов) на величину большую, чем интервал уязвимости; P _hnp ( k ) — вероятность правильного обнаружения синхросигнала одного из k активных передатчиков; Р ^и ( к ) - вероятность правильного приема информационной части при k активных передатчиках.

В силу того, что начало передачи i -го передатчика однозначно определяется величиной ошибки синхронизации по циклу передачи ε_i , то вероятность того, что для каждого из k абонентов величины ошибок синхронизации по циклу передачи оставшихся k – 1 абонентов не попадут в интервалы уязвимости

(^ - T c L<^ i + Т защ )/Т с J + jT ) ± T 0 , j = 0, Z, i = 1, k , гДе ⁸ i G [^{- Т} защ , + ^Т защ ^] ;

z. = ^2T    - ( (£ + + T )- l\ e. + T IT |U /t ;

i           защ        i защ c ⎣ i защ с ⎦ с

T _c – длительность двоичного символа; T_защ – защитный интервал между циклами передачи; τ ₀ – длительность элемента псевдослучайной последовательности; ⎣ ⋅ ⎦ – целая часть, будет равна

PT (k) = Jf(^1 ) Jf(^2 ) - jf(^k Wk d£k-1 ••• dei , (2) D1 D2 Dk где область интегрирования

D = (-T Т )\(-Т  Т ) П i ( ^ защ , защ) x ( защ, защ )

-

∩

ε i ^{+ T} защ

Т с

i -1 z, ∪∪ m = 1 j = 1

ε i - T c

ε + T iзащ

Т с

⎞⎞

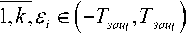
+ jT= - T 0 ,

⎟⎟⎟⎟

+ jTc -τ0  ⎟⎟⎟⎟

⎠⎠

Вероятность правильного обнаружения и приема сигнала определяется видом модуляции, отношением сигнал/шум h ₀ ² на входе приемника и видом помехоустойчивого кодирования [5-7]. При использовании ретранслятора без обработки сигнала выражение для отношения сигнал/шум при k активных передатчиков имеет следующий вид

h02 = B [(v4 + Ycn v3 )(v2 + kKкс + КкЛ ) + v2 +

+Yc (k - 1) + Yсп (КкЛ1 + k (Ккс — 1))] 1

где В - база сигнала; v = ^пб^пс — превышение 1 РсКпп мощности помехи над уровнем сигнала на входе v2 = шб пс – превышение мощ- ности флуктуационногсо шпшума приемника ретран-

Р слятора над уровнем         v = пв – превы-

βРб шение мощности помехи над уровнем сигнала

Р ретранслятора н                    v = ^шв

βР б

–

превышение мощности флуктуационного шума

приемника над уровнем сигнала ретранслятора; β – коэффициент использования мощности пе-Ккс , Ккп – коэ енты комбинационных составляющих сигнала и помехи,                 Кпс ,Кпп ,Кпш – коэф фициенты подавления сигналов, помехи и флуктуационного шума приемной системы, соответственно; Рпв и Ршв - уровни мощности помехи, воздействующей непосредственно на вход приемника и уровень, соответственно; Рс,Рпб,Ршб – мощности сигналов, помехи и шума приемной части ретранслятора на входе последнего, приведенные ко входу приемника.

Таким образом, полученное соотношение (3) связывает отношение сигнал/шум с относительными энергетическими параметрами радиоканала, характеризующими качество приемопередающей аппаратуры: v ₂ ,v ₄ и оценку помеховой обстановки: v , , v ₃ , y _c , Y _cn , К _кс , К кп , а также с числом активных передатчиков k .

Когда воздействие помехи происходит в период захвата преамбулы, то в этомслучае прием осуществляется при неизвестной величине задержки преамбулы, и тогда обнаружение ШПС (обнаружение одного бита преамбулы) на 1-м уровне определяется отношением сигнал/шум уже на выходе коррелятора (согласованного фильтра) q ₀ ² = 2h ₀ ² и числом разрешаемых элементов по задержке. Примем дискретную модель изменения задержки, то есть положим, что задержка сигнала во времени принимает ряд дискретных значений. Число таких значений определяется отношением интервала наблюдения Т н к ширине центрального пика АКФ, равного примерно 1 F , где F — ширина спектра сигнала. Положим, что интервал наблюдения равен длительности сигнала Т с , то есть Т н = Т с . Число разрешаемых элементов по задержке будет равно М _т = Т с /(1 F ) = B п^р , то есть равно базе преамбулы В п .

Если на интервале наблюдения, равном длине одного бита преамбулы, напряжение W на выходе согласованного фильтра (коррелятора) превышает порог W 0 , то принимается решение «сигнал есть», если не превышает – «сигнала нет». Тогда, следуя [1; 6], помехоустойчивость приема бита преамбулы будет определяться вероятностью правильного обнаружения Р Пррав и вероятностью ложной тревоги Р" пт :

пр прав

= 1 "  ( 1 "  Р лт 0 1 — 1 ( 1 "  Рправ 0 ) ,

пр

Р лт = 1 "  ( 1 "  Р лт 0 )    ,             (5)

Р _{прав 0} – вероятность правильного обнаружения сигнала при том дискретном значении Р _лт0 – вероятность ложной тревоги при произвольном дискретном значении задержки, то есть вероятность ложного превышения порога.

Предполагая, что сигнал обладает идеальной АКФ без боковых пиков, имеем [1]

Рправ 0 = J g exP - g + q0 I0 (gqo ) dg , (6) bq0  ⎝⎠ где 10 (x) - модифицированная функция Бесселя b = W0 W – относительный порог. Аналогично

Р- = J g exp (-f k = exp [- b^} (7) bq 0        ⎝²⎠          ⎝²⎠

Таким образом, будем считать, что синхронизация ШПС приемника на любой из k сигналов равновероятна и равна

^T защ

I      If (= > пр ∫ ⎢⎣Тс ⎥⎦ прав                  прав Tзащ

■

Тогда

Р ^ пр ( k ) = 1 "  ( 1 "  Р прав ) k ■           (14)

Возможно организовать прием преамбулы и другим способом, связанным с измерением известной задержки, тогда, следуя [3], прав приема будет следующим: если напряжение на выходе коррелятора на интервале длительности одного бита преамбулы не превышает порога W ₀, то принимается решение «сигнала нет», если же оно максимально при каком-либо дискретн значении задержки и превышает порог, то прин мается решение «сигнал есть» с этим значением задержки. В этом случае P _лт оценивается также, как и (5), а вероятность правильного приема [3]:

∞     _⎛ 22

Р Р» = J g ^exp| — 2^{2 0}

bq ₀         ⎝

_{2 B} пр _{- 1}

I o ( gq o ) j ^{1 -} exp g , I

dg ■(8)

В [3] показано, что при выполнении условия

qo > ^2ln (B^ -1) / b,            (9)

которое на практике выполняется в большинстве случаев, имеет место

₂     B _пр -1

P ^пр прав

Применение при передаче информационной части ШПС с базой В и >  В _пр , а также кодирования сверточным кодом и кодом Рида-Соломона и процедуры перемежения позволяют сделать вывод о том, что при условии обнаружения и синхронизации ШПС вероятность правильного распознания информационной части близка к единице. Тогда P * ( k ) = P пр ( к ) ■

Таким образом, совокупность (2)-(3); (10); (13)-(14) и (1) является математической моделью оценивания вероятности выделения (захвата) шумоподобного сигнала в канале с коллизиями в условиях воздействия помех.

Полученные соотношения позволяют представить процесс функционирования рассматриваемого канала x_t в виде дискретной конечной марковской цепи с N + 1 состоянием.В качестве состояния канала n = {0; 1; 2 … N } принимается число передатчиков, находящихся в режиме повторной передачи.

Матрица вероятностей переходов между состояниями P =|| p_nm ||, где p_nm = P [ x_t = m | x_t-1 = n ], задается выражением:

^P =11 Pnm 11=

0, m <  n - 2

Будем полагать, во-первых, что порог W ₀ выбран таким образом, что вероятность ложной тревоги существенно мала и ее можно не учитывать при нахождении вероятности захвата. Во-вторых, что для правильной синхронизации достаточно принять хотя бы один бит преамбулы, тогда

Р прав ( ^ ) = 1 "  ( 1 " P^ ) l ³ ) , (11)

n

(1 - Po )N ' ” E С P ( 1 - Pr Г Рз ( i ) , m = n - ¹ i =1

C m-n m-n           ^{N -m} ,,

N-n P0   ( 1 - P0 ) ^X

n

XE CnPr (1 - Pr Г‘ (1 - Рз (i + m - n )) + i=0

г m+^-n m +1- n

' N-n p0

N - m -1

(1 - Po )

X

где l3 (^) - количество бит, попадающих в интервал поиска сигнала T = 1„„Т,; L, - число бит в ппрспр синхро-преамбуле.

Количество бит синхро-преамбулы, попадаю-

^X E ^C nPr ( 1 - Pr ) Рз ( ^{i +} m - n ⁺ 1 ) , m ^ n , i =0

где p ₀ – вероятность генерации первичного пакета в начале очередного временного окна; p r - ве-

роятность генерации повторного пакета в начале

щих в интервал поиска сигнала, зависит от величины ошибки синхронизации по циклу передачи следующим образом:

очередного временного окна;

i

l3 (^) =

Tп-ε

Т с

Ci =jj!(i - j )!

для j ≤ i

0          для j >  i

iи j - положительные числа.

В силу эргодичности и регулярности рассматриваемой цепи Маркова существует стационарный вектор вероятностей состояний канала П = ( п о ; n i ^ n N ), удовлетворяющий следующим уравнениям:

⎧ ^N

^П m = У ^П n P nm ’    m = ⁰ , ^N

⎪            n =0

N

У П n = 1.

⎩ n=0

Найдем ожидаемый стохастический дрейф в условиях захвата сигнала

N dr(n) = У ( m - n )p„m = m=0

N-n

= ( N - n ) p o - У C NN_n p ^kk ( 1 - p o ) N-n-k (19) k = 0

n хУ СПPr (1 - Pr ) Рз (i + k).

i = o

Показателями качества радиоканала выступают пропускная способность канала (в пакетах на сегмент) и среднее время задержки пакета (в сегментах), определяемые следующими выражениями:

Nn С=∑πnan,T=, n=0            С

• c ( n )⁽³⁾

G ₀ ,c,dr,π

c ( n )⁽²⁾

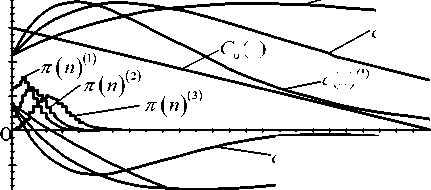
G o (n)

c ( n ) ⁽)

N dr (п)т dr (n)3-1

где

dr ( n )^{l -2)}

Рис. 1. Динамический анализ радиоканала ( p^¹ >  РР >  P?' )

N-n

N—n— 1 n

aⁿ ) = E C -n p 0 ( 1^- P o )    E Cp r ( 1^- P r )

i = 0

I ' p (i+j)+

N-n

+(1-Pr )n ECn—nP (1-Po )    P (i) — i=1

– пропускная способность радиоканала в n-ом N состоянии; n = ∑nπn – среднее число передат- n=1

чиков, находящихся в режиме повторной переда чи пакета.

Динамический анализ поведения радиоканала в условиях изменения трафика и воздействия помех

Динамический анализ поведения радиоканала случайного множественного доступа в различных условиях первичной нагрузки p o , параметра протокола pr и вероятности захвата Рз ( к ) , как характеристики помехоустойчивости целесообразно проводить на основе анализа динамики условных средних изменений состояний радио-каналаканала. Для этого воспользуемся понятием ожидаемого стохастического дрейфа.

Под ожидаемым стохастическим дрейфом будем понимать условное математическое ожидание изменения состояния канала в очередном временном сегменте при условии, что перед этим канал находился в состоянии n dr ( n ) = M [m — n| n ] = У ( m - n ^Pmn . (18)

m ∈ S

Анализ (19) показывает, что ожидаемый стохастический дрейф канала в условиях захвата пакета равен разности между первичным трафиком и относительной пропускной способностью канала по запросным пакетам с(п) в состоянии n , то есть dr (n) = G0 (n) - c(n).           (20)

На рис. 1-3 приведены графики зависимостей с и и = 1, N

и

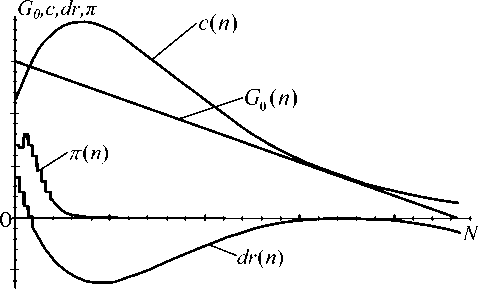
Рис. 2. Поведение радиоканала в оптимальном режиме ( p_r^опт )

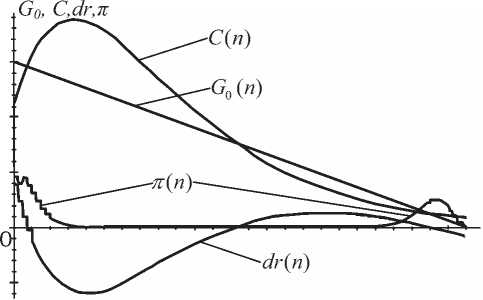
Рис. 3. Поведение радиоканала в бистабильном е-жиме ( p_r> p_r^опт )

Динамический анализ графических зависимостей показывает, что:

- при относительно небольших значени- p _r в канале имеет место только одна точка стохастического равновесия, при этом распределен ие вероятностей состояний канала п (n | n = 1, N ) является унимодальной последовательностью с математическим ожиданием п, почти (с ± А <  1 ) совпадающим с точкой стохастического равновесия (см. рис.

p _r точка стохастического равновесия (dr(n) = 0) смещается влево и, следовательно, уменьшается математическое ожидание числа передатчиков, находящихся в режиме повторов пакетов n . Отсюда, согласно (17), повышается качество канала;

p_r появляется вторая, а затем и третья точки стохастического равновесия (см. рис. 2-3). При этом распределение в ероятностей состояний кан ала п ( n | n = 1, N ) модифицируется из унимодальной последовательности в бимодальную. Появление второй моды в состоя- N , связано с появлением второй устойчивой точки стохастического равновесия и приводит к резкому смещению n вправо (то есть математическое ожидание числа абонентов,находящихся в режиме повторов запросных пакетов, резко возрастает). Следовательно, происходит значительное ухудшение качества канала.

Сделанные выводы не противоречат, а в основном, совпадают с результатами бимодальности состояний процедур типа ALOHA, полученными в [8-9] для асимптотических моделей однородных абонентов.

Оптимизация характеристик канала

Таким образом, при управлении протоколом, качественной границей оптимизации парамет- p _r можно считать максимально возможные значения, сохраняющие унимодальность распределен ия вероятностей состояний канала п ( n | n = 1, N ) . Тогда условие оптимальности канала имеет вид

p* = arg[{dr(n | n = [0, N ]) = 0 ^ double}]. (21) { P r ^}

Следует заметить, что в силу трансцендентности уравнения в фигурных скобках и целочис- n в (19), его решение возможно только путем последовательного анализа знака dr ^{( n )} , нахождения пар таких и и n + 1, при которых dr(n) меняет знак на противоположный. Тогда за решение этого уравнения можно принять решение уравнения вида

dr (n‘r) + (dr(nfs) - dr (ntr))(nx - ntr) = 0, (22)

где их - непрерывное значение n; nr,nfs -последовательньie значения n (nfs -n*' = 1), при которых соответствующие значения дрейфа dr (nlr) и dr (nfs) меняют знак на противоположный. Отсюда следует, что dr (ntr)

nx = n tr------- -.—г .

dr (n fs) - dr (ntr)

Однако, анализ вида показателя средней задержки пакетов показывает, что его минимум достигается при максимуме его пропускной способности. Таким образом, в основу оптимизации параметра канала может быть положена максимизация его пропускной способности. Поэтому найдем условие максимума пропускной способности в n -ом состоянии канала.

Допустим, что p0 = pr = p ^ 0; N ^ »; G = G0 + Gr = pN = const, тогда пропускная способность в условиях захвата пакета будет равна f P3 ( k ) G k C t1

Возь

dC

dG =

∞

=∑ k=1

P ₃ ( k ) G ^k ' e" G k!

( k - G ) .

Тогда нагрузка, при которой будет максимум пропускной способности, определяется из уравнения

s P G     (k - G)=0.      (26)

k = 1            ^k'

Так как при достаточно большом числе активных абонентов к (на практике k >  40) и любых внешних воздействиях вероятность захвата равна нулю, то можно ограничится 40 членами суммы (25).

Анализ уравнения (26) с учетом того, что левую часть можно заменить конечной суммой с с Y = 40 членами показывает:

• -    каждый член суммы может равняться нулю только при G = k ,( G >  0);

• -    G ≤ 1 все члены суммы положительны, а, следовательно, и сумма положительна;

G= Y все члены суммы отрицательны, кроме последнего, который равен нулю, следовательно, и сумма отрицательна.

Уравнение (26) имеет решение 1 <  G sup <  Y, притом единственное. А так как знак производной (25) меняется с положительного на отрицательный, то, в силу достаточного условия макси- G ^sup имеет максимум. Следует отметить, что в силу трансцендентности уравнения (26), его решение возможно только известными численными методами.

В случае конечного числа абонентов нагрузка на сеть в n -ом состоянии канала будет определятся выражением

G ( n ) = ( N - n ) p ₀ + np_r .         (27)

Тогда условием максимума пропускной способности в n -ом состоянии канала будет условие

• (    N - n ) p ₀ + np _r = G sup .        (28)

Особый интерес вызывает поведение радиоканала при увеличении трафика и уровня помех (уменьшении вероятности захвата Р з ( k| k = 1 ) ) при поддержании оптимального режима, выбором соответствующего параметра p _r . Если возмущение первичного трафика в прогнозируемых пределах практически не влияет на положение первой точки устойчивого равновесия (см. рис. 4), то увеличение уровня помехи сдвигает первую точку устойчивого равновесия вправо (см. рис. 5). Такое смещение первой точки устойчивого равновесия,может выводить среднее время задержки за пределы допустимого значения при стохастическом колебании в области данной точки.

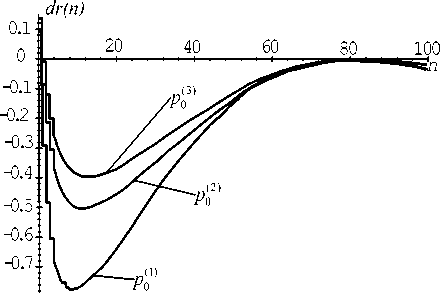
Рис. 4. Поведение радиоканала в оптимальном режиме при увеличении трафика ( Pq¹ <  р ^ ² <  р^ )

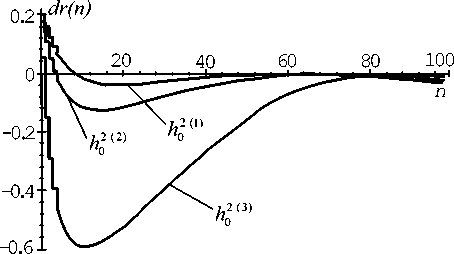
Рис. 5. Поведение радиоканала в оптимальном режиме при увеличении уровня помех (h ₀ ^{2 (1)} <  h ₀ ^{2 (2)} <  h ₀ ^{2 (3)} )

Заключение

Проведенный динамический анализ поведения радиоканала множественного доступа в условиях возмущения трафика и воздействия помех показал, что оптимальный режим его функционирования лежит на границе бистабильного режима.

Таким образом, актуальным становится вопрос о сохранении рассматриваемым радиоканалом свойства робастности (успешности функционирования) в условиях увеличения первичного трафика, воздействия помех и, как следствие, попадание в бистабильный режим.