Динамический анализ трехмассовой системы с учетом технологического сопротивления
Автор: Юнусов С.З., Гапиров А.Д., Кенжаев С.Н., Туракулов М.Р., Халмурзаев Б.Х.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 5 (95), 2023 года.
Бесплатный доступ
В статье рассматривается динамический анализ трехмассовой системы с учетом технологического сопротивления, на основе решения которого, приведены полученные графические зависимости размаха колебаний угловой скорости рабочего вала, неравномерности вращения валов привода, крутящего момента на валу электродвигателя.
Динамика, колебание, угловая скорость, неравномерность вращения, крутящий момент, движущий момент, рабочий вал
Короткий адрес: https://sciup.org/140299527
IDR: 140299527
Текст научной статьи Динамический анализ трехмассовой системы с учетом технологического сопротивления
Определение влияния основных параметров трехмассовой колебательной системы на ее динамические характеристики позволит расширить резонансную зону, которая влияет снижению нестабильности рабочего режима при изменении технологического сопротивления системы является актуальной. Известно, что производительность технологических машин и качество получаемый продукции зависит от технических параметров. Нами ведутся работы по разработке новой конструкции составной ременной передачи, для обоснования параметров изучили динамику движения системы с ременной передачей.
В рассматриваемой трехмассовой системе требуется обеспечение крутильных колебаний третьей массы с необходимой амплитудой и частотой при воздействии внешнего момента, то есть технологического сопротивления.
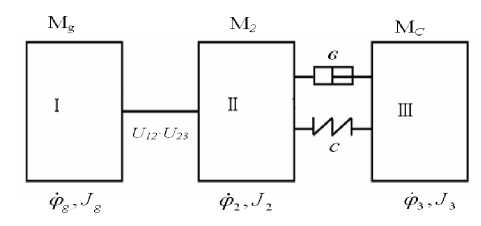
Рис.1. Расчетная схема трехмассовой системы с ременной передачей
Для обеспечения вышеуказанных режимов работы системы решена задача динамики в виде машинного агрегата. При этом следует обосновать и рекомендовать инерционные, а также упруго-диссипативные параметры системы. Система дифференциальных уравнений, описывающие движение трехмассовой системы ускорителя сырцового валика пильного джина имеет вид:
Mg
=
2
ML»-
-
2
Mk
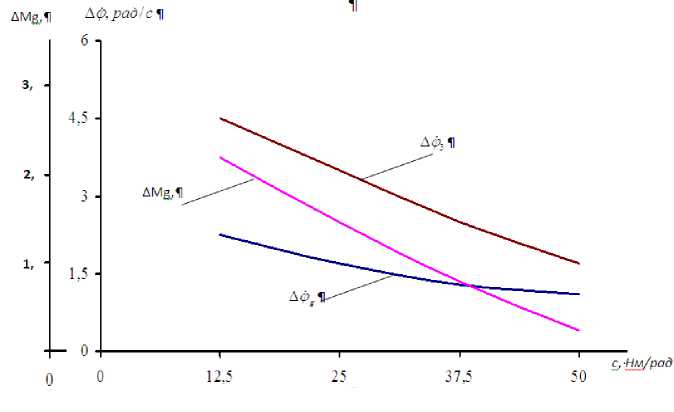
P д- ®cSkMg; JSVg = Mg — U-1M12 J2Ф2 — M12 c(^2 U23Ф3 ) в-(ф2 U23Ф3 ) J3Ф3 — U23cФ2 - U23Ф3)+ Щ3Ь(Ф2 - U23Ф3 )—Me Mc — Mx — Mo sin rot где, Mg, Mk-движущий и критический моменты двигателя; ωс-угловая частота сети; ф, фг, фъ -угловые скорости ротора двигателя, промежуточного и вала ускорителя, с-1; U12, U23- передаточные отношения редуктора и упругой передачи; Sk-критическое скольжение двигателя; Мс - момент сопротивления от технологической нагрузки, Н·м; ω-частота изменения сопротивления; М1, М0-постоянное и амплитудное составляющие момента технологического сопротивления; М12 –взаимодействующий момент между первой и второй массой. Решение задачи осуществляли при следующих исходных значениях параметров: электродвигатель с короткозамкнутым ротором марки 4А90L4У3 [1] со следующими параметрами: N=2,2 кВт; n=1423мин-1; Мк=Мн·2=29,52 Н·м; Мн=9550·(N/n)=9550·(2,2/1423)=14,76 Н·м; fс=50 Гц; Р=2; ωс=2πfс=314 рад/с; ωн=πn/30=3,14·1423/30=148,9 рад/с; ωо=2πfс/Р=2·3,14·50/2 =157 рад/с; Jд=GD2/4g=0,24/4·9,81=0,061 Н·мс2; Sн= (ωо- ωн)/ ωо=(157-148,9)/157=0,051; Sk — х- SH (1 + V1 — 1/Я2)— 2 ■ 0,061(1 + V1 —1/22)— 0,2269; Коэффициент жесткости упругой передачи:с=18÷54 Нм/рад; Коэффициент диссипации упругой передачи: b=2÷4,6 Н·м·с/рад. На основе полученных решений построены графики, характеризующие движение машинного агрегата, определен максимальный размах колебаний угловой скорости рабочего вала, неравномерность вращения валов привода ф>g, фЬ2, ф3 и крутящий момент на валу электродвигателя Mg. Известно, что математическая модель машинного агрегата позволяет изучение переходного процесса пуска системы. Из полученного решения задачи видно, что при расчетных значениях параметров системы в основном выходит на установившийся режим за 0,1÷0,15 с., а с учетом дополнительных угловых колебаний вращающихся масс за счет упруго – диссипативных свойств в системе переходной процессе пуска затягивается до 2,2÷2,6 с. Следует отметить, что для уменьшения времени переходного пуска машинного агрегата целесообразным считается уменьшение суммарного момента инерции вращающихся масс, увеличение коэффициента диссипации упругого элемента (резины). При этом для увеличения неравномерности δg, δ2, δ3 эффективным является уменьшение момента инерции рабочего вала. Это объясняется тем, что возмущение приводящий к неравномерности угловых скоростей системы приложено к третьей массе [2]. На рис. 2. представлены графические зависимости изменения движущего момента двигателя и размаха угловых скоростей. Анализ зависимостей показывают, что увеличение нагрузки Мс приводит к возрастанию не только нагрузки на электродвигатель, но и увеличению размаха колебаний угловых скоростей вращающихся масс системы. Так, при увеличении Мс от 30 Нм до 95 Нм, нагрузка на двигатель возрастает до 20÷21 Нм, размах угловой скорости выходного вала повышается до 4,6 рад/с. Кроме того при возрастании Мс до 95 Нм, средние значения угловых скоростей уменьшаются по нелинейной закономерности, так ф уменьшается от 151,7 рад/с до 144,9 рад/с, а ф3 от 29,8 рад/с до 25,7 рад/с. Рис.2. Зависимости изменения движущего момента двигателя, размаха угловых скоростей масс машинного агрегата от изменения технологического сопротивления где, 1- Mg=f(Mc); 2 - Ар^=f(Mc);3- Ар2= f(M);4- Ар i=f(Mc) На рис. 3. представлены полученные графические зависимости изменения размаха колебаний нагрузки на привод ЛМ§ и угловых скоростей Аф§, Ар2, Ар3 от изменения круговой жесткости упругой втулки. Так увеличение жесткости от 13,5 Нм/рад до 54 Нм/рад размах угловой скорости ускорителя сырцового валика уменьшается от 4,6рад/с до 1,4 рад/с, а Ар)g от 3,1 рад/с до 1,2 рад/с. При этом размах ^Mg уменьшается от 2,85 Нм до 0,35 Нм. Это объясняется тем, что с увеличением круговой жесткости упругой втулки системы как бы становится единым (ближе к одномассовой) или передаточные отношение между массами приближаются к постоянному значению. Учитывая, что для обеспечения необходимых (из условий технологического процесса) значений неравномерности δ3=0,11÷0,15 наиболее рациональнымыми значениями коэффициента круговой жесткости упругой передачи является (36÷54) Нм/рад. Для уменьшения времени переходных процессов в машинном агрегате целесообразным считается увеличение коэффициента диссипации упругой элемента. Для обеспечения времени пуска системы до (0,8÷1,5) сек. и значительного снижения переходных процессов в установившемся режимах движения машинного агрегата рекомендуемыми значениями коэффициента диссипации являются b=(3,5^4,0) Нмс/рад. Рис. 3. Зависимости изменения размаха колебаний нагрузки на двигатель и угловых скоростей масс системы в функции коэффициента круговой жесткости упругого элемента где, 1-k Кроме этого, представлены графические зависимости изменения движущего момента двигателя и размаха угловых скоростей. Анализ зависимостей показывают, что увеличение нагрузки Мс приводит к возрастанию не только нагрузки на электродвигатель, но и увеличение размаха колебаний угловых скоростей вращающихся масс системы. На основе динамического анализа трехмассовой системы пильного джина с учетом технологического сопротивления построены графики, характеризующие движение машинного агрегата, определен максимальный размах колебаний угловой скорости рабочего вала, неравномерность вращения валов привода ф, фг, ф3 и крутящий момент на валу электродвигателя Mg.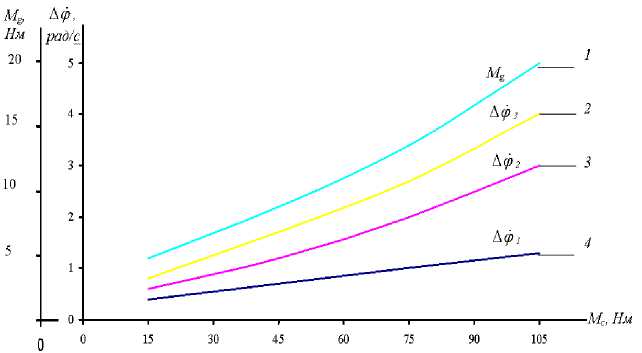
Список литературы Динамический анализ трехмассовой системы с учетом технологического сопротивления
- Кравчик А.Э, и др. "Асинхронные двигатели серии 4АМ". Энергоиздат, 1982 г, 504 с.
- Зедгенизов В.Г, Файзов С.Х. "Исследование влияния основных параметров двухмассовой колебательной системы на ее динамические характеристики".


