Динамический расчет композитных стержневых систем при кинематических воздействиях

Композитные стержневые системы относятся к разряду новых конструктивных систем, позволяющих при условии рационального проектирования создавать эффективные инженерные решения несущих конструкций, адаптированных к напряженно-деформированному состоянию, обладающими повышенной несущей способностью, жесткостью, трещиностойкостью при одновременном снижении расхода материалов. Однако в настоящее время в силу недостаточной изученности они пока не нашли широкого практического распространения.

В статье рассматриваются задачи динамического расчета произвольных плоских стержневых систем, образованных из неоднородных (композитных) профилированных стержней при комплексном воздействии, в котором наряду с наличием нагрузок и температурного поля, учитываются и кинематические факторы – заданные смещения некоторых узлов и (или) заданные обобщенные деформации некоторых стержней системы. Первое возникает в условиях «жесткого» нагружения, что наблюдается в случае значительного различия жесткостных характеристиках конструкции и взаимодействующих с ней объектов нагружения, при воздействии сейсмических сил, сил морозного пучения и т. п. Второе – при учете влияния внутренних кинематических факторов – случайных и детерминированных несовершенств, а также специально вводимых «регуляторов» состояния системы, применяемых в задачах регулирования и расчета управляемых конструкций [1].

1. Основные соотношения. Плоская стержневая система образована из прямолинейных ком- позитных стержней, имеющих неоднородную структуру [2] и формы поперечных сечений, показанные на рисунке. В системе координат xyz стержень обладает свойствами симметрии относительно плоскости xy – силовой плоскости, продольная ось совмещена с осью x . Материал каждой фазы представляет собой сплошную, однородную линейно вязкоупругую среду. Длина и характерный поперечный размер стержня удовлетворяют условию l > (5 + 6) h. Используется сдвиговая модель стержня Тимошенко.

Для стержневой системы, имеющей n_s стержней и m_u узлов, сформируем векторы: обобщенных концевых усилий S ( t ) и деформаций L ( t ) стержней (индексы: b – begin , e – end ), узловых динамических нагрузок F ( t ) и перемещений W ( t ) :

S ( t ) = [ S 1 . S _y . S n s ] ^T,

S/ t ) = [ N M b M e ] T ,

L ( t ) = [ L . L _y . L n s ] T ,

L/ t ) = [ A l 0 b 0 e ] T ,                         (1)

F ( t ) = [ F 1 ™ F , ™ F „_m ] T ,

F _; ( t ) = [ F x F y m ] T ,

W(t) = [w1 .„wi wmu ]T, w i (t) = [ wX wY Wp] T .

а)

б)                   в)

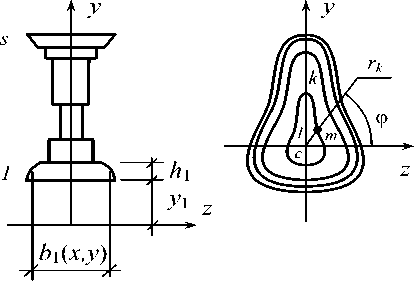
Поперечные сечения композитных стержней: общего вида (а), поперечно-слоистое (б), полярно-слоистое (в)

Для j -го стержня вектор S _j содержит независимые компоненты концевых усилий, а вектор L _j – полные (термосиловые) обобщенные деформации: удлинение A l и повороты 9 _ь , 9 e концевых сечений.

Систему основных уравнений, состоящую из уравнений движения, геометрических и физических равенств, представим в виде [3]

AS ( t ) + F ( t ) = M w W ( t ),

< AтW(t) + L(t) + L + AL(t) = 0, (2) B-1 [L(t) - Lt ] + B. L(t) = S(t), где A – матрица преобразования силовых базисов концевых усилий в стержнях к глобальным осям, B = diag[B1...B n ] – матрица податливости по направлению обобщенных деформаций L , B V = diag[B V 1...BVn ] - матрица вязкой текучести по направлению скоростей L , MW – инерционная матрица системы; L , LT – векторы обобщенных геометрических несовершенств и свободных температурных деформаций со структурой, аналогичной вектору L, AL(t) - вектор регуляторов обобщенных деформаций, W – вектор узловых ускорений.

Система уравнений (2) может быть сведена к разрешающему дифференциальному уравнению в перемещениях

I R ' = R F (t) + R T + R 5 + R C (t) (3) r=0 dt с начальными условиями W(0) = W0 , W(0) = W0 . Здесь R0 = AB-1AT – матрица жесткости, R1 = ABV1AT - вязкого сопротивления, R2 - инерции; сумма векторов в правой части отражает воздействие внешних факторов: RF (t) = F(t) - динамических нагрузок, RC (t) = -A(B-1AL + B-1AL) -регуляторов обобщенных деформаций,

R _T = - AB 1 L _T - температуры, R ₅ = - AB *L -геометрических несовершенств стержней системы.

2. Кинематическое воздействие в форме заданных динамических смещений узлов . Пусть среди m = m ₀ + m 1 компонент вектора W ( t ) имеются m ₀ компонент, изменяющихся по заданным законам и m ₁ – искомых компонент свободных перемещений. Набор m ₀ перемещений, с учетом структуры составляющих векторов w _i ( t ) , может быть произвольным и иметь смысл поступательных перемещений узлов w_X , w_r и поворотов w _ф . Перегруппируем элементы исходного вектора перемещений, объединив в блок W ₀ заданные величины, а искомые - в блок W 1 : W ^ [ W ₀ W 1 ] ^т. Обратный переход к исходным перемещениям может быть выполнен на основе преобразования

W = H w [ W 0 W ] т (4) при помощи адресной матрицы H _W = { h j }, элементы h ij = {0; 1} которой отражают принадлежность (в случае h ij = 1) j -го элемента вектора

[ W 0 W 1 ] т i -му элементу вектора W . Перегруппи-

ровка перемещений приводит к разделению матричных коэффициентов и векторов воздействий в

(3) на блоки

R r ^

R r ,00 R r ,01

R r ,10 R r ,11

R ^

R 0

R 1

и записи системы уравнений (3) в виде

I R r,00

r = 0

^

I R r ,10

. r = 0

d^r W 0 ( t ) dt^r

+ I R r ,01

r = 0

( r = 0,1,2)

d^r W ₁( t ) dt^r

= R q ( t ),

d^r W q ( t ) _{+    R}    d^r W 1 ( t )

dt    r ¹ r ¹   dt

= R 1 ( t ),

R i ( t ) = R _fi ( t ) + R T + R_&. + R _a ( t ), ( i = 0,1).

Отсюда с использованием второго уравнения для функций свободных перемещений имеем дифференциальное уравнение t R,,, d^H = R,(t)(5)

r=0

R,(t) = R F,(t) + R T, + r51 + R C,(t) -tR r ,10 —77^ r=0

с заданными начальными условиями для W ₁(0) , W 1 (0).

Решение однородной задачи, соответствующей (5), представленное в виде W , ( t ) = W e ^X t , W = [ £ , ... ^ l ]^T , может быть построено известными способами на основе уравнения ( X ² R ₂₁₁ + X R ,,, + R _o11) W = 0 с характеристическим равенством степени 2 m ₁ относительно частотного параметра X

|^X2 ^R 2,11 ^{+ X R} 1,11 ^{+ R} 0,111 = ⁰ .

Рассмотрим получение частного решения уравнения (5) при кинематическом воздействии в форме заданных смещений W0 и отсутствии дей- ствия регуляторов (AL(t) = 0). Правая часть при- нимает вид R,(t) = —tRr,10drW0(t)/dtr . Реше-r=0

ние будем искать в тригонометрической форме, представив векторы заданных и свободных перемещений в виде частичных сумм рядов Фурье с удержанием одинакового числа членов j 0

^W 0⁽ t ) = E ( C 0 7 ^c os j ® f t ⁺ S O j sin j ® ft ) ,    ⁽⁶⁾

j = 0 j 0

W , ( t ) = t ( C , j cos j ® f t + S , j sin j Ю f t ) ,    (7)

j = 0

где          to f = 2 л / T ;          C Oj = ^[ c l j c 2 j ... c m , j ^{] T} ,

Подстановка (6), (7) в (5) в рассматриваемом случае воздействия дает систему уравнений для векторов C , j , S , j в j -й гармонике ( j = 0,..., j ₀)

^{( R} 0,11   j 27 ^R 2,11^{) C} 1 j ⁺ j ^to f ^R 1,11 ^S 1 j =

= ^{- ( R} 0,10 ^— j 2 ®/ ^R 2,10^{) C} 0 j - j ^to f ^R 1,10 ^S 0 j , ^— j ^to f ^R 1,11 C 1 j ^{+ ( R} 0,11 ^- j ^to f ^R 2,11^{) S} 1 j = _= - ( R o,io - j² to f R 2,1o ) S o j + j to f R 1,10 C 0 j

После нахождения перемещений W ₁ ( t ) переход к исходной структуре вектора перемещений W ( t ) выполняется с помощью преобразования (4).

• 3.    Воздействие регуляторов обобщенных деформаций A L ( t ). Данный вид воздействия отражает стационарное или динамическое изменение компонент вектора A L j ( t ) - удлинения A l ( t ) и (или) поворотов 9 b ( t ), 9 e ( t ) концевых сечений, что может быть реализовано в решениях прямых задач и задач регулирования НДС системы, когда посредством применения специальных жестких вставок в композитные стержни указанные деформации изменяются по заданной программе в управляющем блоке. Технически это может быть реализовано поворотными или поступательными устройствами на механической, гидравлической, электромагнитной и иных основах.

• 3.1.    Случай упругоподатливых элементов, содержащих регуляторы, может быть исследован на основе дифференциального уравнения (5) с удержанием в правой части слагаемого R C ( t ) = — A ( B ^{— 1} A L + B p -^L ). Формально с точностью до обозначений и размерностей векторов и матриц этот случай эквивалентен вышерассмотренному в п. 2 кинематическому воздействию. Применяя для A L аппроксимацию (6), а для W -(7), приходим к системе уравнений типа (8) относительно искомых числовых векторов, используемых в перемещениях узлов системы W .

• 3.2 .    Построение решения на основе уравнения (5) при наличии жестких регуляторов, в силу вырождения для них матриц жесткости, требует применения специального алгоритма матричных блочных исключений.

При этом возможны два случая. В первом из них жесткие вставки занимают относительно небольшой объем в деформируемом элементе, что приводит к суммированию деформаций L + A L в геометрическом уравнении (2). Во втором – весь стержневой элемент является жестким регулятором с нулевой податливостью и деформацией L — L т = 0.

Пусть среди n = n h + n e компонент обобщенных деформаций системы n_h компонент изменяются по установленным законам, представленными n h компонентами вектора A L ( t ). Число заданных таким образом компонент не должно превышать суммарного числа степеней свободы узлов системы ( n h <  m ). В соответствии со структурой вектора L _j (1) могут быть реализованы три типа стержней: нерастяжимые ( A l = 0 , 9 b * 0, 9 _e * 0), неизгибаемые ( A l * 0 , 9 b = 0, 9 _e = 0 ) и абсолютно жесткие ( A l = 0 , 9 b = 0 , 9 _e = 0 ).

Перегруппируем компоненты в векторах обобщенных деформаций, переставив в начало блоки, соответствующие заданным деформациям. Также преобразуем и вектор усилий:

A L ^		rA L h 1 La l e J		, L ( t )	~^	[ L h 1 L L e J
	"L,."			S ( t ) ^	F s	1
L ^		h *	,				.
	L L e J				L S	e J

, ^L T ^

L

L

Th

’

¹ Te _

Аналогично преобразуем матрицу A ( m x n ) условий равновесия, B ( n x n ) - податливости и B V ( n x n ) - вязкой текучести системы (2)

A ^ [ A h A e ^] , B ^

■ B h 0 1 . 0 B e J

,

B v ^

^B Vh   ⁰

0 B Ve

.

В последующем будем учитывать, что L h — L Th = 0, A L e = 0, B h = 0, B vh = 0.

Для обеспечения возможности последующих блочных исключений выделим из матрицы коэффициентов [ A h A e ] уравнений движения квадратный невырожденный блок A _hh , применив процедуру Гаусса с n_h шагами и перестановкой строк. В результате получим следующие перегруппировки векторов и матриц

A ^ W ^ Ahh Akh [ Wh 1 L Wk J A he " A ke _ , F , M ^ ГМ LM ^ "Fh" _Fk _ nk = m - nh det(A hh) * 0. hh kh

M

M

hk

’

- kk J

Здесь первый индекс обозначает число строк, а второй – число столбцов с использованием соответствия h о nh, e о ne, k о nk . В результате преобразований (9)–(10) три уравнения (2) приобретают структуру

••

••

A hh S h + A he S e + F = M hh Wh + M hk Wk ,

••

••

I A kh ^S h + A ke ^S e + F k = ^M kh Wh + ^M kk Wk , A hh ^W h + A kh W k + L h + L Th + ^{A L} h = 0, A he W h + A ke W k + L e + L e = 0,

B — ‘ ( L e — L Te ) + B — 11L e = S e .

системы

Исключив из (11) S _h и выразив из (12) W _h , а из (13) – S _e , получим

M kkWk + M kh W h + ( A ke

—

A kh A hh A he ^{) S} e ^{+ R} kF = 0,

. W h =— ( A hh ^( A k ,W k + L h + L Th +A L h ), S e =— B e ^{— 1}( A T e W h + A L W k + L e + L Te ) — _     - B v 1 ( A т e W h + A ke W k ).

Наличие nh жестких элементов уменьшает на nh число степеней свободы системы, вследствие чего вектор перемещений W будет содержать подвектор Wh зависимых компонент. Выполнив ис- ключение векторов Wh и Se из системы (14), окончательно получим дифференциальное уравнение второго порядка в перемещениях, аналогичное (5):

f R.d^ = R. (t),(15)

r ,kk r r=0

~        . .          ____ . .         ____ ____  . .

Rk (t) = RkF (t) + RkT + Rk5+ RkCL (t)

с матрицами жесткости R _{0, kk} , вязкого сопротивления R _{1, kk} и инерции R _{2, kk} по направлению независимых компонент вектора W _k и его производных: _—

^R 0, kk = ^M kk ^{— M} kh ⁽ A hh ) A kh ,

^R 1, kk = V kk ^— V kh ⁽ A hh ) A kh , 6     5 l А ^т k^—1 А^т

R2,kk = Rkk Rkh (Ahh ) Akh с компонентами вектора свободных членов (16), отражающими силовое, температурное воздействия, наличие начальных несовершенств и жестких регуляторов обобщенных деформаций

R kF ( t ) = — F k ( t ) + A kh A hh F h ( t ),

R kT = ( A ke — A kh A hh A he ) B — 1 L Te — R kh A hh L h ,

R k 5 = ( A ke — A kh A hh A he ) B — 1 L e — R kh Ahh L h ,

R kCL ( t ) = — M kh ( A T h ) ^{— 1} A L h —

- V kh ( A T h ) ^{— 1} A L h — R kh ( A T h ) ^{— 1} A L h .

В уравнении (15) использованы редуцированные инерционные матрицы M по направлению ускорений W _k , W _h , редуцированные матрицы вязкого сопротивления V по направлению скоростей W _k , W _h , редуцированные матрицы жесткости R по направлению перемещений W _k , W _h : _—

^M kk = ^M kk ^— A kh A hh ^M hk , -„                    _—

M kh = M kh ^— A kh A hh ^M hh ,

V kk = ( A ke — A kh A hh A he ) B V1A^Tke ,

V kh = ( A ke — A kh A hh A he ) B V\ A h_e , R kk = ( A ke — A kh A hh A he ) B — ‘A ke , R kh = ( A ke — A kh A hh A he ) B e ^— ‘ A hee .

Решение уравнения (15) при кинематическом воздействии R _kCL ( t ) может быть выполнено по схеме, рассмотренной в п. 2. Для этого, записав аппроксимацию (6) для вектора A L _h , а (7) - для W _k , приходим к системе уравнений типа (8) для искомых числовых векторов в (7).

Если nh < m, то, как следует из рассмотренных выкладок, в композитной системе могут быть заданы произвольные обобщенные деформации ALh. В случае если число жестких элементов nh > m получаем переопределенную систему, для которой условия совместности в (2) не могут быть выполнены при произвольных компонентах ALh . При nh = m блочные исключения не требуются, а искомые перемещения могут быть найдены сразу из кинематических соотношений (2) при L( t) - LT = 0

W ( t ) = - ( A ^t) ^{- 1}[ L + L _T + A L ( t )].

• 4.    При использовании упругоподатливых регуляторов A L может быть поставлена задача ограничения общей жесткости системы

I W ( t )| = | f w [ A L ( t )]| <  W adm , (17) где W _adm – вектор нормируемых величин узловых перемещений. Условие (17) в пространстве компонент вектора A L задает области допустимых состояний системы.

Рассмотрим постановку динамической задачи проектирования композитной системы с заданными стационарными узловыми перемещениями , что соответствует выполнению условия (17) в форме строгого равенства. Примем число упругоподатливых регуляторов в дифференциальном уравнении типа (5) равным n h = m <  n . Считая фазу переходных процессов с наличием собственных колебаний завершенной, обратимся к частному решению системы уравнений. При реализации стационарных перемещений W ( t ) = W _adm уравнение (5) принимает вид

R o W adm = F ( t ) - AB ^{- 1} L T - AB - 1 L -

• - A [ B ^{- 1} A L ( t ) + B ^ -1 A L ( t )].

Отсюда получаем систему дифференциальных уравнений первого порядка нормального вида относительно искомых компонент вектора регуляторов обобщенных деформаций A L ( t )

— A L ( t ) = G A L ( t ) + G_o ( t ), (18) dt ⁰

G = -Bv B-1, с вектором внешних воздействий Go (t) = BV A-1 [F(t) - RoWadm ] - BVB-1 (IL - Lt ).

Методы решения таких систем известны. В частном случае, полагая в (18) W _adm = 0, имеем задачу регулирования деформируемой композитной системы с неподвижными узлами .

Выводы. Изложенные способы матричных расчетов композитных стержневых систем при термо-силовом и кинематическом воздействиях могут быть применены для широкого круга практических приложений, в постановках прямых и оптимизационных задач композитных стержневых систем, в частности:

• а)    при горизонтальных сейсмических воздействиях, возникающих в результате распространения в грунтовой среде продольных волн растяжения–сжатия. Для этого в векторе W ( t ) учитываются компоненты w_X ( t ) перемещений опорных узлов. Аппроксимация (6) позволяет каждую из них задать различными функциями времени, что дает возможность описать прохождение сейсмической волны по протяженному сооружению;

• б)    при вертикальных сейсмических воздействиях, возникающих в результате распространения поперечных волн, сопровождающихся деформациями сдвига грунтовой среды и искривлением земной поверхности. В этом случае в опорных узлах учитываются компоненты w_Y ( t ) , а при необходимости и повороты н ;_р ( t );

• в)    в задачах статического и динамического регулирования напряженно-деформированного состояния системы. В этом случае с использованием ограничений, формируемых для свободных перемещений W ₁ , обобщенных деформаций L , усилий S (а также – для соответствующих величин в промежуточных сечениях композитных стержней, определяемых через компоненты указанных векторов) устанавливаются условия регулирования для варьируемых перемещений W ₀( t ) , обобщенных деформаций A L h ( t ).

Работа выполнена при частичной финансовой поддержке РФФИ, проект 14-01-00102.