Динамический расчет многоэтажного каркасного здания на действие импульсов синусоидальной формы

Современные конструкции испытывают сложные динамические нагрузки эксплуатационного и специального характера в виде ударов, импульсов, групп импульсов и т.д. Однако решение задачи о действии периодических кратковременных импульсов на систему с несколькими степенями свободы при учете внутреннего трения еще в недавнем прошлом не представлялось возможным [1] и наибольшие во времени перемещения системы оценивались весьма приближенно. С развитием более совершенных методов динамического анализа можно рассматривать реальную работу конструкций с учетом принятых допущений.

Общая информация

Наиболее эффективным методом динамического расчета упруго-вязких дискретных систем является временной анализ реакции, базирующийся на алгебраических подходах. Уравнение движения дискретной диссипативной системы и его алгебраический аналог - уравнение движения собственных форм - записываются в виде [2]:

MY^ + CY^ + KY^t^PQ'), (1)

AS² + CS + ^ = 0, (2) где М= diag (m_b ..., m„), С = С^т= [c_ff], К=1?= [r_?] е Mi (Л) 0,7 = 1, и) - положительно определенные матрицы инерции, демпфирования и жесткости соответственно; Y^ - вектор искомых перемещений; Р^ - вектор заданных внешних сил; SeM„^C) - матрица внутренних динамических характеристик системы, определяющая коэффициенты демпфирования, собственные частоты и формы колебаний.

Уравнение реакции, полученное на основе анализа уравнения (2), представляется в матричной форме интеграла Дюамеля:

Y(f) = 2 Re ] Ф (t - t₀ ^М [-SK₀ + У_о ] +

+С/”1 |ф(/-т)ГР(т)^к 'о                                      .

где U = 2i-MImS (ImS - мнимая часть S); Ф(/) = еа - матричная экспонента; Уо, Уо - векторы начальных перемещений и скоростей; S - матрица, сопряженная к S.

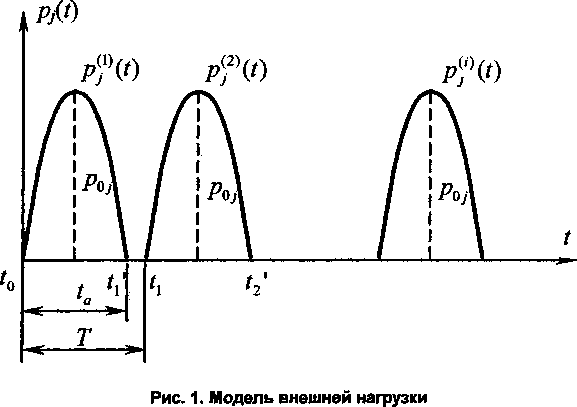
Уравнение реакции (3) является наиболее общей формой записи уравнения для динамической системы и содержит реакцию системы при свободных колебаниях (первое слагаемое в фигурных скобках) и реакцию при вынужденных колебаниях (второе слагаемое). В частности, из этого уравнения можно получить реакцию системы при действии группы периодических импульсов синусоидальной формы (рис. 1). Перемещения и скорости узлов системы на активном участке действия <-го импульса длиной t0 определяются уравнениями:

У(/) = 2Ке{ф(г-г,_₁)17-¹Л/[-§У₀ + У_о] + ^(ОР_о} -У^гКе^^-/,..!)^^ +%]+.вд), Х^ = [вФ (Г - t_M ) - s sin (6 (/-<„!))-

-0cos(e(z-7_1))][tz(52+e2)]‘1.

Здесь 0 = diag(i9l,192,...,i9„) - матрица угловых частот; tM, t/ - моменты начала и окончания действия z-го импульса.

Выражения для перемещений и скоростей системы при свободных колебаниях после окончания действия /-го импульса имеют вид:

У(0 = 2Ке{ф(/-г, ')(/-1Л/[-5У0 +У0]},

У(0 = 2Ке|5Ф(г -f; '^Л/[-5У0 +У0]} -

Численная реализация разрешающих уравнений

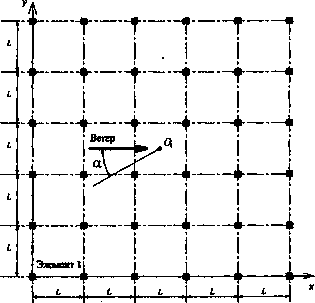
Проведен анализ колебаний 15-этажного каркасного здания постоянной жесткости при действии группы импульсов синусоидальной формы. Очертания здания в плане и общий вид представлены на рис. 2. Шаг колонн L = 6 м, высота этажа 7^= 3,3 м. Плотность материала конструкций 2,2 т/м³; модуль упругости 2,05-10⁷ кН/м². Система имеет 3x15 = 45 степеней свободы: два линейных и одно угловое смещение в горизонтальной плоскости каждого перекрытия.

Внешняя нагрузка в уровне перекрытия каждого этажа задается группой периодических им пульсов синусоидальной формы (см. рис. 1), которую можно представить как модель ветровой нагрузки. Амплитудное значение ветровой нагрузки определяется в соответствии со СНиП [4] (Ш-й ветровой район, тип местности А) и меняется в зависимости от этажа в пределах Рх - 28,215 кН до Р15 =63,954 кН.

Внешние динамические параметры системы (матрицы инерции, жесткости и демпфирования) определяются приложении, разработанном на базе программного комплекса Matlab. Матрица демпфирования соответствует модели непропорционального демпфирования и определяется по формуле [2]: С = КТ , где Г = diag(tj,/₂,..., г„),

Рис. 2. Общий вид здания, план этажа

/; = — — , 5 - логарифмический декремент \ ги колебаний; т,, rh - диагональные элементы матриц инерции и жесткости. Поскольку такая матрица демпфирования не является симметричной, необходимо преобразовать уравнение (1), умножив его справа на матрицу К-ХМ . В результате получим уравнение симметричными матрицами-коэффициентами:

МК"^ХМ У (t) + ТМ У (t) + АГУ (?) = Р^К~^ХМ ■

Внутренние динамические параметры системы (матрицы коэффициентов демпфирования, собственных форм колебаний и собственных частот) определяются на основе матрицы S, так как они являются собственными значениями этой матрицы. Собственные частоты здания представлены в табл. 1. Вследствие симметрии здания в плане частоты, соответствующие линейным формам колебаний, дублируются.

Анализ колебаний каркаса проводился при варьировании длины импульса ta, периода его действия Тр и угла а действия нагрузки. Графики (рис. 3-5) построены при периодичности действия импульсов ТР =7^/2 = 0,76 с, где Тх =1,522 с -период основного тона колебаний каркаса.

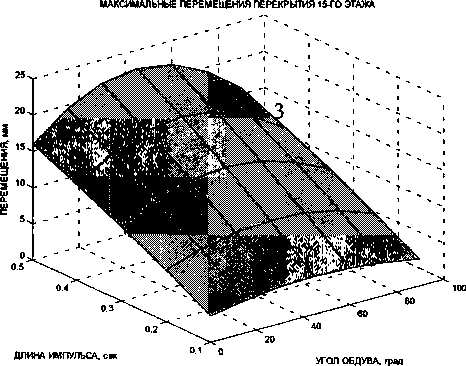
Анализ полученных поверхностей показывает, что максимальные перемещения вдоль оси х возникают в здании при а = 0°, а вдоль оси у при а = 90° ; максимальные суммарные перемещения и нормальные напряжения в колоннах возникают при а = 45°. Это не противоречит расчетам, выполненным в программном комплексе Лира, что позволяет говорить о достоверности результатов.

Максимальное суммарное перемещение 5шах=2,25 см, максимальное напряжение ^шах =4,71 МПа. С увеличением длины импульса растут перемещения и напряжения (см. рис. 3, 5). Максимальные нормальные напряжения, возникающие в колоннах различных этажей, показаны на рис. 6.

В связи с тем, что жесткость здания по высоте постоянна (рис. 7а), величина максимальных нормальных напряжений с увеличением номера этажа монотонно убывает (кривая а на рис. 6). В случае здания со ступенчато переменной жесткостью (рис. 76) в уровне этажа с измененной жесткостью наблюдается резкий скачок напряжений (кривая б, рис. 6).

Таблица 1

Спектр частот собственных колебаний здания

№ п/п	Частота, 1/с	Число повторений	№ п/п	Частота, 1/с	Число повторений	№ п/п	Частота, 1/с	Число повторений
1	4,1294	2	11	42,9182	2          .	21	74,4559	2
2	4,8862	1	12	49,6139	2	22	77,3372	2
3	12,3404	2	13	50,7841	1	23	78,6396	1
4	14,6022	1	14	55,8053	2	24	79,4225	2
5	20,4098	2	15	58,707	1	25	80,6846	2
6	24,1504	1	16	61,4383	2	26	83,7938	1
7	28,2485	2	17	66,0332	1	27	88,102	1
8	33,4258	1	18	66,4591	2	28	91,5114	1
9	35,7753	2	19	70,815	2	29	93,9788	1
10	42,3321	1	20	72,6985	1	30	95,4723	1

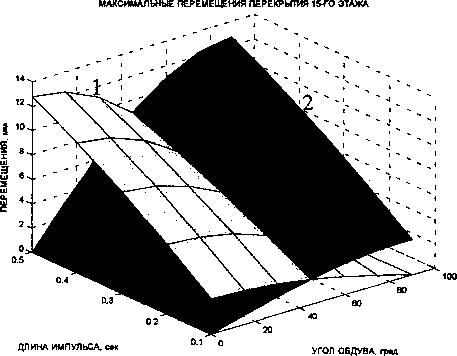
Рис. 3. Поверхности линейных смещений перекрытия 15-го этажа (1 - вдоль оси х, 2 - вдоль оси у, 3 - суммарные)

Графики (рис. 8, 9) построены при угле действия нагрузки a = 45°.

Максимальные суммарные перемещения ^тах = 6,6 см (рис. 8а) и напряжения сг^ =14,1 МПа (рис. 9а) возникают при совпадении периода внешней нагрузки ТР = 1,5 с с периодом основного тона колебаний здания Тх =1,522 с. В данном случае имеет место явление резонанса. Поскольку учитывается внутреннее трение, резонансные амплитуды являются конечными, что согласуется с известными источниками [5].

Резонанс возникает также при совпадении

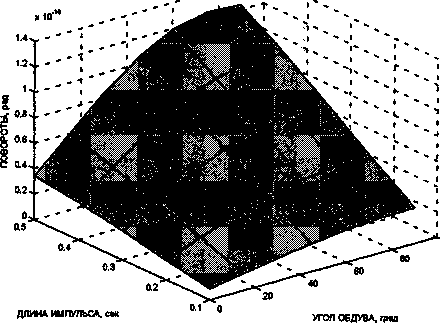
Рис. 4. Поверхность углов поворота перекрытия 15-го этажа

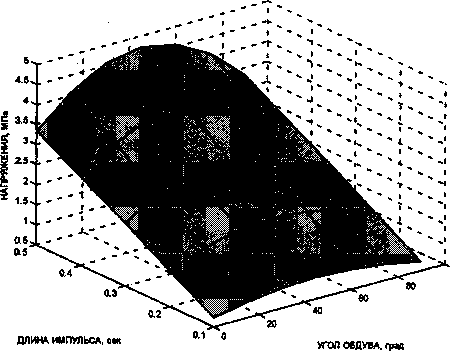
напряжений в колоннах

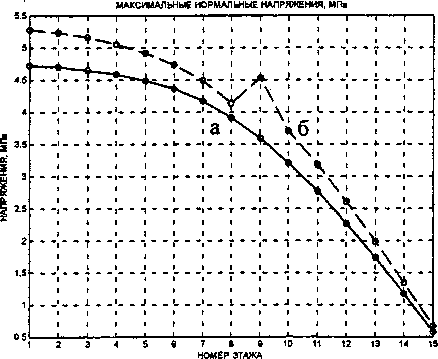
Рис. 6. Максимальные нормальные напряжения по этажам

Рис. 7. Схемы зданий: а - постоянной, б - ступенчато-переменной жесткости

Рис. 5. Поверхность максимальных нормальных

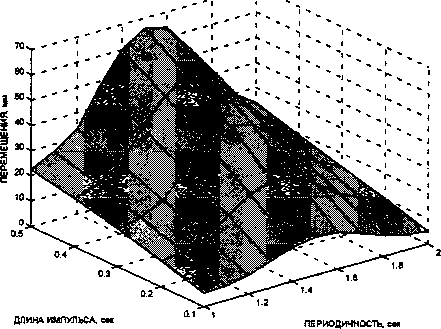
Рис. 8. Поверхности линейных смещений (а) и углов поворота (б) перекрытия 15-го этажа

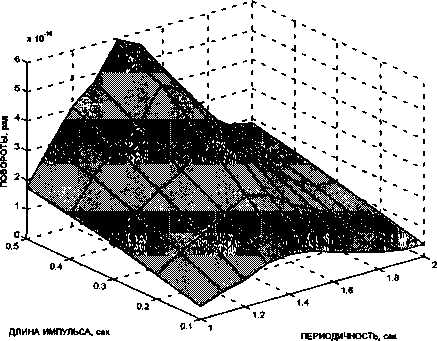
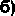
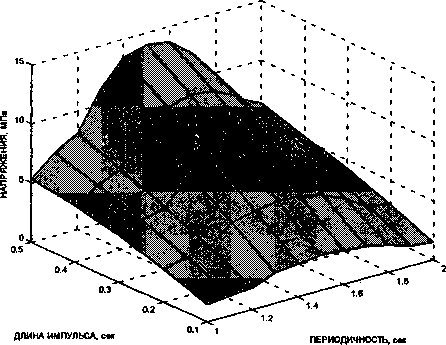
Рис. 9. Поверхности максимальных нормальных напряжений в колоннах

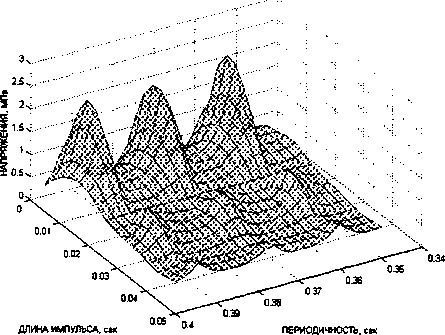
частоты внешней нагрузки с собственными частотами более высокого порядка (рис. 96).

Приведенные результаты решения динамической задачи при действии периодических импульсов с учетом внутреннего трения показывают возможность получения замкнутых решений для различных приложений динамики дискретных диссипативных конструкций. Данная методика может быть использована в традиционно трудных для анализа задачах с неустановившимися режимами колебаний, для оптимизациипроектирования строительных конструкций, поскольку отражает картину реальной работы сооружения в рамках принятых допущений.