Динамический расчет подкрановой фермы при конструктивно нелинейной работе ее элементов

Работа строительных конструкций при запро-ектных воздействиях (в виде ударов и импульсов) представляет повышенный интерес специалистов, так как это связано с проблемой надежности и безопасности сооружений, широко обсуждаемой в последнее время в научно-технической литературе [1–3].

Крановые нагрузки относятся к категории силовых воздействий и оказывают значительное влияние на конструкции производственных зданий. В соответствии с Европейскими нормами EUROCODE 1[4] эти нагрузки подразделяются на постоянные, переменные и аварийные. В зависимости от грузоподъемности крана сосредоточенная сила от колеса на подкрановую конструкцию (балку или ферму) может достигать 1000 кН и более.

Аварийные воздействия, возникающие при работе крана, могут создаваться от удара крана о тупиковые упоры либо при его наезде с грузозахватным устройством на препятствие. Кроме того, возможны аварийные ситуации, связанные с разгибом крюка или разрывом стропа, приводящие к падению груза при движении крана. В последнем случае вертикальная нагрузка на колесо крана имеет вид импульсных сил, амплитуда которых вследствие динамического характера воздействия может превышать статический эффект в 2–3 раза.

В статье приведены математические модели расчета конструкции с разрушающимися связями при аварийном воздействии. Для определения динамической реакции поврежденной конструкции используется метод временного анализа, основанный на исследовании характеристического матричного квадратного уравнения и приводящий в рамках принятых моделей к замкнутому решению во временной области [5]. При этом система рассматривается как конструктивно нелинейная, поскольку при внезапном выключении несущих элементов из работы происходит изменение параметров расчетной динамической модели (РДМ) со- оружения. В отличие от статической задачи изменяются не только жесткостные, но и инерционные и демпфирующие характеристики.

Уравнение движения дискретной диссипативной системы (ДДС) с учетом действия статической нагрузки (1, а)и начальные условия (1, б) записываются так:

MY ( t ) + CY ( t ) + KY ( t ) = P ( t ) + Q , (а)

Y ( t 0 ) = Y o , Y ( t 0 ) = Y o , (б)

где M = diag ( m 1 ,..., m ), C = С Т , K = K T e M n ( R ) - матрицы масс, демпфирования и жесткости; Y ( t ), P ( t ), Q – векторы перемещений и внешней нагрузки (динамической и статической).

Характеристическое матричное квадратное уравнение для однородного ОДУ, соответствующего (1, а), представляется в виде

M i S i ² + C i S i + K i = 0 . (2)

Из этого уравнения отыскиваются два матричных корня S 1 ₂ e M n ( C ), которые позволяют определить все параметры собственных колебаний ДДС (частоты, коэффициенты демпфирования и формы колебаний) и сформировать фундаментальные решения, входящие в общий интеграл однородного ОДУ: Ф 1 ( t ) = e S , Ф ₂( t ) = Ф 1 ( t ). При решении упругой задачи матричные корни обладают свойством сопряженности.

Система разрешающих уравнений задачи с начальными условиями (1) на интервале t e [ 1 ₀; t a ]

имеет вид:

Y ( t ) = 2Re{ Z ( t )};

'Y ( t ) = 2Re{ SZ ( t )};                         (3)

Y ( t ) = 2Re{ S² Z ( t )} + M -1 [ Q + P ( t )].

'Z ( t ) = Z o ( t - t 0 ) + Z Q ( t - t 0 ) + Z p ( t - t 0 );

Z о ( t - t 0 ) =Ф ( t - t о )U -1 M_z [ - SY o + Y 0 ];

Z Q ( t - t 0 ) = [ Ф ( t - t 0 ) - e ](US ) ^{- 1} Q ;         ₍₄₎

Z P ( t - t 0 ) = { S [ Ф ( t - t 0 ) sin( 0 t 0 ) -

- E sin( 0 t )] + [ Ф ( t - t ₀) cos( 0 t ₀) -

_ - E cos( 0 t )] 0 }[ U ( S ₀ 2 + E 0 ² )] ^-1 P₀.

Здесь U = MS + S ^T M + С . Вектор Z p ( t - 1 ₀ ) записан для случая действия синусоидального импульса P ( t ) = P₀ sin(0 1 ), где Р ₀- вектор амплитуд импульсной нагрузки; 9 = п / t a - длина импульса; Е – единичная матрица. После завершения действия импульса (при t > t a ) система совершает свободные колебания, поэтому в (4) необходимо положить Z p ( t - 1 ₀ ) = 0.

На основе кинематических характеристик (4) вычисляются силовые параметры реакции – векторы восстанавливающих R ( t ), диссипативных F ( t ) и инерционных I ( t ) сил:

R ( t ) = KY ( t ) , F ( t ) = C ( t ) , I ( t ) = - M ( t ) . (5)

Далее для каждого элемента конструкции во временной области можно определить значения абсолютных и относительных деформаций, продольных сил и нормальных напряжений.

В момент времени t , когда происходит внезапное выключение несущего элемента, необходимо выполнить корректировку внешних динамических параметров РДМ конструкции. Для этого проводится решение уравнения (2) при новых значениях матриц M , С , K и в результате полученного значения матричного корня S в системе (3) формируются матрицы U и S , а также фундаментальная матрица. Вычисление полной реакции (3) проводится с учетом замены t 0 на t в компонентах реакции (4) – Z( t ). Вектор Q определяет ^ся выражением ^Q = KY s_t = KY s_t,i, где ^Y st_t , ^Y st,i ^- векторы статических перемещений системы, соответственно, в неповрежденном и поврежденном состояниях. Векторы начальных условий (1) формируются в конце предыдущего интервала времени из уравнений (3), (4) при t = t i : Y 0 = Y ( t i ), Y > = Y ( t i ).

В качестве примера рассмотрена задача колебаний подкрановой двухпролетной фермы, вызванных действием импульсной нагрузки (рис. 1). Вертикальная нагрузка моделируется обрывом стропа на тележке с грузом при движении мостового крана (рис. 2, а).

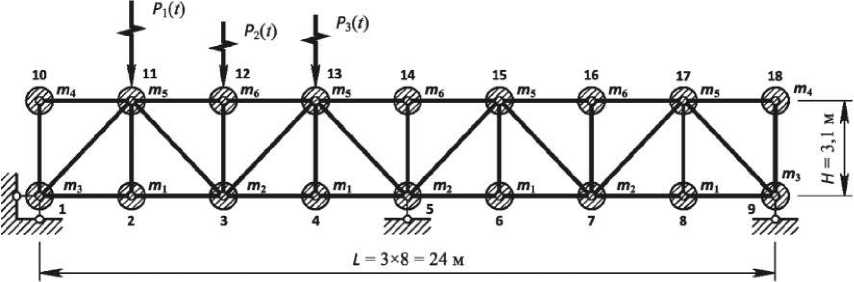
Рис. 1. Расчетная динамическая модель подкрановой фермы

В = 5,6м

2          3           4

а)

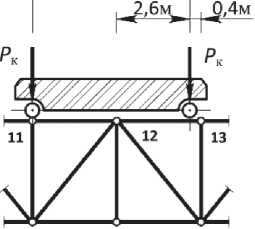
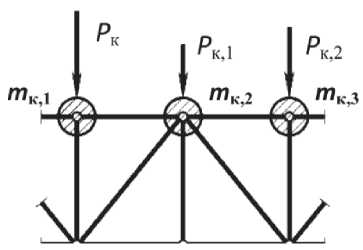
Рис. 2. Крановая нагрузка: а – положение крана в момент аварийного воздействия; б – узловая нагрузка от крана

2            3            4

б)

Каждый узел конструкции имеет две степени свободы – по горизонтали и вертикали. Общее число степеней свободы фермы, с учетом наложенных на нее связей, равно n = 32. Степень статической неопределимости – 1. Материал конструкции – сталь 09Г2 с начальным модулем упругости Е = 210060 МПа. Верхний пояс выполнен из двутавра 50Ш4, нижний пояс выполнен в виде парных уголков - 2L200 x 125 x 12, стойки -2L 125 x 12, раскосы - 2L 160 x 16. Массы m j модели складываются из масс стержней, сходящихся в узлах.

Матрица демпфирования С строится по модели непропорционального демпфирования [5, 6].

Элементы вектора статической нагрузки Q , связанные со степенями свободы в вертикальном направлении, определяются выражением Q k = M ( k , k ) g (рис. 1), где g - ускорение свободного падения тела. Элементы, относящиеся к степеням свободы в горизонтальном направлении, – нулевые. Матрица масс имеет диагональный вид, ее элементы моделируются узловыми массами, собранными с половины длины входящих в узел стержней.

Динамическая нагрузка моделируется при обрыве стропа в виде вертикальных импульсов на колесах крана, передающихся на подкрановую конструкцию. Для мостового крана грузоподъемностью 32 т со средним режимом работы амплитуда нагрузки в рабочем режиме составила Р_k = 320 кН [7]. В момент аварии самым невыгодным оказалось положение крана, представленное на рис. 2, а. Сила Рk на левом колесе тележки прикладывается к узлу 11 в полную величину, а на правом колесе пропорционально раскладывается на составляющие P_k1 = ( 0,4/3 ) Р_к и Р_{к 2} = ( 2,6/3 ) Р_к и прикладывается к двум смежным узлам 12 и 13, соответственно (рис. 2, б). При формировании матрицы масс для узлов 11-13 были учтены присоединенные (дополнительные) массы m_k, j , связанные с положением крана в момент аварийного воздействия (рис. 2, б).

При коэффициенте динамичности к _дин = 3 максимальная амплитуда нагрузки составила Р k , дин = 960 кН. Длина импульса была принята равной t_a = 0,05 с .

На рис. 3 представлены осциллограммы кинематических (а, б, в) и силовых (г, д, е) параметров реакции, вычисленные по уравнениям (3)–(5) для узлов фермы 11-13 (рис. 2).

При t1 = 0,045 с и t2 = 0,1196 с происходит выключение из работы раскосов 5-13 и 1-11, соответственно, вследствие потери устойчивости от критических сжимающих напряжений σcr = 297,7 МПа. В момент перехода системы в новое состояние (при t1) кривые перемещений и скоростей (рис. 3, а, б) являются непрерывными функциями времени, что обеспечивается постановкой началь- ных условий (1, б), причем кривые скоростей (рис. 3, б) имеют переломы. Кривые ускорений (рис. 3, в) и силовых параметров реакции (рис. 3, г–е) имеют разрывы.

На интервале t е [ t 1 ; t 2 ] резко меняется характер колебаний узлов фермы: при выключении из работы раскоса 5-13 в спектре динамической реакции наряду с основным тоном усиливается вклад высших гармоник (рис. 3).

На рис. 4 показаны осциллограммы напряжений в стержнях левого (нагруженного) пролета фермы. Пунктиром показаны кривые, относящиеся к выключаемым из работы раскосам 5-13 и 1-11.

При потере устойчивости раскоса 1-11 (при t 2 ) левая половина РДМ фермы становится геометрически изменяемой системой и, следовательно, для заданной модели с шарнирными узлами резервы прочности оказываются исчерпанными, что неизбежно приведет к прогрессирующему обрушению. Однако в силу того, что верхний пояс фермы выполнен в виде неразрезной двутавровой балки, можно считать, что данная система еще обладает некоторой несущей способностью. Расчетная модель поврежденной конструкции в этом случае представляется в виде комбинированной системы, состоящей из балки жесткости и неполной шарнирной цепи (так как часть элементов решетки и нижнего пояса выключена из работы).

Для балочного механизма разрушения с пластическим шарниром в узле 11 предельная нагрузка составила Р_u = 460 кН, что значительно ниже (более чем в 2 раза) амплитудного значения нагрузки при аварийном воздействии P_k , дин = 960 кН. Следовательно, данное запроектное воздействие приведет к полному обрушению левой части подкрановой конструкции.

Для оценки точности решения динамической задачи (1) была выполнена подстановка найденных вектор-функций кинематических параметров (3) в левую часть уравнения движения (1, а). Осциллограммы невязок этого уравнения на рис. 5 показывают, что погрешность вычислений не превышает величины A p ( t ) <  |3,6 - 10 ¹⁰| кН. Данный результат позволяет сделать предположение о том, что полученное решение является точным.

Сравнение с напряжениями по методикам [8, 9] показывает, что эти методики в целом дают завышенный результат: наибольшие отличия достигнуты для стержней 3-4 (расхождение в 5,85 раз) и 13-14 (расхождение в 8 раз) и для большинства стержней эти напряжения превышают предел прочности материала на растяжение (σ _u,t = 305 МПа) и критические сжимающие напряжения (σcr = 282...315 МПа).

Все вычисления и подготовка графических материалов выполнялись с использованием системы инженерных и научных расчетов MATLAB.

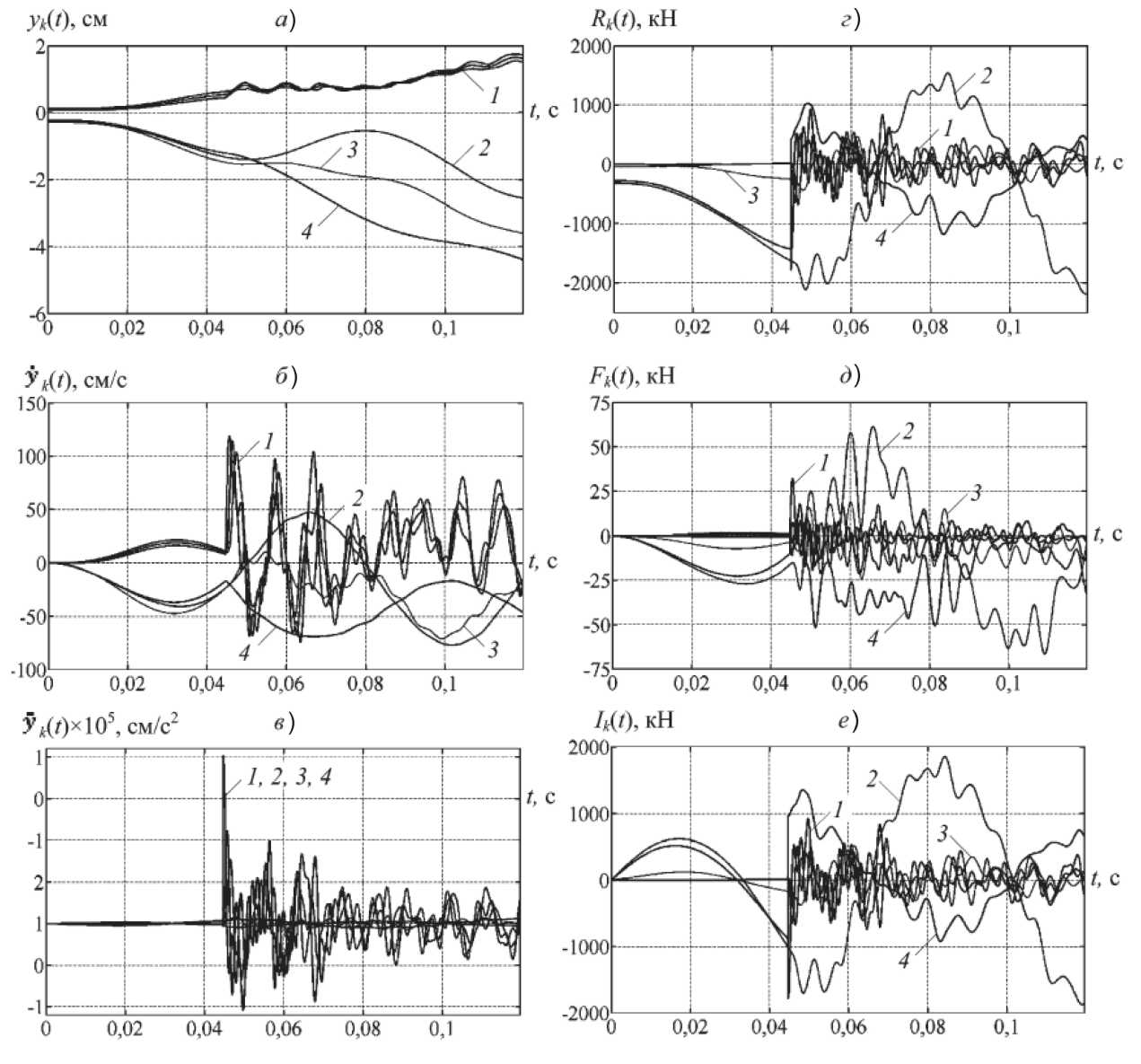
Рис. 3. Осциллограммы параметров реакции: а – перемещений; б – скоростей; в – ускорений; г – восстанавливающих сил; д – диссипативных сил; е – инерционных сил

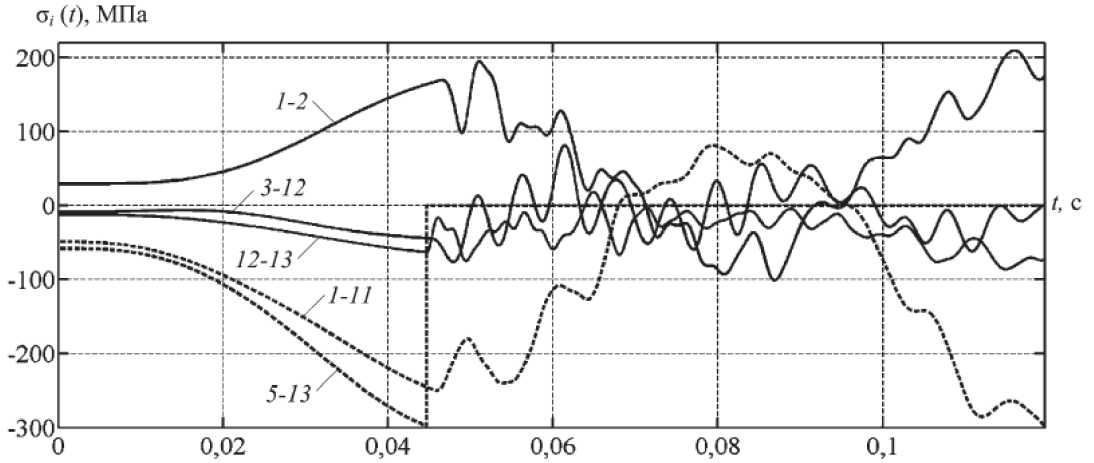
Рис. 4. Осциллограммы сжимающих и растягивающих напряжений

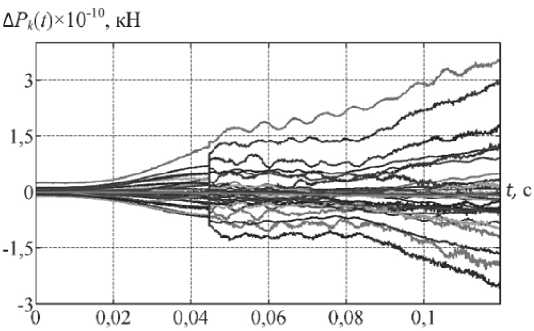
Рис. 5. Невязка уравнения движения (1, а)

Выводы. В аналитической форме построены уравнения динамической реакции ДДС с выключающимися (разрушающимися) связями. Представленные уравнения в рамках принятых моделей имеют замкнутую форму. Это подтверждает пример расчета подкрановой фермы на аварийное воздействие с выключающимися раскосами. Полученные результаты позволяют давать оценку несущей способности конструкции при отказе одного или нескольких последовательно выключающихся несущих элементов в процессе временного анализа. Открывается возможность для прогнозирования состояния конструкции в плане ее живучести, а также надежной и безопасной работы.