Динамическое деформационное взаимодействие элементов системы "ударник-прокладка-железобетонная балка"

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2018PNRPU MECHANICS BULLETIN

Железобетон – один из основных конструкционных материалов, используемых для создания современных строительных конструкций. Безопасность эксплуатации конструкций из железобетона во многом определяется их деформационным состоянием. В настоящее время для обеспечения деформационной безопасности конструкций используются автоматизированные системы мониторинга [1–6].

Как правило, в этих системах содержатся экспериментальные средства, поставляющие информацию, из анализа которой производится оценка деформационного состояния конструкции. При этом особенно важным качеством системы мониторинга является ее способность улавливать появление предкритических и критических процессов в элементах инспектируемой конструкции, а также прогнозировать возможность безопасной эксплуатации конструкции [7–9]. Такими средствами, поставляющими исходную мониторинговую информацию, в частности, могут быть разнообразные системы датчиков, регистрирующих такие деформационные параметры, как компоненты тензора деформации в локальных точках конструкции, перемещения и углы поворота элементов конструкции в характерных местах, распределение вертикальных осадок фундаментов и т.д. [10–

• 16] . Эти измерения, как правило, осуществляются в ква-зистатическом режиме. На основе математической обработки этих данных и математического моделирования деформационных процессов с использованием этих данных осуществляется анализ критичности деформационного состояния всей конструкции [17].

В настоящее время системы деформационного контроля часто дополняются средствами, позволяющими оценивать состояние конструкции на основе вибрационных измерений. К таким средствам следует отнести системы регистрация акустической эмиссии [18, 19], а также методы ударно-волновой (вибрационной) диагностики [20–23]. Вибрационная диагностика позволяет выявить наличие дефектов в конструкции и их локализацию, а также оперативно отслеживать их развитие [24–26]. Информативность этих средств с точки зрения возможности оценки появления зарождающихся необратимых повреждений в локальных местах конструкции достаточно велика. Их использование расширяется в связи с совершенствованием аппаратной (приборной) базы, позволяющей осуществлять регистрацию параметров вибрационных процессов, возникающих в наблюдаемой конструкции. Очень важной составляющей, обеспечивающей эффективность этих средств, является математический аппарат, обеспечивающий адекватную интерпретацию измеряемых вибрационных параметров [28–29].

Результаты, представленные в данной статье, относятся к ударно-волновой вибродиагностике железобетонных конструкций. Речь идет о вибрационной диагностике в «щадящем режиме», который предполагает, что воздействие на конструкцию в процессе диагностики не вызывает неупругого деформирования в элементах инспектируемой конструкции [31–33].

Такой вариант вибродиагностики в системе деформационного мониторинга реализуется следующим образом. В определенных местах железобетонной конструкции осуществляется локальное импульсное силовое воздействие с помощью металлического ударника. Механический отклик конструкции на это воздействие регистрируется совокупностью датчиков (акселерометров, велосиметров и т.п.), расположенных в разных местах конструкции. Отклик, зарегистрированный в начальный момент установки системы мониторинга (а еще лучше – в момент начала жизненного цикла конструкции), далее сопоставляется с данными измерений, полученными в текущий момент наблюдения. В результате такого сопоставления появляется возможность оценить степень накопления необратимых дефектов и соответствующего изменения свойств материала конструкции. Как происходит это сопоставление и по каким критериям оценивается, большой вопрос, не входящий в рамки данной статьи.

Предметом настоящего исследования является установление параметров локального импульсного силового воздействия, которое вызывает в конструкции возбуждение механических колебаний желаемого спектра или возбуждает упругую волну с заранее известными характеристиками фронта. Одним из основных параметров импульсного воздействия, определяющим эти характеристики, является длительность импульса. Анализу зависимости длительности силового импульса от различных факторов и оценке возможности управлять импульсом посвящена данная статья. В ней в рамках теории упругости решается начально-краевая задача о динамическом деформационном взаимодействии элементов системы «ударник–прокладка–железобетонная балка». В численном эксперименте моделируются изменения управляющих параметров, которые могут быть реализованы в эксперименте, и оценивается изменение длительности импульса.

1.    Математическая постановка задачи и её численная реализация

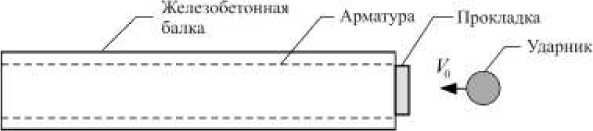
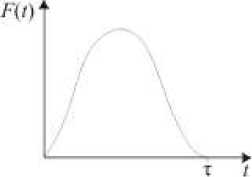
Механическое существо решаемой задачи о взаимодействии ударника, прокладки и железобетонной балки представлено на рис. 1. Неподвижная железобетонная балка через упругую прокладку деформационно взаимодействует с летящим металлическим ударником сферической формы, который в момент соприкосновения с прокладкой имеет скорость V 0 , направленную по нормали к поверхности прокладки. В процессе контактного взаимодействия ударника с прокладкой реализуется импульс силы, который инициирует ударно-волновой процесс в бетонной балке. Характерный вид силового импульса в развертке по времени представлен на рис. 1, б . Одним из основных параметров импульса является его время действия τ . Материалы всех тел считаются линейно-упругими.

Для математической постановки этой задачи используется принцип возможных перемещений [34], в котором учитывается вариация работы внутренних напряжений, поверхностных сил и сил инерции:

∫ σδε dV = ∫ p δ udS - ∫ ρ u δ UdV . (1) V S σ V

Здесь σ , ε – соответственно компоненты тензора упругих напряжений и деформаций; u – компоненты вектора перемещений; u – компоненты вектора ускорения; p – компоненты вектора поверхностных сил; ρ – плотность; V – объем взаимодействующих тел системы «ударник–прокладка–железобетонная балка»; S – поверхность, на которую действуют компоненты вектора поверхностных сил.

Численное решение вариационного уравнения (1) осуществлялось методом конечных элементов с использованием программного средства ANSYS. Для построения конечно-элементных образов использовались конечные элементы с квадратичной аппроксимацией компонент вектора перемещения, в том числе элементы, позволяющие учитывать контактное взаимодействие.

а

Рис. 1. Расчетная схема задачи ( а ) и форма силового импульса ( б )

Fig. 1. Calculation scheme ( a ) and force impulse shape ( b )

б

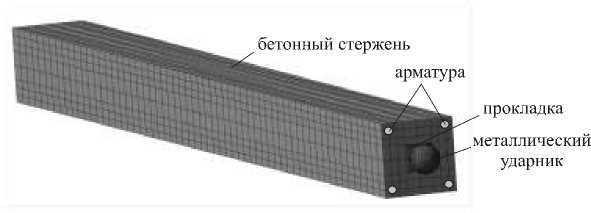
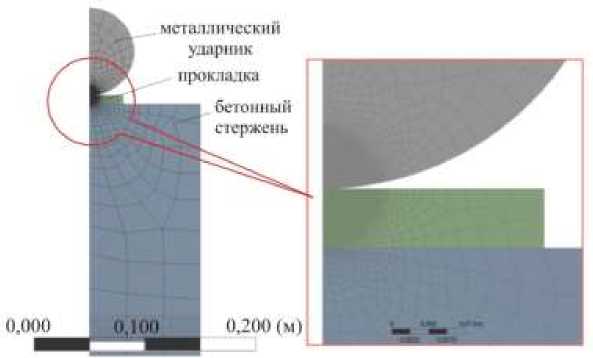
Рис. 2. Конечно-элементный образ системы «ударник – прокладка – железобетонная балка» в трехмерной ( а ) и осесимметричной ( б ) постановке

Fig. 2. Finite-element images of the «striker – gasket – reinforced concrete beam» system in three-dimensional ( a ) and axisymmetric ( b ) cases

Решение поставленной задачи о динамическом взаимодействии ударника, прокладки и железобетонной балки осуществлялось в трехмерной и осесимметричной постановке (осевая симметрия относительно продольной оси балки). В первом случае балка представляла собой призму размерами 20×20×200 см; во втором – цилиндр диаметром 20 см и длиной 200 см. В трехмерной постановке учитывалось наличие железной арматуры, тогда как в осесимметричной постановке этот фактор не учитывался и балка считалась однородным бетонным стержнем. Конечно-элементные образы элементов системы «ударник – прокладка – железобетонная балка» в трехмерной и осесиметричной постановке представлены соответственно на рис. 2. При численном моделировании структуры конечно-элементных сеток формировались неоднородными с целью наилучшей аппроксимации численного решения в областях, где напряженно-деформированное состояние может иметь большие градиенты. При решении этой задачи учитывался нестационарный динамический характер взаимодействия ударника с прокладкой. Выбранные типы конечных элементов позволили учесть изменение площади контакта поверхности деформируемого шара с поверхностью деформируемой прокладки.

Проведенные численные эксперименты с трехмерным и осесимметричным представлением взаимодей- ствующих элементов показали, что при использовании этих двух подходов моделируемый деформационный отклик балки на удар отличается незначительно, а учет металлической арматуры не сказывается принципиально на результатах расчетов. Поэтому в дальнейших расчетах балка моделировалась как однородный упругий бетонный цилиндр.

Физико-механические свойства материалов элементов балки и ударника представлены в табл. 1. Следует отметить, что модуль упругости ударника является фиксированной величиной и намного превосходит модуль упругости бетона, поэтому ударник по отношению к бетону ведет себя практически, как абсолютно твердое тело. При контактном взаимодействии его с прокладкой значимым фактором для определения длительности импульса является радиус кривизны контактирующей части ударника. Поэтому ударник можно представлять осесимметричным телом, имеющим в зоне контакта сферическую поверхность заданного радиуса кривизны. Для удобства при численной реализации ударник был представлен в виде шара. В процессе численных экспериментов механические свойства прокладки варьировались: наименьшие значения модуля упругости соответствовали резине, наибольшие – металлу. Таким образом моделировались различные материалы прокладок.

Таблица 1

Физико-механические свойства материалов

Table 1

The physical-mechanical properties of materials

Материал	ρ, кг/м3	E , ГПа	V
Бетон	2300	30·	0,2
Сталь (металлическая арматура и ударник)	7800	200	0,3
Прокладка	950	0,2–200	0,42

Использование метода конечных элементов для решения вариационного уравнения (1) позволяет получить конечномерную систему ОДУ относительно узловых неизвестных:

M • U (t)+K • U (t ) = 0, (2)

где M , K – матрицы масс и жесткости; U ( t ) – вектор узловых неизвестных как функция времени t; U ( t ) - вектор узловых ускорений. Внешнее воздействие определялось начальными условиями для компонент векторов скорости и перемещения. Для железобетонной балки и прокладки эти условия принимались нулевыми. В начальный момент соприкосновения металлического шара с прокладкой все его точки имеют скорость V 0 , направленную по нормали к поверхности прокладки, при этом компоненты вектора перемещения равны нулю.

Сходимость и достоверность получаемых решений оценивалась по величинам норм выполнения естественных краевых условий, а также по характеру сходимости численных решений в зависимости от степени дискретизации рассматриваемых областей на конечные элементы.

2.    Результаты численных решений

На основе разработанного алгоритма решения задачи о динамическом взаимодействии элементов системы «ударник – прокладка – железобетонная балка» был осуществлен ряд численных экспериментов. Основная цель этих экспериментов – установить зависимость длительности импульса силы τ (см. рис. 1, б) от различных факторов: массы ударника, радиуса ударника, скорости ударника, модуля упругости прокладки и толщины прокладки. Выбор этих пяти параметров обусловлен тем, что с их помощью можно конструктивно управлять величиной длительности импульса.

В численных экспериментах фиксировались величины четырех управляющих параметров и варьировался пятый. Выбранные базовые значения параметров и диапазоны их изменения приведены в табл. 2. Длительность силового импульса, вычисленная при базовых значениях параметров, составила S t = 1,04 мс . В табл. 2 для каждого из варьируемых параметров даны значения длительности импульса, соответствующие минимальному и максимальному значениям параметра, а также диапазон изменения длительности импульса. Графики, представляющие изменение длительности импульса при последовательном изменении каждого из управляющих параметров, приведены на рис. 3. На каждом из графиков точкой отмечена длительность импульса, полученная при базовых значениях всех пяти параметров. Выбранные пределы изменения управляющих параметров соответствуют реальным условиям проведения эксперимента.

Сопоставление полученных графиков позволяют выявить те параметры, которые позволяют наиболее эффективно воздействовать на длительность силового импульса и добиваться желаемых режимов воздействия на бетонную конструкцию. Как показал численный эксперимент, такими наиболее перспективными управляющими параметрами являются скорость ударника и материал прокладки (ее модуль упругости). Из табл. 2 видно, что в пределах выбранного диапазона изменения управляющих параметров возможно изменение длительности силового импульса от 0,25 до 2,8 мс. Это соответствует изменению частоты свободных колебаний такой системы в диапазоне от 200 до 1500 Гц.

Таблица 2

Значения управляющих параметров

Table 2

Values of control parameters

Варьируемый параметр	Базовое значение параметра	Пределы изменения параметра	Пределы изменения длительности импульса τ, мс	Диапазон изменения длительности импульса, А т, мс
Масса ударника	4 кг	0,05–10 кг	0,25–1,35	1,1
Радиус ударника	40 мм	5–140 мм	2,1–0,7	1,4
Скорость ударника	1 м/с	0,05–10 м/с	2,8–0,6	2,2
Модуль упругости прокладки	109 Па	2·107–2·1011 Па	2,5–0,5	2,0
Толщина прокладки	2 мм	0–50 мм	0,6–2,1	1,5

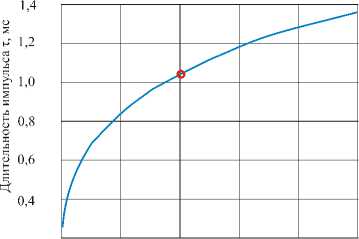
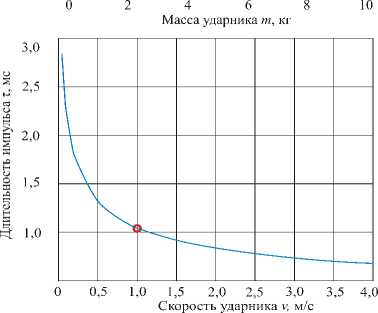
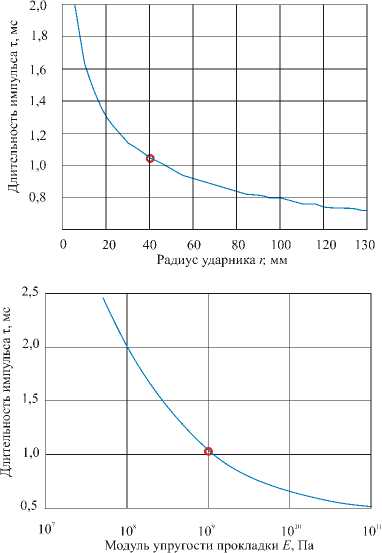
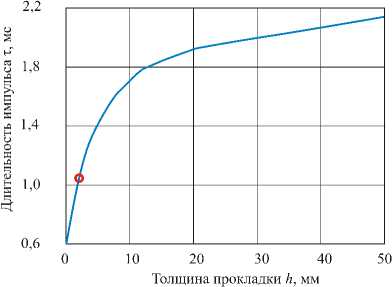
Рис. 3. Изменение длительности силового импульса при варьировании управляющих параметров

Fig. 3. The change in duration of the force impulse with varying control parameters

Заключение

Предложена математическая модель, описывающая упругое деформационное динамическое взаимодействие элементов системы «ударник – прокладка – железобетонная балка». На базе этой модели выполнен численный эксперимент, в котором анализируется длительность силового импульса, производимого воздействием сферического ударника на бетонную балку, в зависимости от ряда факторов (масса, радиус и скорость ударника, модуль упругости и толщина прокладки). Показано, что при изменении этих факторов в пределах, которые можно реализовать в физическом эксперименте, наибольший диапазон изменения длительности импульса достигается при изменении скорости ударника. Рассмотренный диапазон изменения параметров, управляющих длительностью силового импульса, обеспечивает его изменение в пределах от 0,25 до 2,8 мс. Полагая, что длительность импульса определяет одну из основных собственных частот колебаний балки, можно дать оценку для диапазона изменения частот. Он составляет от 200 до 1500 Гц.

Разработанный алгоритм позволяет достаточно быстро определить конструктивно приемлемую комбинацию факторов (масса, радиус и скорость ударника, модуль упругости и толщина прокладки), которые обеспечивают необходимый спектр волновых частот при возбуждении колебаний в железобетонной конструкции при проведении вибрационной диагностики.

Работа выполнена за счет средств Российского научного фонда (проект РНФ №14-29-00172)

Acknowledgment

The work was carried out at the expense of the Russian Science Foundation (the Project of the Russian Science Библиографический список

Foundation No. 14-29-00172).