Динамическое моделирование технических систем на Python

В рамках реализации проекта «Космическая миссия ReshUCube-3», лаборатория малых космических аппаратов (МКА) Университета Решетнева совместно с лабораторией Космических систем и технологий ФИЦ КНЦ СО РАН разрабатывает систему ориентации для малого спутника формата CubeSat 1U. Он имеет активную магнитную систему ориентации, структура которой показана на рис. 1. Она представляет собой классическую систему с обратной связью.

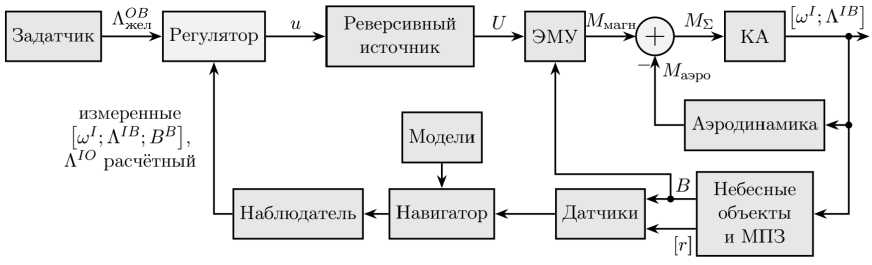
Рис. 1. Структурная схема системы ориентации КА ReshUCube-3

Fig. 1. ADCS of ReshUCube-3 structure

Состояние космического аппарата (КА) описывается угловой скоростью ω ^I и кватернионом поворота Λ ^IB связанной системы координат (верхний индекс B, body axes) относительно инерциального пространства (I, inertial). Состояние зависит от приложенного вращательного момента, который складывается из момента от аэродинамических сил M аэро и магнитного момента M магн . Управляющим является магнитный момент, который создан взаимодействием магнитных полей электромагнитного устройства (ЭМУ, магнитной катушки) и вектора B магнитного поля Земли (МПЗ).

Для управления ориентацией используется несколько систем координат – некоторые вектора просто удобнее задавать в своей системе координат. Во-первых, это связанная система координат (body axes, индекс B), оси которой связаны жёстко с аппаратом и поворачиваются вместе с ним. Обычно их располагают по строительным осям КА. Во-вторых, инерциальная система координат (inertial, индекс I), которая привязана к инерциальному пространству, к направлению на звезды. Она не вращается. В-третьих, орбитальная система координат (orbital, индекс O), всегда направленная осью z O на центр Земли (по местной вертикали), а ось x O направлена по вектору скорости КА. Эта система удобна для определения направления на Землю и учёта аэродинамических сил и моментов. Верхние индексы у вектора или кватерниона обозначают, в какой из систем координат взяты его компоненты.

Регулятор формирует сигнал управления таким образом, чтобы измеренный кватернион поворота Λ ^IB изм стал равен желаемому кватерниону Λ ^IB жел , т. е. чтобы КА встал в заданную ориентацию. По форме это классический для таких задач ПД-регулятор (для Д-канала используется угловая скорость ω ^I изм ). Отличный обзор современного состояния магнитных систем ориентации приведён в [1].

В приведённой системе управления достаточно сложными являются алгоритм навигации и алгоритм наблюдателя, которые по показаниям датчиков рассчитывают наиболее статистически достоверные значения переменных состояния КА.

В структурной схеме можно выделить группы блоков, которые имеют разную природу. Например, повороты КА, аэродинамические и магнитные моменты имеют физическую природу и действуют непрерывно; регулятор, наблюдатель и навигатор – это алгоритмы, работающие в бортовом вычислителе с некоторой периодичностью. Понятно, что при имитационном моделировании эти группы необходимо рассчитывать разными вычислительными методами, связывая их в единый расчёт, чтобы получить совместное решение.

Такой способ расчёта имеет название co-simulation, суть которого заключается в следующем. Имитационные модели частей системы объединяются со своим расчётным методом (со-лвером) – в расчётные модули. Модули последовательно, в порядке заданном структурой системы, запускаются на расчёт на некоторый шаг модельного времени. Результаты расчёта передаются в качестве начальных условий для следующих по порядку расчёта модулей. Таким образом, модули оказываются взаимосвязанными, а общее решение – совместным.

Обзор состояния проблемы

Хороший и очень детальный обзор современного состояния этой технологии приведён в [2]. Межмодульное взаимодействие обеспечивает оркестратор – некоторый менеджер модулей, задающий модельное время, определяющий очередность запуска модулей на расчёт и обеспечивающий передачу данных между модулями, от выхода к входам последующего.

ALGORITHM 3: Generic Jacobi-based orchestrator for autonomous CT co-simulation scenarios.

Data: An autonomous scenario cs = (0, Y_CS,D = (1,... ,n}, {Si} ,L,0), and a communication step size H.

Result: A co-simulation trace.

t := 0;

Xi := Xi (0) for i = 1,n;

while true do

Solve the following system for the unknowns:

( J/l = A! (t, Л?!, IZj)

....                                                                                  (15)

Уп — ^n (L x_n, u_n}

ШУ1, • ■■,Уп,Усз,и₁,...,и_л) = 6

X{ := 3i(t,Xi,Ui), for i = 1,... ,n;                            // Instruct each SU to advance t := t + H;                                                           // Advance time end

Рис. 2. Алгоритм оркестратора для систем с непрерывным временем [2]

Fig. 2. Orchestrator algorithm for continuous-time stystens [2]

На рис. 2 приведён обобщённый алгоритм оркестратора для систем с непрерывным временем. В нём явно выделен цикл по модельному времени, в котором:

• 1.    Рассчитываются выходы моделей с учётом накладываемых ограничений. Здесь решается система нелинейных уравнений, рассчитывающая рабочую точку системы.

• 2.    Рассчитываются переменные состояния моделей на следующий шаг.

• 3.    Делается шаг H по времени.

Цикл производится до достижения конечного времени.

В приведённом алгоритме λ( t , x , u ) – функция расчёта выхода модели y ; x и u – переменные состояния и входы модели; δ – функция расчёта переменных состояния системы; H – величина шага во времени; L – функционал, задающий ограничения.

Авторы [2] выделяют дискретные, непрерывные и гибридные модели в зависимости от типа взаимодействия моделей во времени. Они отличаются особенностями оркестрирования при совместном расчёте. В обзоре подробно рассмотрены проблемы совместного моделирования, специфичные для каждого типа систем, например, использование накладываемых на решения ограничений, алгебраические циклы, стратегии инициализации моделей в рабочей точке, контроль сходимости и устойчивости решения, точность и валидность связанных моделей.

На практике межмодельное взаимодействие реализуется по-разному. Обычно применяется шаблон передачи сообщений «Издатель – подписчик» [3], в котором сообщение (например, результат расчёта) помещается издателем в канал передачи данных или базу данных, а подписчик выбирает только требующиеся конкретно ему сообщения.

В некоторых реализациях издатель отправляет сообщения посреднику (брокеру). В этом случае подписчики должны регистрировать подписку у брокера, который осуществляет хранение и пересылку сообщений к подписчику. Подписчики могут подписываться на определённые сообщения на этапе написания кода, во время инициализации приложения или выполнения.

Например, хорошо документированный фреймворк HELICS (Hierarchical Engine for Large-scale Infrastructure Co-Simulation) [4] использует брокер, который организует межмодельные связи (предоставляет информацию об интерфейсах моделей), а обмен сообщениями проходит на горизонтальном уровне модель – модель, минуя брокера (рис. 3). Для подписки используются конфигурационные файлы в формате JSON, которые читаются во время инициализации. Кроме этого, в HELICS брокер несёт функцию оркестратора, синхронизируя обмен сообщениями.

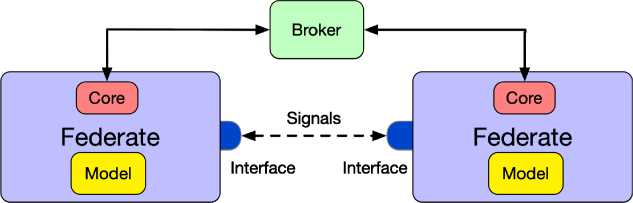
Рис. 3. Базовая архитектура фреймворка HELICS [5]. Здесь Federate – вычислительный модуль с ядром Core (управление моделированием и интерфейс сообщений) и выполняемым кодом модели

Fig. 3. Base architecture of HELICS framework [5]. Here Federate is a computational module containing a core (simulation control and message interface) and executable model code

Архитектура пакета MOSAIC, написанного полностью на Python, включает в себя ядро и набор интерфейсов (рис. 4). Ядро, в котором реализован оркестратор, состоит их двух компонент: планировщика и координатора моделей.

Пользователь пишет сценарий, который задаёт режим моделирования. На основе сценария планировщик определяет параметры моделей, обеспечивает последовательность выполнения и синхронизацию моделей, выполняет функции брокера при обмене данными. Координатор отвечает за связь между моделями, используя интерфейсы для конкретных протоколов межмодельного обмена данными.

В отечественном комплексе имитационного моделирования SimInTech брокер не используется: модель не регистрирует сигналы, а просто забирает их запросами к общей межмодельной базе данных сигналов. Архитектура комплекса приведена на рис. 5.

Комплекс SimInTech – система с компиляцией модели в машинный код, что позволяет выполнять моделирование очень быстро. Для задания собственных алгоритмов управления, содержащих сложные операции обработки сигналов датчиков и расчёта управления, используется встроенный язык программирования. Он представляет собой диалект языка Pascal, адаптированный для задач программирования имитационных моделей, работающих во времени. Например, в нем введены секции кода, выполняющиеся на отдельных этапах моделирования (компиляция, инициализация, финализация), есть возможности для обращения к системным функциям и переменным, а также для работы с базой данных сигналов моделей и ряд др.

Язык достаточно глубоко специализирован и не является полностью совместимым с языком Pascal (например, нет возможности задавать сложные типы переменных и объекты), на него нет сторонних компиляторов и отладчиков.

В последних версиях SimInTech появилась интеграция с языком программирования Python – можно разово (например, при инициализации) выполнить скрипт. Поскольку код Python не является компилируемым, при циклическом выполнении он будет выполняться достаточно долго (запуск интерпретатора, передача скрипта и параметров, выполнение, передача результатов).

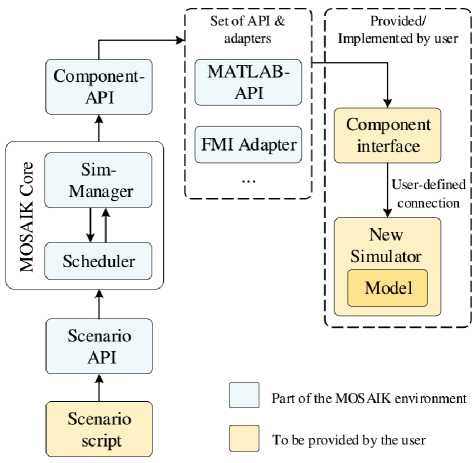
Рис. 4. Архитектура фреймворка MOSAIC [6]

Fig. 4. Architecture of MOSAIC framework [6]

Выполняется он внешним для SimInTech интерпретатором Python, а при таком способе запуска крайне сложно реализовать хранение состояния объектов (это требовалось для алгоритма SGP4, определяющего текущее положение КА [7]).

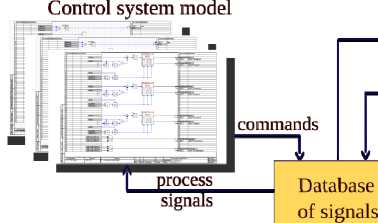
control signals process variables

Electrical model

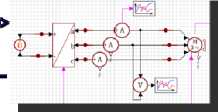
Рис. 5. Архитектура комплекса имитационного моделирования SimInTech [8]

Fig. 5. Architecture of SimInTech dynamic simulation environment [8]

Mechanical model

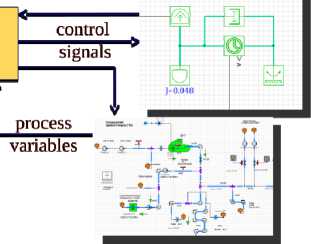
Thermohydraulical model

SimInTech позволяет разработать блок с собственными алгоритмами, используя внешние для SimInTech средства (например, в виде динамической библиотеки .dll), но процедура создания описана только для Windows, с использованием среды Delphi. В 2020 г. система SimInTech была успешно портирована на ОС Linux [9], но, к сожалению, до настоящего времени отсутствует описание процедуры создания и подключения блоков в виде динамических .so библиотек. Отладка в среде программирования SimInTech реализована не слишком удобно, хотя все основные инструменты есть (точки останова, просмотр состояния переменных и др.). Статиче- ский анализатор кода (линтер) не реализован. В результате, ряд особенностей рассмотренного выше ПО не позволил реализовать в ней модель системы ориентации; код получался достаточно громоздким, быстрорастущим и сложным в отладке.

Поэтому было принято решение переписать все алгоритмы и модели на Python, для совместного выполнения которых был написан диспетчер для совместного выполнения моделей, рассчитываемых различными алгоритмами.

Говоря о системах моделирования, реализованных с использованием Python, невозможно не упомянуть отличную и хорошо проработанную систему Basilisk [10], разработанную в центре исследования астродинамики университета Колорадо. Это компилируемая система написана на C++, а код на Python связывается (и компилируется) с системой посредством Software Interface Generator (SWIG). Соответственно, модели исполняются достаточно быстро. Basilisk написан специально для моделирования космических систем и имеет очень хорошую графическую подсистему. Также реализована возможность подключения кода на C++, реализации технологий подключения аппаратуры в контуре управления (hardware-in-the-loop), равно как и программ (software-in-the-loop). Как и все программы, обладающие большим функционалом, хорошо проработанные и имеющие долгую историю, Basilisk достаточно сложен в использовании, но эта сложность вполне себя оправдывает. Честно говоря, если бы на тот момент, когда автор начинал работу над системой ориентации, встретилась бы система Basilisk, то вряд ли была бы начата разработка собственной системы моделирования.

Полностью на Python написана модель системы ориентации, представленная в отчёте [11]. Её особенность заключается в том, что в ней используется упрощённая технология совместного моделирования: формируется общая матрица уравнений, решаемая алгоритмом LSODA для непрерывных систем на шаг по времени; затем выполняются алгоритмы системы ориентации. В системе выделены алгоритмы и уравнения отдельных блоков, каждый из которых обеспечивает формирование своей части системы уравнений.

Архитектура

На рис. 6 представлена архитектура диспетчера для имитационного моделирования систем управления.

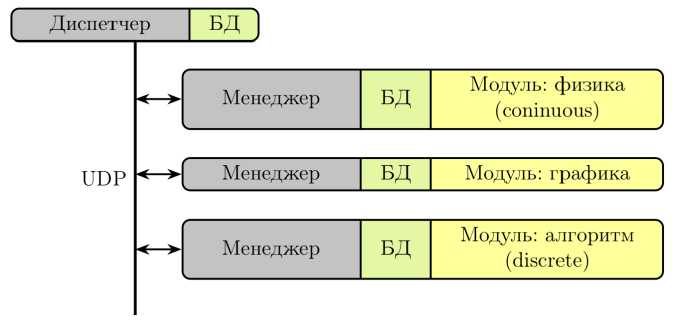
Рис. 6. Архитектура диспетчера имитационного моделирования pySimScheduler [12]

Fig. 6. Architecture of dynamic simulation model manager pySimScheduler [12]

Каждая модель реализуется в виде самостоятельного расчётного модуля. Он запускается в отдельном процессе и содержит как уравнения и алгоритмы модели, так и методы численного расчёта этих алгоритмов. Модуль должен произвести расчёт своих выходных величин на некоторый определенный интервал времени.

Подобно тому, как это реализовано в SimInTech, модуль может находиться в нескольких состояниях (рис. 7). Переход между этими состояниями происходит по командам диспетчера или в ответ на внутренние события модуля.

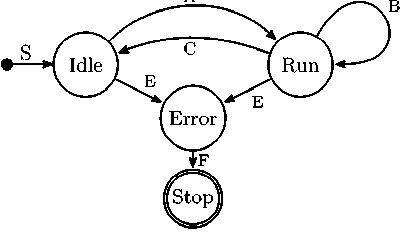
Рис. 7. Машина состояний системы pySimScheduler

После получения команды на начало моделирования, модуль переходит (A) из состояния ожидания Idle в состояние работы Run; при этом происходит инициализация графики и внутренних переменных модуля (выставляется начальное состояние). После этого диспетчер циклически выдаёт каждому расчётному модулю команду на произведение расчётного шага (B), передавая при этом модулю исходные данные (результат расчёта смежных с ним модулей) и забирая результаты расчёта (чтобы передать их последующим модулям). По окончании расчётного времени модуль переходит в состояние ожидания (C), выполняя действия для финализации расчёта (дорисовка графики, закрытие файлов). Если во время расчёта происходит внутренняя ошибка, модуль переходит в состояние ошибки (E) с выдачей сообщения об ошибке диспетчеру, а затем останавливается. При этом по команде диспетчера остальные модули переходят в состояние ожидания.

Fig. 7. State machine of pySimScheduler model manager

Обмен данными производится посредством UDP-пакетов, которые содержат требующиеся для конкретного модуля переменные из общей базы данных. Каждый модуль содержит менеджер базы данных. Он производит распаковку/запаковку пакетов и раскладывает данные по внутренним переменным класса модуля. Система сделана на основе [13], где обмен производится с оборудованием стенда, работающим подобно расчётному модулю.

База данных должна содержать собственно базу переменных, которые будут общими между модулями. Также она содержит список модулей с указанием, какие переменные участвуют в обмене (какие передаются, такие и принимаются).

После инициализации модуля в его атрибутах появится объект Manager, который является менеджером базы данных. Именно он создаст (при своей инициализации) в объекте модуля требуемые атрибуты, которые являются полями общей базы данных – они будут синхронизироваться каждый расчётный шаг.

Общая база данных, её поля, состав конкретных переменных для обмена с конкретными модулями задаются в классе-контейнере в виде атрибутов:

Листинг 1. Пример кода базы данных class DataBase():

• # --- общие переменные ---

• t = 0. # модельное время

dt = 0.25 # расчётный шаг tmax = 4. # время моделирования cmd = 0 # команда всем модулям

• # --- пользовательские переменные ---

• U = np.array([0.1, 0., 0.]) # управление

Модули вызываются в порядке следования в словаре Tasks. Например, в листинге 2 задано три модуля (Rotation, Сontrol и Plot2D), имена которых являются ключами в этом словаре:

Листинг 2. Пример определения параметров вызова модулей

Tasks = {

'Rotation':{'Keys':"""t,cmd,dt, U,L_B,B_I,Mm_B, w_B, q_IB"""},

'Control':{'Keys':['t','cmd','U','B_I','q _IB']},

'Plot2D': {'Keys':'t,cmd,dt,U,w_B,q_IB',

'Addr':('188.162.92.100', 6502), 'noAnswer':True}

Соответствующие ключам значения также являются словарями (dict). Ини имеют обязательный ключ Keys, в котором указаны поля базы данных, которыми будет осуществляться обмен с данным модулем по указанному адресу.

Если обмен данными производится с удалённой системой, то необходимо задать сетевой адрес, по которому будут отправляться пакеты с данными. В этом случае добавляется ключ Addr, значение которого должно быть кортежем и иметь вид (ip-адрес, порт).

Можно настроить обмен так, чтобы модуль не возвращал данные, а только принимал их. Это удобно, когда модуль решает вычислительно тяжелые задачи визуализации двумерных и трёхмерных графиков. Чтобы не ожидать ответа, используется флаг noAnswer.

Поскольку для получения совместного решения в каждой из моделей используются ставшие стандартными методы решения дифференциальных и других уравнений, а обмен данными производится совершенно предсказуемо, то и общее решение будет адекватным и точным. Понятно, для устойчивого решения возникает вопрос выбора длины шага обмена переменными. Он рассматривается во многих публикациях (см. обзор [2]), и при разумном подходе к выбору параметров методов решения, совместное решение будет адекватным.

Написание и выполнение моделей

Код модели выглядит как описание класса на Python, который должен иметь методы с определёнными именами, которые вызываются при переходах между состояниями. В них требуется задать расчётный код модели. Машина состояний (см. рис. 7) и менеджер базы данных реализованы в родительском классе, от которого нужно унаследовать класс с описанием модели. По коду понятно, что нужно переопределить (при необходимости) следующие методы, задав в них требуемую модельную логику:

• –    Setup – запускается один раз при создании экземпляра класса модели;

• –    Initialize – выполняется один раз при инициализации модели перед запуском на расчёт;

• – Run – расчёт модели. Запускается циклично для каждого интервала времени dt;

  – Finalize – выполняется один раз, при завершении расчёта.

На переходах в состояние ошибки (Error) и в останов (Stop) выполняются внутренние служебные методы модуля, в которые пользователю не следует вносить логику модели.

В конце файла с кодом модели нужно создать экземпляр класса и передать управление внутренней машине состояний:

Параметрами класса модели указываются:

– TaskList: список модулей Tasks;

– DB: объект общей БД;

– isSheduler: флаг, показывающий, содержит ли модуль диспетчер и запускает ли другие модули. Один из модулей должен быть ведущим, запускать все остальные и обеспечивать обмен данными. Он должен иметь флаг isSheduler=True и запускаться последним. Удобно сделать ведущим модуль, с кодом которого мы сейчас работаем;

– isRealTime: флаг, показывающий, работаем ли в реальном времени (атрибут t соответствует реальному времени). Этот режим обычно применяется при обмене данными с реальным оборудованием.

Каждый модуль нужно запустить в отдельном интерпретаторе Python, при этом в консоли отображается состояние модуля. После запуска ведущего модуля система начинает выполнять моделирование – отрабатывает машину состояний. После того, как закончилось время моделирования, ведомые модули переходят в состояние Idle и ожидают дальнейших команд. При перезапуске модель использует начальные условия, указанные в базе данных на момент Setup; начальные условия можно задать непосредственно в коде модели.

Применение

Для определения кватерниона поворота космического аппарата относительно инерциального пространства используется алгоритм навигатора.

Пусть в текущем угловом и пространственном положении КА с датчиков получен набор единичных «измеренных» векторов b , представленный в связанной системе координат. Для малого КА, имеющего ограниченный набор датчиков, это могут быть, например, направление на Солнце, Землю и вектор МПЗ.

Также для текущего пространственного положения КА расчётным образом получены те же вектора – набор «эталонных» (референсных) единичных векторов r . Они заданы в инерциальной системе отсчёта.

Требуется найти такой поворот, который совместит эталонные вектора с измеренными векторами с наименьшей ошибкой. Этот поворот и будет определять угловое положение связанной системы координат относительно инерциальной.

Расчёт эталонных векторов необходимо проводить на борту. Исходные данные для этого алгоритма – координаты КА в инерциальной системе координат, которые рассчитываются на основе параметров TLE с использованием алгоритма SGP4. Это достаточно сложный алгоритм (рис. 8), предложенный в [14] и транслированный на многие языки программирования. Для определения координат, на КА время от времени (с интервалом примерно в неделю) передаются параметры TLE. Алгоритм SGP4 достаточно ресурсоёмкий, и поэтому точный расчет производится периодически (сутки), а между его вызовами рассчитывается приближенное, экстраполированное решение.

В имитационной модели системы расчёт эталонных векторов требуется также для моделей датчиков. В этом случае алгоритм моделирует окружающий мир – «реальное» положение Солнца и вектор МПЗ, рассчитывая соответствующин вектора r* в инерциальной системе. На основе этих векторов, модель датчиков формирует измеренные вектора b , добавляя шум и смещение.

Если рассчитывать вектора r и r* одним и тем же алгоритмом, то они будут отличаться только добавленным шумом. Поэтому, для повышения робастности системы, решено было применить разные реализации алгоритмов: в бортовом ПО использовать код С/C++ из [7; 15], а в модели датчиков – библиотеку астродинамики OreKIT [14].

Для связывания кода на C++ с диспетчером, который написан на Python, был разработан упрощенный менеджер. Он реализует аналогичную машину состояний (см. рис. 5), вызывающую нужные процедуры для инициализации (требуется для алгоритма SGP4), расчёта на шаг по времени и финализации модели. Поскольку формат структур на Python и C++ отличается, для работы с UDP-пакетами на стороне модели применена библиотека cppystruct [17]. Она позволяет распаковывать и запаковывать UDP-пакеты в формат, принимаемый библиотекой struct (пример кода приведён в директории ex5.1 репозитория [13]). В настоящий момент код менеджера формируется вызовом специального метода диспетчера, в коде будет сформирована C++ структура с именами полей, соответствующих переменным в базе данных. Программист должен самостоятельно задать вызовы нужных процедур, передавая им данные из этой структуры и заполняя её поля после расчёта.

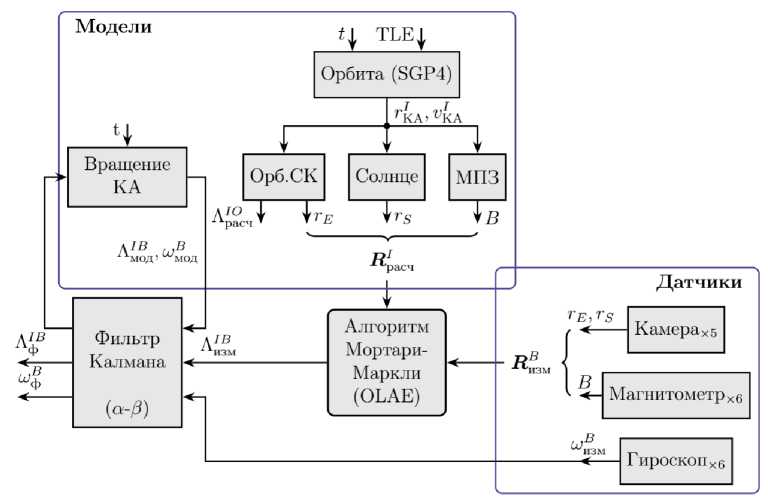
Рис. 8. Структура алгоритма навигатора

Fig. 8. Navigation algorithm structure

Управление вращательным движением КА

На рис. 9 приведена структурная схема модели вращательного движения. На ней детализированы блоки ЭМУ, КА и Аэродинамика, приведенные на рис. 1.

Управление с учётом обратной связи по аэродинамике является достаточно сложным. Детальное рассмотрение принципа управления в этом случае требует отдельной статьи. Вкратце, предварительно можно отметить, что аэродинамические моменты имеют величину порядка 10 % от моментов, создаваемых магнитной системой ориентации. Поэтому в первом приближении не будем учитывать эту обратную связь.

Вращательное движение твердого тела описывается двумя уравнениями – динамики и кинематики [16]. Первое, уравнение Эйлера, записанное в связанной системе координат (СК) в матричной форме, имеет вид

J(оB + оB х (JгоB) = MB, выражая из которого производную угловой скорости, имеем о B = J - (MB -о B х (J о B)), где J – тензор момента инерции; ωB – вектор угловой скорости; MB – вращающий момент.

Уравнение кинематики вращения, записанное в кватернионной форме, имеет вид

IB 1 IB B

Л = Л о о , где ΛIB – кватернион поворота связанной СК относительно инерциального пространства.

Момент, действующий на КА, складывается из аэродинамического и магнитного моментов. Магнитный момент используется для управления движением. Он создётся взаимодействием поля катушек L и магнитного поля Земли B. Подобно стрелке магнитного компаса, система катушек поворачивается до совпадения вектора L с полем Земли B. Вращательный момент можно рассчитать как M = L × B.

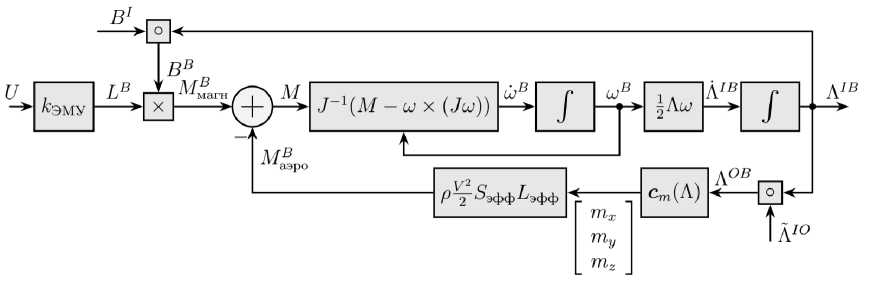
Рис. 9. Модель вращательного движения КА

• Fig. 9.    Model of satellite rotational movement

Для простоты положим, что главная обратная связь (включающая в себя алгоритмы навигации и наблюдателя) работает идеально, её коэффициент равен единице. Поэтому замкнём нашу систему и рассмотрим самый простой алгоритм, который применяется на всех (за очень редким исключением) низколетящих МКА – алгоритм гашения угловой скорости B-Dot. Он используется на начальном этапе миссии для гашения вращения, которое неизбежно возникает после выталкивания МКА из выпускного контейнера ракеты-носителя.

Классический алгоритм B-dot имеет вид [21]

M=-k i BB i, где k – коэффициент, скалярный или векторный (для случая, например, большой разницы моментов инерции по осям КА). Выбор коэффициента представляет собой отдельную интересную задачу (см., например, [18]), но даже ручной подбор даёт примлемое качество управления. Нормализация вектора производной магнитного поля (знаменатель) повышает стабильность коэффициента в контуре управления, хотя шум магнитометра, конечно, остаётся.

В виде кода алгоритм B-dot выглядит так же просто:

Листинг 4. Вариант реализации алгоритма B-dot kBDot = 500

def BDot(self):

""" алгоритм B-Dot по нормализованному вектору МПЗ """

Здесь объект Buf представляет собой буфер, в котором хранятся значения переменных t и B с предыдущих итераций. Они обновляются в основном алгоритме (см. примеры в репозитории проекта на GitFlic [19]).

На рис. 10 приведён переходной процесс для угловой скорости КА – компоненты угловой скорости ω ^B и вектора измеренного магнитного поля B^B , в осях связанной системы координат. Видно, как система не может погасить составляющую ω X – она совпала по направлению с вектором, а магнитная система физически не может создать момент вокруг вектора МПЗ.

При вращении наиболее энергоёмка ось КА с наибольшим моментом инерции. При работе алгоритма, когда создаётся противодействующий момент, именно эту составляющую наиболее трудно погасить. Поэтому практически всегда КА разворачивается так, что эта ось становится коллинеарной вектору магнитного поля B, что мы и наблюдаем на графиках переходного процесса по компонентам угловой скорости.

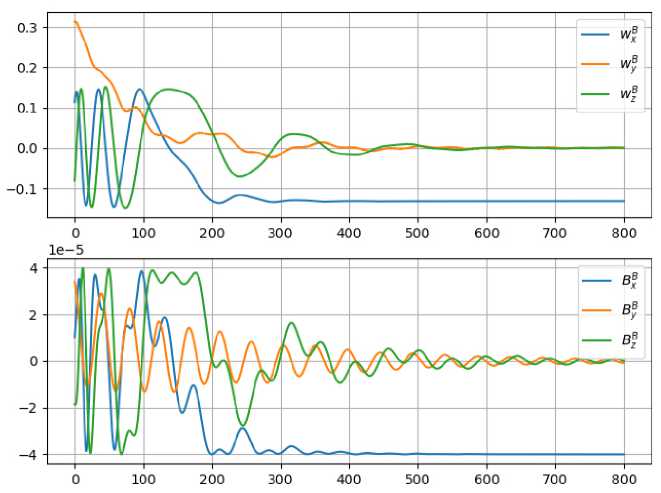
Рис. 10. Переходной процесс при гашении угловой скорости алгоритмом B-Dot

• Fig. 10.    Transient of B-Dot detumbling algorithm

Заключение

В работе представлены результаты разработки диспетчера, предназначенного для совместного выполнения имитационных моделей, составляющих многокомпонентную систему. В результате моделирования получается совместное решение переходного процесса, что позволяет проводить комплексные испытания алгоритмов и моделей. Это способствует выявлению ошибок, которые могут быть трудно обнаруживаемы при изолированном тестировании отдельных подсистем.

Особенностью разработанного программного обеспечения является реализация на популярном языке программирования Python, что позволяет бесшовно интегрировать огромное количество библиотек для Python, в том числе для разработки систем управления и анализа данных.

Обмен данными между моделями производится посредством UDP-пакетов, что позволяет использовать для написания моделей не только Python, но и другие языки программирования. По той же причине достаточно просто реализовать технологию hardware-in-loop (соответствующий пример приведён в статье [11]), что позволяет эффективнее проводить разработку систем управления.

Представлен пример применения разработанного менеджера для создания модели системы ориентации небольшого космического аппарата формата CubeSAT, имеющего магнитную систему ориентации; приведён пример реализации алгоритма B-Dot и результаты моделирования переходного процесса.

Разработанная система используется для имитационного моделирования и разработки системы ориентации аппаратов проекта «Космическая миссия ReshUCube-3».

Приведены ссылки на исходный код системы (BSD License), который выложен в открытом доступе на GitFlic [21], документация выложена на платформе ReadTheDocs [10].