Динамическое проектирование управляющего устройства гидрогенератора с учётом возмущений
Автор: Джолдошов Б.О., Сартов Т.Э., Темиркулова Н.Т.
Журнал: Огарёв-online @ogarev-online
Статья в выпуске: 15 т.5, 2017 года.
Бесплатный доступ
Рассматривается задача управления объектом в условиях неконтролируемых внешних воздействий. Целью управления является обеспечение заданных границ выходов системы автоматического управления.
Короткий адрес: https://sciup.org/147249390
IDR: 147249390 | УДК: 62-50
Текст научной статьи Динамическое проектирование управляющего устройства гидрогенератора с учётом возмущений
Введение. Проблемы эффективного управления агрегатами (и генераторами) являются весьма актуальными, чрезвычайно сложными и практически недоступными для существующих в энергетике методов и подходов автоматического управления. В настоящее время возникла необходимость в разработке новых методов и алгоритмов управления, которые обеспечивали бы надежную генерацию электроэнергии нужного качества с одновременной минимизацией ее себестоимости. Для эффективного управления гидроагрегатами необходимо рассматривать их нелинейные модели с учётом неопределенных и неконтролируемых внешних возмущений и проводить синтез и проектирование САУ (систем автоматического управления) совершенно новыми методами и алгоритмами, которые в наиболее полной мере позволят учесть явления взаимосвязанности и нелинейности процессов.
Физическую сущность многих современных технических систем, в том числе и генераторов энергосистем, составляют колебательные процессы. Колебательные режимы могут быть как полезными, так и вредными. В отношении генераторов крайне нежелательными колебательными режимами являются самораскачивание и самовозбуждение, т.к. они приводят к возникновению нарастающих незатухающих колебаний, т.е. к нарушению устойчивости. Особенно важным случаям являются внешние низкочастотные гармонические возмущения, действующие на генераторы со стороны энергосистемы. Возмущения со стороны электроэнергетической системы (ЭЭС) способствуют появлению системных колебаний, что, в свою очередь, может привести к нарушению устойчивости ЭЭС, асинхронному ходу и развитию системной аварии [1; 4].
Математическая модель объекта управления. Математическая модель гидроагрегата, работающего на систему неограниченной мощности в пространстве состояний, описывается системой нелинейных дифференциальных уравнений в виде [1; 3; 4]:
А = а\\х\ + a12x2 + ai3x3x4 + bUж sin(x5) + b^U + A;
x
x
x
= a 21 X 1 + a 22 x 2 + a 23 x 3 x 4 + b 21 U ~ sin( X 5 ) + b 22 U 1 + A 1 ;
= a31XjX4 + a32x2x4 + a33x3 + bU^ cos(x5 ) + A;= a41 (x6 + a42x1 x3 — (a43x1 + a44x2)x3 -Dx4) + A2;
S x5 = x4 - ^nom ;
x6 = 2/ T (- x6 - x7 - T (1/ Ts )(- x7 + m0 + u 2));x7 = (1 / Ts )(—x7 + m0 + u2 );
x8 = A2;x9 = s * A.
Коэффициенты дифференциального уравнения объекта управления, связанные с параметрами статора и ротора синхронного генератора [1]:
a 11 = – (r+R e ) / C; a 12 = (kM f r f ) / (L f C); a 13 = (L e – L q ) /C; b 11 = 1 / C; b 12 = kM f / (L f C);
a 21 = – kM f (R e + r) / (L d B); a 22 = – r f / B; a 23 = – kM f (L e +L q ) / (L d B); b 21 = – kM f / (L d B);
b 22 = – 1 / B; a 31 = – (L e + L q ) / L q ; a 32 = – kM f / L q ; a 33 = – (r + R e ) / L q ; b 31 = – 1 / L d ;
a 41 = 1 / H; a 42 = L q / H; a 43 = L d / H; a 44 = kM f / H; a 61 = – 2 / T ω ; a 62 = 2 / T s – 2 / T ω ;
a 62 = 2 / T s – 2 / T ω ; b 61 = – 2m 0 / T s ; b 62 = – 2 / T s ; a 71 = – 1 / T s ; a 72 = m 0 / T s ; b 72 = 1 / T s .
или
C = 0,3417; B = – 0,3627; a 11 = – 2,4926; a 12 = 9,7561 × 10-4; a 13 = – 1,0039; b 11 = 2,9268;
b 12 = 2,4390; a 21 = 2,0772; a 22 = 0,0011; a 23 = 3,4073; b 21 = 2,439; b 22 = 2,7572; a 31 = – 1,6057;
a32 = 1,3218; a33 = –0,9789; b31 = –1,1494, где:
L d = 1,3; L q = 0,87; r = 0,00165; L f = 1,38; r f = 0,0004; kM f = 1,15; H = 5; T ω = 4; T s = 1;
m 0 = 0,5; ω пот = 1; D = 1; R e = 0,85; L e = 0,527; U ∞ = 1; K = √3U ∞ .
Нелинейная вектор-функция F (x), матрица управления B, а также вектор неопределённых возмущений имеют вид:
F(x) = [ F ( x ), F ( x2),...F ( x9)] T , B = [ bn 0; b 22 0;0 0;0 0;0 0;0 b 62;0 b 72;0 0;0 0 ] ;
t = ^ ( t ) = [^;^ 2 ;0;0;0^ s -%],
F ( x ) = a^ + a12x 2 + a13x3x 4 + buUx sin( x 5), F ( x ) = a2 x + a22x2 + a23x3x 4 + b2 U sin( x 5),
F ( x ) = a.xx. + a^x. + a^x, + FU^ cos( x ,), F. ( x ) = a. .( x , + a,.xx - ( a,.x, + a^x. ) x, - Dx, ),
3 3114 32 2 4 33 3 31 ^ 5 4 ' 41 6 42 13 43 1 44 2 3 4 '
F 5 ( x ) = x 4 - ^om , F 6 ( x ) = 2 / T ( - x 6 - x - T (1/ Ts )( - x , + m Q + uT )),
F 7( x ) = (1 / T s )( - x + m 0 + u 2 ), F ( x ) = 0; F 9( x ) = 0.
где: s = ( x4 - a nom )/ w nom - скольжение, переменные вектора состояния;
x = x (t ) = Id ( t ), x 3 = x3 (t ) = Iq ( t ) — токи статора по продольным и поперечным осям d , q , соответственно; x 2 = x 2 ( t ) = В ( t ) - ток возбуждение ротора; Х 4 = X 4 (t) = a(t), X 5 = x s (t) = 3(t) -частота вращения ротора и электрический угол; Х 6 = x e (t) = P t (t) - механическая мощность на валу генератора; Х 7 = Х 7 (t) = m(t) - величина открытия водяного шлюза; Х 8 = & = &(t),
Х9 = ^2 = & (t), Х9 = ^2 = &(t) - переменные состояния модели возмущений; ui = Uf = Uf (t) - напряжение возбуждения ротора (управления синхронного генератора); U2 = Ui = Ui (t) -перемещение сервопривода (управление гидротурбиной); D - демпферный коэффициент [1]. Выберем D = 1; x = [x,x2,...,x9]T = [id,if,iq,a,5,Pm,m,^,^]T - вектор переменных состояния, характеризующих токи по соответствующим обмоткам генератора .
Постановка задачи . Рассмотрим объект управления, описываемый векторноматричным дифференциальным уравнением в пространстве состояний
х ( t ) = F ( x ) + Bu ( t ) + ^ ( t ) , t e [ 1 0, tk ] , (2)
где x e R" - вектор состояния объекта; u e R m - вектор управления;
F ( x ) = { F ( x ) } e Rn - нелинейная вектор-функция; B = { b ;„} e R nm - вещественная матрица; 1 0, tk - начальный и конечный моменты управления; Rn - n - мерное векторное арифметическое пространство. Будем предполагать, что вектор возмущения ^ ( t ) не определен и не измеряется.
Требуется определить алгоритм управления u = u ( x , t ) объектом, состояния которого описываются векторным дифференциальным уравнением (2), обеспечивающим выполнение требования к качеству процессов управления:
I x i ( t )l < 6i ( t ) , i = 1, n .
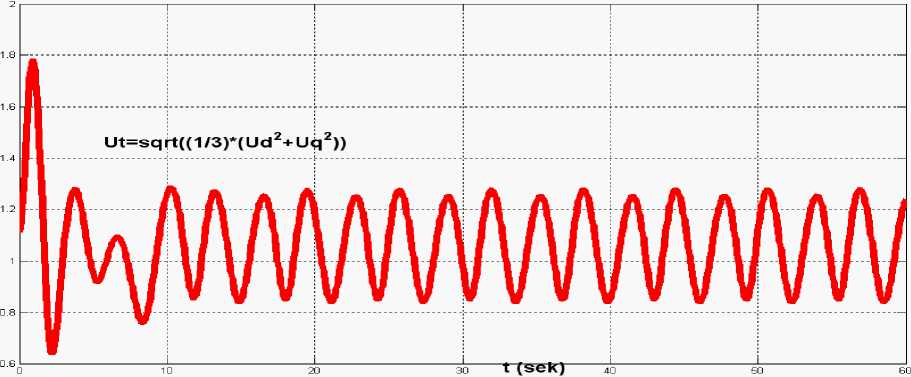
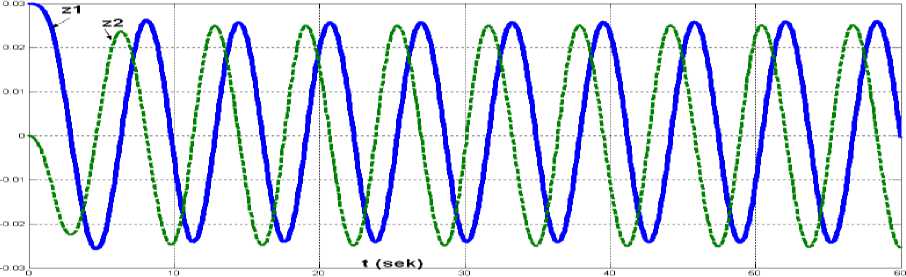
Метод синтеза САУ (построение алгоритмов управления). Решение сформулированной задачи синтеза будем осуществлять на основе подхода критерия допустимости управления [4; 5]. В соответствии с этим подходом для гарантированного обеспечения критериальных ограничений (3) достаточно выполнения неравенств tt j х;.(т)-Х.(т) dT t 0 В целях использования соотношений (4) для синтеза необходимого закона управления u (t) уравнение объекта (2) представим в координатной форме: xi(t)=Хf(x)+£biU(t)+£(t), i=1,n. i=1 С учетом уравнений (5) соотношения (4) имеют вид: t jx(T) £Fj (x)+£buue (т)+£i(T) dT < Гi(t), i to k j=1 ) = 1, n, где Г( t ) = j б(т) б.(т) dT. t0 Пусть каждая координата вектора управляющих воздействий u (t) состоит из двух частей: u( (t ) = ut (t) + U( (t), =11, m.(7) Для определения компонентов управления составим соотношения вида £f(x)+£biA=/л, i=1 n.(8) i=1M Введем обозначения m Zi(t) = £blu(t)+£i(t), i =1 n. l=1 Для определения компонентов управления u (t) положим, что Zi (t) = a-1 x(t), i = 1,n.(io) С учетом соотношений (8), (9) и (10) неравенства (6) преобразуются к виду tt Yif x (T)dT + ai JZi (T) Zi (т) < ri (t) • t0 t0 z2 (t) - z2 (t0) t z . . . 4 Можно показать, что ' (), i ( 0) = fZT)-ZiTd t0 В результате условия (11) запишутся в виде t Yf x (r) dr + ai [Z (t)-Z (t0)] < Г (t) • t 0 Определим параметры Yi, ai• Легко показать, что при касании кривой функций x (t) на верхней б( (t) и нижней —б; (t) границах, внутри которых должен находится переходный процесс x (t), должны выполняться неравенства t Y J^ (т)dT + ai [Z,2 (t)— Z,2 (t0)] < ri (t), i = 1,n, t0 что эквивалентно условиям t ai[ Zi2 (t) — Z2 (t0 )]< ri (t)— Yif ^2 (T) dT, i = 1» n. . (13) t0 Отсюда видно, что если параметры Yi выбрать так, чтобы правые части соотношений (13) принимали положительные значения, а параметры a задать так, чтобы левые части неравенств (10) были отрицательными, то условия допустимого качества управления (4) будут выполняться для всех t е[t0, tk ]• Таким образом, параметры Yi определяются из условия f б (т)-б (т) dr — Y f б2 (т) dT, i = in • (14) t0 t0 В последнем случае aii, если Zi (t)—Zi (t0 )< 0» a = i aj2 если Z2 (t) — Z2 (t0) > 0, где вещественные числа a функций Z (t) определяются как решения уравнений (10). При выбореZ (t) = 0, очевидно, что Z2 (t) > 0, что облегчает определение параметров ai. При этом необходимо, чтобы a < 0- Таким образом, выбор параметров Y, a, i = 1, n, определяет качество управления (4). Поэтому из уравнений (8) определяем первую составляющую вектора управления u s Rm : Вй (t) = y - x (t) — F (x), (15) где матрица у = diag {yi} . Отсюда получаем, что u (t) = G(у • x(t) - F(x)), где G = (BTB)-1BT. (16) Здесь предполагается, что существует обратная матрица det(B) ^ 0. Далее с учетом условий (8) и соотношений (9) имеем, что Zbu(t)+ii(t) = a-1 xi(t), i = 1, n, £=1 или в векторной форме B • u(t) = a • x(t) — i (t), i = 1, n, где матрица a = {a }. ,. Из векторного уравнения определяем закон изменения второй составляющей закона управления u (t) : u (t) = G • (a-1 • x (t) — i( t)), (17) В результате для объекта (2) вектор управления u (t) = u (t) + u (t), (18) обеспечивающий выполнение условий заданного качества замкнутой системы, определяется на основе соотношений (16) и (17). Алгоритм управления гидрогенератором. Алгоритм управления объектом (т.е. динамика синтезированного закона управления) согласно (6), (7) и (8) имеет вид: dux / dt = [ 1 / (b2 + b2 )b2 (g[ x - a x - a12x2 - ai3x3x4 - b Ucos(x5)x5) + +1/(b,2 + b,!,)b,(g^x -a^x -a..x. -a^x.x. -bU^ cos(x.)x.) + 12 22 ' 22 22 2 21 1 22 2 23 3 4 21 ^ v 5 5 z < +1/( b2 + b!2) b12 / au x+1/( b2 + b2) b12 / a x2 ], (19) du 2 / dt = [ 1 / (b62 + b72 ) b62 (g66 x6 -a 61 x6 -a62 x7 + 1 / (b62 + b72 )b72 (g77 x7 -a 71 x7 ) + + 1 / (b2 + b^2)b62 / «66x6 + 1 / (b2 + b722)b72 / «77x7 L где Ux — действующее значение напряжения. Переходные процессы САУ. Далее на рисунках 1, 2, 3, 4 приведены полученные переходные процессы САУ при следующих параметрах настройки законов управления (19): a11 =—1 g11 =—1 au = an>gn = g11; i = 2,H. . Рис. 2. Величина открытия водяного шлюза m(t) = x7(t) и механическая мощность на валу СГ Pm(t) = x6(t). Рис. 3. Напряжение на шине синхронного генератора Ut (t) Рис. 4. Переменные модели возмущений. Выводы. Разработан новый метод синтеза законов управления частотой и мощностью гидрогенератора и их групп в нелинейной постановке с учетом явлений взаимосвязанности, многомерности, нелинейности и с учетом неопределенных возмущений. На основе предложенного закона (алгоритмов) управления построены принципиально новые классы автоматических регуляторов, обеспечивающие асимптотическую устойчивость замкнутых САУ («гидрогенератор + регулятор») и инвариантность к внешним возмущениям. Регуляторы, построенные по предлагаемым подходам, существенно превосходят по своим динамическим свойствам существующие типовые регуляторы, базирующиеся на идеологии линейной теории управления. Результаты компьютерного моделирования показали эффективность построенных регуляторов. В дальнейшем внедрение регуляторов в практику управления генераторами (энергоблоков) позволит принципиально улучшить статические и динамические свойства энергосистем в аварийных и экстремальных режимах их работы.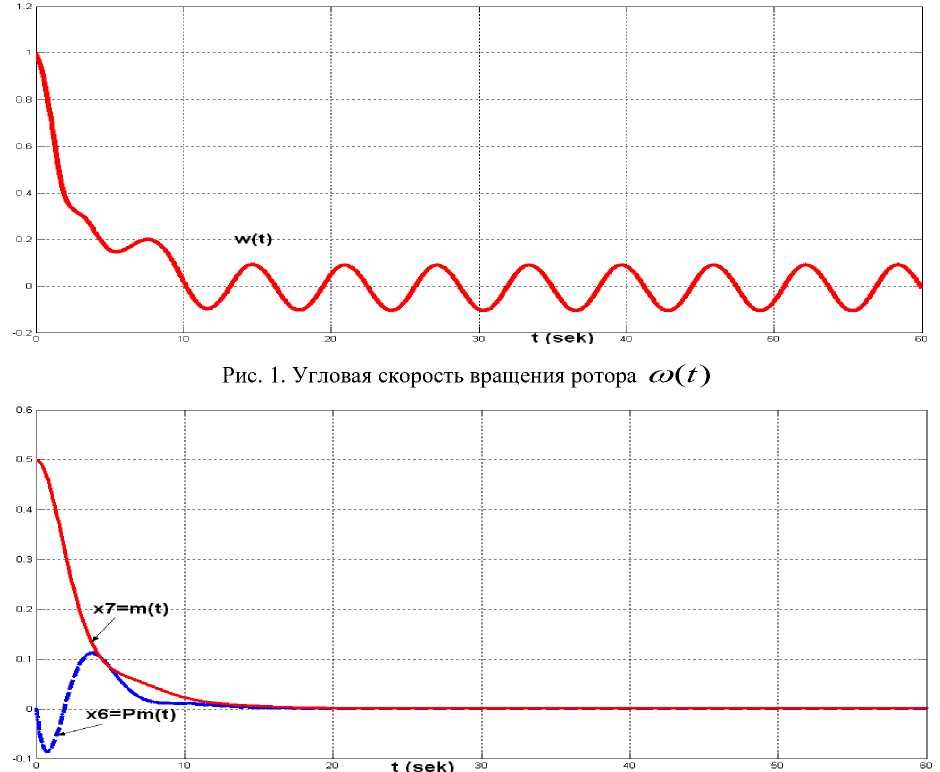
Список литературы Динамическое проектирование управляющего устройства гидрогенератора с учётом возмущений
- Андерсон П., Фуад А. Управление энергосистемами и устойчивость. - М.: Энергия, 1980. - 568 с.
- Джолдошев Б. О. Разработка методов и алгоритмов управления многомерными системами по заданным инженерным показателям качества. - Бишкек: Илим, 2011. - 166 с.
- Джолдошев Б. О., Темиркулова Н. Т. Динамическое проектирование адаптивного регулятора электроэнергетической системы // Изв. КГТУ им. И. Раззакова. - 2016. - № 39, Т. 2. - С. 87-95.
- Колесников А. А. Синергетические методы управления сложными системами: энергетические системы. - М.: Едиториал, УРСС, 2005. - 222 с. EDN: QMJBDN
- Biryukow V. F., Dzholdoshev B. O. Inequality method in a single problem of synthesis of adaptive control // Evaluation of adaptive control strategies, IFAC Workshop Series. Oxford. - 1989. - No.7. - pp. 137-142.


