Динамика атомного перепутывания в моделях с двухфотонными переходами

Современная квантовая информатика и физика квантовых вычислений базируются на перепутанных состояниях. Поэтому в настоящее время большое внимание уделяется исследованию различных схем генерации и механизмов сохранения перепутанных состояний [1]. Для практических целей квантовых вычислений пригодны лишь долгоживущие атомные перепутанные состояния. Такие перепутанные состояния наблюдались в последнее время в ряде экспериментов с ионами и атомами в магнитных и оптических ловушках [2]. Однако во многих случаях возникающие атомные перепутанные состояния оказываются нестабильными. В частности, в случае атомов, взаимодействующих с электромагнитным полем в высокодобротных резонаторах и ловушках, нестабильность атомных перепутанных состояний обусловлена осцилляциями Раби. Исчезновение квантовых корреляций между атомами за счет взаимодействия с окружением получило название мгновенной смерти перепутывания. В ряде недавних работ было показана возможность частичной стабилизации перепутывания за счет включения диполь-дипольного взаимодействия между атомами [3,4]. При этом в работе [3] исследована модель двух двухуровневых атомов с невырожденными двухфотонными переходами, взаимодействующими с двухмодовым полем в идеальном резонаторе, а в работе [4] – двухатомная модель с однофотонными переходами. Физически диполь-дипольное взаимодействие можно увеличить, уменьшая относительное расстояние между атомами в резонаторе или ионами в магнитной ловушке Пауля. Преимущество такой схемы заключается в том, что относи-

тельное расстояние между атомами или ионами можно легко контролировать. В настоящее время в современных магнитных ловушках Пауля, охлажденные атомы могут быть заперты на расстояниях порядка длины волны излучения. В этом случае параметр диполь-дипольного взаимодействия становится сравнимым с константой диполь-фотонного взаимодействия. В связи с вышесказанным, представляет интерес продолжить исследования возможности стабилизации перепутывания в системах дипольно связанных атомов. В настоящей работе нами рассмотрено влияние диполь-дипольного взаимодействия на перепутывание атомных состояний в двухатомной модели с неырожденными двухфотонными переходами рамановского типа [5].

Рассмотрим два идентичных двухуровневых атома, резонансно взаимодействующих с двухмодовым квантовым электромагнитным полем в идеальном резонаторе посредством рамановских двухфотонных переходов, при наличии прямого диполь-дипольного взаимодействия между атомами. В представлении взаимодействия и приближении вращающейся волны гамильтониан такой модели можно представить в виде:

Hi = ^ g ^ ( a + a 2 R- i + R i a 1 a + ) + ^( R 1 ⁺ R 2 + R + R ) , (1) i = 1

где a i и a j - операторы рождения и уничтожения фотонов j - ой резонаторной моды ( j = 1,2 ), R I и R i - повышающий и понижающий операторы в {- ом атоме ( i = 1,2 ), g - константа взаимодействия атомов с полем и Q -константа прямого диполь-дипольного взаимодействия атомов.

Обозначим через | +) и | -) - возбужденное и основное состояние двухуровневого атома. Тогда двухатомная волновая функция может быть представлена в виде комбинации волновых векторов вида | а, р) = | а) | р^ , где а,Р = +,- .

Рассматриваемая нами система обладает унитарной динамикой. В представлении взаимодействия такая динамика описывается оператором эволюции вида U I ( t ) = exp(- i H I t /И) . Если система, включающая атомы и поле, находится в начальный момент времени в чистом состоянии, то ее вектор состояния в любой момент времени в представлении взаимодействия может быть представлен в виде

|^( t )> - U i ( t ) |T(0)>. (2)

В двухатомном базисе | +, +>, | +,->, |-,+>, | -,-> оператор эволюции U I ( t ) для может быть записан как

' U 11 U 12 U 13 U 14 ' U 21 U 22 U 23 U 24 U 31 U 32 U 33 U 34 . ^U 41 ^U 42 ^U 43 ^U 44 ,

Матричные элементы оператора эволюции в двухатомном базисе для рассматриваемой модели могут быть представлены в виде:

AA

U_X1 = 1 + 2 a_xa ₂ ⁺ лц a ₂, U ₁₄ = 2 a_xa 2 , -^a_xa * ,

A           A

A A

U ₄₄ = 1 + 2 a ₁ a ₂ — a₁a ₂ , U ₄₁ = 2 a_xa ₂ -^a a ₂ ,

A           A

U ,2 = U 13 = a 1 a + 0 , U 21 = U 31 = 0 Ba'a 2 , U 2 ₄ = U 34 =1 Ba 1 a 2 , U 42 = U 43 = a + a 2 B ,

Y exp[-г — (a + 0) t ]

U = U = a ----²------

^{22 33}              40

{[ 1 - e^{iY 0} t ] +

i^Y (3 a +0) t        i_Y

+2 0 e ²         + 0[1 + ei ^{Y 0 t} ]},

Y exp[-i—(a + 0) t ]

U = U = a ----²------

^{23 32}              40

{[ 1 - e ^{Y 0} t ] -

i^Y (3 a +0) t         i_Y p_)t

-20 e 2       + 0[1 + eY0t ]}, где a = Q/у, A = 2(a+a2a1 a + + a1 a2+ a+ a2), 0 = ^ 8(a+a 2 a1 a 2+ + a1 a + ax+a 2) + a2

- Y^t

A = e ²

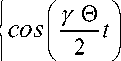
, . a . ( y 0.)' + i—sin\ ¹—t

0 I 2 ,

>

- i Y ( a+0 ) t

B = e ²

{ 1 - ee Y ^{0 t} } .

Предположим, что система “атомы+поле” приготовлена в начальный момент времени в перепутанном состоянии белловского типа

| ^(0» = [sin Ф | +, -> + cos Ф | -, +)] 11,0>, (4) где 11,0> - двухфотонное фоковское состояние резонаторного поля

Используя соотношения (1) – (4), можно представить временную волновую функцию системы в виде

|Y( t )> = X . ( t ) |+,-;1,0> +

+ X ₂( t ) |-,+;1,0> + X ₃( t ) |+,+;0,1>, (5) где

X _x ⁽ t ) = ^cosф^(U 22 ) 1,0 ^{+ sin} ф^(U 23 ) 1,0 ,

X 2 ⁽ t ) = cos ф^(U 32 ) 1,0 ^{+ sin} Ф^(U 33 ) 1,0 ,

X ₃ ( t ) = (cos ф + sin ф) —¹²⁰.

Здесь мы ввели обозначение On_x , n ₂ = ( n x , n 2 ^| O ^| n x , n 2 >>  где O - произвольный оператор, зависящий от переменных поля и | n _x, n ₂ >  - полевое состояние с определенным числом фотонов.

Информация относительно перепутывания атомов содержится в редуцированной атомной матрице плотности p_A ( t ) , которая может быть получена при усреднении полной матрицы системы “атомы+поле” p_AF ( t ) =|^( t )>(V( t ) | по переменным резонаторного поля

P a ( t ) = Tr F P af ( t ). (6)

В двуатомном базисе | +,+>, | +,->, | -,+>, | -,-> редуцированная атомная матрица плотности (6) может быть записана в виде

	2 0	0	0	0 1
	0	|X 1 |2	X 1 X ;	0
Р А =	0	X 2 X ;	X 2^	0
	0 V	0	0	|X 3 |2 ,

Для количественной оценки степени перепутывания двух двухуровневых атомов воспользуемся критерием перепутанности двух кубитов согласованностью [6]. Для редуцированной атомной матрицы плотности (6) соответствующий параметр перепутывания дается выражением

C ( P a ) = 2 max{0 , | X , X ₂ | } .     (7)

Рассмотрим также другое начальное перепутанное белловское состояние вида

| T(0)> - [sin ф | +, +> + cos ф | - , ->] |1,0). (8)

В рассматриваемом случае временная волновая функция принимает вид

| T ( t ) > = X 1 ( t ) | +, + ; 1,0 > + X 2 ( t ) | +,- ; 0,1 > +

+ X з ( t ) | -,+ ;0,1 > + X 4 ( t ) |-,- ;1,0 >, где

X 1 ( t ) = sin ф ,

X ₂ ( t ) = X ₃ ( t ) = cos ф

B 0,1

V

X ₄ ( t ) = cos ф 1 + 2

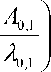
Тогда редуцированная матрица плотности может быть записана в виде

' |X 1 |² 0     0 xX

0     | X₇ |² X,X * 0

C(pA)

и, соответственно, согласованность дается выражением

C ( P a ) = 2 max{0 , | | X 1 X 4 | - | X 2 X 3 | } . (9)

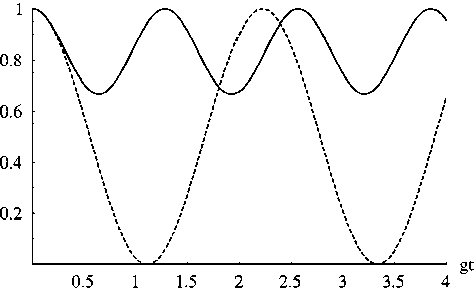
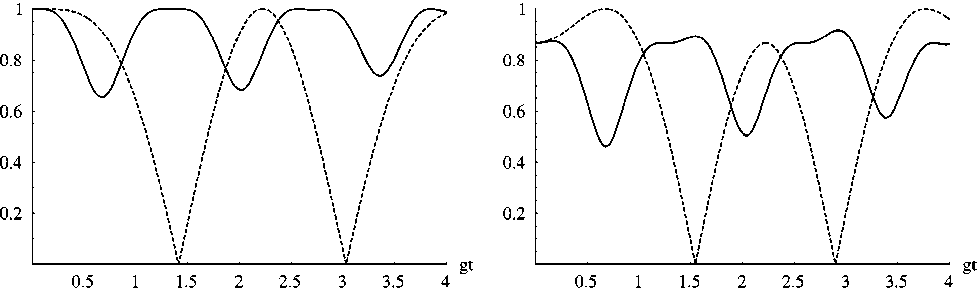
Результаты численного моделирования параметра перепутывания (7) и (9) для начальных состояний двухатомной системы вида (4) и (8) представлены на рис. 1-2. Из рисунков хорошо видно, что для рассматриваемой модели эффект мгновенной смерти перепутывания атомов отсутствует, в отличие от модели Тависа-Каммингса с невырожденными двухфотонными переходами [3]. Влияние поля на атомы проявляется в нашем случае в виде осцилляций параметра перепутывания. При этом диполь-дипольное взаимодействие приводит для всех начальных состояний и параметров модели к значительной стабилизация атомного перепутывания. Другие механизмы стабилизации перепутывания, связанные с наличием особых типов внешнего окружения, будет рассмотрены в наших следующих работах.

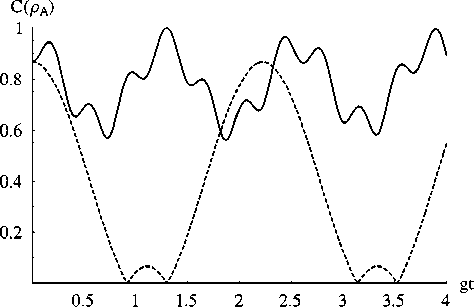
(a)                                          (б)

Рис. 1. Временная зависимость параметра перепутывания C ( p_A ) для начального состояния (4) и значений параметра ф = л /4 (а) и ф = л /6 (б). Параметр диполь-дипольного взаимодействия Q = 4 g (сплошная линия) и Q = 0 (штриховая линии)

С(Ра)                                                      С(рд)

(а)                                       (б)

Рис. 2. Временная зависимость параметра перепутывания C(р_А ) для начального состояния (9) и значений параметра ф = л /4 (а) и ф = л/6 (б). Параметр диполь-дипольного взаимодействия Q = 4 g (сплошная линия) и Q = 0 (штриховая линии

Работа выполнена в рамках Федеральной целевой программы “Научные и научно—педагогические кадры инновационной России” на 2009– 2013 годы по лоту “Проведение научных исследований коллективами научно-образовательных центров в области оптики, лазерной физики и лазерных технологий”, шифр “2010–1.1–122– 084” (номер государственного контракта 14.740.11.0063).