Динамика и моделирование транспортно-технологических машин для сельского хозяйства

Введение. Обзор работ по теме исследования [1] показал, что транспортно-технологические машины для сельского хозяйства представляют в общем виде нестационарные стохастические динамические системы с сосредоточенными и распределёнными параметрами, с голономными и неголономными связями при детерминированных и случайных возмущениях.

Ввиду отсутствия общих методов моделирования этих систем, используем метод учёта дополнительно налагаемых голономных и неголономных связей и их реакций с использованием множителей Лагранжа в качестве выходных переменных динамических систем сельскохозяйственных машин, что позволит представить уравнения движения в матрично-операторной форме или в виде графа.

Динамика и моделирование сельскохозяйственных машин. Предлагаемая форма записи уравнений движения нестационарной колебательной системы с переменными массами, конфигурация которой определяется совокупностью 5обобщённых координат qm (m = 1, 2,..., s), подчинённой г голономным нестационарным идеальным связям, описываемым уравнением F„ = = F„ (qif съ, .... qs, f) = 0 (ц = 1, 2, 3,..., г), а также г неголономным нестационарным линейным идеальным связям, описываемым уравнениями вида F. = ^avmq'm + av =0, где v = 1, 2, ..., г*; m=l оц,т av — коэффициенты, зависящие от обобщённых координат и времени, полученных из общего уравнения механики переменных масс с использованием принципа затвердевания в лагранжевых координатах, имеет вид:

F, = Yavmqm +av =o,(v=l,2,...,r ), m=l где T, П — кинетическая и потенциальная энергия системы; Ф — диссипативная функция Релея;

fm — обобщенные активные силы; \ут — обобщенные реактивные силы;---,---— частные dq dq’ производные по указанным переменным при группе переменных, принятых за независимые;

у, ^ — множители Лагранжа соответственно для голономных и неголономных связей.

В общем виде система уравнений (1) с учётом условия физической реализуемости системы в матричной форме записи для активных обобщённых сил записывается как:

W )] • [Q"(f)] + [ЖО] • [Q'(f)] + [C(f)] ■ [Q(f)] = [1(f)] ■ [f "(f)] + [ЖО] • [f'(f)] + [ЖО] • [Hf)]   (2)

где [M (f)], [/? (f)], [C (f)] — матрицы инерции, демпфирования и жёсткости системы соответственно; [1 (f)], [Р(0], [C(f)] — матрицы инерции, демпфирования и жёсткости возмущений со-

Рис. 1. Общий вид матричного уравнения движения нестационарной колебательной системы с голономными и неголономными связями в компактной форме записи (для упрощения записи аргумент времени везде опущен):

Qi, ф,..., 0s — обобщённые координаты; Xi, Х₂,..., Х_г«— неопределённые множители Лагранжа для голономных и неголономных связей (s + г = л); Ми, L^ — элементы инерционных матриц, % Р_ц„ — диссипативных матриц, Си, О_ц„ — жёсткостных матриц

Матричное уравнение (2) практически не ограничивает число входных и выходных переменных системы. Однако при очень большом числе степеней свободы колебательной системы её анализ и синтез встречают значительные трудности. В связи с этим большой практический интерес представляют вопросы упрощения колебательных систем в смысле уменьшения числа степеней свободы.

С этой целью представим колебательную систему, описываемую матричным уравнением (2), в виде графа. Для этого используем основные положения теории графов [2, 3] и их связь с матричной формой записи уравнений движения рассматриваемой колебательной системы.

Как известно, линейной или приводящейся к линейной системе соответствует сигнальный, или ориентированный, граф, отражающий причинно-следственные связи между входными и выходными переменными (сигналами) системы. Вершины (узлы) этого графа соответствуют сигналам, а соединяющие их ветви (дуги) — коэффициентам передач ветвей. Применительно к рассматриваемым колебательным системам вершинам-источникам (независимым или свободным переменным) соответствуют входные возмущения и их производные, а зависимым (базисным) вершинам (вершинам-стокам и смешанным вершинам) — выходные переменные и их производные. Смешанным вершинам инцидентны как входящие, так и исходящие ветви. Минимальное количество смешанных вершин (содержащих максимальное количество входящих и исходящих ветвей), при разрыве которых рвутся все контуры общего графа, называются существенными точками графа.

Отметим, что в зависимости от выбора существенных точек графа, для одного и того же матричного уравнения (или системы уравнений) можно построить множество равносильных графов.

Используя известные правила связи сигнальных графов с системами линейных и линеаризованных уравнений, представим колебательную систему, описываемую матричным уравнением (2) в виде графа. При этом в качестве существенных точек графа выберем вторые производные выходных переменных системы, а с целью простоты изображения исключим петли (замкнутые ветви, связывающие вершину саму с собой), то есть построим нормализованный сигнальный граф, общий вид которого представлен на рис. 2.

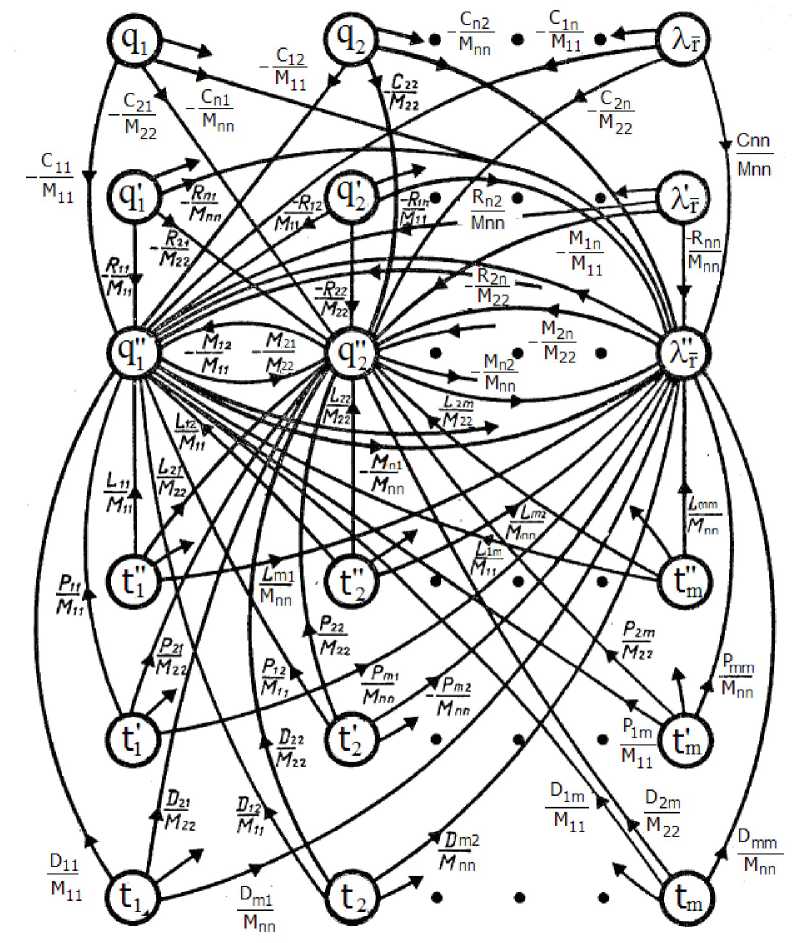
Рис. 2. Общий вид нормализованного сигнального графа нестационарной колебательной системы, матричное уравнение движения которой представлено на рис. 1

Заключение. Таким образом, математическое моделирование нестационарной динамической системы матричным уравнением типа (2) или соответствующим ему сигнальным графом позволяет решить вопросы как моделирования, так и упрощения этих колебательных систем.