Динамика ионов во фронте магнитозвуковых ударных волн
Автор: Кичигин Г.Н.
Журнал: Солнечно-земная физика @solnechno-zemnaya-fizika
Статья в выпуске: 4 т.4, 2018 года.
Бесплатный доступ
В работе рассматривается динамика ионов во фронте магнитозвуковых ударных волн (МЗУВ), движущихся под различными углами θ к вектору магнитного поля. Используется модель ударного разрыва ударной волны, в которой учитывается перепад потенциала в рампе. В результате проведенного анализа все ионы, набегающие на фронт косых МЗУВ, условно разделены на следующие категории: 1) пролетные, 2) отраженные, 3) вращающиеся перед рампом, 4) захваченные в рампе. Показано, что как вращающиеся, так и захваченные ионы присутствуют временно во фронте МЗУВ с любыми углами θ. В итоге и те и другие оказываются в строго поперечной МЗУВ пролетными, а в косых МЗУВ - либо пролетными, либо отраженными. Найден критический угол θ*, который в косых МЗУВ разделяет ионы на пролетные и отраженные. Угол θ * зависит как от скорости налетающих на рамп частиц, так и от пространственного размера перепада потенциала в рампе. Cамые важные результаты, полученные при изучении динамики отраженных ионов: 1) установлена физическая причина образования отраженных ионов, имеющих значительную энергию; 2) выявлен механизм их ускорения в рампе. В ионном форшоке околоземной ударной волны именно эти энергичные (от десятков до сотен кэВ) ионы, убегающие от ударного фронта МЗУВ под небольшим углом к плоскости фронта, проявляются в наблюдениях в виде так называемых продольных пучков (field-aligned beam - FAB) и формируют границу ионного форшока.
Ударные волны, структура фронта магнитозвуковой волны, ускорение частиц
Короткий адрес: https://sciup.org/142220305
IDR: 142220305 | УДК: 533.951 | DOI: 10.12737/szf-44201803
Текст научной статьи Динамика ионов во фронте магнитозвуковых ударных волн
В настоящее время наиболее подробно изучена структура ударного фронта квазиперпендикулярных магнитозвуковых ударных волн (МЗУВ), [Leroy, 1982; Leroy et al., 1983; Balogh, Treumann, 2013]. Схематически структуру ударного разрыва поперечной МЗУВ представляют таким образом: набегающий поток плазмы (upstream), небольшое возрастание магнитного поля — подножье (foot), область резких перепадов магнитного и электрического полей — рамп (ramp), овершут-андершут колебания (overshootundershoot oscillations) магнитного поля за рампом, плазма за ударным разрывом (downstream). В пространственной области, называемой рампом, из-за разделения зарядов образуется отражающий ионы перепад потенциала такой величины, что он может существенно затормозить налетающий на фронт МЗУВ поток ионов, за счет чего в рампе формируются резкие перепады скорости и плотности ионов. Образование подножья связывают с ионами, которые выходят из рампа, разворачиваются перед ним магнитным полем и снова попадают в рамп. Подобный разворот иона перед рампом может повторяться несколько раз, в результате чего перед рампом повышается плотность плазмы и образуется подножье [Woods, 1971], где происходит усиление магнитного поля.
В этой сложной структуре ударного разрыва МЗУВ самым существенным элементом является область рампа, где имеются скачки основных параметров плазмы: магнитного поля, потенциала, скорости и плотности. Влияние перепада магнитного поля в рампе на движение ионов не столь существенно, и в первом приближении им можно пренебречь. Это обусловлено тем, что для реальной величины магнитного поля в рампе ларморовский радиус ионов плазмы, движущихся со скоростью, близкой к скорости натекающего потока плазмы, больше или, как правило, значительно больше размера рампа d. Иногда ширина перепада потенциала порядка дебаевского радиуса, т. е. очень мала по сравнению с другими характерными для ударного разрыва масштабами. Учитывая эти обстоятельства, в существующих моделях, представляющих ударный разрыв, в рампе обычно учитывается только перепад потенциала. При этом в нулевом приближении пренебрегают перепадами магнитного поля как в рампе, так и в подножье, т. е. магнитное поле в пределах ударного разрыва считается однородным.
ИСПОЛЬЗУЕМАЯ МОДЕЛЬ УДАРНОГО ФРОНТА
И ОСНОВНЫЕ УРАВНЕНИЯ
К сожалению, в настоящее время нет строгой теории, в которой была бы рассмотрена самосогласованная картина движения частиц в плазме бесстолкновительной ударной волны (БУВ) и представлена в деталях структура БУВ. Есть результаты лабораторных экспериментов, численных расчетов и данных измерений параметров БУВ в космической плазме. Надежно установлено, что некоторые особенности структуры БУВ, например подножье, овершут и андершут, в основном контролируются движением ионной компоненты. В формировании рампа принимают участие и ионы, и электроны плазмы. В отсутствие строгой теории ударного разрыва БУВ в литературе часто используют простейшие гибридные модели БУВ, в которых отдельные структурные элементы БУВ задают «руками», а затем в рамках таких моделей анализируют динамику только ионной компоненты плазмы. В нашей работе мы тоже ограничимся таким тривиальным подходом. Несмотря на простоту, такой подход, тем не менее, позволяет получить некоторые детали структуры БУВ, которые проявляются в наблюдательных данных.
В качестве примеров мы кратко рассмотрим некоторые часто используемые модели. Большое распространение получила простейшая модель ударного разрыва, согласно которой часть ионов, налетающих на рамп, отражается от него зеркально [Woods, 1971; Gosling et al., 1982; Schwartz et al., 1983; Sckopke et al., 1983; Balogh, Treumann, 2013]. В рамках этой модели движение ионов перед рампом МЗУВ рассматривается в простейшем приближении, где предполагается следующее: 1) ионы отражаются от рампа зеркально; 2) отраженные ионы имеют скорость, равную скорости волны; 3) динамика ионов анализируется в дрейфовом приближении. Такое рассмотрение движения ионов перед рампом приводит к появлению критического угла θcr=45° [Balogh, Treumann, 2013], величина которого разделяет два раз- ных случая движения ионов перед рампом. В первом случае (θ>θcr) в некоторый момент времени ион снова попадет в рамп. Ионы, вращающиеся таким образом перед рампом, образуют подножье [Woods, 1971], которое, как считается, является отличительным признаком квазиперпендикулярной МЗУВ. Во втором случае (θ>θcr) ион, дрейфуя непрерывно вверх по течению, удаляется от рампа, поэтому нет причин для образования подножья, т. е. его нет. Мы считаем, что модель с зеркальным отражением ионов, несмотря на ее популярность, не работает, так как используемые в ней приведенные выше три предположения практически не реализуются.
Достаточно подробно изучено движение ионов еще для одной модели, в которой учтен только перепад величины магнитного поля в рампе [Alekseyev, Kropotkin,
1970;
Toptygin,
1980;
Webb et al.,
1983;
Chiueh,
1988;
Decker,
1988]
. Здесь, в предположении, что сохраняется магнитный момент частиц, показано, что при многократном пересечении рампа ионы набирают энергию за счет дрейфового ускорения. В самом благоприятном случае происходит увеличение энергии таких ионов по отношению к начальной примерно на порядок величины (см., например, [Toptygin,
1980]
). Однако учет в этой модели перепада потенциала в рампе, который, как правило, занимает небольшую долю масштаба рампа, кардинально меняет картину. Как выясняется, перепад потенциала оказывает существенное влияние на динамику ионов, в частности, на их ускорение. Например, в работе [Lever et al.,
2001]
показано, что, если пространственный размер перепада потенциала
d
ψ
меньше, чем
c/
ω
pi
, нарастание энергии ионов за счет дрейфового ускорения становится пренебрежимо малым по сравнению с ростом энергии при ускорении в электрическом поле рампа за счет серфотронного ускорения [Сагдеев,
1964;
Dawson, Katsouleas,
1983;
Ерохин и др.,
1989;
Shapiro, User,
2003;
Кичигин,
1992,
1995,
2001,
2009a]
. Согласно работам [Heppner et al.,
1978;
Balikhin et al.,
1995;
Newbury et al.,
1998;
Bale et al.,
2005;
Bale, Mozer,
2007]
, для околоземной БУВ типичное значение
d
ψ
≈
(1–5)
c/
ω
pе
, а пространственный размер перепада магнитного поля
dВ
≈(0.4–1)
c/
ω
pi
, т. е.
d
ψ
<
Таким образом, из простейших моделей наиболее адекватными являются те, в которых при анализе динамики ионной компоненты учитывается наличие в рампе перепада потенциала. В литературе наиболее часто рассматривается модель ударного разрыва, в которой заданное магнитное поле на разрыве постоянно, а заданный вручную потенциал в рампе растет линейно, т. е. электрическое поле изменяется скачком: в пределах рампа оно постоянно, а вне его равно нулю [Ohsawa, 1990; Кичигин, 1992; Lever et al., 2001; Shapiro, User, 2003]. В другой модели, более близкой к реальной, предполагается, что в рампе электрическое поле растет линейно, т. е. потенциал в пределах рампа растет с расстоянием по параболическому закону [Кичигин, 1995]. Эта модель, представленная на рис. 1, используется и в данной работе.
Ниже мы подробно рассмотрим движение ионов в пределах рампа и вне его. Учитывая полученные ниже результаты, при рассмотрении динамики ионов, движущихся в электромагнитных полях фронта, мы условно разделили ионы на следующие категории: 1) пролетные — это ионы, которые пересекают рамп либо с ходу, либо по сложной траектории и больше никогда в него не возвращаются; 2) отраженные — это ионы, которые после каких-либо простых или сложных движений во фронте МЗУВ оказываются перед рампом и удаляются от него вверх по течению; 3) вращающиеся частицы — это ионы, которые вращаются перед рампом и формируют подножье; 4) захваченные частицы — это ионы, которые в пределах рампа медленно перемещаются относительно него, поэтому длительное время находятся в рампе, медленно дрейфуя в направлении движения волны. Область перед рам-пом МЗУВ мы будем называть подножьем.
Отличительная особенность динамики захваченных частиц — они могут ускориться в рампе до значительных энергий. Акцентируем внимание на том, что как вращающиеся, так и захваченные ионы присутствуют во фронте МЗУВ временно. В итоге, как мы покажем ниже, и те и другие оказываются либо пролетными, либо отраженными.
Отраженные ионы (reflected particle component) авторы многих других статей и, в частности, обзоров [Balogh, Treumann, 2013; Wilson, 2016] называют продольными пучками (field-aligned beam — FAB).
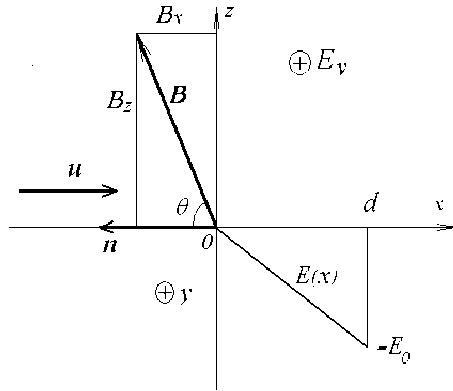
Рис. 1. Модель структуры ударной волны, представленная в системе отсчета волны. Передняя плоскость рампа — это плоскость YOZ; n — вектор нормали к рампу. Поток плазмы набегает перпендикулярно плоскости YOZ со скоростью u . Вектор магнитного поля В направлен под углом θ к нормали n и имеет компоненты Bx и Bz . Перепад потенциала сосредоточен в рампе шириной d , а электрическое поле на отрезке 0 ≤x≤d направлено навстречу набегающему потоку плазмы и линейно нарастает от нуля до амплитудного значения Е 0. Конвекционное стационарное электрическое поле Ey = uBz / с направлено вдоль оси Y (перпендикулярно плоскости рисунка)
Один из основных результатов нашей работы — это установление физических причин образования отраженных частиц, выявление механизма их ускорения в рампе и определение вида траектории движения их перед рампом МЗУВ.
Итак, цель настоящей работы — подробное исследование динамики ионов в ударном фронте, структура которого представлена моделью, схематически показанной на рис. 1. Полагаем, что МЗУВ совершает одномерное движение вдоль оси X в бесстолкновительной плазме, ионы которой имеют малый разброс по скоростям. Рассмотрение ведем в системе отсчета, связанной с рампом. Все падающие на рамп ионы разделим на две группы, в одной из которых находится основная часть ионов из потока набегающей на рамп плазмы, в другой имеется мизерная часть ионов, средняя скорость которых в системе волны почти нулевая. Как мы убедимся ниже, половина или более ионов основного потока с ходу пересекают рамп и становятся пролетными, а малая часть ионов, движущихся приблизительно со скоростью волны, может быть захвачена и ускорена электрическим полем в рампе. Полагая, что ионы основного потока налетающей на рамп плазмы почти холодные, и учитывая, что число частиц в отраженных, захваченных и других подобных группах мало, мы будем в грубом приближении рассматривать динамику ионов в этих условных группах в одночастичном приближении.
В рамках рассматриваемой упрощенной модели ударного разрыва в системе волны ион c зарядом q и массой m в окрестности фронта будет двигаться согласно уравнениям движения dvx/dt=qЕх/m+qvyBz/(mc), dvy /dt=qEy/m+q(vzBx –vxBz)/(mc), dvz/dt= –qvyBx/(mc), в которых компоненты поля во всем пространстве
Bz =Bsinθ, Bx= –Bcosθ, Ey =uBsinθ/c, где с — скорость света. Компонента Ех равна Ех= =–Е0х/d на отрезке 0≤x ≤d (в рампе) и равна нулю за пределами этого отрезка (см. рис. 1). Величина Е0 связана с амплитудой потенциала φA в волне соотношением Е0 =2φA/d. Мы анализируем динамику ионов в нерелятивистском приближении, что вполне оправдано в случае рассматриваемых нами нерелятивистских МЗУВ. К этим уравнениям добавим уравнение для кинетической энергии W=m(vx2+vy2+vz2)/2:
dW/dt=eExvx+eEy vy .
Введя обозначение ωН=qB/mc, безразмерные переменные τ=ωНt, s=vx /u, v=vy /u, w=vz /u, χ=xωН/u, η=yωН/u, ξ=zωН/u, ε=2 W//(mu2), и используя параметры
R=Е 0 /B , β =u/c , D=R/ β, ψ=2 e φ A /( mu 2), χ d= ψ /D , Ω=D/ ψ1/2, запишем уравнения движения иона в рампе в безразмерном виде:
ds/d τ =v sinθ –Ω 2χ, (1)
dv/d τ = ( 1–s )sinθ –w cosθ, (2)
dw/d τ =v cosθ. (3)
Уравнение для энергии в безразмерном виде: d ε /d τ =v sinθ –Ω 2 s χ.
Интегрируя это уравнение один раз по времени, получим закон сохранения энергии в виде
ε +Ω 2χ2/2 – ηsinθ =const .
Это соотношение использовалось нами для проверки точности численных расчетов. Параметр Ω=Е0/(Bβψ1/2) связан с наличием в рампе компоненты электрического поля Ех =–Е0х/d. Поскольку вне рампа компонента Ех отсутствует, во всех приведенных выше безразмерных уравнениях подразумевается, что вне рампа Ω=0. Уравнения (1)–(3) можно свести к уравнению для одной переменной, в качестве которой можно выбрать v или χ. Так же как для переменной v, для χ уравнение имеет вид d4χ/dτ4+(1+Ω2)d2χ/dτ2+Ω2cos2θχ=0. (4)
Приведем типичные значения используемых нами параметров, которые они принимают в околоземной МЗУВ. Рассматриваемая нами модель характерна для одномерного случая, когда поток плазмы падает перпендикулярно на переднюю плоскость рампа. Положим, что набегающая на фронт МЗУВ со скоростью
u
плазма имеет плотность
n
0
, а МЗУВ характеризуется альфвеновским числом Маха
М
А
=u/V
A
, где
V
A
=B/
(4
πn
0
т
)1/2 — альфвеновская скорость в плазме. Тогда один из важных и используемых нами параметров
D
можно представить в таком виде:
D=Е
0
/
(
B
β)
=МА
ψ(
c/
ωpi)
/d
, где ωpi
=
(4π
n
0
е
2
/т
)1/2
—
плазменная ионная частота. Для спокойного солнечного ветра
V
A
=
5∙106 см/с, его скорость набегания на околоземную ударную волну
u
≈4∙107 см/с, тепловая скорость
vТ ≈
4∙106 см/с, т. е.
vТ/u
≈0.1<<1, что позволяет считать плазму холодной. Типичные величины параметров для рассматриваемых нами МЗУВ: безразмерный потенциал ψ
≤
1, размер рампа
d
Везде ниже мы примем, что ψ = 1, и, считая набегающую на рамп плазму холодной, пренебрежем поперечными составляющими начальных скоростей ионов плазмы, т. е. положим v 0 =w 0 = 0.
РЕШЕНИЯ УРАВНЕНИЙ
ДВИЖЕНИЯ ИОНОВ ВНЕ РАМПА
В рамках нашей модели, в областях МЗУВ, находящихся вне рампа, где Ω =0, уравнения (1)–(5) решаются аналитически. При начальных условиях χ = χ r , s=sr , v=vr , w=wr решения имеют вид χ = χ r+sr τ + sinθ{[(1 –sr )sinθ –wr cosθ](τ–sinτ)+ + vr (1–cosτ)}, (5)
s=sr+ sinθ{[(1 –sr )sinθ –wr cosθ](1–cosτ)+ vr sinτ}, (6)
v=vr cosτ+[(1 –sr )sinθ –wr cosθ]sinτ, (7)
w=wr + vr cosθsinτ + [(1 –sr )sinθ –wr cosθ]cosθ(1–cosτ). (8) 26
СТРОГО ПОПЕРЕЧНАЯ МЗУВ
В этом случае движение ионов осуществляется в плоскости XOY, поэтому без ограничения общности можно положить w= 0. Как показано в работе [Кичигин, 1995] , для строго перпендикулярной МЗУВ (θ = π/2) уравнения (1)–(4), описывающие динамику ионов в рампе, решаются точно. Мы воспользуемся этими решениями, чтобы в общих чертах понять основные закономерности поведения ионов в рампе, характерные особенности которых, как мы увидим ниже, проявляются и в косых МЗУВ. Для наших целей мы используем решение для координаты и скорости ионов, налетающих на рамп с начальной скоростью s 0 :
χ=(s0–vd)sin(Ω1τ)/Ω1+vdτ, s=(s0 –vd)cos(Ω1τ)+vd, v=τ–χ.
Здесь Ω 1 = (1+ Ω 2)1/2, v d = 1/ Ω 12. Как видно из этих формул, частица в рампе в данном случае совершает движение с постоянной скоростью v d , на которое накладываются колебания с частотой Ω 1 .
Исследование приведенных решений для χ и s показывает, что на первом периоде колебаний иона его координата χ максимальна в момент времени τ m , который определяется из отношения s =( s 0 –v d )× ×cos( Ω1 τ m) +v d=0. Поскольку мы полагаем, что Ω 1≈ D >>1, v d<<1, s 0>> v d, для момента времени τ m получим оценку: τ m≈π / (2 Ω 1). Если в этот момент времени χ>χd=1 /D (χd=1 /D — безразмерная ширина рампа), ион пересекает рамп, имея значение компонент скоростей s =0, v= π /( 2 Ω 1 )– 1 /D≈ (π / 2 – 1) /D . Как следует из соотношения (5), при таких значениях скоростей s и v координата χ>0 всегда, т. е. пересекший рамп ион монотонно удаляется от него и, следовательно, становится пролетным.
Для частиц со скоростями, близкими скорости волны, s 0 ≈ 1, в момент времени τ m=π /( 2 Ω 1) координата χ ≈s 0 /Ω 1 и неравенство χ>1 /D примет вид s 0 > 1 . Отсюда следует, что с учетом малого разброса по поперечным скоростям примерно половина налетающих на рамп частиц сходу его пересекают, т. е. попадают в разряд пролетных.
Далее, анализируя выражение для χ, мы видим, что на первом периоде колебаний его значение минимально в момент времени τ = 3π / (2 Ω 1 ):
χ min =– ( s 0 –vd ) /Ω1 +3π vd/ (2 Ω 1 ).
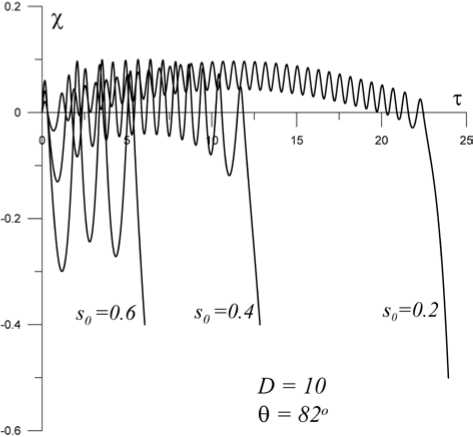
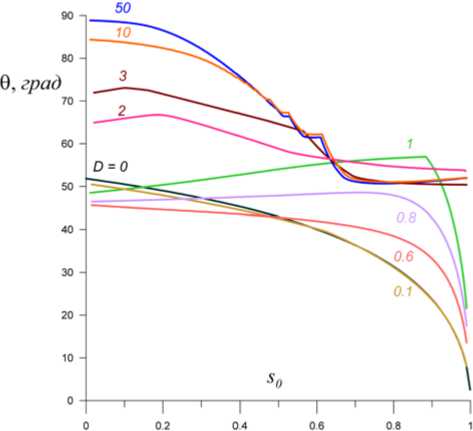
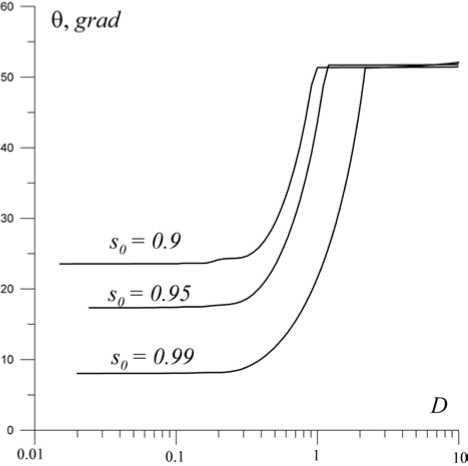
Если при этом s0 Итак, анализ решений для строго перпендикулярной МЗУВ привел нас к выводу о том, что для налетающих на рамп холодных ионов вращающиеся перед рампом частицы могут присутствовать для ограниченного интервала компонент скоростей 1>s0>vd(3π/2+1)≈6vd. Из условия s0>vd(3π/2+1) следует, что Ω12=1+Ω2>(3π/2+1)/s0 или D>[(3π/2+1)/s0–1]1/2. Таким образом, при заданном значении s0 наличие вращающихся частиц контролируется параметром D. Они появляются перед рампом только тогда, когда параметр D больше величины D=[(3π/2+1)/s0–1]1/2. При s0≈1 параметр D≈(3π/2)1/2≈2. Эта оценка подтверждается в наших расчетах. Для ионов, попадающих в область перед рампом при начальных условиях χ0=0, s= –s0, v=v0, решение для координаты иона χ примет вид χ=τ+(1+s0)sinτ+v0(1–cosτ), из которого видно, что в какой-то момент времени координата неизбежно примет положительное значение. Это означает, что любой ион, выйдя из рампа в подножье, в конце концов снова вернется в рамп. Как мы уже отметили выше, ионы, которые пересекли рамп, в него уже не возвращаются. Таким образом, в строго поперечной МЗУВ нет отраженных ионов, а все налетающие на рамп ионы в итоге становятся пролетными. КОСАЯ МЗУВ Для косых МЗУВ в двух предельных случаях, рассмотренных ниже, для движения ионов в рампе удалось найти аналитическое решение системы уравнений (1)–(3). В общем случае решение этой системы возможно только численными методами и мы, в частности, ее решали методом Рунге—Кутты. Точность расчетов контролировалась с помощью закона сохранения энергии и была не хуже 10–8. В одном частном случае, а именно, при описании динамики захваченных в рампе частиц, решение оказалось возможным, поскольку для захваченных в рампе ионов величина скорости s<<1. Учитывая этот факт, в нулевом приближении в уравнении (2) можно положить s=0, и тогда система (2), (3) имеет точное решение, которое приведено в работах [Sugihara et al., 1984; Lee et al., 1996; Кичигин, 2009а, 2009б] и имеет вид v=tgθsinτ1, (9) w=tgθ(1–cosτ1), (10) где τ1=τcosθ. Эти решения описывают колебательные движения ионов в плоскости YOZ с частотой cosθ. В следующем приближении, учитывая принятые нами неравенства s<<1, s0<<1, Ω>>1, Ω>>cosθ, подставляя полученные соотношения (9), (10) в уравнения (1), (2) и решая их, получим соотношения для координаты χ и компоненты скорости s: χ=(s0–sin2θ/Ω2)sin(Ωτ)/Ω+tgθsinθsinτ1/Ω2, (11) s=(s0–sin2θ/Ω2)cos(Ωτ)+sin2θcosτ1/Ω2. Из этих решений следует, что на колебания иона с частотой cosθ накладываются колебания с более высокой частотой Ω>>cosθ. Сравнение численных расчетов и расчетов по формуле (11) для координаты χ показало хорошее их согласие при s0<0.2. На рис. 2 демонстрируется результат такого сравнения для s0=0.1, D=10. Остановимся на анализе соотношения (11), полагая s0>sin2θ/Ω2. Во-первых, мы видим, что ион пересечет рамп, если координата χ достигнет значения 1/D, т. е. при условии tgθsinθ/Ω≈1–s0. Из этого соотношения найдем критический угол θ*, при котором ионы окажутся за рампом: θ*=arccos{D (1–s0)/2–[D2(1–s0)2/4) –1]1/2}1/2. (12) При D>>1, s0<<1 критический угол близок к значению θ*≈π/2. Ион, пересекший рамп, имеет компоненты скорости vr ≈wr≈tgθ, sr<<1 . Как следует из соотношений (5)–(8), при таких начальных значениях компонент скорости иона за рампом он становится пролетным. Если в процессе движения иона в рампе ион не преодолевает перепад потенциала в рампе, то при τ1≥π его координата станет отрицательной, т. е. ион окажется перед рампом, имея компоненты скорости sr≈vr≈0, wr=2tgθ. Движение ионов, оказавшихся перед рампом с такими начальными скоростями, подчиняется уравнениям (5)–(8), т. е. определяется соотношениями χ ≈–sin2θ(τ–sinτ), s≈–sin2θ(1–cosτ), v≈sinθsinτ, w≈2tgθ–sinθcosθ(1–cosτ). Из этих формул видно, что ионы удаляются от рампа со средней скоростью <s>≈–sin2θ, т. е. в итоге они попадают в категорию отраженных. Обратим внимание на то, что отраженные ионы имеют максимальную энергию для углов θ, близких к критическому θ*≈π/2. Эти самые энергичные ионы имеют полную скорость примерно 2tgθ* и движутся под углом α к плоскости YOZ. Угол α определяется из формулы tgα=<s>/<w>≈sin2θ*/(2tgθ*)≈sin2θ*/4≈δ/2, где δ=π/2–θ*<<1. Таким образом, отраженные ионы, Рис. 2. Зависимость координаты от времени. Красная кривая получена из численных расчетов, синяя — зависимость, полученная из формулы (11) имеющие максимальные энергии, движутся впереди ударного фронта косой МЗУВ под очень малым углом (≈δ/2) к плоскости УOZ. Как показано в работе [Кичигин, 2009б], в околоземной ударной волне предельная энергия этих энергичных ионов может достигать значений порядка 1 МэВ. Эти отраженные ионы формируют границу ионного форшока, движутся вдоль этой границы и именно они представляют популяцию продольных пучков (FAB) (см., например, обзоры [Balogh, Treumann, 2013; Wilson, 2016] и цитируемую там литературу). Как показывают результаты расчетов, приведенное выше аналитическое решение (11) можно использовать при s0<0.2. Траектории ионов при бóль-ших значениях параметра s0(0.2<s0<1) приведены на рис. 3. Видно, что с увеличением s0 сокращается время пребывания ионов в рампе и растет амплитуда их пространственных колебаний. Сокращение времени приводит к уменьшению энергии, до которой ионы ускоряются в рампе. Обратим также внимание на то, что если при малых начальных скоростях набегания ионов на рамп (s0<0.2) ионы находятся в рампе в качестве захваченных, то с увеличением s0 (s0>0.2) ионы переходят в категорию вращающихся, образуя подножье перед рампом. Напомним, что в случае строго перпендикулярной МЗУВ все частицы, налетающие на ее фронт, в том числе и идеально захваченные ионы в рампе, в итоге пересекают рамп и становятся пролетными. Как мы видим, в косой МЗУВ, в отличие от строго перпендикулярной, поведение захваченных в рампе ионов существенно зависит от угла θ, критическое значение которого θ* разделяет их на пролетные (θ>θ*) и отраженные (θ<θ*). Кроме того, для косой МЗУВ захваченные ионы в процессе движения в рампе получают значительный прирост энергии так же, как и в случае строго перпендикулярной МЗУВ. Действительно, при углах, близких к критическому, учитывая соотношения (4), (5), мы видим, что пролетные ионы для косой МЗУВ за рампом имеют кинетическую энергию εt ≈tg2θ*, а отраженные Рис. 3. Полученные из численных расчетов траектории ионов для различных значений начальных скоростей s0, значения которых указаны около кривых. D=10, θ=82° попадают в подножье с энергией εa≈2tg2θ*. Подставляя при D>>1 в выражения для энергии значение критического угла cosθ*≈1/D, получим εt≈D2, εa≈2D2. Заметим, что для критических углов, близких к π/2, что характерно для D>>1, в косой МЗУВ энергия пролетных ионов в два раза, а отраженных — в четыре раза больше предельной энергии εm≈D2/2, с которой захваченные ионы покидают рамп и становятся пролетными в случае строго перпендикулярной МЗУВ. Аналогичный эффект существования максимума энергии для отраженных ионов в косых МЗУВ при значении угла, равном критическому, отмечен в работе [Кичигин, 2009б]. Как мы выяснили, в строго перпендикулярной МЗУВ вращающиеся перед рампом частицы отсутствуют, когда значение параметра D<2. В косой МЗУВ, как показывают расчеты, ситуация с вращающимися ионами аналогична, т. е. при D<2 они отсутствуют. Однако отраженные частицы есть при всех D>0 и исчезают только при D→0. Чтобы показать это, обратимся к уравнениям (1)–(3), которые при Ω2<<1 имеют приближенное аналитическое решение. Это второй случай, о котором мы упоминали выше и для которого можно найти аналитическое решение. Как установлено выше, система уравнений (1)–(3) сводится к одному уравнению типа (4) для переменных χ или v. Решаем их методом последовательных приближений, полагая χ=χ1+χ2, v=v1+v2 и выбирая начальные условия в виде s=s0, χ=v0=w0=0. В нулевом приближении, полагая Ω=0, получаем решения для переменных χ1 и v1, выражаемые формулами (5), (7). Далее ищем интересующее нас решение только для переменной χ. Подставляя в (4) χ=χ1+χ2, где χ1=s0τ+(1–s0)sin2θ(τ–sinτ), получим уравнение для χ2: d4χ2/dτ4+(1+Ω2)d2χ2 /dτ2+Ω2cos2θχ2=–Ω2(Bτ+Asinτ), где А=(1–s0)sin2θ, В=А+s0. При Ω2<<1 с точностью до членов, пропорциональных Ω2, получим решение, следующее из этого уравнения: χ2=(В/Ω2)sin Ω2τ–Вτ, где Ω2=Ωcosθ. Таким образом, приближенное решение уравнения (4) имеет вид χ≈(В/Ω2)sinΩ2τ. Как следует из этой формулы, если в момент времени τ=π/(2Ω2), при котором координата максимальна (χ=χm), ее величина χm≥χd= 1/D, то частица становится пролетной. Если же χm<χd, частица возвращается из рампа в подножье и удаляется от рампа в виде продольного пучка. Следовательно, в случае косой МЗУВ, движущейся в холодной плазме, при Ω2<<1 из условия χm=χd=1/D получим зависимость предельного угла θ* от параметров D и s0: [(1–s0)sin2θ*+s0]/(cosθ*)+D(1–s0)sin2θ*=1. (13) Таким образом, для косой МЗУВ критический угол, разделяющий частицы на пролетные и отраженные, зависит как от скорости налетающих на рамп частиц s0, так и от размера рампа, который контролируется параметром D. На рис. 4 приведены для нескольких значений параметра D=0, 0.1, 0.6, 0.8, 1, 2, 3, 10, 50 зависимости предельных углов θ* от величины компоненты скорости s0. Показанная на рис. 4 кривая для D=0 — это зависимость θ0*=θ0*(s0)= =arccos{[(5–4s0)1/2–1]/[2(1–s0)]}, которая получена с помощью формулы (13). Кривая 1 — это теоретическая зависимость (12) θ*(s0) при D=10. Как видно, теоретическая кривая 1 совпадает с расчетной кривой для θ* при малых скоростях s0<0.2, т. е. фактически для захваченных частиц. Необходимо отметить, что зависимости, приведенные на рис. 4, дают возможность оценить как число отраженных ионов, так и долю пролетных ионов, если заданы параметры θ, D и известна температура ионов набегающего на рамп МЗУВ потока плазмы. Отметим некоторые интересные выводы из анализа рис. 4. Значения критического угла θ* в зависимости от параметра D для ионов основной группы (s0≈1) находятся в интервале 0°–60°, а группы захваченных ионов (s0≈0) — в интервале 45°–90°. Для захваченных ионов (s0≈0) угол θ* имеет минимальное значение θ*≈45° при D≈0.6, причем, если D≈0.6 и θ*>45°, все налетающие на рамп МЗУВ ионы в итоге становятся пролетными. Для значений параметра D>2 у всех МЗУВ критический угол θ* для набегающих на рамп ионов, имеющих скорости в интервале 0.7<s0<1, куда входят ионы основной группы, не зависит от D и примерно равен 52°. Далее при D>3 для всех МЗУВ, имеющих углы θ<52°, все набегающие на рамп ионы в итоге становятся отраженными. Очевидно, что главную роль в формировании структуры ударного фронта МЗУВ играют набегающие на рамп ионы основной группы, значения скоростей которых близки к s0≈1. Как показывают наши расчеты, значения критического угла θ*, разделяющего набегающие на рамп ионы на пролетные и отраженные, существенным образом зависят от параметра D. Поэтому важно знать зависимость критического угла от параметра D для ионов основной группы. На рис. 5 показана интересующая нас зависимость θ*(D) для трех значений начальной скорости ионов: s0=0.9, 0.95, 0.99. Как следует из рис. 5, критический угол для ионов основной группы резко уменьшается при изменении параметра D в интервале Рис. 4. Зависимость критического угла θ* от начальной скорости ионов s0 при значениях параметра D=0, 0.1, 0.6, 0.8, 1, 2, 3, 10, 50 Рис. 5. Зависимость критического угла θ* от параметра D для трех значений начальной скорости ионов s0=0.9, 0.95, 0.99 2>D>0.2, а при D<0.2 величина угла θ* практически не зависит от D. ВЫВОДЫ Из используемой в данной работе модели ударного разрыва МЗУВ, учитывающей перепад потенциала в рампе, следует, что все ионы, набегающие на рамп косых МЗУВ, условно можно разделить на следующие категории: 1) пролетные — это ионы, которые с ходу пересекают рамп и больше никогда в него не возвращаются; 2) отраженные — это ионы, которые после простых или сложных движений в рампе выходят из него и удаляются от рампа вверх по течению; 3) вращающиеся — это ионы, формирующие перед рампом подножье; 4) захваченные частицы — это ионы, которые в пределах рампа медленно перемещаются относительно него, поэтому длительное время находятся в рампе. Как вращающиеся, так и захваченные ионы присутствуют во фронте МЗУВ временно. В итоге и те и другие оказываются в строго поперечных МЗУВ только пролетными, а в косых МЗУВ — либо пролетными, либо отраженными. В строго поперечных МЗУВ малая доля захваченных ионов, которые в итоге покидают рамп и становятся пролетными, ускоряется в рампе до энергий порядка D2mu2/2, а захваченные частицы в косых МЗУВ — до энергий, в два раза больших, т. е. до значений порядка D2mu2. Показано, что в косых МЗУВ небольшая часть ионов, вследствие малой начальной скорости в процессе разворота в рампе оказываются временно захваченными. Эти ионы за счет серфотронного ускорения в рампе приобретают энергию до 2D2mu2. С такой энергией ионы выходят из рампа и движутся далее вверх по течению, образуя популяцию отраженных частиц. Таким образом, установлена физическая причина образования отраженных ионов, имеющих значительную энергию, и выявлен механизм их ускорения в рампе. Как следует из работы [Кичигин, 2009б], в околоземной ударной волне предельная энергия 2D2mu2 этих энергичных ионов может достигать значений порядка 1 МэВ. Эти отраженные ионы формируют границу ионного форшока, движутся вдоль этой границы и именно они представляют популяцию продольных пучков (FAB). Найден критический угол θ*, который разделяет плоскость θs0, на которой возможно существование косых МЗУВ, на две области (рис. 4). В одной области (с углами 90°≥θ>θ*) все набегающие на рамп МЗУВ ионы становятся пролетными, а во второй (с углами 0<θ<θ*) — отраженными. Величина критического угла θ*, разделяющего набегающие на рамп ионы на пролетные и отраженные, зависит как от скорости налетающих на рамп частиц s0, так и от пространственного размера рампа, который контролируется параметром D. При больших значениях параметра D (D>>1, размер рампа d< Установлено, что подножье у всех МЗУВ присутствует, если D>2, и отсутствует при D<2. Наличие или отсутствие подножья не зависит от угла θ*. Автор выражает благодарность Еселевичу В.Г. за проявленный интерес к работе и полезные обсуждения. Работа выполнялась при поддержке программы фундаментальных исследований Президиума РАН № 23 «Физика высоких энергий и нейтринная астрофизика» в рамках проекта «Космические лучи в гелиосферных процессах по наземным и стратосферным наблюдениям».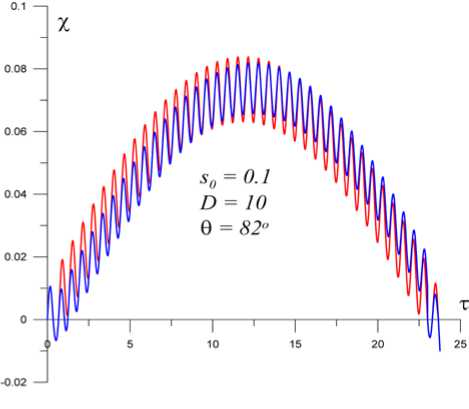
Список литературы Динамика ионов во фронте магнитозвуковых ударных волн
- Ерохин Н.С., Моисеев С.С., Сагдеев Р.З. Релятивистский серфинг в неоднородной плазме и генерация космических лучей//Письма в Астрон. журн. 1989. Т. 15. С. 3-10.
- Кичигин Г.Н. Исследование процесса ускорения ионов во фронте магнитозвуковой ударной волны с изомагнитным скачком//ЖЭТФ. 1992. Т. 101. С. 1487-1509.
- Кичигин Г.Н. Особенности ускорения электронов в серфотроне//ЖЭТФ. 1995. Т. 108. С. 1342-1354.
- Кичигин Г.Н. Серфотронный механизм ускорения космических лучей в галактической плазме//ЖЭТФ. 2001. Т. 119. С. 1038.
- Кичигин Г.Н. Серфинг и генерация космических лучей в релятивистских ударных волнах//ЖЭТФ. 2009a. Т. 136. С. 476-482.
- Кичигин Г.Н. О происхождении энергичных частиц в области форшока околоземной ударной волны//Письма в АЖ. 2009б. Т. 35, № 4. С. 295-303.
- Сагдеев Р.З. Коллективные процессы и ударные волны в разреженной плазме//Вопросы теории плазмы. 1964. Вып. 4. М: Атомиздат, 1964. С. 20-80.
- Alekseyev I.I., Kropotkin A.P. Passage of energetic particles through a magnetohydrodynamic discontinuity surface//Geomagnetism and Aeronomy. 1970. V. 10. P. 755.
- Bale S.D., Mozer F.S. Measurement of large parallel and perpendicular electric fields on electron spatial scales in the terrestrial bow shock//Phys. Rev. Lett. 2007. V. 98, iss. 20, id. 205001
- DOI: 10.1103/PhysRevLett.98.205001
- Bale S.D., Balikhin M.A., Horbury T.S., et. al. Quasi-perpendicular shock structure and processes//Space Sci. Rev. 2005. V. 118. P. 161-203
- DOI: 10.1007/s11214-005-3827-0
- Balikhin M., Gedalin M., Krasnosselskikh V. The scales in quasiperpendicular shocks//Adv. Space Res. 1995. V. 15. P. 247-260.
- Balogh A., Treumann R.A. Physics of Collisionless Shocks. New York: Springer Science Business Media, 2013. 512 p
- DOI: 10.1007/978-1-4614-6099-2
- Chiueh T. Multiple-encounter shock-drift acceleration in nearly perpendicular shocks//Astrophys. J. Pt. 1. 1988. V. 333. P. 366-385.
- Dawson J.M., Katsouleas T. Unlimited electron acceleration in laser-driven plasma waves//Phys. Rev. Lett. 1983. V. 51. P. 392-396.
- Decker R.B. Computer modeling of test particle acceleration at oblique shocks//Space Sci. Rev. 1988. V. 48. P. 195-262.
- Gosling J.T., Thomsen M.F., Bame S.J., et al. Evidence for specularly reflected ions upstream from the quasi-parallel bow shock//Geophys. Res. Lett. 1982. V. 9. P. 1333-1336
- DOI: 10.1029/GL009i012p01333
- Heppner J.P., Maynard N.C., Aggson T.L. Early results from ISEE-1 electric field measurements//Space Sci. Rev. 1978. V. 22. P. 777-789.
- Lee M.A., Shapiro V.D., Sagdeev R.Z. Pickup ion energization by shock surfing//J. Geophys. Res. 1996. V. 101A. P. 4777-4789.
- Lever E.L., Quest K.B., Shapiro V.D. Shock surfing vs. shock drift acceleration // Geophys. Res. Lett. 2001. V. 28. P. 1367-1370.
- Leroy M.M. Structure of perpendicular shocks in collisionless plasma//Phys. Fluids. 1982. V. 26. P. 2742-2753.
- Leroy M.M., Winske D., Goodrich C.C., et al. The structure of perpendicular bow shocks//J. Geophys. Res. 1983. V. 87. P. 5081-5094.
- Newbury J.A., Russell C.T., Gedalin M. The ramp widths of high-Mach-number, quasi-perpendicular collisionless shocks//J. Geophys. Res. 1998. V. 103, iss. A12. P. 29581-29594.
- Ohsawa Y. Conditions for ion reflection in a large amplitude magnetosonic wave//J. Phys. Soc. Japan. 1990. V. 59. P. 2782-2789.
- Schwartz S., Thomsen M.F., Gosling J.T. Ions upstream of the Earth's bow shock: a theoretical comparison of alternative source populations//J. Geophys. Res. 1983. V. 88, N A3. P. 2039-2047.
- Sckopke N., Paschmann G., Bame S.J., et al. Evolution of ion distributions across the nearly perpendicular bow shock: specularly and non-specularly reflected ions//J. Geophys. Res. 1983. V. 88. P. 6121-6136
- DOI: 10.1029/JA088iA08p06121
- Shapiro V.D., User D. Shock surfing acceleration//Planet. Space Sci. 2003. V. 51. V. 665-680.
- Sugihara R.S., Takeuchi N., Sakai K., Matsumoto M. de Acceleration of charged particles by an electrostatic wave propagation obliquely to a magnetic field//Phys. Rev. Lett. 1984. V. 52. P. 1500-1503
- DOI: 10.1103/PhysRevLett.52.1500
- Toptygin I.N. Acceleration of particles by shocks in a cosmic plasma//Space Sci. Rev. 1980. V. 26. P. 157-213.
- Webb G.M., Axford W.I., Terasawa T. On the drift mechanism for energetic charged particles at shocks//Astrophys. J. 1983. V. 270. P. 537-553.
- Wilson III L.B. Low frequency waves at and upstream of collisionless shocks // Low frequency waves in space plasmas. (GMS-216)-AGU-2016. P. 269-292.
- Woods L.C. On double structured, perpendicular, magneto-plasma shock waves//Plasma Phys. 1971. V. 13. P. 289-302
- DOI: 10.1088/0032-1028/13/4/302


