Динамика изменения национального дохода в модели гармонического осциллятора с возмущением

Начиная с середины 1990-х годов в научной литературе опубликовались работы, посвященные эконофизике. Работы [1-3]

посвящены обзору известных в научной литературе попыток провести исследования экономических процессов с использованием теории и методов, разработанных физиками

при решении различных физических задач. В работах [4-6] экономические задачи, связанные с колебанием цен и обьема выпуска товаров, с анализом финансовых временных рядов, с объяснением закона спроса и предложения, решаются в рамках физических моделей с использованием математических методов. Автор монографии [7] предлагает теоретико-методологические основы и математический инструментарий эконофизики. В работе определены понятия экономической скорости, экономического ускорения, экономической силы, экономической работы и экономической энергии. Статьи [8-9] посвящены исследованию временной зависимости национального дохода, который удовлетворяет дифференциальному уравнению гармонического осциллятора. В частности, в [9] исследован случай периодической зависимости от времени внешнего воздействия (внешние инвестиции) без учета и с учетом затухания (трансакционные издержки). В настоящей работе решается аналогичная задача, когда внешнее воздействие зависит от времени в виде произведения экспоненты и периодической функции.

Целью исследования является нахождение и анализ национального дохода как функция от времени, удовлетворяющая неоднородному дифференциальному уравнению гармонического осциллятора с внешним возмущением (внешние инвестиции), когда возмущение имеет вид произведения двух функций от времени: экспоненты и периодической функции.

Постановка задачи и её решение

Так как равновесие в макроэкономической системе считается её динамическое состояние в виде колебательного движе-

ния с малой амплитудой, то представляет определенный интерес рассматривать динамику изменения национального дохода в модели гармонического осциллятора с возмущением.

Рассмотрим модель осциллятора с внешним возмущением и допустим, что национальный доход как функция от времени ( Y ( t )) в этой модели без учета затухания (трансакционные издержки) (коэффициент затухания η = 0) удовлетворяет следующему неоднородному обыкновенному дифференциальному уравнению с постоянными коэффициентами второго порядка

d2Y (t)

—2 ' + ro 0 • Y ( t ) = F_o • e k • cos ro t, (1)

где d ² Y ( t ) / dt ² соответствует темпу изменения национального дохода, ro 0 • Y ( t ) ответственен рыночной силе, которая старается возвращать систему к точке равновесия, ω ₀ – собственная частота колебаний осциллятора, правая часть уравнения показывает внешние инвестиции, меняющихся во времени, k – темп прироста внешних инвестиций, ω – частота колебаний внешних инвестиций, F ₀ – амплитуда колебаний внешних инвестиций.

Отметим, что если для нахождения общего решения однородного уравнения, соответствующего (1), пользоваться методом Эйлера, а для нахождения одного частного решения неоднородного уравнения (1) пользоваться методом вариации произвольных постоянных, то есть искать в виде

У чн (t ) = c 1 ( t ) cos ro ₀t + c₂ ( t ) sin ro ₀t, (2) то относительно неизвестных c ₁( t ) и c ₂( t ) получим следующую систему уравнений:

de,(t)             dc2 (t)

---— • cos ro t +--~ • sin ro t = 0, dt ⁰dt ⁰

de, (t)                  de2 (t)                        kt dt 0    0 dt 0     00

Решение (3) приводит к следующим аналитическим выражениям для c ₁( t ) и c ₂( t )

F kt ci(t ) = 2TO0 •e '

.

Подставляя (4) и (5) в (2) и учитывая, что У ч н ( t ) = c 1 cos to ₀t + c₂ sin to ₀t, где c 1 и c ₂ - положительные постоянные, после некоторых алгебраических преобразований, получим

Y ( t ) = c1- cos to _gt + c₂ sin to _gt + -^ 0- • e^kt • ^{2 to} g

Величины c ₁ и c ₂ в (6) можно определить из следующих начальных условий Коши

Y ( t )| = 0, dYM.

^{( 71} ‘ =°           dt

Вычисления приводят к выражениям

= 0.

t = g

---------• ------------------------------;---;------:---------------г

^{2 to} g    k + ( to - to g )     ^{k +} ( ^{to + to} g )

² 2 to² ₀

-

В частном случае, когда k = 0 из (6) с учетом (8) и (9) получим

Y (t ) =

-

• sin -------— • sin -------—

I

Заметим, что последнее совпадает с результатом, полученным в работе [9]. Стоит отметить, что определенный интерес представляет случай резонанса. Выражение для Y ( t ) в этом случае можно найти, если в (8) перейти к пределу при ω → ω ₀ с учетом (8) и (9). Итак, имеем

Y ( t ) = , F^g , рез       k² + 4 to² _g

2 to² 2 - k ²   .                    e^k ‘ z,                      „ a

—^g-- sin to ₀t - cos to ₀t +-- ( k cos to o t + 2 to ₀ sin to ₀t ) .

k to _g                         k

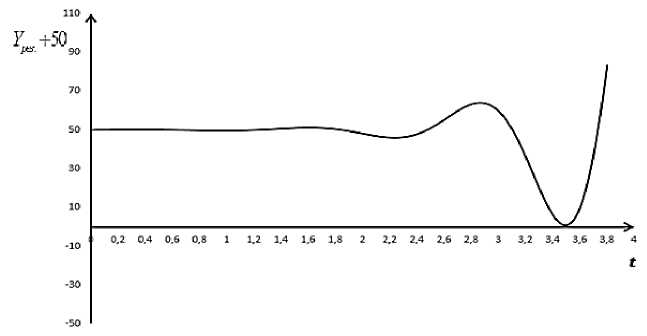
Рис. 1. Кривая изменения Yрез(t) + 50 согласно (11) при η = 0; ω0 = 5; k = 2; F0 = 1; 0 ≤ t ≤ 3,8

Ниже рассмотрим случай, когда η ≠ 0 (учитываем трансакционные издержки). В этом

dY (t)

случае в левой части уравнения (1) добавится член 2n —, то есть функция Y(t) будет dt удовлетворять следующему дифференциальному уравнению

d2Y(t)      dY (t)     7 x kt

----+ 2 n      + ®n • Y ( t ) = F_o • e^k • cos a t.                     (12)

dt2    dt 00

Решая однородное уравнение

d²Y ( t ) dt²

dYt

+ On--^

dt

⁺ ® 0

• Y ( t ) = 0 , получим:

• 1.    ^Yo.o. ( t ) = ( c l ^{+ C}2 • e ) • e "^ при n ² = ® 0 .

• 2.    Y oo. ( t ) = ( c l • e'' • t ^{+ c}2 • e"' ^ ^• t ) • e ’ при n² >  ® 0 .

• 3.    Y o. ( t ) =

c 1 • cos

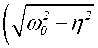
+ c₂ • sin

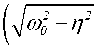
• e ^{n t} при n ² <  ® 0 .

Частное решение уравнения (12) будем искать методом подбора, рассматривая следующие случаи:

• а)    k + i ® не совпадает с - n + i^ ® 0 - n ² при ® 0 >  n ² ( k * - n , ® * V ® 2 - n ²

В этом случае Y _ч.н. ( t ) ищем в виде

Y _ч.н. ( t ) = ( Acosωt + Bsinωt ) · e^kt.                              (16)

где А и B пока неизвестные коэффициенты. Требуя, чтобы (16) удовлетворяло уравнению (12), для коэффициентов A и B получим

^k ( к + ² n ) • F         в =       2F o • ® - ( k + n )

k² ( k + 2 n ) ² + 4 ® ( k + n ) ²        k² ( k + 2 n ) ² + 4 ® ² ( k + n ) ²

Итак, в этом случае общее решение уравнения (12) принимает вид

+ e^kt

Y (t )=

c 1 • cos

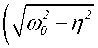
+ c₂ • sin

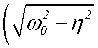
-nt ,

• e ' +

F 0

•----------------------:----------------------------г k2 (k + 2n) + 4®2 (k + n)

•[ k ( k + 2 n ) cos ® t + 2 ® ( k + n ) sin ® t ] .

• б)    k + i ® = - n + i V ® 0 - n ² ( k = - n , ® ² = ® 0 - n ² = ® o - k² ) •

В этом случае Y _ч.н. ( t ) будем искать в виде

• Y _ч.н. ( t ) = t · e^kt · ( Acosωt + Bsinωt ) ,                              (19)

где A и B пока неизвестные коэффициенты. Требуя, чтобы (19) удовлетворяло уравнению (12), для A и B получим

A = 0, B = F ₀ / 2 ω ,

ТогДа Y ₄ . _H . ⁽ t ) = F^L t • e kt • sin ® t и общее решение уравнения (12) принимает вид 2 ®

• Y ( t ) = e^kt • c 1 cos ® t + 1 c₂ +—-• t I- sin ® t .

I      2 ® J

Постоянные c ₁ и c ₂, которые входят в (18) и (21), находятся с помощью начальных условий Коши (7) и выражаются формулами:

а)

k ( k + 2 n ) • F_o k² ( k + 2 n ) ² + 4 ® ² ( k + n ) ²

^С2 =

( k + n ) [ 2 ® 2 - k ( k + 2 n ) ]" F 0 to to- 2 • [ k² ( k + 2 n 2 ) + 4 o' ( k + n ) 2 ]

б) c ₁ = c ₂ = 0. (24)

Ниже приведем общее решение дифференциального уравнения (12) в случаях а) и б).

а)

Y (t )=

F 0

k² ( k + 2 ц ) ² + 4 о? ( k + n ) 2

i e

.- n t

( k + n ) ( 2 to 2 — k² — 2k n ) 7 ® c —ⁿ

• Sin

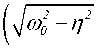
• t ) - k ( k + 2 n ) cos ( ^® 0 — n 2

• t1

+

б)

Если в (25) и (26) перейти к пределу при ω → ω ₀ (случай резонанса), то получим выражения для Y _рез ( t ) в случаях а) и б) в виде:

а)

F 0

- n 2 ♦ t ) - k ( k + 2 n ) cos (7^

<

® o ^-

ⁿ ♦ ^t ) ]⁺

♦

- n ²

+ [ k ( k + 2 n ) cos to ₀t + 2 ro ₀ ( k + n ) sin ® o t ] ♦ e kt } .

б)

Y ( t ) = -^ 0- • t • e k • sin ro t. . рез        2 to₀               ⁰

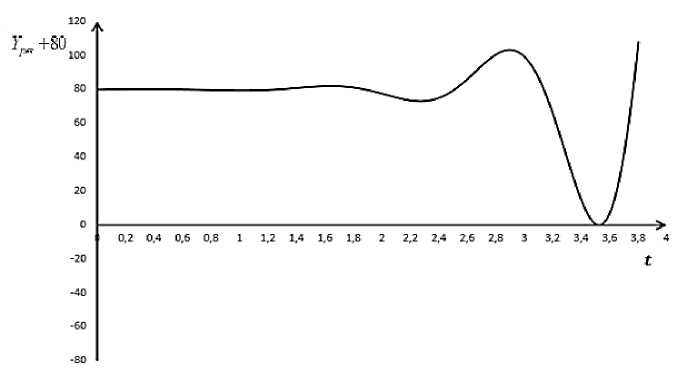
Рис. 2. Кривая изменения Y_рез(t) + 80 согласно (27) при k + i to *-n + i to 2 - n²; П = 0,1; ro₀ = 5,6; F₀ = 1; 0 < t < 3,8

Из графиков изменения Y ( t ) в случае резонанса (рис. 1-3) виден колебательный характер динамики национального дохода в зависимости от времени. Во всех трех случаях минимумы и максимумы достигаются почти при одном и том же значении t , но они отличаются своими величинами.

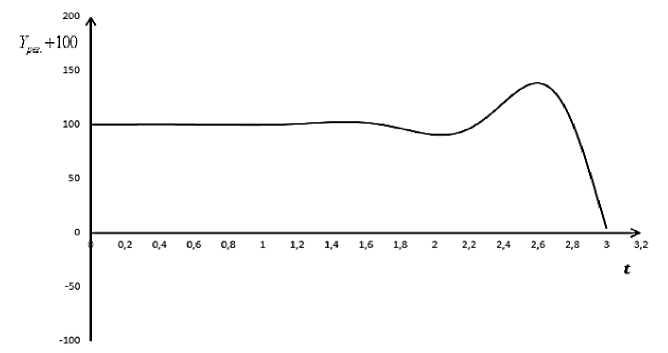
Рис. 3. Кривая изменения Y_рез(t) + 100 согласно (28) при k + i ro = -n + i 7 ® 0 - П 2 ; k = 2; П = 0,1; ® o = 5,6; F₀ = 1; 0 -1 - 3,8

Заключение

В работе в физической модели осциллятора с внешним возмущением (внешние инвестиции) исследована динамика изменения во времени национального дохода. Предполагается, что внешние инвестиции зависят от времени в виде произведения показательной функции (экспоненты) и периодической функции. Рассмотрены случаи, когда пренебрегаем трансакционными издержками и когда их учитываем. Проведен-

ный аналитический и графический анализ результатов в случае резонанса показывает, что колебательный характер Y ( t ) сохраняется. Отметим также, что проведенное в данной работе исследование представляет интерес и с точки зрения развития теоретической эконофизики, и с практической точки зрения возможности использования материалов исследования при чтении курса «Моделирование макроэкономики» для студентов высших учебных заведений.