Динамика кавитационных пузырьков в расплавах легкоплавких металлов в ультразвуковом поле
Автор: Асташкин Ю.С.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Математика, информатика и инженерия
Статья в выпуске: 7 (49), 2019 года.
Бесплатный доступ
Пульсации пузырьков с воздухом и аргоном с начальным радиусом 1-10 микрон при амплитудах переменного давления 1-12 атмосфер исследовались на основе численных решений уравнений Рэлея - Плессета, Флинна и Кирквуда - Бете -Джилмора. Представлены результаты расчетов пульсаций пузырьков, порогов кавитации, критерия коллапса пузырька для расплавов легкоплавких металлов и воды.
Ультразвук, кавитационные пузырьки, расплавы легкоплавких металлов
Короткий адрес: https://sciup.org/140274851
IDR: 140274851 | УДК: 534-8
Текст научной статьи Динамика кавитационных пузырьков в расплавах легкоплавких металлов в ультразвуковом поле
Результаты исследований воздействия ультразвука в диапазоне f =20-50 кГц на процессы дегазации, кристаллизации металлов и сплавов, металлизации поверхности, пайки и диффузии в расплавах металлов приведены в ряде работ [1-9]. В этой связи изучение пульсаций кавитационных пузырьков и определение пороговых давлений, при которых в расплавах металлов происходят нелинейные явления, используемые в технологиях, представляет практический интерес [3,4-7]. При исследованиях пульсаций кавитационных пузырьков в расплавах металлов, проведенных ранее, полагалось, что постановка задачи, принятая в [10] для жидкостей справедлива для расплавов металлов, в случае преобладания инерционного эффекта, [3]. Уравнения динамики парогазовых пузырьков с учетом свойств и сжимаемости расплавов металлов решались в [9,11]. Объем молекул газа в пузырьке (согласно уравнению Ван де Ваальса), что важно при расчете коллапса пузырька, был учтен в более поздних работах, обзор которых приведен в [12,15]. Давление паров в расплавах ряда легкоплавких металлов в интервале температур ~(1,1-1,3)*Тпл: pv « 1тора (таблица1), поэтому в этом интервале температур можно принять Pv « Рд и рассматривать пузырек как газовый,
Рост газового пузырька в жидкости, насыщенной газом при статическом давлении Р0 в ультразвуковом поле, определяется медленным (относительно периода колебаний) процессом выпрямленной диффузии [13]. Численные расчеты величины (R(t)/R0) пузырьков с начальным радиусом R0 = 1 ^ 10 микрон в расплаве алюминия, проведенные с учетом и без учета выпрямленной диффузии водорода, практически не отличаются [4]. Заметный рост диффузии газа происходит при амплитуде переменного давления выше порога кавитации, а его максимальное значение достигается в режиме развитой кавитации [4]. Аналитические приближения, позво- ляющие производить оценки динамики газовых пузырьков при учете воздействия ряда физических факторов, в том числе тепломассопереноса и устойчивости сферической формы пузырька были представлены Плессе-том и Хси (Din-Yu Hsieh) в известных обзорах [13]. Стабильность сферической формы пузырька без учета вязкости и сжимаемости определяется 1 24<7 3
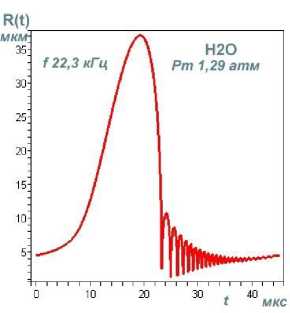
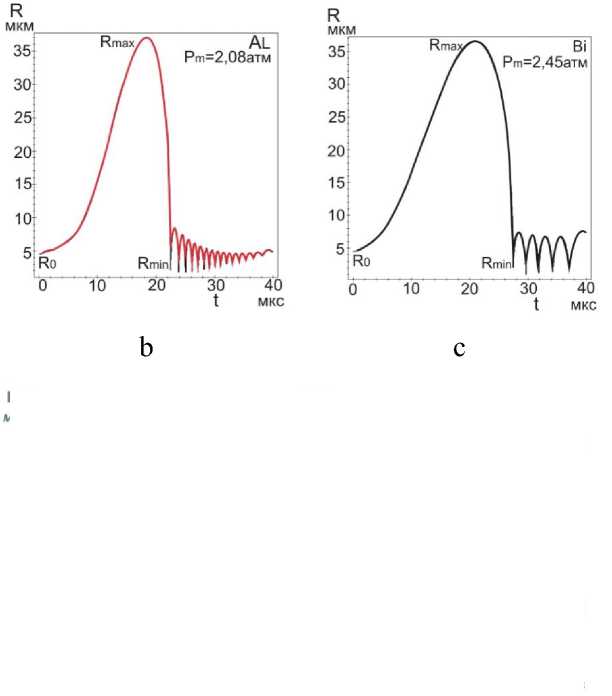
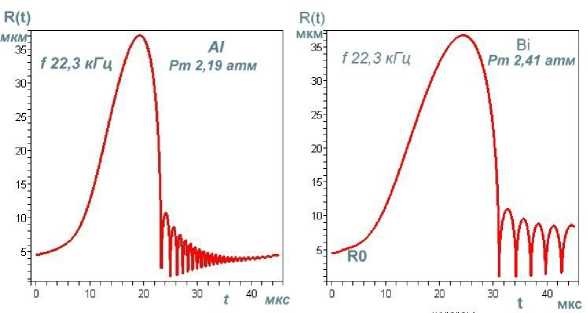
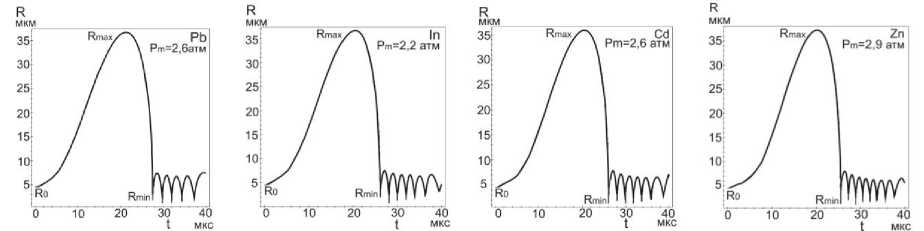
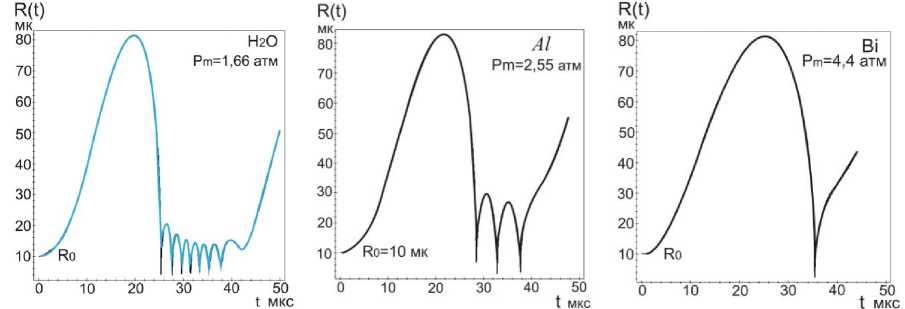
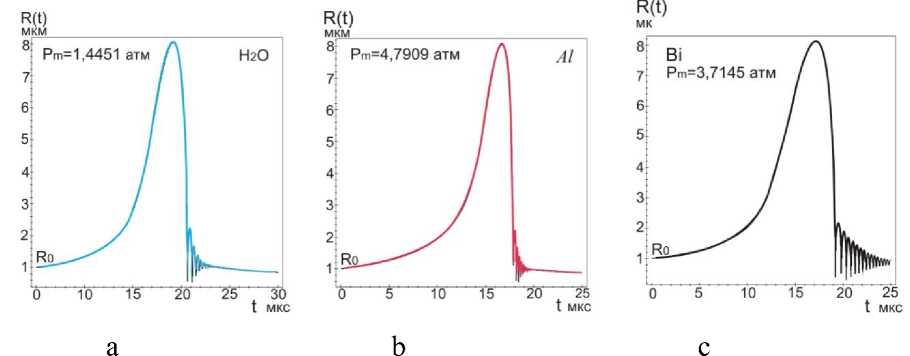
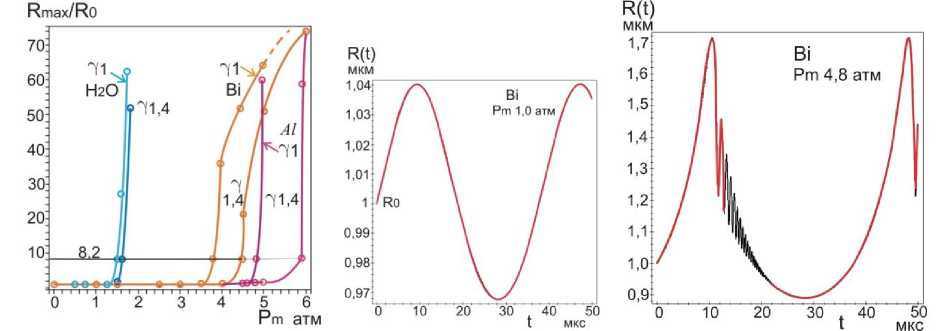
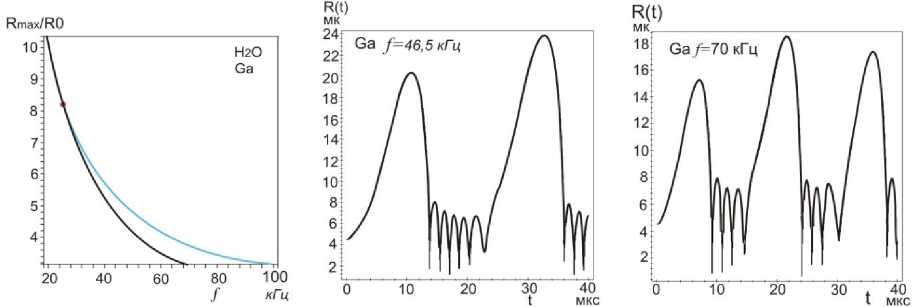
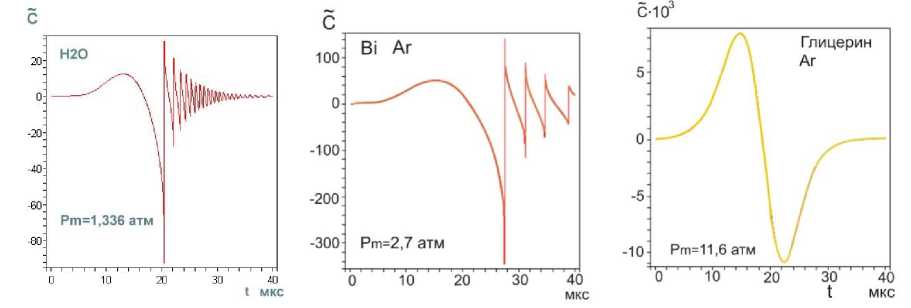
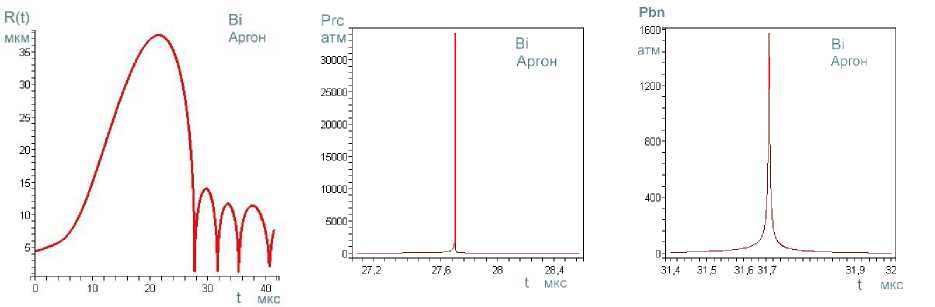
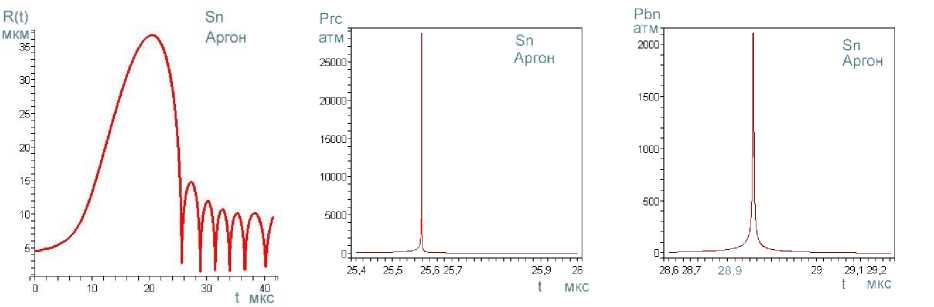
выражением: Rst ~ (;г^“7) , где о — поверхностное натяжение, р - плот- ность, ω=2πf. Это выражение получено при линеаризации уравнения Рэлея по 5: R = R0 [1 + 5sin( микрон, и сферическая форма пузырьков с радиусом Ro = 1 ^ 10 микрон в таком приближении может рассматриваться, как стабильная. Численные расчеты, по методу Плессета с учетом поверхностного натяжения, вязкости и сжимаемости при линеаризации уравнения Херинга – Флинна [10] были выполнены в работе [14]. Результаты расчетов для воды показали, разную степень влияния этих свойств воды на стабильность радиальных пульсаций и устойчивость сферической формы в зависимости от соотношения возбуждающей - ю и резонансной - ш0 частот. Вязкость снижает амплитуду низших гармоник, а поверхностное натяжение делает более устойчивым сферическую форму за счет влияния на высшие гармоники. В расплавах металлов сферическая форма пузырька более устойчива: вязкость и поверхностное натяжение больше, чем в воде. У расплавов алюминия и цинка – μ почти в три раза превышают вязкость воды, у галлия и цинка - о больше на порядок (табл.1). При величине ю « ш0, росте возбуждающего давления и захлопывании пузырька влияние свойств ослабевает, а при коллапсе пузырька свойства жидкости не оказывают заметного влияния на устойчивость сферической формы пузырька [14]. Исследования в области сонолюминесценции одиночного пузырька (SBSL) установили границы параметрической нестабильности пузырька, определяемой амплитудой давления и начальным радиусом R0. Эта нестабильность снижается при увеличении вязкости. Нестабильность Релея – Тэйлора с характерным временем 10-9 секунды, определяемая высокоскоростным потоком газа из пузырька в процессе его коллапса, снижается при уменьшении начального радиуса Ro [12,15]. Процесс пульсаций может быть изотермическим или адиабатическим в за- висимости coотношения скорости теплопереноса и скорости движения стенки пузырька R в соответствии с числом Пекле: RR , где ^ - термодиф- фузионная длина. Если радиус пузырька R > <^, то процесс можно считать адиабатическим [13а]. Теплопроводность расплавов легкоплавких металлов (самая низкая у висмута - 14,6, самая высокая у алюминия -101 Вт./м^С) значительно превышает теплопроводность воды - 0,56 Вт./м-°С [17-22]. Теплопроводность T—T в значительной степени определяет соотношение температур: е =----, где T Ts- температура на поверхности пузырька, Т - температура жидкости, Тд -температура газа в центре пузырька [13,15]. При значении е~10-3 — 10-2 изменение температуры в основном происходит внутри пузырька, и для жидкости можно принять Ts = Т, что также соответствует случаю расплавов металлов. Для случая воды, в слабых и умеренных полях ( Рт< 15 атм ), величина у = Cp/Cv [16]. Значения порогов кавитации для расплавов металлов, рассматриваемых в данной работе, находятся в интервале слабых и умеренных ультразвуковых полей (Р т< 5) атм, и можно принять у = 1,4 при адиабатическом сжатии воздушного пузырька и у = 1, при изотермическом расширении , а для пузырька с аргоном и другими одноатомными газами у = 5/3. Таблица 1. Свойства некоторых легкоплавких металлов [17-22]. Температура плавления Тпл , давление пара (на линии насыщения) Р„ , плотность жидкости Pi, скорость звука в жидкости Ci, поверхностное натяжение с, динамическая вязкость ц . Металл вещество 1 Tпл °C Рр тор (мм.рт.ст.) pi кг/м3 с1 м/сек с • 103 Н/м ц • 103 Па∙сек Al 660 1 (1537С) 2369 4750 520 2,9 Zn 419 1 (487С) 6920 2700 785 3,17 Pb 327 1 (955^) 10510 1760 442 2,12 Bi 271 1 (712Т) 10030 1660 376 1,66 Sn 232 1(1154^) 6830 2450 526 1,67 In 156 1(727^)) 7260 2215 340 2,0 Я2О 0 (лёд) 17,2 20Т 1000 1481 73 1 Cd 321 1 (394Т) 7790 2215 564 2,3 Ga 30 1(950Т) 6095 2740 720 1,82 СзНА 290 (tk) 10-3 20Т 1261 1923 59,4 1495 В предлагаемой работе исследования пульсаций пузырьков проводились на основе численных решений уравнения РП в форме [15]: р1и<к+\кП Р^ !>(,. !>„.("У;Д1^',) 2; ^'R (1) Начальные условия: R (0) = R0 , R(0) = 0, R - радиус пузырька, 2оА RR--h.3\Y давление газа в пузырьке: Рд = (Ро + ~) (д3 ^3 ) (2) ^3= —пЬ , 4тт b – коэффициент, учитывающий объем молекул газа в пу- зырьке в молях (по уравнению Ван дер Ваальса), n – число молей газа, величина h – радиус сферического объема, занимаемого молекулами [16]. Для воздуха ^- = 8,54 , для аргона - 8,82 [12,15]. выражение для внешнего давления (—Р(() — Ро) принято в виде [10]: Р^ = Ро — Pmsin(tot), при t=0, Р„(0) = Ро Сопоставление результатов численных расчетов для воды в интервале времени Л1=4,5 мкс и начальном радиусе R0 = 4,5 микрона c численными и экспериментальными результатами работы [24] и с принятыми значениями свойств в [24] показало хорошую сходимость как для текущего радиуса R(t) , так и его минимального значения Rm/n = 0,45-0,5 микрон (рис. 1а,b). Зависимости R от времени для воды и расплавов на частотах 25,6 и 22,3 кГц приведены на рис. 1. При изменении величины у, частоты f, при условии постоянства отношения Rmax/R0, характер пульсаций пузырька не изменяется. Общей особенностью пульсаций пузырька в воде и расплавах является малые колебания после коллапса, называемые в литературе отскоками (bounces). Возникновение таких колебаний в воде отмечалось в ряде работ и обзоров [10,11,12]. Их количество при изменении частоты f от 22,3 до 26,5 кГц и величины у = 1 ^ 1,4 мало изменяется (рис. 2a,b,c,d,e,f и 3a,b,c). С учетом этого и, рассматривая расплавы и воду как модельные жидкости можно оценить влияние свойств жидкости на коле- бания пузырьков. Частоту малых колебаний можно оценить по формуле Миннерта (3), если принять, что это собственные колебания пузырька [12,24,25], а с учетом вязкости по формуле Триллинга (3а) [14]. a d e f Рис.1 Пульсации воздушного пузырька R0 = 4,5 микрон в воде, в алюминии и в висмуте при соотношении Rmax/R0 = 8,2 ; (a,b,c) f = 26,5 кГц , у = 1; (d,e,f), f =22,3 кГц , у = 1,4. f = — /— (Po + —) (3) '0 2ttR„^ p V 0R„J x ' 1 3! 2Z f0 2. Ro ^p(Po + Ro — _2»_) — (Z^V 3/RoZ RroP) (3a) Минимальная плотность у воды и алюминия. который относится к легким металлам (табл1), но его вязкость более чем в два раза превышает вязкость воды и согласно формуле Триллинга при R0 =4,5 микрон для воды: f0 = 708 кГц, для алюминия f0 = 726 кГц,. Это соответствует длительности их первого колебания после коллапса (рис.1). Уместно отметить, что зависимость длительности этих колебаний от времени имеет нелинейный характер для всех расплавов и воды, и это не позволяет непосредственно связать их длительность с резонансной частотой f0 , во всем рассматриваемом интервале времени (~20-40 мкс), поскольку выражение (3, 3а), получено при линеаризации уравнений колебаний [14,25]. Значения резонансных частот f0 для первых рассматриваемых колебаний пузырька R0 = 4,5 микрон, у = 1,4 в расплавах находятся в пределах 317 ^ 726 кГц, минимальные - у тяжелых металлов (их плотность на порядок выше, чем у воды): у расплава висмута 317 кГц, у свинца 326 и, максимальное – у алюминия. Резонансные частоты f0 пузырьков при значениях R0 = 1 ^ 10 микрон выше частоты возбуждения f=26,5 кГц и частот технологического диапазона 17-50 кГц, а величина радиуса R0 в указанных пределах меньше резонансного радиуса R0< R0T. Это является одним из необходимых условий возникновения кавитации в воде и в расплавах [3,25] . a b c d Рис.2 Пульсации воздушного пузырька в расплавах индия, свинца, кадмия и цинка. R0 = 4,5 микрон у = 1, f=26,5 кГц. Изучение малых колебаний, возникающих после коллапса пузырька, представляет практический интерес, поскольку при пороговых давлениях в расплавах некоторых металлов, как будет показано ниже, такие колебания, могут вызывать повторный коллапс пузырька с излучением волн конечной амплитуды, а в эксперименте вносить существенный вклад в белый спектр кавитационного шума. Расчетные значения порогов кавитации Ртс (атм,1,013 бара) для воды и расплавов приведены в таблице 2 для пузырьков с R0 = 4.5 мкм, (Rmax/R0 = 8,2). Таблица 2. Пороги кавитации в расплавах металлов и воде. f 25,6 кГц H2O Al In Bi Sn Pb Cd Ga Zn СаНвОа Воздух у = 1 1,285 2,10 2,20 2,45 2,45 2,60 2,60 2,70 2,90 11,5 У 1,4 1,325 2,27 2,35 2,63 2,65 2,78 2,85 2,98 3,18 11,6 f 22,3 кГц У 1,4 1,29 2,19 2,17 2,41 2,47 2,55 2,66 2,82 3,02 10,1 Ar у =5/3 f 25,6 кГц 1,336 2,36 2,40 2,70 2,74 2,85 2,94 3,10 3,29 11,6 Pt 0,84 1,91 1,57 1,64 1,92 1,77 1,98 2,23 2,32 0,78 Значение Рт=11,5 атм для глицерина получена при численных расчетах уравнения РП (2) с учетом вязкости р= 1,49 Па^с. Это свидетельствует о преобладании вязких сил при пульсации пузырька в чистом глицерине. В этом случае при давлениях 10,1–11,6 атм кавитация на малых пузырьках в глицерине не возникает, пузырек совершает нелинейные колебания, но в фазе сжатия коллапса не происходит. В насыщенной растворенным газом жидкости при давлении Р0 концентрация газа сю вдали от пузырька равна равновесной концентрации с0. Если жидкость не насыщенна растворенным газом, то концентрация газа вдали от пузырька сю < с0 [13]. Плессет и Хси на основании решения уравнения диффузии с учетом конвективного члена получили аналитические выражения для баланса диффузионных потоков в колеблющийся пузырек и из пузырька в жидкость ^ = ^- , а также аналитическое выражение для максимального переменного давления, при котором этот баланс реализу- ется: Pt = (l)^ Р0 (1 + ^ — г) (4) 2/ ^0—0 Со Значения величины Pt для расплавов металлов воды и глицерина при Ро = 1 атм и отношения сю/с0 = 0,85 приведены в таблице 2. Эта величина может быть принята за нижнее значение порога кавитации в условиях выпрямленной диффузии. На рис. 3 приведены пульсации пузырька R0 = 10 микрон при тех же параметрах, что и на рисунке 1,2. Захлопывание пузырька в расплавах металлов происходит позднее, чем в воде (3^6 мкс до T/8) рис. 1-3. При увеличении радиуса R0 c 4,5 до 10 микрон, частота малых колебаний для случая воды и алюминия уменьшается Рис.3. Пульсации воздушного пузырька R0 = 10 микрон Rmax/R0 = 8,2 f=25,6 кГц . В висмуте при значении R0 = 10 микрон эти колебания отсутствуют, а при значении R0 = 4,5 - возникают с более низкой частотой, чем для алюминия и воды, поскольку плотность висмута на порядок больше, чем у воды и в четыре раза больше, чем у алюминия. Рис.4 Пульсации воздушного пузырька R0 = 1 микрон частоте 26,5 кГц, в воде и в расплавах Al и Bi при отношении Rmax/R0 — 8,2 Характер пульсаций пузырьков при фиксированных значениях свойств жидкости определяется начальным радиусом. Представляет интерес исследование пульсаций пузырька при значении R0 = 1 микрон (рис.5), поскольку такой пузырек можно рассматривать как зародышевый, по крайней мере для расплавов и жидких металлов [26]. Количество малых колебаний после коллапса падает с увеличением R0: при R0 = 1 микрон, наибольшее, при R0 = 10 микрон - наименьшее и в случае висмута они исчезают (рис.1-4). В данной работе для пузырька радиуса R0 = 1 микрон были рассчитаны зависимости Rmax/R0 от амплитуды давления Pm (рис.5). Во всех представленных случаях при давлении меньше критического Pm « Ртс (нижняя горизонтальная линия на рисунке 5а) пузырек совершает малые периодические колебания с частотой возбуждения (рис.5b). Рис. 5. Зависимость отношения тах для воздушного пузырька Ro = 1 микрон в распла-«о вах алюминия, висмута и в воде. С ростом давления Рт< Ртс малые линейные колебания переходят в нелинейные. а нелинейные – в нелинейные колебания сложной структуры (рис.5с). При амплитуде давления Рт = Ртс, (верхняя горизонтальная линия на рисунке.ба) отношение Rmax/Rmin — 8,2 , и колебания со сложной структурой (рис.5с) переходят в колебания, характеризующиеся коллапсом (рис 4a,b,c). Критическое давление Ртс наименьшее для воды, максимальное - для алюминия. Значение величины Rmаx/RmlTг — 8,2 позволяет фиксировать переход от нелинейных колебаний к колебанияv с коллапсом пузырька и началу роста зародышевого пузырька R0 = 1 микрон с большим значением отношения: ^(^max/^o) ^^т ~(20 ^50)104 На основе ряда численных решений уравнения РП (2), проведенных в данной работе для расплавов металлов и воды, были получены зависимости величины Rmax/R0 от частоты f. Кривая этой зависимости, определенной по первому колебанию для расплавов и воды, носит гладкий характер (рис.6а). (Точкой отмечено значение 8,2 при f=26,5 кГц). Величина Rmax/R0 уменьшается с ростом частоты. Частотные зависимости порогов кавитации для случая воды в широком диапазоне частот исследовались в [27]. Изменение характера пульсаций, c увеличением частоты f имеет более сложный характер, что связано с развитием структурной неустойчивости пульсаций пузырька в расплавах некоторых металлов (рис. 8b,c). Структурная устойчивость для случая воды подробно исследовалась в работе [10], а в расплавах рассматривалась для случая пузырьков с начальным радиусом на порядок больше, чем в данном случае [11]. a b c Рис.6аЬс. Пульсации воздушного пузырька R0 = 4,5 мкм в воде и галлии при увеличении частоты f: а) изменение величины Rmax/R0 , определяемого по первому колебанию в диапазоне 20-100 кГц, b) и с) развитие структурной неоднородности пульсаций пузырька в галлии с ростом частоты, (начиная с f = 40 кГц). Для определения порога и степени развития кавитации в расплавах метал лов, чистом глицерине и воде на пузырьках c начальным радиусом R0 = 1 ^ 10 мкм применялся дифференциальный критерий с , предложенный и протестированный в [28]: с =- /dR(t)\ pR(t) dt ) 8р Величина дифференциального критерия с для случая пузырька с воздухом после коллапса и при пульсациях с малым размахом (bounces) вычислялась при численном решении уравнения РП (2). Наименьшие значения критерия получены для случая глицерина (на 5 порядков ниже, чем для расплава висмута и на два порядка ниже, чем для воды). Во всех представленных случаях для расплавов, значение с » 1 , что характерно для развития кавитации и ее нелинейных эффектов. Пороги кавитации приведены в таблице 2. Величина дифференциального критерия с, чисел Маха т1, температуры и давления Рд газа в пузырьке с аргоном рассчитывалась на основе численных решений уравнения Флинна [30]. Уравнение Флинна принято в форме: р lR (1 - 1Л)R+2(1 - ^ *} R2] =(1+^)№) - Р»] + 2И1—^КР(/г) (6) Внешнее давление: Рю = Р0 — Pmsin( Р^") = Рд -2‘ -^К . Начальные условия: R(0) = R0, R(0) = 0. b a c Рис. 7abc. Изменение критерия кавитации c(t) при расширении и сжатии пузырька с аргоном R0 = 4,5 мкм , f=26,5 кГц при соотношении Rmax/R0 = 8,2 , a) H2O, b) Bi, c) глицерин. Изменение критерия c(t) для пузырька с аргоном в воде, расплаве висмута и в глицерине приведены на рис. 7a,b,c. Отрицательные значения с характеризуют процесс сжатия пузырька, положительные – его расширение. Характер зависимости c( t) при расширении пузырька с аргоном в воде и в висмуте по сравнению со случаем пузырька с воздухом не изменяется, но пиковые значения критерия после основного колебания значительно больше (~60%). Значения критерия для первых четырех малых колебаний c(t) >10, что выше порога кавитации). Величина c(t) для пузырька с аргоном в глицерине не изменяется (рис.7c). Пузырек совершает нелинейные колебания, и кавитация отсутствует (рис.7с). Сжимаемость жидкости на основе приближения Кирквуда–Бете учитывается в известном уравнении Кирквуда – Бете – Джилмора [10,29]. В расплавах металлов при малых значениях R0 излучение волн конечной амплитуды может происходить при малых колебаниях пузырька [11]. Для расчета пиковых значений давления вблизи стенки пузырька численно решалось уравнение Кирквуда - Бете - Джилмора (КБД) в форме [10]: RR(’ 1R) I 3(| 1R)R2 (1 I 1R)" + 1R(1 1 R)RdH (7) С 2 3 С их их С c = [c02 + (п — 1)Н]1/2 - локальная скорость звука с0 = (Лн/р0)1/2 - скорость звука в невозмущенной среде ^т) Н - энтальпия с учетом вязкости на границе пузырька п-1 Н > V{h 2;-Т - ВМ -(Р ' BiVJ (8) Л, В,п - постоянные из уравнения состояния для конденсированных ве- ществ [10,31]: Р = Л (-^V Ро — В, для олова: Л = 7 • 104 атм, (= 7 • 105Па) , п = 5,4; для висмута: Л = 3.368 • 104 , (- 3.368 • 104 Па ), п = 8,1. Показатель нелинейности n для расплавов металлов рассчитывался по уравнению состояния, приведенному в работе [32]. В формуле давления газа Рд (6) учитывалась поправка Ван дер Ваальса [12,15]. В таблице 3 и на рисунках 8-9 приведены результаты численных расчетов уравнения Кирквуда – Бете – Джилмора при пороговом давлении Рт = 2,7 атм для расплавов висмута и олова. a b c Рис.8 a) Пульсации пузырька c аргоном R0 = 4,5 микрона в расплаве висмута b) давление в волне, излучаемой после коллапса, c) тоже после первого малого колебания. a b c Рис.9 а) Пульсации пузырька с аргоном R0 = 4,5 микрона в расплаве олова, b) давление в Таблица 3. Пиковые значения давления после коллапса РТС, после первого малого колебания - РЬп, число Маха для жидкости - тг, критерий - с, давление газа - Рд и температура газа - Тд. Экспериментальные исследования, проведенные в работе [34] с применением быстродействующей стрик-камеры с разрешением 0,5 наносекунды и миниатюрного датчика позволили зафиксировать и визуализировать ударную волну давления, излучаемую кавитационным пузырьком после коллапса [33]. Пиковое давление в ударной волне оценивается в ~40-60 килобар (~4 • 104) атм скорость стенки пузырька ~950 м/с. Результаты численных расчетов для воды, полученные в работе [10] РТС~ 50-60 килобар. Расчетные оценки числа Маха - тг данной работы: для расплавов ~ 0,15-0,4, для воды ~0,6, что соответствует для воды значению скорости ~890 м/с.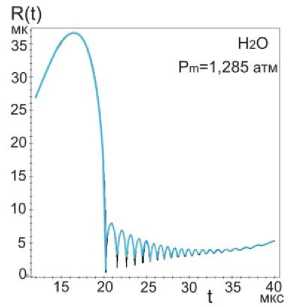
Расплав
РТС атм
РЬп атм
тг
с
Рд атм
Тд°К
висмут
3,4 • 104
1,6 • 103
0,345
440
1,16^105
3,1^ 104
олово
2,9 • 104
2,1 • 103
0,18
330
1,16^105
3,0-104
волне, излучаемой после коллапса c) тоже после первого малого колебания.
Список литературы Динамика кавитационных пузырьков в расплавах легкоплавких металлов в ультразвуковом поле
- Abramov O.V. High-Intencity Ultrasonics. Theory and Application// N.Y. OPA, 1998, Amsterdam. CRC press, 1999. -700 с.
- Eskin G.I., Eskin D.G. Ultrasonic treatment light alloy melts.// Gordon and Breach. Amsterdam. 1998, CRC press, Amsterdam, 2014
- Абрамов О.В. Физические основы процессов кристаллизации металлов в ультразвуковом поле.// Воздействие мощного ультразвука на межфазную поверхность.// Ред. А.И. Манохин. М. Наука. 1986 -275с.
- Эскин Г.И. Ультразвуковая обработка цветных металлов и сплавов.// В кн. Там же.
- Абрамов О.В., Абрамов В.О., Муллакаев М.С., Артемьев В.В., Анализ эффективности передачи ультразвуковых колебаний в нагрузку. //Акуст. журн., т.55, 2009 -820- 844.
- Кундас В.Л., Ланин В.Л., Тявловский М.Д., Достанко А.П. Ультразвуковые процессы в производстве изделий электронной техники, т.1. Минск. Беспринт. 2002 - 404 с.
- Бертник Ю.Н., Тризна Ю.П., Панов Л.И., и др. Исследование кавитации в расплавленном припое. В сб.: Применение новых физических методов интенсификации металлургических процессов. М. Металлургия. 1974 -166-170 с.
- Абрамов О.В., Асташкин Ю.С., Петровский В.А. К оценке давлений, возникающих при развитии кавитации в расплавах легкоплавких металлов.// Там же: 1974 -161-166с.
- Акуличев В.А. Пульсации кавитационных полостей.// Мощные ультразвуковые поля. Ред. Л.Д.Розенберга. М. Наука. 1968 -131-166 с.
- Асташкин Ю.С., Пугачев С.И., Петровский В.А. Ультразвуковая кавитация в жидких легкоплавких металлах и сплавах. //Технология судостроения, 8, 1974 -103-108 с.
- Hingelfeldt S. Brenner M.P. Grossmann S. and Lohse D. Analysis of Rayleigh - Plesset dynamics for Sonoluminescing Bubbles. // J. Fluid Mech. v. 365, 1998 -171-204 p.
- Plesset M.S. Bubble dynamics. // Cavitation in real liquids. Proceed. of the symposium. Elsevier publ. comp. Amsterdam - London - NY. 1964 -1-18 p.
- Гасенко В.Г., Колесников Л.Е., Соболев В.В., Исследование устойчивости сферической кавитационной полости в звуковом поле. ПМТФ, №6, 1973 г., с. 109-114.
- Brenner M.P., Hingelfeldt S and Lohse D. Single-bubbles sonolumenscene //Reviews of modern Physics, v 74, April, -2002, -25-82.
- Маргулис М.А. Сонолюминесценция. // УФН, т.170, 3, 2000 -263с.
- Несмеянов А.Н. Давление пара химических элементов. М. Изд-во. АН СССР, 1961 -387 с.
- Гитис М.Б., Михайлов И.Г. Распространение ультразвука в жидких металлах. // Акуст. журн., т.12, в.2, 1966- 145-149с.
- Чиркин В.С. Теплофизические свойства материалов. //М. Госиздат физмат., лит. 1959 - 353 c.
- Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей.// 1 изд. М. Наука. 1952 -720 с. 423 с., 2 изд. //М. Наука. 1972 -720 с. 423 с.
- Андронов В.Н., Чекин Б.В., Нестеренко С.В. Жидкие металлы и шлаки. //Справ. Изд. М. Металлургия. 1977 -128 с.
- Зиновьев В.Е. Теплофизические свойства металлов при высоких температурах. Справ. изд. // М. Металлургия. 1989 -384 с.
- Gaitan F.D. and Crum L.A. J. Acoust. Soc. Suppl. S141, -1990.
- Barber B.P. Putterman S.J. Light scattering measurement of the repetive supersonic implosion of a sonoluminescing bubble. // Phys. Rev. Letters, v.69, 26, 1992 -3839-3842 p.
- Сиротюк М.Г. Экспериментальные исследования ультразвуковой кавитации. // Физика и техника мощного ультразвука, т. 2, 1968 -169-218.
- Двайвер О. Теплообмен при кипении жидких металлов. //М. Мир. 1980 -516 с.
- Noltingk B.E. Neppiras E.A. Cavitation produced by Ultrasonics. //Proc. Phys.Soc. v.63, 1950 - 674 p.
- Bogoyavlenskiy V.A. Differential criterion of a bubble collapse in viscous liquids.// Physical Review E, 60, 1, 1999 -504-508 p
- Перник А.Д. Проблемы кавитации. //Л. Судостроение.1966 -310 с.
- Flynn H.G. Cavitation dynamic I //J.Acoust. Soc.Am. v.57, 1975 -1379, Cavitation dynamic II //v.58, -1160 p.
- Зельдович Я.Б. Райзер Ю.Н. Физика ударных волн и высоко температурных гидродинамических явлений. М. Наука, 1965
- Вебер Д., Стефенс П. Распространение ультразвука в жидких металлах и сплавах. //т.4, часть Б, М. 1974 -75-122 с.
- Pesha R. and Compf B. Microimplosions: cavitation collapse and shock wave emission on nanosecond time scale.// Phys. Rev. Lett., 84, 2000 - 1328-1330 p.
- Сен-ди ю (D.У. Нsiеh). Некоторые аналитические аспекты динамики пузырьков.//Теоретические основы инженерных расчетов. М. Мир. №4. 1965 -157-173 с.


