Динамика кельтского камня при малом трении

Хорошо известно [1], что при вращении кельтского камня вокруг вертикальной оси направление этого вращения может изменяться в процессе движения. В большинстве работ, посвященных этому свойству, рассматривается неголономная постановка, задачи (см., например, [2, 3]). Однако, например, в работе [4] указывается на. физическую необоснованность данной постановки.

В настоящей работе продолжается исследование [2], в котором предполагается, что со стороны плоскости на камень действует сила классического вязкого трения. Эта модель трения позволяет провести не только численные [5], но и аналитические исследования.

• 1.    Постановка задачи

Рассмотрим задачу о движении тяжелого выпуклого твердого тела. на. неподвижной горизонтальной плоскости. Пусть v - скорость центр масс тела, ш - его угловая скорость, а д - единичный вектор восходящей вертикали. Тогда радиус-вектор точки контакта тела и плоскости определяется равенством д = -grad/( r )/|grad/( г )|/( г ) = 0 - уравнение поверхности тела, а скорость этой точки имеет вид u = v + [ш, г ].

Будем считать, что на тело действуют сила тяжести —тдд, нормальная компонента реакции опорной плоскости N = Nд и сила вязкого трения F = —ки. Уравнения движения тела, записанные в главных центральных осях тела (J = diag(Ai, A2, A3) - соответствующий тензор инерции), имеют вид mv + [ш,mv] = (N — тд)д + F,(1)

JШ + [ш, Jш] = [г, Nд + F],(2)

д + [ш, д ]=0,(3)

(и, д ) = °(4)

Уравнение (1) выражает теорему о движении центра масс тела, (2) - теорему об изменении кинетического момента относительно центра масс, (3) - условие постоянства вектора восходящей вертикали, а (4) - условие контакта тела с плоскостью.

Заметим, что если в процессе движения величина N изменит знак с положительного на отрицательный, то произойдет отрыв тела от опорной плоскости. В этом случае в качестве уравнений движения следует рассматривать (1)—(3), положив в них N = 0 и Ғ = 0 и добавив к ним уравнение % = (u, 7) (в момент отрыва и при возвращении на контакт % = 0). В случае же контакта тела с плоскостью из системы (1)-(4) определяется величина нормальной реакции

N = т (д + ([r, ш] + [Г, ш], 7) + ([ш, г], [ш, 7])),                       (5)

что позволяет считать систему (1)-(3) замкнутой относительно переменных v, ш и 7.

Будем считать, что положительная полуось Охз перпендикулярна поверхности тела. Тогда система (1)-(3) с учетом (5) имеет решения вида

• V1 = V2 = из = 0,  71 = 72 = 0,  7з = 1,  ші = ш2 = 0,   шз = ш (ш Е R),      (6)

• 2.    Движения в окрестности устойчивых равновесий

на которых величина нормальной реакции опорной плоскости равна весу тела. Им соответствуют равномерные вращения тела вокруг перпендикулярной его поверхности главной оси инерции, совпадающей с вертикалью. Уравнение поверхности тела при 73 = 1 можно представить в виде

(щ cos 5 + х₂ sin 5)2   (щ sin 5 — х₂ cos 5)2

/ (r) = хз + аз------------------+ Оз (Ж1,Ж2),         (7)

2аі                      2а2

где аі, а2 - главные радиусы кривизны поверхности тела в точке контакта, аз - высота центра масс, 5 — угол между векторами главных кривизн и главными осями. Рассматриваемое тело является кельтским камнем [2], если выполнены соотношения Аі = А2 , аі = а2, 5 = 0 (mod л/2).

Хорошо известны [2, 3] условия устойчивости решений (6) в случае неголономной постановки задачи, одним из которых является отрицательное направление вращения. В случае произвольного коэффициента вязкого трения линеаризованные уравнения возмущенного движения системы в окрестности решений (6) довольно громоздки [2] и аналитический анализ условий устойчивости затруднителен. Однако соответствующие области устойчивости при фиксированных параметрах задачи могут быть построены численно [5].

Будем считать, что параметры кельтского камня таковы, что соответствующие (6) равновесия устойчивы, т.е. без ограничения общности будем считать, что выполнены соотношения [2]:

аі > а2 > аз, J| < J2 < Уз.                                (8)

Тогда при любом коэффициенте вязкого трения в некоторой окрестности значения шз = 0 существует область устойчивости вращений (6). Например, для кельтского камня с пара- метрами

Аі = 0.0706 • 10^-3 кг^I², А2 = 0.443 • 10^-3 к г-аі², Аз = 0.49 • 10^-3 i сг-аі² аі = 0.74 м, а2 = 0.0666 м, аз = 0.00765 м, т = 0.1 ісг, 5 = 0.7 эта область представлена на рис. 1.

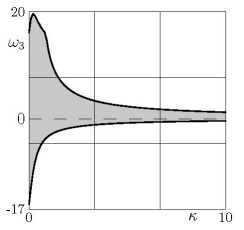
Рассмотрим движение в окрестности устойчивых равновесий, считая движение безотрывным. Тогда уравнения (1)-(3) с учетом (5) допускают интеграл (4) и геометрический интеграл (7,7) = 1, позволяющие исключить переменные О” и 73 и соответствующие им уравнения. Остальные уравнения запишем в виде

7 1 = -W2 +Г 1 ,

7 2 = W1 +Г 2 ,

Ш 1 = Д (7 2 0 3 - 0 ” 7 1 - Ь272) - Д ” (Ш 1 0 ” + 02) + О 1 , ^mg ,            , ,        , ,      .     Ааз ,                . ,

(Ю)

(И)

Ш2 = — (-7103 + 0372 + 0171)--— (Ш20” - щ) + О2, д 2                  Д

Г 1 = — (0 3 Ш2 - уД + V1, m«

Г 2 =-- (« 3 ^ 1 + Г 2 ) + V 2 ,

т

• ^А 1 ^{- А} 2        , ^mg /, / 9 7л м       х X .

Ш3 = —д--- Ш2Ш1 + д - (03 (7 1 ² - 7 22 ) - (0 1 - 0 2 ) 7 2 7 1) +

КШ” /0 1 0 2 (7 1 ² +7 22 ) (0 12 + 0 22 )

+—j— --------z--- —Ц7-------- - (0 1 7 1 ²+0 2 7 22 ) (0 1 +0 2 ) - 2 0” (0 1 +0 2 ) 7 1 7 2 +

А ” у        (О 1 + 0 2 )²

, ^д0 3

+"А"" (« 3 (Ш 2 7 1 +Ш 1 7 2 ) - (Г 1 7 1 -Г 2 7 2 )) + д ”

+ Д («3(01Ш171 + 02Ш272) + 01-0271 -02^172) , где

01 = 01 cos2 5 + о2 sin2 5,   02 = 01 sin2 5 + о2 cos2 5,   0” = («1 - 02) sin 5 cos 5, а Г/, О/ и V/ (г = 1, 2) функции, разложения которых по степеням переменных системы (10), (11) содержит только члены не ниже второго порядка этих переменных, а О” - члены не ниже четвертого.

Система (10) в случае Г/ = 0, О/ = 0 и V/ = 0 (г = 1, 2) замкнута и при к = 0 описывает малые колебания кельтского камня на абсолютно гладкой плоскости. Частоты этих колебаний (£1 > £2 > 0) являются корнями уравнения

Д 1 ^ 2 ^ 4 + mg (А 1 (0 1 - 0 3 ) + А 2 (0 2 - 0 3 )) £² + т²)²(о 1 - 0 3Д 0 3 - 0 2 ) = 0.

Рассмотрим замену переменных вида mg0”

71 = 91 cos ^2---.------7---—2 Р2 sin ^2, mg (01 - 03) - ДД2

mg0 ”

72 =--77------7---7-72 Р1 cos ^2 + Р2 sin У1, mg (02 - 03) - ДД2

^mg^ 2 ⁰ 3

Ш1 = ---ту------7---.—о Р1 sin ^2 + 41Р2 cos ^1, mg (02 - 03) - ДД2

^mg^ 1 ⁰ 3

Ш2 = 42Р1sin ^2 +--77------;---гтг Р2 cos ^1, mg (01 - 03) - Д2£і считая малым отклонение от равновесий (р/ ^ 1, Ш”/£/ ^ 1 (г = 1,2)) и коэффициент трения («/(m^/) ^ 1 (г = 1, 2)). Тогда в системе (10), (11), записанной в новых переменных без учета слагаемых Г/, О/, V/ (г = 1, 2) и О”, переменные р1 и р2 являются медленными, а д1 и д2 быстрыми. Величина Ш” при этом также является медленной переменной, т.к. в отсутствии трения решения уравнений движения выпуклого тела на гладкой плоскости являются условно-периодическими функциями времени [6] и первое слагаемое правой части (11) в среднем не меняется.

Считая нерезонансными значения £1 и (2 и осредняя указанные уравнения по быстрым переменным получим

/91 = -« 1 Р 1 ,      /92 = -« 2 Р 2 ,      сШ 3 = -(Др1 + ^2р2 ) Ш”,                (12)

где постоянные коэффициенты а/, ^/ (г = 1, 2) определяются равенствами

= «0 ” Л ₊__ m²g²0 2 (A/ - А ” -/) __________________________\

^{/   2А} ” -/ А 1 А 2 ^ 2 £ 2 - mg (А 1 £ 2 (0 1 - 0 3 ) + А 2 ^ 2 (0 2 - 0 3 )) + m²g²(0 1 - 0 ” )(0 ” - 0 2 ) ,

P_/ = [ (0² cos² 5 + 0 2 _-/ sin² 5)А_/²( ” _-/⁴ + (0 ! 0 2 - 20₁0₂0 ” 0_/ + 0 2 (0 2 sin² 5 + 0 2 _-/ cos² 5)) m²g²+

m² g²0 2 (4/

^{- А} 3 -/)

+ 2 (0 3 (0² cos² 5 + 0 2 _-г sin² 5) - 20 1 0 2 0/) А/ £ 3 —²gm] /(2Д 3 (mg (0 ” -/ - 0 3 ) - А/(2-^ )²).

Поскольку уравнения (12) не содержат переменных vi и V2, соответствующие уравнения не приводятся. Решая систему (12), получим

P1(t) = P1 (0) exp(-Qit), P2(t) = р2 (0) exp(-Q2t),

^ш3^(t) = шз^{(0) ex}p ^--;^- ⁽P1⁽⁰⁾2 ^- P1^{(t)2) -} у²- ⁽P2⁽⁰⁾2 ^- P2^(t)2)) . 2а1                    2а2

ТТ          Г1

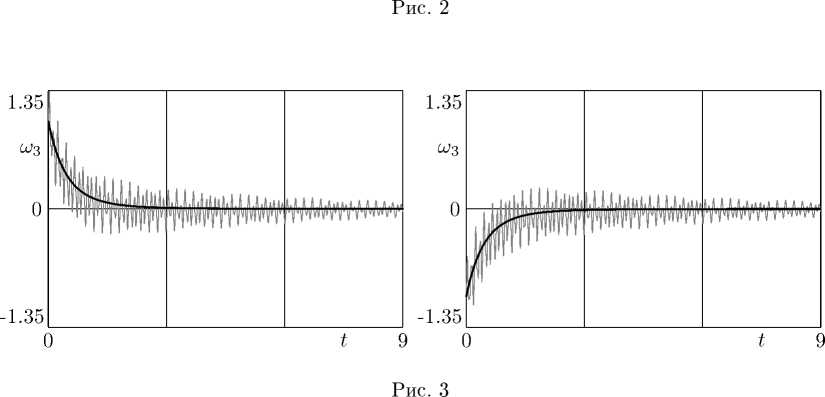
На рис. 2 представлены зависимости величины шз от времени при интегрировании урав нений (10), (11) (серые кривые) для кельского камня с параметрами (9) на плоскости с коэффициентом трения к = 0.4 кг/с при начальных условиях

73(0) = 0.99, 71 (0) = 0, шз(0) = ±15 рад/с, шД0) = Ш2(0) = 0, v(0) = 0 (величина 71(0) определялась геометрическим интегралом) и соответсвующая зависимость (13) (черные кривые).

На рис. 3 представлены те же результаты для меньшего значения начальной угловой скорости (шз(0) = ±1 рад/с). Как и следовало ожидать, решение точной системы представляет собой сумму плавно меняющейся медианы, хорошо совпадающей с решением осредненной системы и быстро осциллирующей затухающие компоненты. Заметим, что изменение абсо лютной величины шз в решении осредненной системы не зависит от ее знака, и существенных отличий в решениях точной системы при противоположных начальных направлениях вращения не наблюдается.

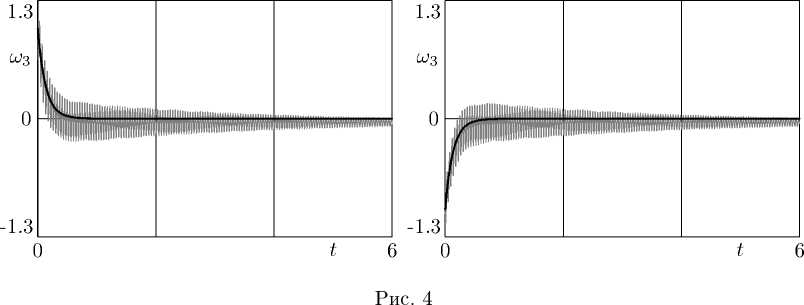
Следует отметить, что возможно отклонение среднего значения точного решения от решения осредненной системы (на величину первого порядка малости). Для тех же параметров задачи отклонение наблюдается (см. рис 4, 5) при начальных условиях

7з(0) = 0.97, шз(0) = ±1 рад/с, ші(0) = Ш2(0) = 0, v(0) = 0,

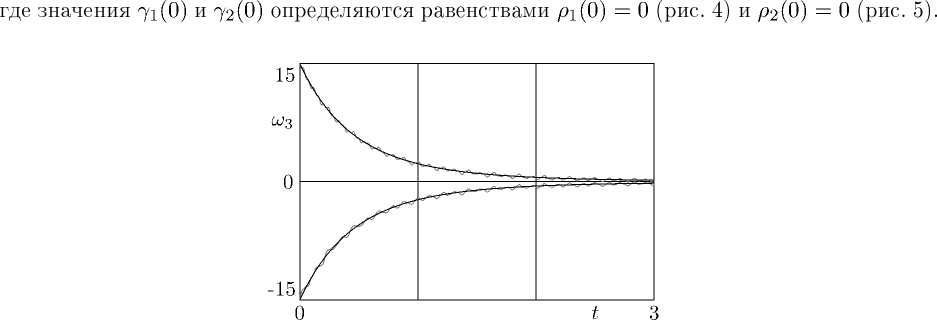
Таким образом, несмотря на то, что финальное значение шз решения усредненной системы (13) совпадает по знаку с начальным, соответствующее решение полной системы (10), (11) может поменять знак как с положительного на отрицательный, так и наоборот.

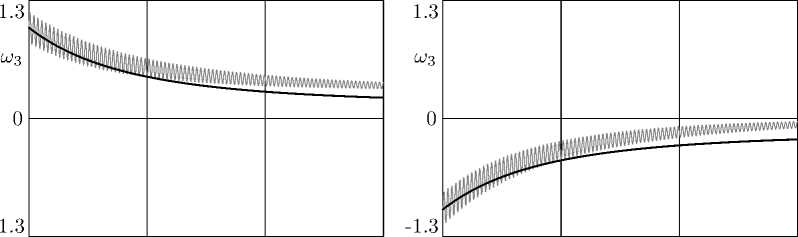
0                                  t 18     0                                  t 18

Рис. 5

Соответсвующие результаты при тех же начальных условиях, что и в предыдущем случае, но при к = 1 кг/с представлены на рис. Ь.

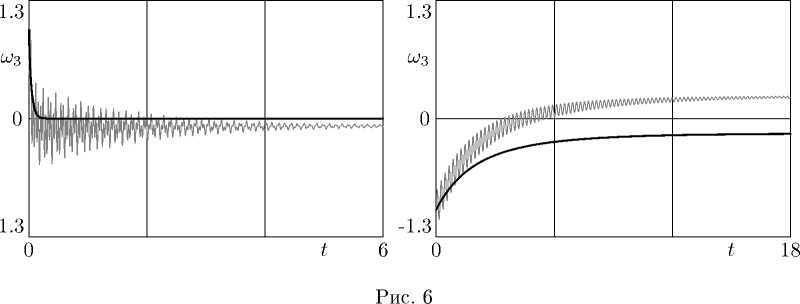
1.3

ω 3

-1.3

0                                    t 10

Кроме того, при интегрировании точных уравнений движения (10), (11) может наблюдаться несколько смен знака не только величины шз, но и ее среднего значения. Соответствующее решение при к = 3 кг/с представлено на рис. 7.

В заключение заметим, что при выполнении неравенств (8) резонанс ф = (2 невозможен. Но существуют такие параметры задачи, при которых величины £1 и (2 принимают относительно близкие значения, что позволяет при некотором классе начальных условий оценить финальное значение решения точной системы [7]. Кроме того, возможны случаи ^1/^2 € Q- Тогда осреденная система имеет аналогичный (12) вид и качественно динамика совпадает с рассмотренным случаем.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (19-01-00140, 18-01-00335) и Программы фундаментальных научных исследований по приоритетным направлениям, определяемым Президиумом Российской академии наук, № 7 «Новые разработки в перспективных направлениях энергетики, механики и робототехники».