Динамика коэффициента корреляции при манипулировании геологическими совокупностями

Корреляционно-регрессионный анализ со времен К. Пирсона [8] (примерно с 1900 г.) стал одним из важных эвристических методов, позволяющих с заданной доверительной вероятностью установить наличие зависимости между признаками и её форму. В дальнейшем методы установления связи значительно усовершенствовались: появились ранговые коэффициенты корреляции в варианте К. Спирмена, а затем и М. Кендалла, не требующие для установления зависимости количественных данных. Наконец для номинативных (классификационных) признаков (красный, синий, голубой, зеленый, тяжелый, легкий, кварцевый, сульфидный, сульфатный и т. д.), которые невозможно даже ранжировать, А. А. Чупровым (1960) был предложен коэффициент сопряженности признаков , так называемый полихорический коэффициент . Для случая альтернативных признаков ( да, нет , наличествует какой-либо признак или отсутствует) был предложен тетрахорический коэффициент сопряженности .

Классический (пирсоновский) коэффициент позволяет оценить не только силу связи, но и её форму: линейная, нелинейная, а в случае линейности — коэффициенты уравнения регрессии. Ранговый коэффициент корреляции позволяет установить, является ли связь прямой или обратной, т. е. увеличиваются ли значения одного признака с увеличением другого или уменьшаются, но не более того. Коэффициенты корреляции, основанные на номинативных признаках, позволяют установить только наличие связи или отсутствие таковой.

Значительное место в литературе, посвященной корреляционно-регрессионному анализу, уделено формальной и содержательной интерпретации уравнений регрессии. В результате дискуссий было установлено, что уравнения регрессии являются источником 6

информации о значении одной переменной по значениям другой, причем количество информации, которую несет переменная Х (предиктор) для оценки Y (предиктант), в точности равна информации, которую несет Y как предиктор, для оценки X .

Автор данной статьи в свое время разработал концепцию уравнения регрессии как инструмента оценки предиктанта из двух источников информации: а) конкретного значения предиктора, б) среднего значения переменной-предиктанта в изучаемой совокупности случайных величин [1, 2]. Из неё, в частности, следует, что при одной и той же содержательной (физической, химической, механической и т. д.) основе зависимости уравнения регрессии будут различными (и предсказуемыми!) для разных совокупностей случайных величин. Например, если совокупность состоит из элементов, в которых размах колебаний переменной-предиктора Х будет меньше, то коэффициент корреляции между Y и Х будет меньше, а график урaвнeния регрессии будет положе.

Разновидностью корреляционно-рeгрeссионного анализа стал позже разработанный конфлюэнтный анализ , в котором коррелирующие вeли-чины измерены с известными погрешностями и отыскивается нe урaвнeние регрессии, а так называемое структурное уравнение , одинаковое независимо от того, является ли предиктором Х или Y .

При значительной разработанности методов корреляционно-рeгрeссион-ного и конфлюэнтного анализов в их применении имеется большой пробел, связанный с интерпретацией результатов, в зависимости от того, что из себя представляет совокупность исходных данных. В частности, каков будет результат корреляционно-рeгрeссионно-го анализа в подсовокупности исходной совокупности, в которую мы отобрали пробы (элементы совокупнос- ти) по какому-либо признаку, нaпри-мер, по значениям X и/или Y, как теперь интерпретировать полученные результаты, что в них содержательного, а что является артефактами (лат. arte искусственно + factus сделанный), вольно или невольно порожденными процедурно-математическими свойствами корреляционно-рeгрeссионно-го анализа? Эта проблема весьма актуальна, так как гeологи и геохимики весьма часто варьируют смыслом изучаемых генеральных совокупностей и способом получения выборок из них, не всегда отдавая себе отчет в том, правильно ли они интерпретируют получаемые результаты.

Статья посвящена исследованию аналитическими методами и методами компьютерного моделирования следующих вопросов:

• 1.    Как изменится коэффициент корреляции и параметры урaвнeния регрессии в выборке, образованной из исходной совокупности селекцией проб:

• 2.    Каким будет коэффициент корреляции и параметры урaвнения регрессии, если коррелировать среднее содержание какого-либо компонента с его средним квадратическим отклонением? как эти параметры изменятся, eсли распределение компонента подчиняется:

а) с помощью случайного выбора, б) с помощью неслучайного выбора — в заданном интервале содержаний одного из двух коррелирующих компонентов, (нaпример, селекцией проб, содержание компонента в которых или выше заданного, или ниже заданного, или близко к среднему),

в) в заданном интервале (как в п. “б”) суммы содержаний обоих коррелирующих компонентов.

• а)    нормальному (Гауссовскому) закону,

• б)    логарифмически-нормальному закону.

• 3.    Как будет изменяться коэффициент корреляции и уравнение регрессии между двумя положительно или отри-

  
  
  

цательно коррелирующими или некоррелирующими величинами в выборках, пробы которых содержат ряд других компонентов, находящихся между собой в зависимостях, определяемых заданной корреляционной матрицей. Как будет изменяться коэффициент корреляции при изменении содержаний этих других (“фоновых”) компонентов?

Методика компьютерного моделирования

Основой компьютерного моделиро- вания в рассматриваемом случае является получение совокупности n проб, содержащих m компонентов с заданны- ми средними, средними квадратическими отклонениями и с заданной корреляционной матрицей. Никакой пробле- мы не возникает, если компонентов два: n = 2, x и y. Тогда с помощью датчика псевдослучайных чисел генерируется три нормально (или логнормально) распределенных независимых случайных числа: u, ε1 и ε2. С их помощью образу- ется пара чисел x = u + ε1,            (1)

y = u + ε ₂.            (2)

Коэффициент корреляции r_xy в этом случае будет равен в соответствии с работой [2]

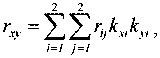
где rij — коэффициент корреляции между слагаемыми, составляющими x и y; в нашем случае ruu = 1, ruε1 = 1, ruε2 = 1, rε1ε2 = 1;           ,

,

О',

откуда

(остальные сла-

гаемые равны нулю, так как равны нулю коэффициенты корреляции между ними).

Далее,

'          <7 х<7 v где                 ,.

Если мы моделируем величины с нулевыми средними и единичными дисперсиями, то          и, притом ε1 = ε2 = ε, откуда

.

Таким образом, для моделирования двух случайных величин x и y необходимо получить три случайные величины u, ε1, ε2 c дисперсиями          со ответственно.

Описанное получение пары случайных величин x_i , y_i производится n раз

(по числу проб). Затем средние и дисперсии преобразуются в величины, распределенные со средними m_x, m_y и средними квадратическими отклонениями s_x и s_y , по формулам

,

.

Если требуется моделировать содержания , т. е. величины положительные , то m_x и m_y следует выбирать достаточно большими, например m_x > 3s_x , m_y > 3s_y , и цензурировать моделируемые величины по условию , , т. е. отбрасывать отрицательные величины. При m_x > 3s_x , m_y > 3s_x таких величин будет сравнительно немного, 0.13 %.

Замоделировать совокупность с m произвольно коррелирующими компонентами значительно сложнее. Не всякая придуманная корреляционная матрица является непротиворечивой . Уже при трех переменных два коэффициента корреляции могут быть выбраны произвольно, а третий предопределен, точнее — ограничен интервалом, который сужается по мере увеличения абсолютных значений двух первых коэффициентов.

При большом числе компонентов дело значительно усложняется. Произвольно составленная корреляционная матрица имеет весьма малую вероятность быть непротиворечивой. В связи с этим для решения некоторых задач (как наша) компьютерным моделированием лучше выбрать за основу какую-либо реальную корреляционную матрицу и определять остаточные дисперсии, т. е. дисперсии некоррелирующих слагаемых типа ε ₁, ε ₂ в равенствах (1), (2) решением системы уравнений

( t, q = 1..m )

относительно k_x, k_y при r_ij = 1 для общего слагаемого суммы и r_ij = 0 — для остальных.

Полученная исходная двух- или многокомпонентная совокупность при этом еще не будет замкнутой системой процентных величин. При необходимости анализа замкнутой системы процентных величин она преобразуется в таковую простым пересчетом так, чтобы сумма компонентов в каждой пробе составляла 100 %. Далее из этой выборки формируются подвыборки по одной из намеченных выше схем и по этим подвыборкам стандартными процедурами корреляционно-регрессион- ного анализа определяются коэффициенты корреляции и параметры уравнений регрессии.

Результаты теоретического анализа и компьютерного статистического моделирования

• 1.    Изучение динамики r, a и b в случайных выборках из генеральной совокупности двумерных элементов (система не является замкнутой процентной системой).

• 2.    Изучение динамики r, a и b в неслучайных выборках из той же генеральной совокупности, что и в п. 1.

Очевидно, что и коэффициент корреляции r , и параметры уравнений регрессии a и b в таких выборках будут несмещенными оценками этих величин в генеральной совокупности. В соответствии с теорией, флуктуации значений r, a, и b будут тем больше, чем меньше объем выборки, а именно

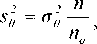
где — дисперсия какого-либо из перечисленных выше параметров и в выборке объема n_o , — её значение в конечной генеральной совокупности объёма n .

Приведенные в табл. 1 результаты полностью следуют теории. Это обстоятельство настолько очевидно и было предсказуемо, что, можно сказать, этот эксперимент мы проводили скорее для того, чтобы убедиться (и убедить читателей) в корректности алгоритма и программы моделирования.

В частности, в выборку отбирались: а) сначала все пробы, значения величины x в которых превышали некоторое установленное значение, б) затем все пробы, в которых значения x были ниже некоторого значения, в) пробы, значения x в которых заключены в некотором интервале вблизи среднего значения, г) наконец, пробы, значения x + y в которых были выше, ниже и в середине заданных значений этой суммы в генеральной совокупности. Необходимость изучать неслучайные выборки по критерию суммы x + y возникла для того, чтобы в минимальной степени искажать корреляционный эллипс отсечением части проб: отсечение должно также производиться прямой, перпендикулярной длинной оси эллипса.

Во всех этих случаях по теории должно наблюдаться уменьшение коэффи-

Таблица 1 терпретировать в геохимическом или

Иллюстрация постоянства коэффициента корреляции при формировании каком-либо другом содержательном выборок случайным образом (первая строка каждой секции таблицы — смысле. заданная генеральная совокупность) Исследование выборок, полученных п 300 Г 0.86 1 а 0.81 b -0.06 п 1000 г        | 0.50 а 0.50 b 0.01 селекцией из генеральной совокупности по сумме x + y показало ещё более яркую картину (см. табл. 3 — селекция 90 0.85 0.79 -U.U6 300 0.44 0.45 0.03 по средним значениям x + y, табл. 4 — 72 0.84 0.75 -0.13 240 0.49 0.49 0.13 селекция по низким значениям суммы 54 0.80 0.77 -0.05 180 0.50 0.49 0.01 x и y). 3. Исследование коэффициента 36 0.76 0.72 -0.18 150 0.41 0.44 0.03 18 0.85 0.96 0.01 90 0.52 0.54 0.19 корреляции между средним значением 1000 0.79 0.81 0.00 1000 0.32 0.32 -0.01 случайной величины и её средним квад- 300 0.80 0.80 -0.03 300 0.32 0.32 0.04 ратическим отклонением. 270 0.78 0.77 0.03 240 0.26 0.25 0.09 Вообще говоря, в различных сово- 210 0.80 0.84 -0.08 180 0.29 0.28 0.05 купностях между этими величинами 150 0.78 0.85 0.08 150 0.38 0.38 -0.14 нет никакой связи. Большие содержа- 90 0.81 0.82 0.04 90 0.21 0.22 -0.11 ния могут слабо флуктуировать, а в 300 0.57 0.57 -0.01 300 0.29 0.29 0.11 других случаях наоборот — малые со- 90 0.61 0.63 -0.14 90 0.40 0.37 0.10 держания могут варьировать значи- 81 0.42 0.42 0.04 72 0.44 0.42 0.03 тельнее. Но здесь речь пойдёт об од- 63 0.61 0.61 -0.01 63 0.27 0.26 0.02 ной совокупности заданным образом 36 0.56 0.56 0.10 54 0.28 0.22 0.20 (нормально или логнормально) рас- 27 0.54 0.50 0.08 45 0.34 0.30 0.04 пределенных величин. Эта совокупность разбивается на ряд подсовокуп- циента корреляции r и уменьшение наклона графика уравнения регрессии (т. е. уменьшение a). Это следует из того, что коэффициент корреляции можно выразить через дисперсии следующим образом:

„2 _ у_ Оцстх _ 7 _ осту

, Оу где — дисперсия величины x в совокупности (или в подсовокупности), т. е. величина, характеризующая “длину” корреляционного эллипса; — остаточная дисперсия величины x, т. е. величина, характеризующая “толщину” корреляционного эллипса; ,    — те же параметры, но в отношении величины y.

Поскольку в любой выборке из заданного интервала значений x (или y ) длина корреляционного эллипса уменьшается, а толщина — нет, то r будет уменьшаться (и даже менять знак с плю-

О х са на минус). Так как          , то с а х уменьшением r уменьшится и a — угловой коэффициент графика уравнения регрессии.

Моделирование выборок селекцией проб с высокими значениями величины x из генеральных совокупностей с различными исходными значениями r_xy подтвердило правильность теории (табл. 2). Оно наглядно показало, что уменьшение r_xy и a_yx является типичным артефактом, который нельзя ин-

Таблица 2

Динамика коэффициента корреляции по данным компьютерного моделирования выборок из верхней части совокупности 1000 проб (первая строка каждой секции таблицы — генеральная совокупность)

п	г	а	ь	п		а	ь
1000	0.90	0.90	1.04	1000	0.79	0.80	0.01
300	0.55	0.31	0.86	300	0.47	0.61	0.24
240	0.47	0.22	1.05	270	0.53	0.70	0.11
180	0.37	0.15	1.22	210	0.49	0.64	0.21
150	0.21	0.08	1.35	180	0.46	0.58	0.30
90	0.20	0.04	1.51	120	0.44	0.51	0.43
1000	0.80	0.82	-0.00	1000	0.49	0.48	-0.63
300	0.48	0.61	0.24	300	0.52	1.11	-0.84
240	0.46	0.56	0.33	240	0.51	1.10	-0.84
180	0.47	0.59	0.28	150	0.53	1.14	-0.90
90	0.51	0.66	0.17	60	0.43	0.91	-0.46
30	0.23	0.28	0.92	30	0.33	0.59	0.16

Таблица 3

Динамика коэффициента корреляции по данным компьютерного моделирования из совокупности 1000 проб селекцией по сумме значений коррелирующих величин (из средней части совокупности 1000 проб) (первая строка каждой секции таблицы — генеральная совокупность)

п	г	а	b	И	г	а	ь
1000	0.90	0.92	0.05	1000	0.45	0.46	-0.01
300	0.28	0.29	0.05	300	-0.74	-0.84	-0.01
270	0.17	0.17	0.06	270	-0.78	-0.89	-0.01
240	0.08	0.08	0.06	240	-0.82	-0.91	-0.01
210	-0.06	-0.06	0.07	210	-0.86	-0.93	-0.01
180	-0.21	-0.22	0.08	180	-0.90	-0.99	-0.01
150	-0.38	-0.37	0.09	150	-0.93	-1.02	-0.01
120	-0.55	-0.49	0.09	120	-0.96	-1.01	-0.01
90	-0.74	-0.65	0.09	90	-0.97	-1.04	-0.01
60	-0.86	-0.85	0.10	60	-0.99	-1.04	-0.02
30	-0.96	-0.98	0.11	30	-1.00	-1.02	-0.02

Таблица 4

Динамика коэффициента корреляции по данным компьютерного моделирования выборок из совокупности 1000 проб селекцией по сумме значений коррелирующих величин (нижняя часть совокупности) (первая строка слева — генеральная совокупность)

п	г	а	ь	И	г	а	ь
1000	0.90	0.92	0.05	150	0.06	0.04	-1.34
300	0.34	0.26	-0.88	120	0.02	0.01	-1.41
270	0.28	0.20	-0.98	90	0.06	0.04	-1.39
240	0.25	0.17	-1.05	60	0.07	0.06	-1.43
210	0.18	0.12	-1.15	30	0.00	0.00	-1.61
180	0.12	0.08	-1.23

ностей по увеличению значения x. В каждой такой подсовокупности определяется среднее значение mx и среднее квадратическое отклонение σx. Исследуется вопрос о том, каков будет коэффициент корреляции между mx и σx и как он будет зависеть от вида распределения x. Рассмотрим нормальное распределение. Разделим трех-четы-рехсигмовый диапазон значений x на 9—11 равных интервалов. Средние значения переменной в каждом интервале близки к середине интервала (а в среднем интервале совпадает с ним). Дисперсии в интервалах, равно удаленных от среднего, равны, так как распределения в этих интервалах симметричны. Этого достаточно, чтобы убедиться в отсутствии корреляционной зависимости между mx и σx: с увеличени ем mx среднее квадратическое отклонение (относительно интервального среднего!) сначала увеличивается при движении к левому “односигмовому” интервалу, затем убывает к серединному интервалу, затем снова увеличивается к правому односигмовому интервалу и вновь уменьшается к правому хвосту распределения. При такой “раскладке” никакой корреляции между mx и σx быть не может: σx при всех значениях mx приблизительно сохраняет свое значение на уровне , где h — ши- рина интервала.

При логарифмически-нормальном распределении это утверждение относится к логарифмам величин: среднему значению логарифма и логарифмической дисперсии, что при потенцировании приводит к сильнейшей корреляции между частным (интервальным) средним и антилогарифмом дисперсии (соответственно, и средним квадратическим). Это и понятно: равные в логарифмах интервалы при потенциро- вании сильно растягиваются при движении по числовой оси вправо, приводя к увеличению дисперсии. Этот факт, впрочем, был давно замечен как в отношении природной изменчивости [2], так и в отношении погрешностей измерений [3].

Моделирование показало, что, действительно, при нормальном (Гауссовом) распределении никакой зависимости между m_x и σ _x не наблюдается, тогда как при моделировании логарифмиче-ски-нормального распределения эта зависимость наблюдается, и притом сильная ( r близок к единице):

среднее	0.31	0.47	0.54	0.72	0.80	1.06	1.21	Если нас интересует ди-
ср. кв. откл.	0.02	0.02	0.03	0.02	0.03	0.04	0.05	намика r только между дву-
среднее	1.60	1.89	2.54	3.20	4.56	8.91		мя выделенными нами ком-
ср. кв. откл.	0.09	0.07	0.15	0.25	0.57	3.03		понентами, то сумму всех
								оставшихся можно считать
коэф. кор.	0.91							третьим компонентом. Если

Это наглядно видно и на рис. 1.

4. Исследование динамики коэффициента корреляции в замкнутой сис-

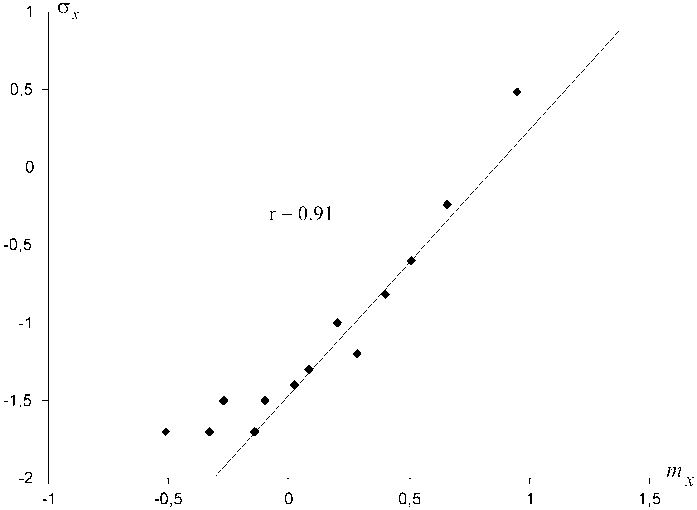
Рис. 1. Зависимость между средним (m_x) и среднеквадратическим отклонением (σ_x) при моделировании логарифмически нормального распределения.

теме процентных величин при увеличении содержаний двух избранных компонентов на фоне уменьшения содержаний остальных компонентов.

Еще К. Пирсон [8] более ста лет назад указывал на появление ложной корреляции в системе процентных величин. Настоящий бум интереса к этой проблеме породили работы Ф. Чейза [4, 5], известного петрографа и минералога. Его исследования показали следующее: а) в закрытой системе из n ‒ 1 коэффициентов корреляции каждой строки корреляционной матрицы по крайней мере один отрицателен; б) из общего числа

коэффициентов кор-

реляции по крайней мере n ‒ 1 отрицательны; в) в трехкомпонентной системе, если никакая дисперсия не превышает суммы двух остальных, то все три r будут отрицательны; г) компонент с максимальной дисперсией имеет отрицательные коэффициенты корреляции по крайней мере с двумя из остальных компонентов. В дальнейшем эти результаты были развиты в работах [6, 7, 9], а также [1].

уменьшать содержание этого третьего (суммарного) компонента, то это автоматически приведет к уменьшению

его дисперсии и, как следствие, к тому, что дисперсия одного из выделенных компонентов станет самой большой. По крайней мере с этого момента (но может, и значительно раньше) коэффициент корреляции между выделенными компонентами станет отрицательным.

Нам удалось найти наглядную графическую форму доказательства этого положения и неизбежности стремления коэффициента корреляции двух выделенных компонентов к значению ‒1 при уменьшении содержания остальных. Пусть между выделенными компонентами (например, Fe и Mn) существует положительная корреляционная зависимость. Тогда на графике (см. рис. 2) “облако” точек в координатах Fe‒Mn будет представлять собой облако точек, вытянутое вправо-вверх. Проведем на этом графике дополнительную прямую, соединяющую точки (100 % Fe, 0 % Mn) и (0 % Fe, 100 % Mn).

При относительном увеличении содержания выделенных компонентов без изменения их соотношения (например, путем уменьшения суммы других (фоновых) компонентов) точки графика будут смещаться радиально от начала координат, приближаясь к прямой Fe + Mn = 100 %. Скорость этого смещения (при одинаковом темпе увеличения содержания) будет уменьшаться, так что точки в конце концов лягут на прямую с координатами (100 % Fe, 0 % Mn), (0 % Fe, 100 % Mn), а это означает, что коэффициент корреляции между этими компонентами станет равным ‒1. При этом неважно, каким способом реализуется уменьшение содержания “фоновых” компонентов: специальной подборкой ли выборок из огромной природной генеральной совокупности объектов, химической ли обработкой проб одной и той же выборки (растворением карбонатной части проб, озолением проб углей нефтей и горючих сланцев и т. д.). В зависимости от того, с какой скоростью относительно друг друга точки будут радиально удаляться от начала координат, изменение r может быть различным. например, в процессе этого передвижения “положительный” эллипс может постепенно превратиться в “нейтральный” круг, а затем вытянуться длинной осью параллельно указанной прямой Fe + Mn = = 100 %, что будет соответствовать отрицательной корреляции, и, наконец,

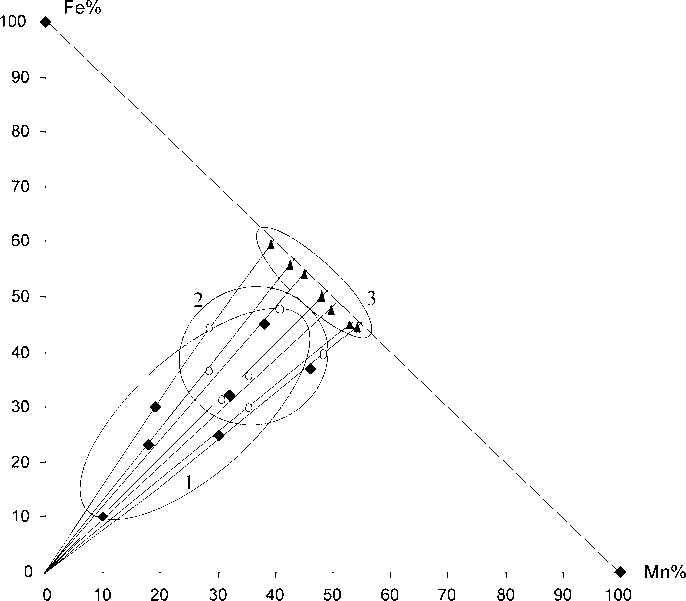
Рис. 2. Радиальное от начала координат движение точек-проб при уменьшении содержания в них суммы “фоновых” компонентов.

Квадратики — “начальное” положение точек, характеризуемое корреляционным эллипсом 1 (r = 0.7); кружки — положение точек при уменьшении содержания фоновых компонентов в среднем с 45 % до 25 %, корреляционный эллипс превратился в круг 2 (r = 0.0)

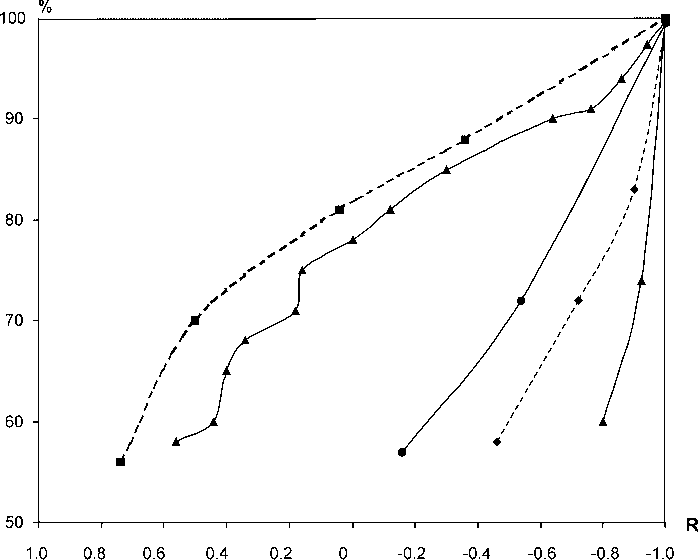
Рис. 3. Зависимость коэффициента корреляции от суммы содержаний в процентной системе (исходный коэффициент корреляции между Fe и Mn в условно открытой системе равен +1.0)

когда все точки лягут на эту прямую, коэффициент корреляции станет равным ‒1, угловой коэффициент прямой регрессии станет также равным ‒1. Такая модель реализуется в том наиболее вероятном случае, когда убывание фона будет пропорциональным его текущему содержанию. Может встретится случай, когда убывание фона в абсолютных процентах одинаково во всех пробах. Тогда корреляционный эллипс сначала вытянет- ся и коэффициент корреляции увеличится, но по мере того, как всё большее число точек попадет на прямую Fe + Mn = 100 %, коэффициент корреляции станет уменьшаться и быстро достигнет значения ‒1.

Единственный исключительный и маловероятный случай может возникнуть тогда, когда еще при малом содержании суммы выделенных компонентов коэффициент корреляции между ними был равен +1 при равенстве содержаний x и y . Тогда точки графика будут лежать в точности на прямой x = y , и при уменьшении содержания фоновых компонентов “стрела” точек будет перемещаться вдоль своего направления, и когда x + y достигнет 100 %, все точки сольются в одну: вариации содержаний не будет, и коэффициент корреляции потеряет смысл (выродится).

Результаты моделирования закрытой системы, представленные в табл. 5 полностью подтвердили приведенные теоретические рассуждения. На рис. 3 приведены кривые приближения коэффициентов корреляции к значению ‒1 в зависимости от “начального” коэффициента корреляции, т. е. от того, который наблюдался бы при очень сильном разбавлении системы фоновыми компонентами. Модель уменьшения “фона” выбрана пропорциональной текущему содержания фона.

Таким образом, превращение положительного коэффициента корреляции в отрицательный, в итоге равный ‒1 при уменьшении до нуля содержания всех остальных компонентов, является артефактом и не подлежит никакой содержательной интерпретации.

При моделировании выявился еще один любопытный феномен. Если коэффициент корреляции в не закрытой, не процентной системе между выделенными компонентами близок или равен ‒1, то дисперсия их суммы равна

, т. е. весьма мала (или равна нулю при sx = sy), и пересчет на закрытую систему сильно увеличивает этот коэффициент при условии, что дисперсия суммы фоновых компонентов больше, чем (sx ‒ sy)2. Этот феномен известен геохимикам, занимающимся породами с большим количеством разбавителя, например углей, когда поведение элементов рассматривается либо в пересчете химических элементов на золу, либо в целом на уголь;

Таблица 5

Динамика коэффициента корреляции при уменьшении суммы содержаний “фоновых” компонентов

Содержание фоновых компонентов	№ моделирования	Мп%	Fe%	(Mn+Fe)%	Г
	1	29.1	28.6	57.7	66.1
~ 43%	2	23.1	27.9	51.0	73.4
	3	32.0	29.9	61.9	76.4
	4	28.3	28.9	57.2	47.2
	10	29.1	27.5	56.6	61.0
среднее из 10		28.2	28.8	57.0	66.0
	1	37.0	36.9	73.9	34.8
~ 29%	2	34.2	32.6	66.8	34.3
	3	35.7	35.4	71.2	56.3
	4	38.7	37.7	76.5	-11.9
	10	33.5	32.8	66.3	44.2
среднее из 10		35.3	35.9	71.3	28.7
	1	43.6	46.1	89.7	-60.0
~ 11%	2	45.4	43.1	88.5	-65.1
	3	43.7	47.4	91.2	-51.0
	4	44.1	43.5	87.6	-55.2
	10	45.4	44.7	90.0	-42.3
среднее из 10		44.0	44.9	88.9	-54.9

	1	46.7	49.3	96.1	-84.6
~4%	2	49.6	48.0	97.6	-96.5
	3	48.9	48.0	96.9	-97.3
	4	47.1	47.7	94.8	-75.3
	10	50.2	47.2	97.4	-98.0
среднее из 10		48.4	47.9	96.3	-87.4
	1	47.6	51.6	99.2	-99.7
~ 1%	2	49.5	49.7	99.2	-99.7
	3	50.2	48.8	99.0	-99.7
	10	49.8	48.8	98.6	-91.8
среднее из 10		48.9	50.1	99.1	-98.7

известняков, когда то же самое делается в пересчете на нерастворимый остаток или на всю карбонатную породу. В золе или нерастворимом остатке часто наблюдаются отрицательные коэффициенты корреляции между компонентами. При пересчете на всю породу именно из-за большой дисперсии содержания органики (или карбонатной части) — отрицательные корреляции превращаются в положительные. Парадоксальный феномен получил теоретическое объяснение и подтверждён компьютерным моделированием, следовательно, перестал быть парадоксальным.