Динамика нелинейных параметров электромиограммы ребенка в течение первых суток жизни

Этап раннего неонатального развития является одним из самых драматичных и важных периодов в жизни человека, поскольку в это время определяется функционирование физиологических систем на дальнейшие годы. Новорожденный в течение первых дней жизни проходит целый ряд транзиторных состояний разных органов и систем. В течение первых часов жизни он испытывает родовой катарсис, который сопровождается выбросом в кровь многочисленных гормонов [8]. После рождения одними из самых заметных изменений среды для ребенка являются появление гравитации и снижение температуры среды, что должно отразиться на функциональном состоянии двигательной системы. Новорожденный ребенок проходит стремительную адаптацию к новым условиям обитания, переживает своего рода «сенсорную атаку». В определенном смысле, плод является моделью организма в состоянии гипогравитации (иммерсия в плодных водах). Соответственно, ребенок после 270–280 дней

нахождения в утробе матери может служить аналогом человека, вернувшегося из длительного полета в условия земной гравитации. В этой связи нам представлялось интересным и важным исследовать электромиограмму (ЭМГ) новорожденного ребенка первых суток жизни. Известно, что ЭМГ отражает функциональное состояние двигательной системы и представляет собой нелинейный процесс [10]. Учитывая потенциальную диагностическую ценность некоторых новых нелинейных методов анализа интерференционной электромиограммы (иЭМГ), таких как рекуррентный и фрактальный анализ [11], [12], мы оценили временную структуру иЭМГ новорожденного в возрасте от 30 мин до 24 ч.

МЕТОДИКА

Исследовано 37 здоровых новорожденных детей (17 девочек, 20 мальчиков) со сроком гестации 38–40 недель, обладающих всеми признака- ми доношенности и зрелости. Все дети имели оценку по 10-балльной шкале Апгар 8/9 баллов. Группы детей по возрасту: I. 30 мин – 6 ч (n = 14), II. 6–12 ч (n = 6), III. 12–18 ч (n = 5), IV. 18–24 ч (n = 12). Согласно международным требованиям, у матерей было получено информированное согласие на участие в исследовании. Исследование проводилось на базе роддома им. Гуткина г. Петрозаводска в апреле – июне 2009 года на основании разрешения республиканского этического комитета. Спонтанная мышечная активность ребенка записывалась при спокойном бодрствовании в дневное время, до кормления грудью.

Поверхностную иЭМГ регистрировали с двух пар мышц-антагонистов ( m. biceps br. и m. triceps br . справа, m. tibialis ant . и m. gastrocnemius слева). Использовали электромиограф Нейро-МВП-8 c программной средой Нейрософт (ООО «Нейрософт», г. Иваново, Россия). Исследование выполняли 2 человека (один из них – врач-педиатр). К коже ребенка прикасались электродом, обработанным антисептиком. Кожу ребенка не обрабатывали, на электрод наносили гель. Руки обрабатывались антисептиком, исследование проводили в одноразовых халатах. Ребенок находился в своей кроватке, укрытый пеленкой. Исследование длилось 5–7 мин и не вызывало видимых признаков дискомфорта. Полоса пропускания ЭМГ составила 50–500 Гц. Регистрировали отрезки ЭМГ длительностью 1 с. Учитывая возможность влияния амплитуды ЭМГ на нелинейные параметры, разделяли полученные образцы ЭМГ на несколько групп: 1–25 мкВ, 25– 50 мкВ, 50–75 мкВ, 75–100 мкВ.

В математическом аспекте иЭМГ является временным числовым рядом, отражающим суммарную биоэлектрическую активность мышцы, и характеризуется аттрактором [12]. Аттрактор – это множество точек в фазовом пространстве динамической системы, к которым стремятся траектории системы [6].

Для динамических систем принятым представлением развития процесса во времени является построение «портрета» в фазовом пространстве (фазовый портрет). Наименьшее число независимых переменных, однозначно определяющее установившееся движение динамической системы, называют размерностью вложения m . Аттрактор характеризуется несколькими параметрами: корреляционная размерность ( D c ), корреляционная энтропия ( К 2 ) и фрактальная размерность ( D ).

Корреляционную размерность Dc и корреляционную энтропию К2, которые являются производными корреляционного интеграла, рассчитывали по методу Такенса [6], [9]. Корреляционная размерность Dc определяет степень сложности поведения динамической системы. Корреляционный интеграл рассчитывали по программе Fractan 4.4 (РАН) [6]. Размерность m в пространстве, начиная с которой Dc перестает изменяться, есть минимальная размерность вложения, то есть наименьшая целая размерность пространства, содержащего весь аттрактор. Она соответствует числу независимых переменных, описывающих систему, то есть отражает сложность управления системой. В случае с иЭМГ – сложность управления двигательной системой. Из этого следует возможность разграничить динамическую систему со сложным поведением (но характеризующуюся конечным m) и случайный шум, который теоретически описывается бесконечно большим числом независимых переменных. Так как количество уровней управления мышечным тонусом должно быть конечным, мы относим иЭМГ к сложным динамическим процессам.

Следующей характеристикой фрактальных свойств объекта является корреляционная энтропия К 2 , или информационная размерность. К 2 является мерой потери информации о системе во времени. Фактически К 2 является количественной характеристикой степени хаотичности системы, а также того, как быстро система становится непредсказуемой.

Фрактальная размерность D позволяет оценить внутренние взаимосвязи нелинейного процесса, в нашем случае – иЭМГ. D позволяет судить о сложности взаимосвязей и предсказуемости иЭМГ. Существуют различные способы определения фрактальных размерностей, к числу которых относится так называемый R/S-способ , на основании которого определяется показатель Херста [7]. Этот показатель очень устойчив и содержит минимальные предположения об изучаемой системе, поэтому он может классифицировать временные ряды. Для сравнения различных типов временных рядов Херст ввел следующее соотношение:

R/S = (aN)Н, где R/S – нормированный размах от накопленного среднего, N – число наблюдений, а – некоторая константа, Н – показатель Херста.

Фрактальная размерность рассчитывается по формуле:

D = 2-H, где Н – показатель Херста.

Фрактальная размерность временного ряда, или накопленных изменений при случайном блуждании, равна 1,5. Размерность линии – 1, а размерность геометрической плоскости – 2. Соответственно, фрактальная размерность случайного блуждания лежит между линией и плоскостью. Если Н = 0,5, то D = 1,5. Обе величины характеризуют независимую случайную систему. Величина 0,5 < Н ≤ 1 будет соответствовать фрактальной размерности, более близкой к кривой линии. Это персистентный временной ряд, дающий более гладкую, менее зазубренную линию, нежели случайное блуждание. Антиперсистентная величина Н (0 < Н < 0,5) дает соответственно более высокую фрактальную размерность и более прерывистую линию, чем случайное блуждание, и, следовательно, характеризует систему, более подверженную переменам.

Можно выделить 3 основных группы временных рядов, а также типов иЭМГ по фрактальной размерности [2]:

• 1.    Персистентная иЭМГ (D = 1–1,5). Cобытия на такой иЭМГ будут носить устойчивый характер: будут повторяться и/или нарастать. Чем ближе значения к 1, тем более выражены тенденции, тем меньше у ЭМГ свободы и тем больше выражен тренд. Чем ближе к 1,5, тем более зашумлен ряд, тем менее выражен его тренд, тем более лЭМГ случайна и склонна к неожиданным всплескам или угасанию активности.

• 2.    Антиперсистентная (эргодическая) иЭМГ (D = 1,5–2). Если такая иЭМГ демонстрирует «рост» в предыдущий период, то, скорее всего, в следующем периоде начнется спад. И наоборот, если шло снижение, то вероятен близкий подъем. Устойчивость такого анти-персистентного поведения зависит от того, насколько фрактальность близка к 2.

• 3.    Случайная иЭМГ (D ≈ 1,5) указывает на случайный ряд. События случайны и некорре-лированы. События в настоящем не влияют на будущий сигнал.

Сложные биологические процессы относятся к мультифракталам, то есть фрактальность временного ряда меняется в некоторых пределах. Поэтому при исследовании мультифракталов говорят об обобщенной фрактальной размерности [1], [7].

Статистический анализ производился в программной среде SPSS 14,0™. Корреляционный анализ производили с помощью непараметрического критерия Спирмена, сравнение средних значений – с помощью t теста Стьюдента.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Минимальный возраст, при котором получены записи иЭМГ, составил 32 мин после рождения. Пример записи этого ребенка представлен на рис. 1.

m. biceps br.

100    200   300   400   500   600   700   800   900   100

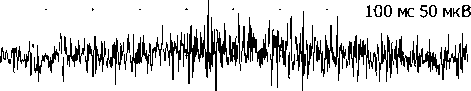
Средняя амплитуда

62,1 мкВ

D         D c        K 2

1,13 ± 0,17 4,435      10,66

m. triceps br.

100   200   300   400   500   600   700   800   900   100

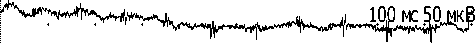
Средняя амплитуда < 10 мкВ

D         D c      K 2

1,08 ± 0,16 4,302   3,64

Рис. 1. Пример записи иЭМГ у ребенка в возрасте 32 мин после рождения

Корреляционная размерность в мышцах верхних и нижних конечностей ребенка в разных диапазонах амплитуды интерференционной ЭМГ

Мышца	Диапазоны амплитуды иЭМГ
	1–25 мкВ	25–50 мкВ	50–75 мкВ	75–100 мкВ
Корреляционная размерность (D c )
m. biceps br.	3,98 ± 0,61*	4,08 ± 0,61	4,19 ± 0,62	4,21 ± 0,96*
m. triceps br.	4,04 ± 0,53	4,00 ± 0,68	4,08 ± 0,65	4,07 ± 0,70
m. tibialis ant.	3,86 ± 0,60*	4,26 ± 0,57	4,28 ± 0,66	4,17 ± 0,51*
m. gastrocnemius	4,27 ± 0,58	4,41 ± 0,61	4,40 ± 0,70	4,96 ± 0,63
Корреляционная энтропия (К 2 )
m. biceps br.	3,09 ± 0,71	3,24 ± 0,78	3,39 ± 0,68	3,56 ± 0,71
m. triceps br.	3,29 ± 0,91	3,36 ± 0,85	3,47 ± 1,03	3,312 ± 0,52
m. tibialis ant.	2,91 ± 0,50	3,10 ± 0,65	3,41 ± 0,82	3,39 ± 0,54
m. gastrocnemius	3,25 ± 0,59	3,25 ± 0,55	3,63 ± 0,77	3,60 ± 0,43
Фрактальная размерность (D)
		1,4084 ±	1,4134 ±
m. biceps br.	1,35 ± 0,10	0,11	0,12	1,4866 ± 0,10
		1,4145 ±	1,4260 ±
m. triceps br.	1,37 ± 0,11	0,11	0,12	1,5065 ± 0,09
	1,3302 ±	1,4132 ±	1,4849 ±
m. tibialis ant.				1,4434 ± 0,14
	0,12	0,11	0,13
	1,3837 ±	1,4114 ±	1,4273 ±
m. gastrocnemius	0,13	0,15	0,12	1,4881 ± 0,12

* p < 0.001 при сравнении мышцы-флексора и мышцы-экстензора в паре антагонистов.

Установлено, что для всех исследованных мышц новорожденного корреляционная размерность D c составила ≈ 4,0, хотя выявлена недостоверная тенденция к росту для значений D c при увеличении амплитуды иЭМГ от 1–25 до 75–100 мкВ (см. таблицу). С точки зрения нелинейной динамики корреляционная размерность D c иЭМГ отражает количество уровней управления мио-электрическим сигналом и представляет собой количество уравнений, с помощью которых можно описать установившееся движение динамической системы, то есть иЭМГ и, соответственно, мышечного тонуса. Обращает внимание, что D c при амплитуде 25–75 мкВ почти одинакова, что, возможно, говорит об оптимальности генерации мышечного тонуса именно при данной амплитуде. Значения D c в мышцах-флексорах были на 0,2–0,4 меньше по сравнению с мышцами-экстензорами, что свидетельствует о бóльшей сложности сигнала иЭМГ в экстензорах.

Корреляционная энтропия иЭМГ К2 ребенка первых суток после рождения составляет ≈ 3.0 (см. таблицу). Согласно теории нелинейной динамики, бесконечное увеличение корреляционной энтропии говорило бы о полной непредсказуемости системы или ее неуправляемости и дезадаптации к данным условиям среды. В нашем же случае довольно низкая корреляционная энтропия иЭМГ новорожденного ребенка предполагает уже достаточно сформировавшийся к рождению контроль над мышечной активностью. Обращает на себя внимание различие значений корреляционной эн- тропии пар мышц-антагонистов. Например, значения К2 иЭМГ для мышц-флексоров примерно на 0,2–0,3 меньше по сравнению с экстензорами в каждом диапазоне амплитуды иЭМГ. Это указывает на бóльшую управляемость мышц-флексоров и бóльший, хотя и детерминированный, хаос в управлении экстензорами.

Также представляется интересным то, что при увеличении амплитуды иЭМГ происходит заметное, хотя и недостоверное, увеличение корреляционной энтропии. Это, в свою очередь, может говорить об увеличении пропорции хаоса (неуправляемости) при приближении к максимальным амплитудам иЭМГ. Подобное явление роста непредсказуемости иЭМГ было замечено ранее при исследовании больных паркинсонизмом [11], [13].

Фрактальная размерность иЭМГ ребенка D колебалась между 1,34 и 1,5, то есть соответствовала персистентным и/или случайным временным рядам (см. таблицу). Обращает на себя внимание рост фрактальной размерности в зависимости от амплитуды фрагмента, характерный и для других нелинейных параметров, что говорит об увеличении количества независимых аттракторов, определяющих иЭМГ. Также установлено, что фрактальная размерность не зависит от функции мышцы (флексор или экстензор), что отражает примерно одинаковую предсказуемость их иЭМГ. Возможно, это свидетельствует о едином центральном механизме управления этих разных по функции групп мышц.

Чем меньше фрактальная размерность процесса, тем больше выражен тренд и, соответственно, тем больше проявлено «целеполагание», то есть некое программирование этого процесса. В случае с иЭМГ, которую мы относим к персистентным временным рядам, низкие значения D означают высокую вероятность целеполагания. Особенно это характерно для иЭМГ с низкими амплитудами, которые можно отождествить с мышечным тонусом. Естественно, у новорожденного ребенка нет истинного осознанного целеполагания в движении, но имеются двигательные «программы», которые имеют свои определенные цели. Например, это программа формирования «эмбриональной» флексорной позы у ребенка, которая направлена на консервацию тепла. Подобная программа хорошо документирована для животных [4] и в меньшей степени проявляется у взрослого человека [5].

Следует отметить, что в первые часы после рождения ребенок находится в состоянии родового катарсиса, и флексорный мышечный тонус может быть выражен слабо (полуфлексорная поза) [8].

С другой стороны, установлено, что чем выше амплитуда иЭМГ, тем больше фрактальная размерность аттрактора, что говорит об увеличении количества нервных элементов (нейронов, центров, уровней), вовлеченных в управление, и тем больше при этом выражена случайность на иЭМГ. Действительно, иЭМГ с высокой амплитудой визуально выглядела как «вспышкообраз- ная», менее стабильная. Возможно, что спонтанная активность в виде вспышек на иЭМГ свидетельствует о вовлечении нескольких аттракторов (нервных центров), которые «конкурируют» между собой за «конечный общий путь». В совокупности с ростом Dc и K2 увеличение значений D свидетельствует о повышении сложности, хаотичности и непредсказуемости иЭМГ при увеличении амплитуды от 1 до 100 мкВ.

Нами исследована динамика нелинейных параметров в течение первых суток жизни по часам. Обнаружена достоверная положительная корреляция фрактальной размерности c часами жизни в течение первых суток после рождения для трех мышц , кроме икроножной, во всех амплитудных диапазонах (рис. 2). Из этого следует, что в течение первых суток жизни иЭМГ стремится от персистентных временных рядов к случайным. Вероятно, это отражает начальный этап «освобождения» двигательной системы от «эмбриональной» позы, характерной для внутриутробной иммерсии, и постепенный переход к антигравитационной активности. Достоверной корреляции других нелинейных параметров ( D c , К 2 ) с часами постнатальной жизни не выявлено, что говорит об их стабильности в течение первых суток жизни. Поскольку эти параметры отражают количество уровней управления и «долю» хаоса в управлении, можно предположить, что доношенный новорожденный ребенок уже оптимально готов к антигравитационной активности, хотя и не проявляет ее.

Большой интерес представляет динамика нелинейных параметров иЭМГ разных по функции мышц (верхние/нижние конечности, флексоры/ экстензоры). Установлено, что наиболее тесная и достоверная корреляция, например, фрактальной размерности со временем жизни была характерна для мышц верхних конечностей. Это, вероятно, отражает наличие кранио-каудального градиента в развитии двигательной системы. Обнаружено некоторое сходство в динамике нелинейных параметров между мышцами-флексорами верхних и нижних конечностей (двуглавая мышца плеча и передняя большеберцовая мышца).

Совершенно особое поведение демонстрируют нелинейные параметры икроножной мышцы. В частности, обнаружено полное отсутствие корреляции нелинейных параметров и даже фрактальной размерности со временем жизни. В определенном смысле, икроножная мышца «не реагирует» на изменившиеся условия существования (гравитация, снижение температуры) в течение первых суток. На наш взгляд, икроножная мышца, которая является классическим примером антигравитационной мышцы, сразу после рождения пока не вовлечена в антигравитационную активность. В то же время известно, что существует врожденный рефлекс опоры при прикосновении к стопам [8]. Таким образом, икроножная мышца будет проявлять свою врожденную рефлекторную антигравитационную ак- тивность только после гравитационной «сенсорной атаки». Первая собственная антигравитационная реакция возникает у ребенка только к окончанию первого месяца (удержание головки). Икроножная же мышца будет вовлечена в истинную антигравитационную активность только к окончанию первого года жизни в акте стояния.

ЗАКЛЮЧЕНИЕ

Нелинейные параметры представляют определенный интерес для оценки внутренней структуры иЭМГ, по скольку они чувствительны к уровню активности (амплитуде иЭМГ), ко времени жизни даже в течение первых суток жизни, а также к функции мышцы. Мы считаем, что нелинейные параметры могут быть полезным инструментом для исследования динамики антигравитационной активности у ребенка. Это может послужить полезной моделью для гравитационной физиологии. Для этого необходимо исследовать более поздние этапы неонатального периода и грудного возраста ребенка.

m. biceps br. (R = 0.07, p = 0,410)

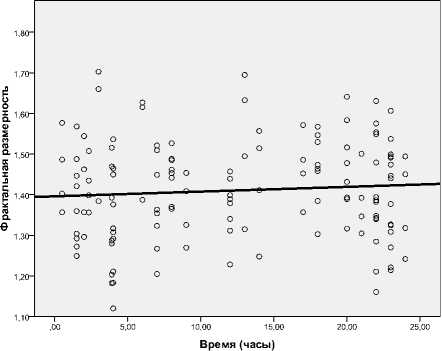
m. triceps br . (R = 0,195, p = 0,037)

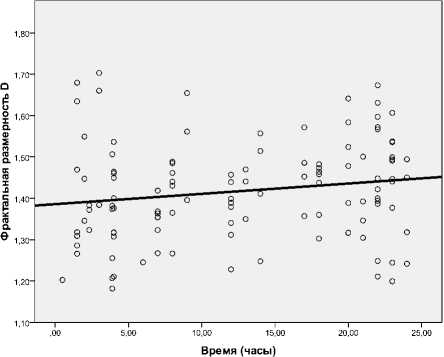
m. tibialis ant. (R = 0,036, p = 0,695)

m. gastrocnemius (R = -0,108, p = 0,257)

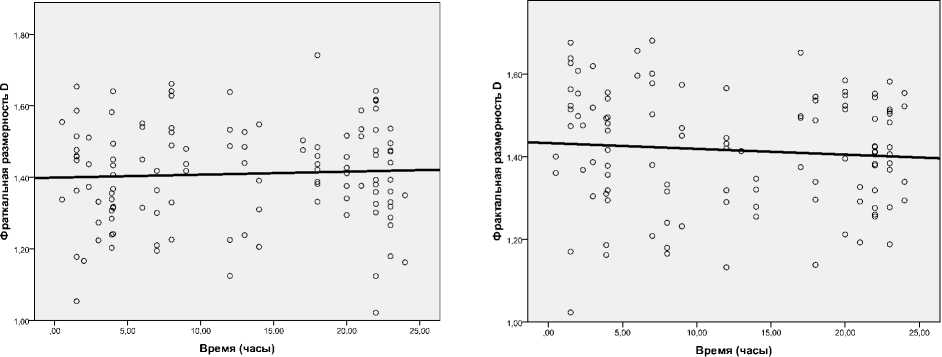
Рис. 2. Динамика фрактальной размерности иЭМГ в течение первых 24 часов жизни для мышц-антагонистов верхних и нижних конечностей