Динамика несолитонных импульсов в нелинейном информационном канале

ДИНАМИКА НЕСОЛИТОННЫХ ИМПУЛЬСОВ В НЕЛИНЕЙНОМ ИНФОРМАЦИОННОМ КАНАЛЕ

Одно из применений ультракоротких световых импульсов связано с перспективами передачи больших объемов информации по оптическим волокнам. Короткая пространственная протяженность таких импульсов ^1 мм способствует их дисперсионному расплыванию и ухудшению скважности при распространении по световоду. Стабилизация таких импульсов может быть связана с конкуренцией нелинейных и дисперсионных эффектов. При этом для работы волоконно-оптических линий связи требуется специальный набор сигналов, играющих роль элементарных символов. Первые проекты таких линий были связаны с солитонами [1], огибающие которых не содержат свободных параметров. Однако на расстояниях, ограниченных несколькими дисперсионными длинами, что характерно для вычислительных комплексов, передача несолитонных сигналов, устойчивых на этих расстояниях, позволит использовать для кодирования сообщений свободные параметры таких сигналов. Указанная возможность представляет интерес для передачи сигналов многозначной логики и использования кодов более сложных, чем традиционный двоичный код.

Эволюция нормированной комплексной огибающей ф(т, п) = Е(п, т)Е(0, т)-1 интенсивного короткого импульса в одномодовом оптическом волокне с квадратической зависимостью показателя преломления от амплитуды поля n=nQ+n2|Е|2 и пренебрежимо малым затуханием в области аномальной дисперсии описывается, как известно, нелинейным уравнением Шредингера

1 2i + 5—^ + н | ф I 2ф=0

Зп эта

с начальным условием ф (0, т)=Фо(т), определяемым импульсом на входе волокна, где пит- нормированные координаты, связанные с продольной пространственной координатой z и реальным временем t соотношениями в которых vq - групповая скорость, L^, Tq - характерные масштабы, а и =L а)с**1п |Е|2  - параметр нелинейности, определяемый как свойствами материала со 2 о щ самого волокна, так и входным импульсом,

В уравнении (1) пренебрегается дисперсией выше второго порядка, зависимостью групповой скорости от интенсивности и затуханием.

Хорошо известно стационарное решение нелинейного уравнения Шредингера (НУШ) (1) в виде солитона огибающей

IФ (и г т)I2=ch~2(V^ т).(2)

В отличие от (2), здесь рассмотрены параболические финитные импульсы ф (т) = Ь1^2)2 ? т251'*(3)

[  0;т=>1;

безразмерная энергия которых W:

W = Лф (T)|2dT = ^^t1) ;

-1  °           r(v+f)

где Г - гамма-Функция зависит от параметра v. Рисунки 1 и 2 иллюстрируют темп эволюции огибающих с крутым (v<2) и сглаженным (v>2) фронтом.

На рис. 1а, б показаны зависимости максимума интенсивности импульса и его полуширины на уровне максимума интенсивности Н от переменной т) при v=2 для нескольких значений и» Тенденции изменения параметра Н противоположны тенденциям эволюции максимума интенсивности 1Ф1^« Для сравнения здесь же приведены зависимости, соответствующие линейной эволюции (х=0).

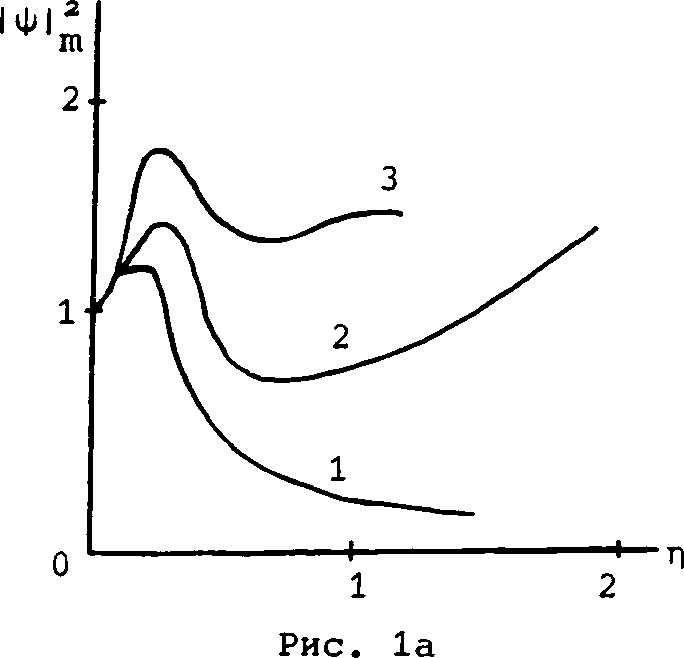
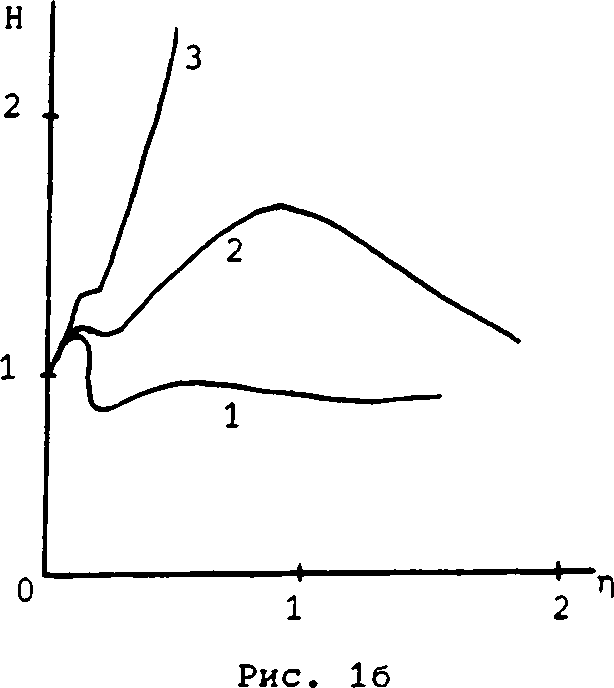
Рис. 1. Эволюция параболического импульса (3) при v=2; кривые 1, 2 и 3 соответствуют случаям х=0; х=2,5 хк₽ и и=4 икр. Показаны динамика максимума интенсивности

|ф|^ и ширины импульса на уровне 0,5|ф|2

н

1,5

-----1------1-------------1--------------1--------------«-----------n 0,2     0,4    0,60,8

Рис. 2a

--------------1--------------1--------------1---------------1^

0    0,2   0,4   0,60,8

Рис. 26

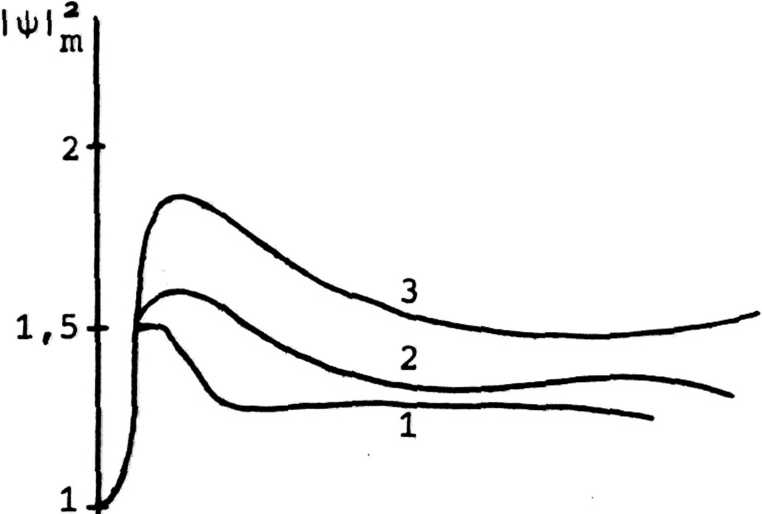
Рис. 2о Влияние периферии импульса (3) на эволюцию огибающей интенсивности при и=4 xKp(v); кривые 1, 2 и 3 соответствуют значениям v=5; 3 и 1О Показаны динамика максимума интенсивности 1Ф1^ и ширина импульса Н на уровне 0,5

Из графиков видно, что с увеличением параметра и колебательная эволюция сменяется монотонной в случае иМи пГ3 (^)

Мкр ra(v+2} при этом импульс на расстояниях п£1 принимает почти стационарную форму. Дальнейшее увеличение м вновь усиливает колебательные тенденции в динамике импульса.

Таким образом, область значений параметра эволюции и вблизи и=4и ^ соответству-кр ет замедлению темпа перестройки импульса. Рис. 2а, б иллюстрирует монотонную эволюцию при и=4к (v) различных огибающих семейства (2), кр

Одной из важнейших задач при построении системы связи является оценка мак симально допустимой скорости передачи информации. С этой целью было исследовано взаимодействие двух импульсов в процессе их распространения по одномодовому волокну и находилось максимальное расстояние, которое проходили по волноводу импульсы, оставаясь различными между собой. Различимость понималась в смысле Рэлея, т.е. импульсы считались различимыми, если интенсивность поля между ними была меньше половины максимумом интенсивности импульсов.

Начальное условие в НУШ (1) взято в виде

Фо (т )=ФО (т-Д т )+Фо (т+Дт);

где Дт - половина расстояния между центрами импульсов, Рассматривались два типа огибающих: гауссовская f (т)=ехр(- 2- ) и секанс-гиперболическая ф (т^сЬ-1^ т)

2т’                                  °            2

причем масштабный множитель т^ гауссовского импульса выбирался так, чтобы уравнять И обеих импульсов в начале эволюции.

результаты эволюции даны на рис. 3, где для фиксированных длин линии связи показаны зависимости от ширины импульса t_q минимально допустимого сближения импульсов ^T_min при передаче, обеспечивающего различимость импульсов при приеме. Максимально достижимая скорость передачи “(Дт . )~¹.

min

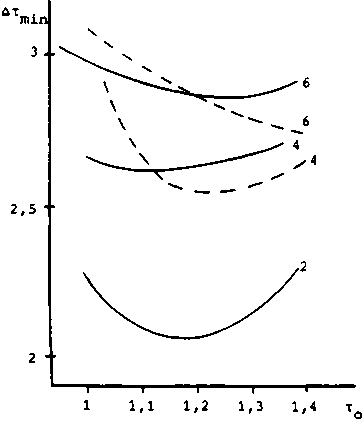
Рис. 3. Зависимость минимального допустимого интервала между импульсами Дтт^п от их начальной длительности то, при котором импульсы остаются различимыми в смысле критерия Рэлея при распространении на расстояние п, отмеченное на кривых (х=2)

Из рис. 3 видно, что каждой длине линии связи соответствует своя оптимальная ширина то импульса данной огибающей, причем максимально достижимая скорость передачи импульсами гауссовской формы с учетом выбора то может быть больше, чем для импульсов секанс-гиперболиче-ской формы.

Рис. 3 характеризует взаимодействие импульсов до тех пор, пока максимальное значение интенсивности в области перекрытия удовлетворяет критерию Рэлея. Дальнейшая эволюция может привести к периодическим режимам слияния и расслоения импульсов. Такой режим для солитонов был известен ранее [з]. Та же тенденция прослеживается при эволюции параболических импульсов (3) при том же начальном расстоянии т=4.