Динамика нестационарных систем с равномерно изменяющимися во времени коэффициентами

Для моделирования динамики нестационарных систем автоматического управления достаточно широко применяются линейные дифференциальные уравнения с переменными коэффициентами. Рассматриваются методы получения аналитических зависимостей между параметрами переходных процессов и параметрами системы управления, основанные на применении преобразования Лапласа к линейным системам обыкновенных дифференциальных уравнений с линейно изменяющимися во времени коэффициентами.

ПОСТАНОВКА ЗАДАЧИ

Наибольшее распространение линейные системы обыкновенных дифференциальных уравнений с линейно изменяющимися во времени коэффициентами получили при моделировании динамики нестационарных систем управления (НСУ) высокоскоростными динамическими объектами, называемых "нестационарными системами управления с особой точкой" [1] или "системами управления конечным положением" [2].

Математический аппарат, пригодный для анализа и синтеза НСУ, основан на использовании результатов, полученных еще в конце 18 века П. Лапласом. Он был опубликован в 1957-1958 гг. немецкими математиками Г. Людвигом и Х. Роллни-ком [1, 2] и получил дальнейшее развитие в работах профессора А.Т. Барабанова [3, 4]. Однако в этих работах отсутствуют методы получения аналитических зависимостей фазовых координат динамического объекта от параметров НСУ на всем интервале интегрирования.

Для математического описания НСУ можно воспользоваться системой линейных дифференциальных уравнений в форме [3]

Q 11 ⁽ Р ) x 1 + Q 12 ⁽ Р ) x 2 + ^ + Q 1 n ⁽ P ) x n =

= L 1 ⁽ P ) ~ + f l ⁽ t X τ

Q 21 ( P ) x 1 + Q 22 ( P ) x 2 + ^ + Q 2 n ( P ) X n =

= L 2 ( p ) -¹ + f ₂( t ),                         (1)

τ где p =--обозначение производной по време-dt ни; т = t -t0, 0 < t < t0, t0 — длительность переходного процесса; Qj (p), Li (p) — линейные дифференциальные операторы с постоянными коэффициентами, i = 1, 2,..., n, j = 1, 2,..., n.

В работе [3] решение системы дифференциальных уравнений (1) при нулевых начальных условиях сведено к интегральному представлению вида c+i∞

X j (t ) = .   f W j < Р ) F ^ ( Р ) ' +

2ni J c-i∞

1 p

+ Wa1(P)Fa (P)ePt0 ~— J e^u j (z)dz}dP, ^(P) t j = 2,..., n;

c+i∞ x 1(t) =      J {Wa1(P)Fa (P)ePt0 X

2ni J c-i∞

1P x—- fezT^(z)dz}dp, ^( P) t где Waj(p), j =1, 2, „., n — передаточная функция контура НСУ с разорванной нестационарной связью от входа по воздействию c+i∞ fa (t) = — \ptFF. (p)dp

2ni J c-i∞ до выхода звена с коор-

динатой Xj (t); Fa (p) — преобразование Лапласа от функции      fa (t);      Uj (z) = ^( z) Rj( z);

Q n 1 ⁽ P ) x 1 ⁺ Q n 2 ⁽ P ) x 2 ⁺ - ⁺ Q nn ⁽ P ) x n =

= L n ( P ) ^{x 1} + f n ( t ), τ

n

^ L i ( z ) A j ( z )

R.(z) = -i=1------------; Xi (t) — первая (опреде- j           A(z)

ляющая) координата НСУ; Rj(z) — сумма переда- точных функций контура управления от входов е Х1 (t)

по воздействию q = —— до выхода звена с коор-τ динатой Xj (t)

Функция ф(p) может быть найдена как решение дифференциального уравнения dyp- = -Ф( p) ■ ф( p), dp где

n

^{ф (} p ) = 2 L j ⁽ p ^{) W}j i ⁽ p );

j = 1

A- ( p ) w j ( p ) = J ; ^{a (} p )

A ( p ) =

Q 11 ⁽ p )

Q ₂₁( p )

Q 12 ⁽ p )  -   Q 1 n ⁽ p )

Q 22 ⁽ p )   ^-   Q 2 n ⁽ p )

Q n i ( p )

^Qn 2 ⁽ p )  - ^Qnn ⁽ p )

;

A j ( p ) — алгебраическое дополнение элемента Q j ( p ) определителя A ( p ); Ф ( p ) — передаточная функция от выхода нестационарного звена — до τ выхода по координате z . Передаточная функция Ф ( p ) называется определяющей передаточной функцией.

В случае, когда различны все корни характеристического уравнения A ( p ) = 0 и функция Ф ( p ) является дробно-рациональной, _{m                       m}          - α _k

Ф(p) = 2--k— и ^(p) = П (p - zk )  , k=1 p - zk            k=1

где z k — корни характеристического уравнения A ( p ) = 0, ( k = 1,..., m ); a ^ — коэффициенты разложения на простейшие дроби функции Ф ( p ).

Таким образом, решение задачи Коши в работе [3] сведено к вычислению интегралов (2). Основную трудность при аналитическом вычислении переходных процессов по формулам (2) представляют интегралы типа c+i∞

J ( t ) = — J{ e pt ⁰ X 1 ( p ) х

2ni c-i∞

p х — |>р(z) • X2(z) • dz} • dp, ^(p) £

где X 1 ( p ), X ₂( z ) — дробно-рациональные функции своего аргумента.

Обобщая результаты работ [1-4, 6], изложим об- щую схему вычисления интегралов типа (3), пригодную для вычисления переходных процессов на всем интервале интегрирования системы уравнений (1).

Метод вычисления интегралов (3) для дробнорациональных и имеющих только простые полюсы функций X 1 ( p ) и X ₂ ( z ) заключается в замене пути интегрирования вдоль мнимой оси ( с = 0) на путь интегрирования по замкнутому контуру в предположении, что т >  0 (рис. 1). Этот контур включает мнимую ось и полуокружность бесконечно большого радиуса в левой полуплоскости (полуокружность на рис. 1 не показана), описанную против часовой стрелки (в положительном

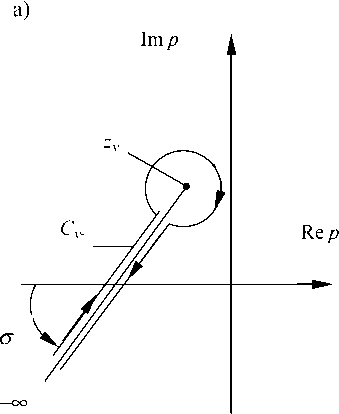
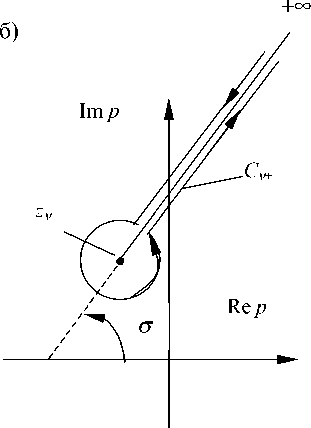
Рис. 1. Контуры интегрирования в комплексной плоскости. Пояснения в тексте

направлении) с обходом всех особых точек подынтегрального выражения по петлям C _v - (рис. 1, а), каждая их которых из бесконечности идет вдоль луча ( -те , z k ) под углом а и, возвращаясь в ( -те ), по часовой стрелке охватывает только одну особую точку выражения

1 р

----- e^{z т} ф ( z ) • X ₂( z ) • d z . Интеграл по такому ф ⁽ Р ) 1

контуру будет равен интегралу вдоль мнимой оси и сумме интегралов по петлям Cv -, т. к. интегра лы по дугам окружности бесконечно большого радиуса равны нулю. С другой стороны, этот интеграл будет равен сумме вычетов в полюсах функции X 1 (p), не совпадающих с особыми точками

1 р функции ---- ezтф(z) • X2 (z) • dz . Соотношения

ф ⁽ Р ) *

между интегралами по различным участкам контура интегрирования можно условно изобразить в виде следующей схемы выполнения операций:

внешнего и внутреннего интегралов, взятых вдоль луча (-те,zv), и интеграла по окружности беско- нечно малого радиуса с центром в точке zv

z v : J — = J e pt ⁰ -J

C v     -те

-те

e^zz — +    J — . При обходе

=             I Р - zv - const\ ₊

контура интегрирования Cv эта окружность обходится по часовой стрелке. Поскольку вычисление интеграла по окружности далее сводится к вычислению вычета [7], направление обхода окружности изменим на обратное и соответственно изменим знак перед интегралом по окружности. Внешний и внутренний интегралы в формуле (3) могут быть представлены интегралами по петлям, исходящим из бесконечности в левой полуплоскости и обходящим точку zv по часовой стрелке с изменением аргумента в пределах (0,-2п ), если пара- метр экспоненты во внешнем и во внутреннем интегралах принимает положительные значения.

В нашем случае 1 ₀ > 0, поэтому для внешнего интеграла можно принять [6]

с + i ^те       m

J-+X (—1 —)

с - i те      ^{v - 1}       C v

v - m + q

- X Res— v - m+1 p zv

zv

J e pt ⁰

-те

e ^а i -1 _г C _v

J e pt ⁰ —

или c+iте

J — c - iте

m              v = m + q

-X(- J-) + X Re5—} v-1 Cv       v - m+1 p - zv

v=m+q где X Re 5{"} v=m +1 p = zv

сумма вычетов в полюсах

функции X ₁ ( p ) , не совпадающих с особыми точ-

Для внутреннего интеграла т - 1 - 1 0 <  0 , поэтому необходимо сформировать аналитическое продолжение внутреннего интеграла в область отрицательных значений т . Решением этой задачи будет выбор контура интегрирования внутреннего интеграла в виде петли в правой полуплоскости C _{v +} (рис. 1, б). Такая замена может быть представлена схемой

1 ками функции ---- ф ⁽ Р )

p

J e^{z т} ф ( z ) • X 2 ( z ) • d z ; J — —

-те

C v

интеграл по петле, которая охватывает по часовой стрелке (в отрицательном направлении) только

J ez

-те

т > 0

^

_e-^сц, • i - 1

J

Cv +

т < 0

одну 1

ф ⁽ Р )

особую

p

J e^{z т} ф ( z ) • X 2 ( z ) • d z .

-те

точку

выражения

Далее J — вычисляется как сумма произведения C v

Легко видеть, что правые части формул (5) и (6) отличаются не только изменением направления интегрирования, но и соответствующим изменением знака перед дробями. Поэтому в соответствии со схемой (4) в качестве исходного примем следующее представление интеграла (3)

m

J ( t )  -- У----- ;—г [ e pt ⁰ X, ( p )

2ra'X1 - eа J

Cv -

1 ф ⁽ p )

d p х J e^{z т} ф ( z ) X ₂( z )d z

Cv +

+

m

+ — X e z ^vT 2ni t-i

х     J e^{pt 0} X 1 ( p )

I p - zv - const 1 +

Ф v ( Р )

( Р - z v ) - ^{Pv + 1} S 3 v ( Р )d p +

+

X Re s - v - m + 1 ^{p - p} v

e^{p 0} X 1 ( Р )

1 ф ( Р )

p те e^(z) X2(z)dz

где C V ₊ — петля в положительном направлении (рис. 1, б), C _v - — петля в отрицательном направлении (рис.1, а); | р - z _v\ = const ₊ — замкнутый контур интегрирования, охватывающий только одну особую точку z = z _v в положительном направлении; p _v — порядок полюса функции X ₂ ( z ); q — число полюсов функции X 1 ( р ), не совпадающих с особыми точками функции ф ( z ) X ₂( z ); ст = 0 в том случае, если все мнимые части особых точек различны;

Для решения поставленной задачи, обобщая результаты работ [1-4], изложим методы вычисления всех интегралов, входящих в структуру (7) интеграла (3).

ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ—КОНСТАНТ

Рассмотрим интеграл

J 1 v ( t о ) = ( e ⁰ X 1 ( Р )-1-d Р , /          Ф ( Р )

CV —

i

53v (р) = ^ D3v к к=0

^{( Т} )

⁽ Р ^— z v ) k

— av — Pv + к + 1

D 3 v к ^{( т} ) = ₁ . к !

\к                   "

^{+ Т}  Ф v ⁽ Р ) X 2 v ⁽ Р )

- Р = zv

.

Интегралы по окружностям | р — z _v | = const учтены в формуле (7) на случай, если X ₂( z ) имеет кратные полюсы ( p_v = 2, 3, „.) и/или функция X ₁ ( Р ) имеет полюсы, совпадающие с особыми точками функции ф ( z ) X ₂ ( z ). Для вычисления составляющих, соответствующих полюсам ( p = р_к ) функции X ₁ ( Р ) , не совпадающим с особыми точками ( z = z _v ) функции ф ( z ) X ₂( z ), используются теорема Коши о вычетах и разложение в ряды

где        ф ⁽ р ) = ⁽ р ^{— z} _v ) ^а • Ф v ⁽ р );        X 1 ⁽ р ) =

= ( Р — z v ) ^{— Pv} • X 1 V ( Р ); a_v — нецелое число; p _v — целое число, порядок полюса функции X 1 ( р ) в точке р = z _v ; X_{1 v} (р) — дробно-рациональная функция, не имеющая полюса и нуля в точке Р = z v .

Разлагая в ряд по степеням ( р — z _v ) функцию D 1 v ⁽ Р ) = X 1 v ⁽ Р )—*    , получим

Ф v ⁽ Р )

i

J 1 V ( t о ) = 2    D V ) ( z v ) J 1 V, ( t о ),        (9)

t= *0 ^ ^!

где

1 Р к

Тейлора функции ------ е^{2 Т} ф (z ) X ₂( z )d z .

Ф ⁽Р к ) i

В структуру выражения, определяющего значение интеграла (7), входят интегралы-константы и интегралы-функции времени, оставшегося до конечной текущей точки (КТТ) ( — Т = t о — t ).

С .             « V — P v + e

J 1 v _M ⁽ t g ) = J е^{Р 0 (} Р ^— z v )        ^d Р ,

Cv —

D 1 ⁽ v ⁰⁾( z v ) = X 1 V ( z v )^-, Ф v ⁽ z v )

^

D ( ^ ) _{( z} ) = _d_

^{1 V V}     d z e

Методы решения задачи Коши, изложенные в работах [1-4], не получили такого широкого распространения, как методы операционного исчисления [7], поскольку, в частности, к настоящему времени недостаточно проработаны методы вычисления интегралов-функций времени, входящих в формулы (3), что не позволяет установить зависимость параметров переходных процессов от параметров НСУ.

В настоящей работе ставится задача разработки методов получения аналитических зависимостей

v I

X 1 v(zv)

Ф v ^{( z} v ) v

.

После замены переменной р — z _v = и интеграл J \v_e ( t ₀) преобразуется к виду

параметров переходных процессов от параметров НСУ не только в КТТ, но и на всем интервале интегрирования системы уравнений (1). Это позволит оптимизировать параметры всей траектории, а не только конечного положения нестационарного динамического объекта.

а — p + e

J 1 ve ( t о ) = e^{z v t 0} J e ⁰ и         d и .

C 0 —

Выполним замену переменной и = — — . Если t ₀

аргумент переменой и изменялся от 0 до 2 п , то аргумент у будет изменяться в пределах (- п , + п ), что соответствует контуру интегрирования, подобному C _{0 +} , но при обходе его в обратном направлении. Изменяя направление обхода контура, получим

Jw^ ( 1 0 ) = - e^{Z v} ‘ ⁰

-av + Pv -ц-1 П(av -Pv + ц+1)i t0           e

×

-   αν - ρν + µ x I e p p        dp.

c 0 +

G 1 v^ ^{( z} v )

D v ) ( Z v )

D 1 ⁽ v ⁰⁾( Z v ) "

В случае, когда все мнимые части особых точек подынтегральных функций различны, петлеобразные контуры интегрирования J ... в формулах

C ν

типа (8) можно провести вдоль лучей, исходящих из особых точек и параллельных действительной оси. Тогда интеграл в формуле (10) с точностью до

постоянного множителя совпадет с представлением Ханкеля гамма-функции в виде интеграла по контуру [6]

Полученный ряд 5 _{1 v} ( 1 ₀) является асимптотическим по t ₀ рядом, пригодным для вычисления интеграла J _{1 v} ( t ₀) при больших 1 ₀. Для практического использования асимптотический ряд 5 _{1 v} ( 1 ₀) с определенными числовыми коэффициентами может быть просуммирован каким-либо из известных методов суммирования асимптотических рядов [8].

Г ( а ) = - — ---- f ( - p ) ^{a - 1} e " ^p d p .

2 • i • sin na /

^C 0 +

Следовательно,        подставляя для z = av - pv + ц + 1 выражение

J p^{z - 1} e ^{- p} d p = e ^{- n} " ^{Z - 1) i} • J ( - p ) ^{Z - 1} e ^{- p} d p =

^C 0 +                              ^C 0 +

= - e^-n'^zi • ( e^-n'^zi - eⁿ'^zi ) • Г ( z )

в формулу (8), получаем

J v ⁽ t 0 ) =

M 0 /^{- a} v ⁺ P v ^- ц ^-1 _on ( a v -P v + ц + 1) i f - pp „ “ - ^{Pv + Ц}

- e  t ₀       e          ep

^C 0 +

d p =

= e^{z v 0} t -

■ a ^{+ p} v ^- Ц ^{- 1} ( e ^{- п} ( a ^{- p} v ⁺ Ц + 1) i

-

e n ( a v -P v + Ц + 1) i ) x

xr ( a v

^{- p} v ^{+ Ц + 1)}

- 2 пц i .

и, поскольку e = 1, а

πµ i        µ e   = (-1)ц, то в соот-

ветствии с формулой (9) получаем

J 1 v ( 1 0 ) = - 2 ie^{Z vt 0} t + ^{P 1} sin n ( « v - P v + 1) x

У У (7 Л Г( av - Pv + 1) о /. \ x X 1v (zv ) z X      5 1v (t 0),        ('ll)

P v ( Z v )                    ⁽¹¹⁾

где

∞

51v (10) = 2(-1)Ц ц=0

^{r ( a} v ^{- P} v ^{+ ц + 1)} _Г      .

и I G 1 v,u ^{( Z} v );

^{r ( a} v ^{- P} v ^{+ 1)} • t 0 • ^{ц !}

МЕТОДЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ — ФУНКЦИЙ ВРЕМЕНИ

Методы вычисления интегралов — функций времени вида

J 2v (t -10) = J ezz^( z) X 2( z )dz , (12) Cν+ входящих в структуру (7), известны для больших значений (-т), для которых удается построить эффективные асимптотические разложения, а также для малых значений (т* - т), где т* < 0 — малая величина [1, 2]. Однако выполненные нами расчеты переходных процессов по асимптотическим формулам, приведенным в [1, 2], оказались достаточно точными лишь на небольшом интервале интегрирования системы уравнений (1).

Поэтому для построения аналитических зависимостей, пригодных для оценки переходных процессов на большем интервале, в данной работе был использован другой подход — разложение интегралов (12) в ряды Маклорена по текущему времени t . При таком подходе коэффициентами степенного ряда оказываются интегралы, в подынтегральных выражениях которых остается множитель exp(- pt ₀), обеспечивающий сходимость интегралов при Re( p ) >  0. При этом условие сходимости выполняется именно на контурах, ветви которых уходят в правую полуплоскость комплексной переменной и по которым осуществляется интегрирование интегралов-функций времени.

Для получения расчетных формул преобразуем формулу (12) для интегралов — функций времени

^J2 v ⁽ t - t 0 ) = J ^{e P T} ^ ⁽ p ) ^X 2 ⁽ p ^)d p = J ^{e P T (} p - ^Z v ) + ^av • ^ v ⁽ p ) • ⁽ p - ^Z v ) ^{- в} • ^X2 v ⁽ p ^)d p = ^C ν +                      ^C ν +

= e^{Z vZ} J e^{p r} p ^{-av - Pv} • ф v ( p + Z v ) • X 2 v ( p + Z v )d p .                                                  (13)

С 0

В формуле (13) интегрирование проводится в комплексной плоскости по петле, обходящей начало координат против часовой стрелки и вытянутой вдоль луча, выходящего из начала координат в положительном направлении под таким углом, что путь интегрирования не проходит ни через одну из особых точек функции Ф v ⁽ Р ± z v ) ^- X 2 v ⁽ Р ± z v ).

Обозначим

J 0 v ^{( т} ) =

= J e ^{p T} Р "^ - ^{в -} Ф v ⁽ P ± z v ) ^- X 2 v ⁽ P ± z v ^)d P •   ⁽¹⁴⁾

C 0

Интеграл (14) является аналитической функцией времени t в промежутке (0 <  t <  t ₀ <  t ₀). Благодаря соответствующему выбору контура интегрирования подынтегральная функция в (14) является аналитической функцией, и интегралы

J 0 v k ^{( т )} =

k

= / —TeP(t—t0)Р^ —Pv - Фv (Р ± zv ) - X2v (Р ± zv )dР, C0 dt k = 1, 2, 3...

сходятся равномерно во всех точках промежутка 0 <  t <  t ₀. Следовательно, интеграл J _{0 v} ( т ) можно разложить в ряд Маклорена

^J 0 v ^{( т} ) = ^J 0 v 0 ^{( —} t 0 ) ± ^J 0 v 1 ^{( —} t 0 ) ^- t ±

, J 0 v 2 ⁽ t 0 )    ,2 .

+-- - t + ...,

2!

где

J 0 v k ^{( —} t 0 ) =

= J e ^{— pt 0} p k ^{a — в -} Ф v ⁽ Р ± z v ) ^- X 2 v ⁽ P ± z v ^)d P , C 0

k = 0, 1, 2, 3,...

Разлагая функцию ф_v ( p + z _v ) ^- X 2 v ⁽ P ± z v ) ^в ряд Маклорена по положительным степеням Р , получим

J 0 v k ( — 1 0 ) = J e - ^P t ⁰ P k ^a - ^в -S 2 v ( P )d P ,    (16)

C 0

где у ( X V D2vJ(zv) j

^S 2 v ⁽ P ) = L  ,--- P ^, j = 0     J!

d ^j

D 2 v J ⁽ z v ) = —" [ ф у ⁽ z v ) • X 2 v ⁽ z v ^{) ]} .

d z v

Следовательно, интеграл (15) может быть вычислен по формуле

J 0 v k ( — 1 0 ) = J e - ^P t ⁰ P k ^—av - ^ " -S 2 v ( P )d p =

C 0

= ( e -²"- ' — 1 ) $ 2 v k ( 1 0),               (I⁷)

где

$ 2 v k ⁽ t 0 ) =

^

= 2 ( — 1) ^J

J = 0

D 2 v j ⁽ z v ) ^{r ( k} + ^{J — a} v ^— P v ⁺ 1) j !             tk^+J—a v ^— P v ^{+ 1}

Для практического использования асимптотический ряд $_{2 v k} ( 1 ₀) может быть просуммирован каким-либо из известных методов суммирования асимптотических рядов [8]. С учетом (14)-(17) интеграл (13) может быть вычислен по формуле

J 2 v ( t — 1 0 ) = ( e "¹" ^a " ⁱ — 1 ) e ^z - ' V v ( Z v ) - X 2 v ( Z v ) -^Г^ О;- А т ^±1) B v ( t , 1 0 ),

X                                                              , ^av P v ±¹

t ₀

где B v ( t , 1 0 ) = 1 ± ^{( av в} ± ** G„ , ( 1 0 ) - 1- ± - _                  ^1!                              t 0

J = 1, 2, 3,_.

G 2 v k ( 1 0 ) = l ^ ^ k T t ⁰^ ;     $ 2 v 0 ( 1 0 ) = Ф v ( Z v ) - X 2 v ( Z v )1

$ 2 v 0 ⁽ t 0 )

Для практического использования асимптотический ряд B _v ( t , 1 ₀) может быть просуммирован каким-либо из известных методов [8]. Если ряды $ _{1 v} ( 1 ₀) и B _v ( t , 1 ₀) оказываются сходящимся, то, как показывает приводимый ниже пример, использование операции суммирования может привести к получению точного аналитического решения.

Возвращаясь к формуле (7), заметим, что все составляющие первой суммы при нецелых av уже могут быть вычислены: J — в соответствии с

Cv— формулой (11), J — в соответствии с формулой

Для целых av вычисление интеграла (13) не- обходимо производить обычным образом — с использованием теоремы Коши о вычетах:

J _{0 ν} ( τ ) = ∫ e^{p τ} p ^{- αν - βν} ⋅ ϕ_ν ( p + z _ν ) ⋅ X _{2 ν} ( p + z _ν )d p = C 0

= 2 π ⋅ i ⋅ Re s { e^{p τ} p ^{- αν - βν} ϕ_ν ( p + z _ν ) X _{2 ν} ( p + z _ν ) } . p = 0

В результате вычисления получится полином по τ степени ( α_ν + β_ν - 1) [6].

Формулы (11) и (18) были использованы для получения аналитических зависимостей параметров переходных процессов от параметров НСУ третьего порядка. Сравнение результатов расчетов по формулам и машинного решения соответствующей системы дифференциальных уравнений показало, что формулы (11) и (18) могут удовлетворительно моделировать переходные процессы практически на всем интервале времени переходного процесса, на котором принятая математическая модель адекватно отражает динамику НСУ.

Рассмотрим пример применения изложенных методов для получения аналитических зависимостей параметров траектории от коэффициентов модели, отражающей движение динамического объекта как материальной точки.

ПРИМЕР: ПЕРЕХОДНЫЙ ПРОЦЕСС, ВЫЗВАННЫЙ НАЧАЛЬНЫМ ОТКЛОНЕНИЕМ

ПЕРВОЙ КООРДИНАТЫ ОТ ЗАДАННОЙ ПРЯМОЛИНЕЙНОЙ ТРАЕКТОРИИ

Если заданная траектория — прямая линия, то начальное условие по первой координате определяется отклонением от этой траектории. Изменение первой координаты в отклонениях от прямой линии можно представить в виде

τ x1 =η- x1(0) ,                  (19)

t ₀

где η — отклонение первой координаты от требуемой прямой линии в переходном процессе; x ₁ (0) — начальное отклонение первой координаты от заданной прямой линии.

Рассмотрим движение относительно заданной прямолинейной траектории материальной точки с передаточной функцией Φ ( p ) = α ¹ (рис. 3). ^p

В этом случае ϕ( p ) = p -α1 . Для того чтобы воспользоваться формулами (2) в части, относящейся к координате x1 , необходимо заменить ее с помощью формулы (19) на координату с нулевым начальным значением. При этом очевидно, что на выходе нестационарного звена появится τ постоянное воздействие - x1 (0) , а к производ-t0

ной новой фазовой координаты η необходимо до бавить постоянное воздействие   x1 (0) . Обозна- t0

α              1

чим W11(p)= 1 ; W21(p)= ; F1(p) =- 1;

p               pt

F2 ( p ) = x1 ( ) . Полагая далее     Wσ 1 Fσ 1 = t0

=W11F11+W21F21 в формуле (2) для координаты x1 (t) , с учетом (19) получим x1(t)= τ c+i∞(1-α1) x1(0) 1 ept0pα1pezτz-α1dzdp-τ x1(0) = 2πi c-i∞    p      t0   p ∞t0

c+i∞

τ x1(0)1-α1     ept0pα1-2 ezτz-α1dzdp-τ x1(0) = t         2πit

0                 c-i∞            ∞ x1 (0) ⋅τ t0

⋅

2 π i

(1 - α ₁)

_{1 -} e - 2 πα ₁ i

∫ e^{pt 0} p ^{α 1 - 2}d p × ∫ e^{p τ} p ^{- α 1} d p +

C 1 -                      C 1 +

x (0) ⋅ τ 1 - α

+ ¹            ⋅          ¹

t ₀       2 π i

ept0p-2 ⋅ p⋅S3(p,τ)dp-x1(0)⋅τ , t p =const                                      0

∞ где S3(p,τ) = ∑ D31k(τ)

k = 0

pk

- α ₁ + k + 1

D ₃₁₀ ( τ )

1 - α ₁

+ D ₃₁₁( τ )   ^p + …

2 - α ₁

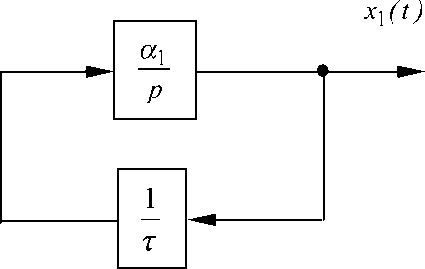
Рис. 3. Схема управления движением материальной точки по заданной прямолинейной траектории

= ( e "^2аа^ — 1) ^{Г (2 а} 1 ) • ( — т ) ^а 1 ^{— 1} , (1 — а 1 )

где

B 1 ( t ) =

( — а , + 1) t

= 1 + -—v---) • — +

L 1!          1 0

, ^{( — а} v ⁺ 1) • ^{( — а} v ^{+ 2)} 1 1 _t +----+ ..

2!                 t ₀ ²

7 _t

1—7

^V     t ⁰

а ₁ - 1

.

•

Вычислим коэффициент D _{31 к} ( т ) при к = 0:

В этом конкретном случае ряд B 1 ( t ) оказался суммируемым и сходящимся к степенной функции.

Объединим полученные результаты

D 310 ^{( т} ) = о!

. dp^+т

X ⁰

Ф v ⁽ Р ) X 2 v ⁽ Р )

7

Р = 0 v

= 1.

X ₁ ( t ) =

x 1 (0) • т 1     (1 — а 1 )

Вычисление D ₃₁₁( т ) и последующих коэффициентов нецелесообразно, т. к. соответствующие им степени p в разложении S ₃( р , т ) не меньше

х J e^{pt 0} p

C 1

= X 1 (0)

(

t ₀

а ₁ - 2

а 1

т

•-----------•------------------:----------

2 ra 1 — e -^паау

X

d p х J e^{p T} p ^{а 1} d p =

C 1 +

единицы и соответствующие интегралы по замкнутому контуру равны нулю.

Таким образом,

t

V 0 7

. sin п ( а — 1) (1 - а ₁ ) •           ¹ х

х Гд — 1)Г(2 — а1)

.

п

— •    <С е^{рг 0} p "²

2га  /

| p\ = const

• Р • S з⁽ Р ^{, т )d} р = -^;

1 - а 1

* 1(0) •т • 1 а •   Кр^ 0 Р t0       2ni     , 2

⁰                      \р |= const

(1 а ₁ )

Используя свойство

Г(а1—1)Г(2 — а1) = .   ^ п sin п(а1 — 1)

гамма-функции

[9], получаем ко-

• Р • S з ⁽ Р ^{, т )d} Р ^—

нечную формулу для переходного процесса по первой координате

- X 1 ⁽⁰⁾ • ^т = ₀

t ₀

J e^{p 0} p ^a - ² _d p =

C 1 -

= — 2 • i • sln[ п ( а ' — 1)] Г ( ^ 1 — 1) • ( t 0 ) а ;

X ^а 1

^X 1id ⁽ t ) = ^X 1 ⁽⁰⁾ —-

^V t ^{0 7}

(

.

Если а , равно целому числу, то можно воспользоваться теоремой Коши о вычетах, согласно которой

f e^{z T} z" ^а 1 d z = (e — 1) ^{Г (} 2 ^{а 1)} • ( — т ) ^{а 1 — 1}

^j ’                               (1 — а 1 )

Cv +

.

Интеграл-функцию времени (21) можно вычислить и предложенным в работе методом, полагая в соответствии с формулой (18)

[ ez'-'^dz = ( e-²”¹' — ' ) ■ ^{Г (} 4⁺,¹¹ B, ( t ) =

1                                   [to

Cv +

J '

C 0 +

z а1 dz = 2ni • Re s] —— ez [ = 2ni • —

Z = 0 I z ^{а 1}

а ₁ 1

.

Г ( а 1 )

При а 1 = 2 получаем

-4^ J e^p t ⁰ Р ^^С- а ' )^d Р = у¹

1 e _{C 1}                                  t 0

и

I 1

Г e z z ²d z = Re s ^ — e ^z

1                 z = 0 [ z ²

C 0 +

= -T .

Тогда

^x 1id ^{( t )}

= - x 1 (0) • t 1        1

=       t ₀     ^ 2 П ' 1 - e ^a 1

x

x J e pt ⁰ p ^{a - 2}(1 - a 1 )d p x J e p p ^{- a} 1 d p =

C 1                                C 1*

x ^ ( 0 ) -t T

t0

Корректность формул (22) и (23) можно подтвердить непосредственным решением дифференциального уравнения, соответствующего выбранному виду определяющей передаточной функции

^{ф (} P ) = — (Рис- 3^):

p

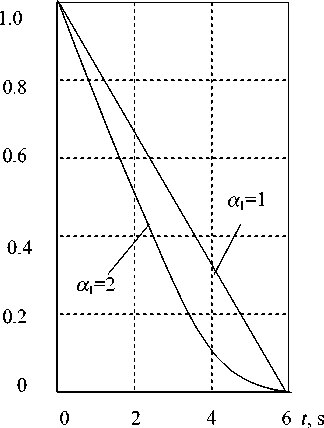
Рис. 4. Графики переходных процессов

y ⁽ t ) = ^a 1 •

y ( t )

при начальном условии y (0) = y ₀.

Уравнение (24) является дифференциальным уравнением с разделяющимися переменными, т. к. может быть приведено к виду dy       dt

— = a1---

У t ^- t 0

чения последних из условия удовлетворения ограничениям, накладываемым на характер переходного процесса. Потребуем, например, чтобы обеспечивалось заданное значение Х 1 k ускорения X 1id ( 1 0 ) в КТТ:

|x1id(t0)| - Х1 k или

Интегрируя (25), для t > t₀ получаем

In y - In y ₀ = a 1 ln( t - 1 ₀) + In C ,             (26)

x 1id ⁽ t 0 ) ^ x 1 ^{(0) -}

^a 1 ^{( a} 1 ^- 1) _{( - T} ) a 1 - 2 ^a 1        v '

t ₀

.

где С — постоянная интегрирования.

Для получения аналитического продолжения решения (26) дифференциального уравнения (20) в область интересующих нас значений t формально определим постоянную интегрирования С , исходя из начального условия y (0) = y ₀. Тогда по-

Неравенство (28) будет выполняться при любых a1> 2 и не будет выполняться при любых a1 < 2. При a1 = 2 условие (28) будет выполняться, если переходный процесс начался заблаговременно, т. е. должно выполняться ограничение лучим

C = ( - 1 0 ) " ^a 1 и y = y 0

( Oxa1

I t ⁰ '

.

1 0 ^

2 • x 1 (0) ^Х 1 к ⁽ t 0 )

Полученное методом разделения переменных решение (27) дифференциального уравнения (24)

с точностью до обозначений соответствует решениям (22) и (23), полученным другим методом — с использованием преобразования Лапласа, как

для целых, так и нецелых значений параметра a 1 .

Траектория снижения (22) будет соответствовать заданной прямолинейной траектории (заданной траектории равномерного изменения дистанции до КТТ) при a 1 = 1 и при соответствующем выборе параметров x 1 (0) = x 1 (0) _зад и 1 ₀ = 1 _0зад.

Графики переходных процессов при различных значениях a 1 представлены на рис. 4. Располагая аналитической зависимостью первой координаты от параметров x 1 (0), a 1 и 1 ₀, можно выбрать зна-

ЗАКЛЮЧЕНИЕ

В работе рассмотрены методы получения ана- литических зависимостей параметров траектории от параметров закона управления нестационарных систем с линейно меняющимися коэффициентами. Возможностью оптимизации параметров всей траектории предложенные в работе методы отличаются от известных методов оптимизации параметров конечного положения нестационарных динамических объектов. Приведенный пример подтверждает корректность решения задачи Коши методом, основанным на использовании преобразования Лапласа, и корректность предложенного метода вычисления интегралов — функций времени, входящих в структуру решения задачи Коши.