Динамика перепутывания атомов с двухфотонными переходами, индуцированного тепловым полем

Перепутанные состояния являются фундаментом современной квантовой информатики, поскольку используются для реализации эффективных физически стойких протоколов квантовых вычислений, квантовой телепортации и квантовой коммуникации, квантовой криптографии и др. [1–3]. Для квантовых вычислений и квантовой связи нужны максимально перепутанные, устойчивые состояния с большими временами декогеренции. В связи с этим в задачу современной квантовой информатики и квантовой оптики входит создание эффективных методов генерации и управления перепутанными состояниями, а также изучение различных физических систем, которые могут быть использованы в качестве кубитов квантовых устройств. Для генерации атом-атомных перепутанных состояний может использоваться их взаимодействие с общим полем (электромагнитным, фононным и т.д.) резонатора. Степень перепутывания атомов, возникающая за счет взаимодействия с полем резонатора, кроме особенностей структуры атома и резонатора и силы их связи, зависит также от большого числа других факторов, в частности, от состояний, в которых приготовлены изначально атомы и поле, наличия различных каналов диссипации энергии, фазы и т.д. Естественные и искусственные атомы (нейтральные ридберговские атомы и ионы в ловушках, при- месные спины, квантовые точки, сверхпроводящие кольца с джозефсоновскими переходами, гибридные и оптомеханические системы), взаимодействующие с выделенными модами резонаторов, в настоящее время исследуются не только теоретически, но и реализованы экспериментально в различных системах квантовой электродинамики резонаторов (РКЭД) [4, 5]. Для теоретического описания таких систем обычно используется модель Джейнса–Каммингса (МДК) и её обобщения [6–8]. Модели типа Джейнса– Каммингса играют фундаментальную роль в квантовой оптике и квантовой информатике, поскольку позволяют описать все основные квантовые эффекты взаимодействия излучения с веществом: вакуумные осцилляции Раби, затухание и восстановление осцилляций Раби, антигруппировку фотонов и субпуассоновскую статистику поля резонатора, сжатие света, сверх- и субизлучение, атом-атомное и атом-полевое перепутывание, мгновенную смерть перепутывания и другие [6–8]. Все эти эффекты удалось экспериментально наблюдать в системах РКЭД [4, 5]. Многие эксперименты с системами РКЭД показали, что МДК и ее обобщения, учитывающие многоатомность, мно-гоуровневость, расстройку частот кубитов и поля и другие особенности системы, дают прекрасные описания динамики кубитов и поля резонатора [9– 15]. При этом согласие между теоретическими и экспериментальными результатами имеет место не только для динамики средних населенностей уровней энергии кубитов, среднего числа фотонов в резонаторе и их корреляционных функций [9– 14], но и для динамики параметров перепутывания [15]. Ранние эксперименты с РКЭД в значительной степени ограничивались режимом слабой связи между кубитом и полем резонатора, то есть ситуацией, когда константа кубит-полевого взаимодействия много меньше частоты перехода в кубите. Однако в последние годы за счет улучшения конструкции резонаторов, эффективных методов лазерного охлаждения, а также использования искусственных атомов, таких как сверхпроводящие джозефсоновские кольца или примесные спины, удалось сместить границы экспериментальных исследований в сторону режима сильной и уль-трасильной связи, когда константа кубит-полевого взаимодействия сравнима с частотой перехода в кубите [16], что позволило наблюдать новые физические явления, такие как рождение фотонных пар или двухфотонное поглощение при интенсивностях, значительно ниже уровней, на которых нелинейные переходы обычно происходят [17]. Для теоретического описания таких систем необходимо использовать нелинейные версии модели Джейнса–Каммингса, в частности, модели с двухфотонными переходами [18, 19]. Такие модели были с успехом использованы для описания экспериментов в РКЭД для ионов в ловушках Пауля [20], нейтральных атомов [21], квантовых точек [22] и в сверхпроводящих цепях [23, 24]. Двухфотонная модель Джейнса–Каммингса успешно применялась также и для описания перепутывания сверхпроводящих кубитов в копланарном резонаторе [25]. Важным достоинством двухфотонной модели Джейнса– Каммингса является то, что она имеет точное решение, что позволяет проводить детальный анализ динамики систем с двухфотонными переходами. Однако в последнее время для описания систем РКЭД в режиме ультрасильной связи широко применяется обобщение модели Джейнса–Каммингса, не использующее приближение вращающейся волны, так называемая модель Раби. Указанная модель успешно используется для описания сверхпроводящих кубитов в резонаторе [26]. Недавно в работе [27] предложена твердотельная сверхпроводящая схема в виде джозефсоновских кубитов в резонаторе, в которой кубит и резонатор связаны двухфотонным взаимодействием, для реализации двухфотонной модели Раби.

Взаимодействие квантовых объектов, приготовленных в перепутанном состоянии, с окружением обычно приводит к декогерентности и потере особых квантовых корреляций состояний или перепутывания. Это означает, что основная проблема, возникающая при создании, контроле и хранении атомных перепутанных состояний, заключается в том, чтобы предотвратить, минимизировать или использовать влияние шума. Было высказано большое количество предложений по защите, минимизированию или использо- ванию влияния окружения для создания и сохранения максимально перепутанных состояний, например, стратегия кольцевого контроля, коррекция квантовых ошибок, использование избыточного кодирования и др. [1 –3]. Однако указанные способы успешно решают проблему только при малой скорости генерации ошибок в исследуемой системе, а также чрезвычайно сложны при экспериментальной реализации. Недавно в большом количестве работ было показано, что в некоторых случаях диссипация и шум могут, напротив, являться источником перепутывания [28]. В частности, была предсказана возможность генерации перепутывания кубитов и поля за счет взаимодействия кубитов с тепловым полем резонатора [29]. Питер Найт с соавторами [30] показали, что одномодовый тепловой шум может индуцировать атом-атомное перепутывание в системе двух двухуровневых атомов в идеальном резонаторе. В последнее время, как уже отмечалось выше, в квантовой информатике особое внимание уделяется изучению динамики кубитов, взаимодействующих с электромагнитными полями посредством двухфотонных процессов в связи с высокой степенью корреляций состояний испускаемых фотонов. Перепутывание в двухатомной системе с вырожденным двухфотонным взаимодействием, индуцированное одномодовым тепловым шумом, было рассмотрено в работе [31], а влияние двухмодового теплового шума на перепутывание двух двухуровневых атомов с невырожденными переходами и переходами рамановского типа ‒ в работе [32]. При этом было показано, что при двухфотонном взаимодействии степень перепутывания атомных состояний может значительно превосходить соответствующую величину для однофотонного взаимодействия. В [33] были обобщены результаты работы [30] на случай нерезонансного однофотонного взаимодействия атомов с тепловым полем резонатора. При этом было показано, что наличие расстройки частот атомов и поля приводит к существенному возрастанию степени перепутывания, индуцированного тепловым полем. В указанной работе также была предсказана возможность перепутывания атомов, приготовленных в начальный момент времени в возбужденных состояниях. Позднее динамика перепутывания кубитов, индуцированного тепловым полем, при наличии ди-поль-дипольного взаимодействия, атомной когерентности, расстройки частот атомов и поля и других механизмов изучалась в работах [34–45]. Принимая во внимание особый интерес, который в последнее время сфокусирован как на экспериментальных [27–29], так и на теоретических исследованиях [46–54] перепутывания кубитов в системах РКЭД с двухфотонными переходами, в настоящей работе мы исследовали особенности перепутывания двух атомов (кубитов) в рамках нерезонансной двухатомной двухфотонной модели Джейнса–Каммингса с тепловым полем резонатора. Экспериментально динамика резо- нансного взаимодействия многоуровневого искусственного атома (транзмона) со слабым тепловым полем копланарного резонатора изучалась в работе [54]. При этом авторы установили, что полученные результаты хорошо описываются в рамках обобщенной многоуровневой модели Джейнса–Каммингса. Поскольку расстройка частот атома и поля может существенно увеличивать степень перепутывания кубитов [33], мы уделили особое внимание изучению влияния расстройки частот атомов и поля на максимальную степень перепутывания кубитов.

Таким образом, в настоящей работе мы исследуем динамику перепутывания двух двухуровневых атомов, нерезонансно взаимодействующих посредством вырожденных двухфотонных переходов с одномодовым тепловым полем идеального резонатора, для сепарабельных и перепутанных начальных состояний атомов.

1.    Модель и её точное решение

Будем исследовать систему, состоящую из двух идентичных естественных или искусственных двухуровневых атомов (кубитов) с резонансной частотой перехода ω 0 , взаимодействующих с квантовым электромагнитным полем идеального резонатора посредством вырожденных двухфотонных переходов. Физически это могут быть ридберговские нейтральные атомы, ионы в ловушках Пауля, сверхпроводящие джозефсоновские кольца, примесные спины, квантовые точки и другие двухуровневые системы, взаимодействующие с микроволновыми полями резонаторов или сверхпроводящими LC-контурами. Эффективный гамильтониан такой системы в системе отсчета, вращающейся с удвоенной частотой моды поля резонатора 2 ω , можно записать в виде

H = (1/ 2)h & ( a Z + a 2 ) + ^ g ^ ( a + a ² + a ^{+ 2} a - ), (1) i =1

где σiz ‒ оператор инверсии населенностей в i-м атоме (i = 1, 2), σi+ =| +〉ii 〈-| и σi- =| -〉ii〈+| ‒ повышающий и понижающий операторы в i-м атоме, | + 〉i и |– 〉i ‒ возбужденное и основное состояние двухуровневого i-го атома, a и a+ ‒ операторы рождения и уничтожения фотонов (или плазмонов в случае LC-резонатора) резонаторной моды, g ‒ константа эффективного двухфотонного взаимодействия атомов с полем резонатора и Δ ‒ расстройка частоты атомного перехода и удвоенной частоты резонаторной моды, равная Δ = ω0–2ω. Очевидно, что пригодность перепутанного состояния для целей квантовых вычислений или квантовых коммуникаций определяется соотношением времени, необходимого для произведения с кубитом требуемых операций и временами диссипативных процессов в системе. При выборе модели мы не приняли в расчёт диссипативные процессы, учитывая, что в настоящее время для исскуственных атомов в копланарных резонаторах (электронных и ядерных примесных спинов и сверхпроводящих джозефсоновских кубитов) время декогеренции во много раз превосходит времена операций с кубитами [2, 3]. Так, например, в одном из недавних экспериментов по исследованию динамики сверхпроводящих джозефсо-новских кубитов с двухфотонными переходами в резонаторе [27] частота моды поля составляла примерно 5 ГГц, константа двухфотонного кубит-полевого взаимодействия равнялась g/ω = 0,01, в то время как скорость потерь фотонов из резонатора была γ /ω = 10–3, скорость спонтанного излучения кубитов κ /ω = 10–4, а скорость диссипации фазы Г/ω = 10–5. Параметры кубитов, частоты мод и константы диссипации для многочисленных экспериментов по исследованию взаимодействия кубитов с микроволновыми полями приведены в недавнем обзоре [29].

Мы будем исследовать динамику системы как для начальных сепарабельных

| Ψ(0)〉A =|+, -〉,(2)

| Ψ(0)〉A =| +,+〉,(3)

так и для перепутанного состояния белловского типа

| Ψ(0)〉A =cosθ|+,-〉+sinθ|-,+〉,(4)

где θ ‒ параметр, определяющий начальную степень перепутывания атомов (0 ≤ θ ≤ π ). При этом максимальной степени перепутывания атомов соответствует значение θ = π /4.

В качестве начального состояния поля резонатора будем рассматривать тепловое состояние

ρF(0) = ∑pn| n〉〈n|, n nn

p n

(1 + n ) ^{n ,}

где n ‒ среднее число фотонов в резонаторной моде, n (exp[ A« / k_BT ] - 1] ^{- 1}, k_B - постоянная Больцмана и T ‒ равновесная температура резонатора.

Найдём точную динамику представленной модели. Начнём исследование для случая, когда резонаторное поле приготовлено в состоянии с определённым числом фотонов, а затем обобщим полученные результаты на случай теплового поля резонатора. Для фоковского начального состояния поля и чистых начальных состояний атомов в процессе эволюции рассматриваемой системы её состояние по-прежнему будет определяться волновой функцией. Решение временного уравнения Шредингера для полной волновой функции системы iй d I ^(t)) = h । ^(t))

∂t будем искать в виде

| Т ( t ) ) = e - i^Ht / * | ^ (0) ) ,

где ^Р(0) ) - начальная волновая функция полной системы. Начальную волновую функцию полной системы можно представить в виде разложения по собственным функциям гамильтониана (1) («одетым состояниям»). Пусть число элементарных возбуждений в системе с гамильтонианом (1) есть n ( n >  0). Тогда собственные функции гамильтониана (1) могут быть представлены в виде

| ^Ф in ⁾ = ^K in ^{( ц} i 1 n | ^— , - , n + ^{4 )} + ^ц 2 n | + , ^— , ⁿ + ^{2 )} + +Ц i 3 n ^{1 —} , + , ^{n + 2 ) +} Ц i 4 n ^{1 +} , ⁺ , ⁿ ) ), ⁽ i = ^1,2,3,4) ,

где

K in = 1 / V| Цл n | 2 + | Ц 2 n | 2 + | Ц , -3 n | 2 + | Ц 4 n | 2 и

Ц 11, n = 0,    Ц 12, n --1, ^ц 13, n =1, Ц 14, n = 0,

2д/2 + 3 n + n ² V12 + 7 n + n ² 24 + 14 n + 2 n ² — 5s in — s ² _n

^ц / 2, n     Ц 1 '3, n

л] 2 + 3 n + n ² ( 5 + s in )

24 + 14 n + 2 n ² —5s ,n — s " ’

ц , 4, n =1 ( i = 2,3,4),

где 5 = A / g .

Сооответствующие безразмерные собственные значения гамильтониана есть

S 1 n =0, s 2 n = — Re

1/3

( Yn — 'v  X ) ,

X X n               '_

S 3 n =Re

----¹----1 — i43\Y — (1 + i4з\X 2 /2^2/3 3 x 2^2/3 X_n ⁽⁽         ) n ⁽         ) n )

S 4 n =Re

где

----¹----((1 + i 73^ Y — (1 — i V3) X 2 / 2^2/3 3 x 2^2/3 X_n ¹¹          ) n ⁽          ) n )

X n = ( Z n + V Z " + 4 Y n ³ ) ^1/3,

Y n = — 84 — 60 n — 12 n ² — 3 5 ²,

Z_n = — 216 5 (5/2 + n ).

Здесь s _in = E_inIhg ( i =1,2,3,4). Заметим, что в случае нерезонансной модели все собственные значения различны, так как параметр X n является комплексным числом. Поскольку в дальнейшем мы будем сравнивать поведение резонансной и нерезонансной моделей, приведём также значения безразмерных уровней энергии полной системы для случая резонансной модели

s 1 _n =0, s _{2 n} =0, s _{3 n} = — 2V7 + 5 n + n ²,

s _{4 n} = 2V7 + 5 n + n ².

Наконец, приведём для иллюстрации значения безразмерных энергий полной нерезонансной системы в случае 5 = 1, n = 0:

s 10 = 0; s 20 = 0,70; s 30 = -5,70; s 40 = 5

и 5 = 1, n = 1:

s 10 = 0; s 20 = 0,53; s 30 = -7,53; s 40 = 7.

В случае резонанса соответствующие выражения для уровней энергии примают следующие значения:

0, 0, –5,29, 5,29 и 0, 0, –7,21, 7,21.

Таким образом, учитывая, что e—iH‘/* | Ф,„) = e—iE""/* | Ф,„), в представлении одетых состояний временная часть полной волновой функции будет в общем случае представлять собой суперозицию временных функций вида е-Е"1/h (i = 1,2,3,4).

Предположим, что начальное состояние исследуемой системы есть | +, -, n +2 ) ( n >  0). Тогда в момент времени t состояние системы можно описать вектором состояния

| ^ ⁽ " ) ) = G 12,n | ^— , ^— , ^{n + 4 ) +} G 22, n | ⁺ , ^— , ^{n + 2 ) +}

+ G32,n | —, +, n + 2) + G42,n | +, +, n) , где

G i 2, n = e ^{— i s} ' n t / * K 1 n ц * 2 n Ц 1 ," + e ^{— i s 2} n t / * K n Ц , *2 n Ц 2™ +

+ e - i ^s 3ⁿ " / * K 3 n Ц *2 n Ц 3 ," + e ^{— i s} 4^nt / * K 4 n ц , *2 n Ц 4 ," , ( i =1,2,3,4).

Если же начальное состояние системы есть | +, -, 0 ) или |+,-,1 ) , то временная волновая функция имеет вид

| * ( " ) ) =

= G 1 ⁽ 2) | — , — , 2 ) + G 22) | + , — , 0 ) + G 32) | — , + , 0 ) ,

где

G 1 ⁽ 2) ( t ) = — 2 V² ie i ^{5 /2}

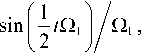
G 22) ( t ) = 2 U + e ^{i 5} " ^/2

G 32) ( t ) = 2 J 1 — e i ⁵ t ^/2

или

cosf ^ t | — i ( 5 / Qi )sinf^ 1 t

I 2 J I 2

cos I ^1 t | — i ( 5 / Qi )sin I ^1 t

I 2 J I 2

| ^ ( t ) ) =

= G 1 ⁽ 2 ²⁾| — , — ,3 ) + G 22) | + , — ,0 ) + G 3 ⁽ 2) | — , + ,0 ) ,

где

G^Ct ) = - 2Тб ie i ^{6 /2}

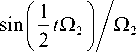
G£( t ) = j 1 1 + e * ^/2

cosf ^t |-i(6/Q[)sin| ^t l 2 J I 2

g 244 1 ) =

2V ² ie* ⁶ t ^/2 sin 1 2 Q , t

Q 1

G§( t )=j 1 1 - e * ^/2

cos

-

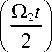
i ( 6 / Q 1 )sin

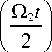
g 'U'c t ) = g 24) ( t )

или

Предположим, что наша система в начальный момент находится в состоянии |-,+, n +2 ) ( n >  0). Тогда временная волновая функция может быть представлена в виде

| * ( t ) ) =

= ^G 1 ⁽ 4 ^{) | -} , ^- , ^{3 ) + G} 24) ^{| +} , ^{- ,1 ) + G} 34) ^{| -} , ^{+ ,1 )} ,

где

^ ⁽ t ) ) = G 13, n | ^- , ^- , ⁿ + ^{4 )} + G 23, n | + , ^- , n + ^{2 )} +

+ ^G 33, n ^{1 -} , ⁺ , ⁿ + ^{2 )} + ^G 43, n ^{1 +} , ⁺ , ^{n )} ,

где коэффициенте G i ₃, _n имеют вид (8) при замене ц *2 n на ц *3 n ( i =1,2,3,4).

Если же начальное состояние системы есть |-,+,0 ) или | -, +, 1 ) , то временная волновая функция примет вид

G ®( t ) = e - ⁶ t ^/2

g 24) ( t ) =

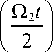
it 6		1 1 q2 L 2 2 J
2д/6 ie2	sin

Q 2

G ._:' ( t ) = g 22) ( t )

+ i ( 6 / Q ₂ )sin

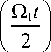
I * ( t ) ) =

= G ™ | - , - , 2 ) + G 23) | + , - , 0 ) + G £> | - , + , 0 ) ,

соответственно. Выше мы использовали обозначения

Q 1 = V16 + 6 ², Q ₂ = V48 + 6 ².

где

G ^ ( t ) = G 1 ⁽ 2) ( t ), G 23) ( t ) = G ™, G ™ ( t ) = G 22 или

I * ( t ) ) =

= G 1 ⁽ 3 ²⁾ I - , - , 3 )+ g 22) I + , - ,1 ) + g® I - , + ,1 ) ,

где

G 1 ⁽ 3 ²⁾ ( t ) = G ( t ), G 22) ( t ) = G 32) ( t ),    G 223 ( t ) = G 2? ( t )

соответственно.

Для начальных состояний |+,+, n ) и |-,-, n +4 ) временные волновые функции есть

¹ ^ ⁽ t ^{) )} = ^G 11, n ^{1 -} , ^- , ⁿ + ^{4 )} + ^G 21, n ¹ + > ^- , ⁿ + ^{2 )} + + ^G 31, n ^{1 -} , + > ⁿ + ^{2 )} + ^G 41, n ¹ + > + > ^{n )} ,

¹ ^ ⁽ t ^{) )} = G 14, n ^{1 -} , ^- , ^{n + 4 ) + G} 24, n ^{1 +} , ^- , ^{n + 2 )} + + G 34, n ^{1 -} , + > ⁿ + ^{2 )} + ^G 44, n ¹ + > + > ^{n )} .

Коэффициенты G i 1, _n ( G i 1, _n ) могут быть получены из (8) путём замены ц *_{2 n} на ц * 1 _n ( ц *_{4 n} ) ( i =1,2,3,4).

Если начальное состояние системы | -, -, 2 ) или | -, -, 3 ) , временную волновую функцию можно представить как

। ^ t ) ) =                                        (16)

= G^b-,2) + G24) |+,-,0) + G«|-, +,0), где

G ff( t ) = e ^{i 6} t ^/2

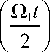
+ i ( 6 / Q 1 )sin

Наконец, для начальных состояний | -, -, 2 ) и | -, -, 0 ) временные волновые функции есть

| Y ( t ) ) = e - ^{i 6} t | - , - ,1 )                                      (18)

или

| * ( t ) ) = | - , - ,0 )                                      (19)

соответственно. Используя выражения (6)-(19), мы можем найти явный вид матрицы плотности полной системы р Fock ( t ) = | ^ ( t ) )(^ ( t )|. Используя выражение для матрицы плотности в случае фоковского начального состояния поля, легко получить явный вид матрицы плотности полной системы для теплового поля р Thermal ( t ). Выполняя усреднение полной матрицы плотности по переменным резонаторного поля, мы можем получить редуцированную матрицу плотности подсистемы атомов (кубитов) р A ( t ) = Tr F р Thermal ( t ). Атомная матрица плотности может быть использована для вычисления параметра перепутывания атомов.

2.    Вычисление параметра перепутывания атомов

В качестве параметра перепутывания атомов мы воспользуемся параметром Переса-Хородецких или отрицательностью, которая может быть представлена в терминах отрицательных собственных значений ц - частично транспонированной по переменным одного кубита атомной матрицы плотности ( р T )

е = -2] ^ ц - .

Для сепарабельных начальных состояний кубитов (2), (3), а также перепутанного состояния белловского типа (4) редуцированная атомная матрица плотности имеет вид

	"P 11 ( t ,      0         0        0 Л
	0       P 22 ( t )    р 2з ( t )     0
P A ( t ) =		.          (20)
	0 P 23 ( t ) *    Р зз ( t )     0
	^ 0        0        0      p 44 ( t )

Элементы матрицы (20) для начального состояния кубитов вида | +, -) можно записать в виде от

P11(t) = ZPn I G42.n-2(t) |2, n=2

от

P 22 ( t ) = Z P n । G 22. n — 2 ( t ) I² + P 1 G 2 ^2,( t ) 2 + P 0 G 22 ( t ).

n =2

от

Р зз ( t ) = Z P n I G 32.n - 2 ( t ) I² + P 1 G З^ t ) 2 + P 0 G 32 ⁾( t ), n =2

от

P 44 ( t ) = Z P n । G 12. n — 2 ( t ) I^{2 +} P 1 Gn (-1 ) 2 ⁺ P 0 G 2) ( t ), n =2

от

P23 ( t ) = ZPnG22. n—2( t)( G32. n-2 )* ( t) + n=2

+ p g 21) ( t )( g® , * ( t , + P 0 g 22) ( t )( g^ , * ( t ,.

Для начального состояния | +, + } соответствующие матричные элементы есть

P 11 ( t ) = от                                                      от

= Z P n I G 41. n ( t , I², P 22 ( t ) = Z p n I G 21. n ( t , I², n =2                                   n =2

от                                                      от

P 33 ( t ) = Z P n I G 31. n ( t ) I², P 44 ( t ) = Z P n I G 11, n ( t ) I², n =2                                n =2

P 23 ( t ) = Z P n G 21, n ( t ) G 3*1, n ( t ).

n =2

Для перепутанного состояния вида (4) матричные элементы в настоящей работе не приводятся ввиду их достаточно громоздкого вида.

Частично транспонированная по переменным одного кубита матрица плотности для (20) может быть записана в виде

T	'P 11 ( t ) 0	0 P 22 ( t )	0 0	p 23 ( t )
				0	.         (21)
P A1 ( t ) =	0	0	Р зз ( t )	0
	4 p 23 ( t )	0	0	P 44 ( t ) ;

Матрица (21) имеет всего одно собственное значение, которое может быть отрицательным. В результате для отрицательности имеем

S ( t ) = 7( P 11 ( t ) -P 44 ( t ))² + 4 I Р 2з ( t ) I² -

— P 11 ( t ) -P 44 ( t ).

Результаты численного моделирования отрицательности (22) представлены на рис. 1–4.

3.    Результаты и обсуждение

Отрицательность для сепарабельного начального атомного состояния (2) показана на рис. 1 как функция безразмерного времени gt для малых расстроек и фиксированного значения среднего числа фотонов n =0,1. Из рис. 1 видно, что увеличение безразмерного параметра расстройки 5 приводит к существенному увеличению максимальной степени перепутывания кубитов. В случае больших значений расстройки между атомами и модой поля отсутствует обмен энергией реальными фотонами. Атомы обмениваются виртуальными фотонами, в результате такая возбужденная виртуальная среда резонатора приводит к усилению квантовых корреляций или перепутанности состояний атомов. Аналогичный эффект для модели с однофотонными переходами отмечался в работе [35].

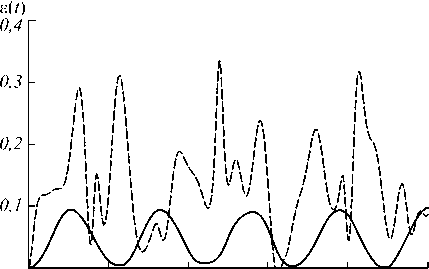
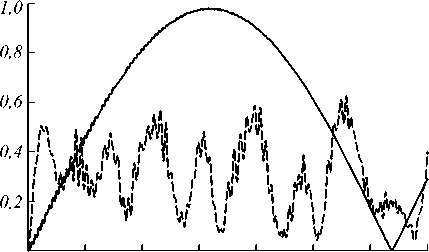
На рис. 2 приведено сравнение поведения параметра перепутывания для резонансной (сплошная линия) и нерезонансной (штриховая линия) однофотонной (рис. 1 а ) и двухфотонной (рис. 2 б ) моделей. Очевидно, что при малых средних числах фотонов основной вклад в суммах для элементов матрицы (21) и, соответственно, в параметр перепутывания (22) будут давать временные слагаемые, содержащие экспоненциальные множители e^{iEin t / ħ} ( i = 1,2,3,4) с n близкими нулю. Для резонансной модели при любых n два уровня энергии полной системы обращаются в ноль, а два других отличаются только знаком, поэтому поведение наблюдаемых сохраняет осцилляторный характер. В случае нерезонансной модели все уровни энергии различны для всех значений n (при этом один из них нулевой), что приводит к существенной нелинейности в поведении наблюдаемых. Аналогичное различие в поведении наблюдаемых для резонансной и нерезонансной моделей с однофотонными переходами отмечалось ранее в работе [33].

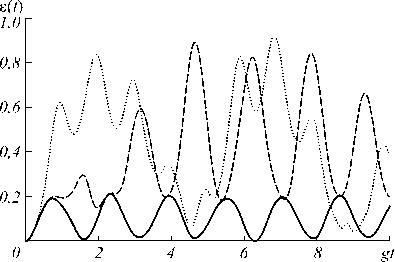
Рис. 1. Отрицательность как функция безразмерного времени gt для начального атомного состояния (2).

Безразмерный параметр расстройки 5 =0 (сплошная линия), 5 =0,5 (штриховая линия) и 5 =5 (точечная линия).

Среднее число тепловых фотонов n =0,1

В настоящее время имеется большое число экспериментов по перепутыванию как двух, так и многих кубитов различной физической природы за счёт вза- имодействия с полями микроволновых резонаторов (сверхпроводящих джозефсоновских колец, ионов в магнитных ловушках, ридберговских атомов и др.) [29]. При этом основное внимание уделяется экспериментам со сверхпроводящими кубитами, поскольку они в настоящее время наиболее широко используются в качестве логических элементов квантовых компьютеров. При этом на основе экспериментов удается определить не только усредненные значения параметра перепутывания кубитов, но и полную зависимость параметра перепутывания от времени [15]. В экспериментах по перепутыванию сверхпроводящих кубитов использовались вакуумные поля резонаторов и однофотонные взаимодействия. Однако, как уже отмечалось выше, динамика населённостей сверхпроводящих кубитов с двухфотонными переходами и среднего числа фотонов в моде резонатора также активно исследуется экспериментально в последние годы [27, 28]. Характеристики сверхпроводящих кубитов с многофотонными переходами приведены в обзоре [28]. Параметры эксперимента [27] приведены нами при описании использованной в работе модели. Как уже отмечалось во Введении, в работе [54] экспериментально также изучалась динамика резонансного взаимодействия сверхпроводящего кубита (транзмона) со слабым тепловым полем копланарного резонатора. Таким образом, по мере совершенствования техники эксперимента возможно будет наблюдать динамику перепутывания кубитов с двухфотонными переходами в резонаторах со слабым тепловым полем и изучить влияние расстройки на степень перепутывания кубитов.

е(')

а) О 2        4        6         8 gt   б) О 5     10    15    20    25    30 gt

Рис. 2. Отрицательность как функция безразмерного времени gt для начального атомного состояния (2) в случае однофотонной двухатомной (а) и двухфотонной двухатомной (б) МДК. Безразмерный параметр расстройки δ =0 (сплошная линия) и δ =10 (штриховая линия). Среднее число тепловых фотонов n =0,1

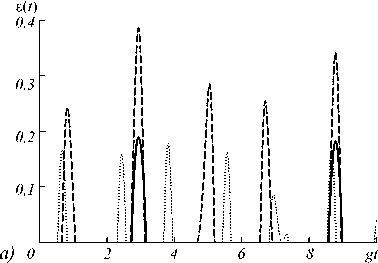
Из рис. 2а видно, что для резонансного взаимодействия атома с полем перепутывание, индуцированное нелинейным двухфотонным взаимодействием с тепловым шумом резонатора, больше, чем перепутывание, вызванное линейным однофотонным взаимодействием. Такой результат впервые для резонансной двухатомной двухфотонной модели получен в работе [31]. Однако, как видно из рис. 2б, полученного из (22), ситуация принципиально меняется для модели с нерезонансным взаимодействием. В последнем случае перепутывание атомов, индуцированное двухфотонным взаимодействием, существенно меньше, чем перепутывание, индуцированное однофотонным взаимодействием атомов с полем. Отрицательность для сепарабельного начального атомного состояния (3) изображена на рис. 3 как функция безразмерного времени gt для различных расстроек и фиксированного значения среднего числа фотонов n =0,1 (рис. 3a) и n =1 (рис. 3б). В работах [30–43] было показано, что резонансное одно- и двухфотонное взаимодействие атомов, приготовленных одновременно в возбуждённом состоянии, с тепловым полем резонатора не приводят к их перепутыванию ни для каких параметров модели. Однако ситуация принципиально ме- няется для двухатомной модели с нерезонансным взаимодействием. Из рис. 3 видно, что для нерезонансного взаимодействия перепутывание кубитов, приготовленных первоначально в возбуждённых состояниях, возможно при малых средних числах тепловых фотонов n ≤ 1 .

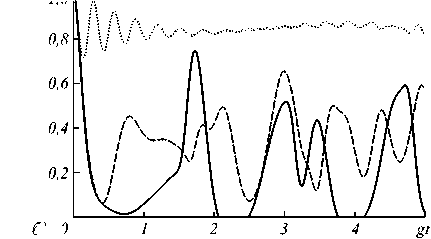
Временная зависимость отрицательности для перепутанного начального атомного состояния (4) представлена на рис. 4 как функция безразмерного времени gt для фиксированного значения среднего числа фотонов n =0,1 (3 a ) и n =1 (3 б ). Из рис. 4 хорошо видно, что включение расстройки частот атомов и поля уменьшает осцилляции параметра перепутывания, т.е. приводит к стабилизации начального атомного перепутывания по отношения к флуктуациям, вызванным тепловым шумом. Как и в случае сепарабельных начальных состояний атомов, для больших расстроек возбуждённая виртуальная среда резонатора не разрушает начальные квантовые кореляции или перепутанность состояний атомов. Аналогичный эффект имеет место для ридберговских атомов, приготовленных в белловских перепутанных состояниях и последовательно пролетающих вакуумный или тепловой резонатор одноатомного мазера [55].

Е«)

0,14

0,12

0,10

0.08

0,06

0,04

0,02

б)   О

Рис. 3. Отрицательность как функция безразмерного времени gt для начального атомного состояния (3). Безразмерный параметр расстройки δ =1 (сплошная линия), δ =3 (штриховая линия) и δ =5 (точечная линия).

Среднее число фотонов n =0,1 (a) и n =1 (б)

На рис. 4б показано, что для резонансного взаимодействия кубитов и поля в случае достаточно интенсивного теплового поля имеет место эффект внезапной смерти перепутывания. Однако указанный эффект легко может быть устранён путём включения небольшой расстройки частот атомов и поля. Такое действие легко может быть выполнено для многих типов кубитов, в частности, для сверхпроводящих ку- битов, у которых энергетическая щель между основным и первым возбуждённым уровнем легко может изменяться при изменении магнитного поля. Таким образом, отстраивая частоты кубитов от частоты резонаторного поля, для изначально перепутанных кубитов мы можем значительно уменьшить осцилляции параметра перепутывания, возникающие за счёт их взаимодействия с тепловыми фотонами резонатора.

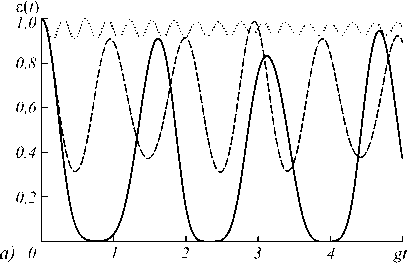
Рис. 4. Отрицательность как функция безразмерного времени gt для перепутанного начального атомного состояния (4). Безразмерный параметр расстройки δ =0 (сплошная линия), δ =5 (штриховая линия) и δ =20 (точечная линия). Среднее число фотонов n =0,1 (a) и n =1 (б)

E(Z) i.ov

б) о

Заключение

Таким образом, в настоящей работе мы исследовали влияние расстройки частот атомов и поля на перепутывание естественных или искусственных атомов, нерезонансно взаимодействующих посредством вырожденных двухфотонных переходов с тепловым одномодовым полем идеального резонатора. Мы показали, что для сепарабельного начального состояния атома |+,–〉 малые расстройки могут значительно увеличить степень перепутывания атомов, индуцированную тепловым полем. Расчёты временной за-висмости отрицательности показали, что для нерезонансного взаимодействия атома с полем степень атом-атомного перепутывания, индуцированного нелинейным двухфотонным взаимодействием, меньше, чем перепутывание, индуцированное однофотонным взаимодействием, в отличие от обратной ситуации в случае резонансного взаимодействия. В последнем случае, как было показано ранее, перепутывание, вызванное нелинейным взаимодействием, больше, чем перепутывание, вызванное линейным взаимодействием. Мы также показали, что в случае нерезонансного взаимодействия для сепарабельного начального состояния |+,+〉 тепловое поле может индуцировать атом-атомное перепутывание в случае достаточно малых интенсивностей теплового поля. Расчёты также показали, что для перепутанного начального атомного состояния типа Белла расстройка частот атомов и поля приводит к существенному уменьшению амплитуд колебаний отрицательности, то есть приводит к стабилизации начального перепутывания. В случае относительно интенсивных тепловых полей включение расстройки позволяет устранить эффект мгновенной смерти перепутывания. В настоящей работе нами не учитывались эффекты диссипации энергии в рассматриваемой системе. Такое рассмотрение на основе кинетической теории в рамках марковского [56] или немарковского [57] приближений будет предметом нашей следующей работы.