Динамика пластины с упруго присоединённой массой

В современной механике твердого деформируемого тела задачи нагружения пружины вызывают особый интерес. В бампере транспортного средства, в турникетной опоре железнодорожного средства пружина и прикрепленные к ней устройства служат для гашения энергии удара, в витринном устройстве пружина с объектом на ней используется для выталкивания товаров. В работе [1] рассматривается задача о совместных колебаниях твердого тела, упруго присоединенного к неоднородной двухступенчатой балке в двух точках закрепления. В работе [2] исследованы механические колебания твердого тела, соединенного упругими связями со стержнем. Эти задачи были решены посредством вариационного принципа Гамильтона. В данной работе рассматривается задача, где в отличие от предыдущих работ, один конец балки не является закрепленным, а также, решение находится с помощью интегрального преобразование Лапласа [3-4] по времени. Для численного решения обратного преобразования применяется метод Дурбина [5, 6]. Аналитическое и численное решение сравнивается путем сверки на малом промежутке времени.

Пластиной называют тело, которое в не-деформированном состоянии является прямоугольным параллелепипедом, в котором один из размеров (толщина пластины – h) много меньше двух остальных. Учитывая малую толщину, кинематику движения материальных точек пластины можно свести к движению точек, изначально находившихся на срединной плоскости (рис. 1). Ось z направим по нормали к срединной плоскости, ось х — по длине пластины (L —длина), ось у —по ширине (2а — ширина). Ограничимся случаем цилиндрического изгиба, при котором перемещения не зависят от координаты у.

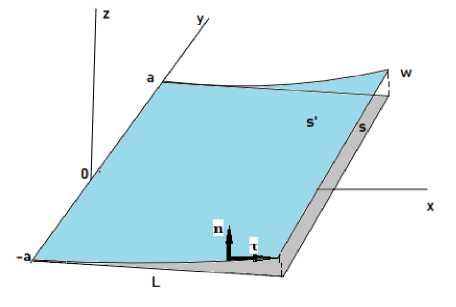
Рисунок 1 - Схема деформирования пластины: S – недеформированная срединная плоскость пластины, S’ – положение точек срединной поверхности после цилиндрического изгиба, 2d —ширина пластины, L —длина пластины, n, т —вектор нормали и касательной к образующей цилиндрической поверхности

Материалы и методы

При цилиндрическом изгибе геометрия пластины фактически задается кривой её срединного волокна в любом сечении у — const. На любой выделенный элемент действует система сил и моментов. Рассмотрим уравнения равновесия пластины, считая, что на неё действуют массовые силы с плотностью G(s, t) и распределенные по поверхности силы с линейной плотностью q(s, t), где s — длина дуги срединного волокна балки 0 < s < L, t —время. Примем в качестве начального состояния, недеформированное горизонтальное положение и будем считать, что срединное волокно не меняет своей длины.

Введём в рассмотрение материальные координаты s,y, ?, вмороженные в упругую среду. В начальном, недеформированном состоянии координата s совпадает с координатой %, координата ? - с координатой z. Примем гипотезу плоских сечений, согласно которой начальные сечения x=const после деформации остаются ортогональными изогнутому нейтральному волокну (Рисунок 2 a-b). В данных предположениях единственной, отличной от нуля деформацией будет растяжение волокна, изначально параллельного координате s. Пусть после изгиба нейтральное волокно составляет в каждой локальной точке с координатой s угол p(s) с осью %. Тогда векторы нормали и касательной (Рисунок 1) можно записать в следующей форме:

т — e_X cos p + e_z sin p , n = —e_X sin Ф + e z cosp (1)

Тогда относительное удлинение (деформацию) волокна с координатой ? можно выразить при помощи радиуса кривизны нейтрального волокна, для которого ? — 0:

? 1 dp

E —RR—ds ,

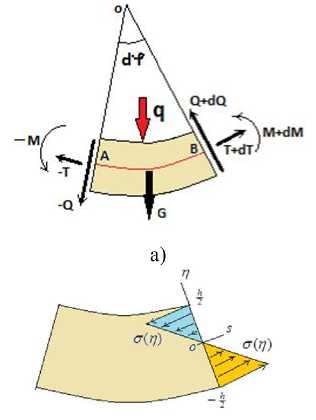
б)

Рисунок 2 - Схема напряженно-деформированного состояния балки: .а) – выделенный малый элемент балки с действующими на него силами, б) – распределение нормального напряжения в сечении s=const

Воспользуемся законом Гука, связывающим напряжения и деформации в локальной декартовой системе координат с базисом t, e y , n, учитывая, что в силу гипотезы плоских сечений, данные оси являются главными. Кроме того, единственной отличной от нуля деформацией будет деформация е_тт — е . Деформация по направлению у в силу наших предположений также равна нулю е_уу = 0. Используя малую толщину пластины, примем гипотезу о плоском напряжённом состоянии

стпи ~ 0. В результате получим Е Юнга, V — коэффициент Пуассона:

1 ^ett   ^E — O_TT

E = —

—

E 1

—

v² ^ TT ,

v

v

Ё°уу ^

^E nn

—модуль

^E yy = ⁰ = E ^a yy

—

E°TT ^

C yy — ^V^ TT , ^— p ⁽^ TT ⁺ O yy ) ^ ^E nn =

Фактически, закон Гука отношению:

E — —

—

Е

—

v(1+v) E °^TT,

сводится к со-

V2

;— ст, где CT — CTTT, (6)

Учитывая (2), (3), получим: Е

ct⁽s, т?) = y

—

^2E(s,T) = —

Е dp 1 — v2 ? ds,

Е ?

1 — V² R(s")

Наличие и асимметричный характер распределения действующих в сечении s=const напряжений а приводит к возникновению изгибающего момента M(s) при равной нулю равнодействующей силе:

M = —

J[r x от] dA

A

r = %(s, t)ex + z(s, t)ez,      (16)

dx⁽s, t)

—----= cos—(s, t), ds dy(s, t)

—----= sin—(s, t),  (17)

ds

Исключим в уравнениях (6) момент и спроектируем на оси (%, z):

так как:

r x т =

_  4aE

= (1 — v2)«

h

Jm²dm•e y

= dr

т

e,

e y = D^-e y ,  (8)

ds

= 0, dQ — cos — — ds

dQ             d— dx²

^— -sm^{— —Q}cos ^—- + ^u —+ d x

d—    dz2

Q sin—ds + U gt2" + ^у = 0,(19)

n

I т e y n| |o У m 11 0 0l

= me y

—

yn,

Q = Dd-—,M(s,t) = Dd—, ds2             ds

— = cos —(s, t), — = sin —(s, t). ds             ds

Ведём прогиб пластины

(21) w(s, t) =

n    a^h3

D = 6(1—v2)"

В выражении (5) D —

называется ци-

z(s, t). В случае малых углов поворота sin — « tg— « — и отсутствии внешних поверхностных сил q = 0 из (19) получим:

dw

линдрической жёсткостью пластины прямоугольной формы с шириной 2a и толщиной h относительно оси изгиба, параллельной у и проходящей через центр тяжести сечения. Помимо нормальных напряжений в сечении действуют и касательные напряжения, равнодействующую которых по сечению обозначим как Q(s) (рис. 2а). Эту силу в технических приложениях называют перерезывающей. Выпишем условия равновесия элемента, показанного на Рисунке 2а. Если оставаться в рамках гипотезы плоских сечений, то Q = Qn, где n — единичный вектор нормали к срединному волокну. Учитывая это, запишем условия равновесия сил и моментов:

d(Qn) + pahdsG + qds = 0, (10) dM + dsт x Qn + dsт x 2pahdsG

+ — т x dsq = 0, (11)

Если пренебречь массовыми силами тяжести, то в качестве массовых сил остаются силы инерции G = —r(s, t). После деления на длину ds и предельного перехода, получим (в согласии с (5), (1)) уравнения движения балки:

x « s, ф d4w

dx, d2w

ds      dt2

DTT+^7r = 0, dx4     dt2

d3w

d3w

Q = D —,M = D—, dx3         dx3

Балка скреплена пружиной

заданной

жёсткости k с телом массы m (Рисунок 3). Начальная длина пружины равна Ь ₀ , балка находится в горизонтальном недеформиро-ванном состоянии. В момент времени, который мы примем за начало отсчёта t = 0, масса имеет начальную скорость v_z = —У₀. Необходимо определить совместное движение механической системы: балка-пружина-тело, пренебрегая массой пружины.

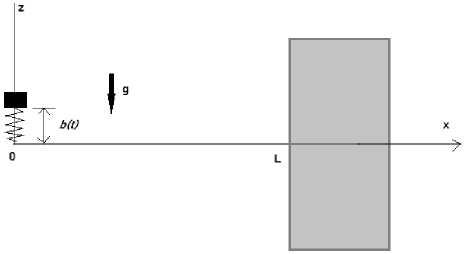
Рисунок 3 – Балка скреплена пружиной заданной жёсткости k с телом массы m

где u = 2pah; dM

ds

—

Q = 0, M(s, t) = D^d—, ds

так как:

т

e

n

т x n =

т  e y   n

10 0 =

^{— e} y ,

т = — = ex cos - (s, t) + ez sin —(s, t) ds n =—exsin—(s, t) + eycos—(s, t), (15)

Обозначим вертикальную координату тела как z(t). Учитывая прогиб балки, текущая длина пружины будет равна: d⁽t) = z⁽t) — W o ⁽t), где W o ⁽t) = w(%, t) i x=o ,5), что позволяет вычислить силу, которая растягивает (или сжимает) пружину F = k(b(t) — b o ) = k(z(t) — w(0, t) — b o ). (26)

Движение тела происходит под действием силы F, взятой с обратным знаком. Учитывая начальные условия, получим для

движения тела определяющие уравнения и

d2Z

—У + q2Z = q2w(0, t) — ^, dt2

со следующими начальными и

гранич-

начальные данные:

mz(t) = — k(z(t) — w(0, t) — b_o) — mg(10),

z(0) = b o , z(0) = —V o , w(0,0) = 0,     (28)

На левый край пластины % = 0 в момент времени t = 0 начинает действовать поперечная сила Q. Если сила F положительна,

ными условиями: t

= 0, w = 0, w =	0; Z = 0,Z = —r	;  (41)
d2w| x = 0,	= 0,^1   =f"	Z —f-
dx2 x =o	dx3 x=o
w(0,t);		(42)
	dw
x = 1,w| x=i =	°,d x=i = 0-	(43)

Как оказалось, задача (39), (41) зависит от следующих безразмерных параметров:

то есть пружина растягивается, то поперечная сила направлена вверх. Наоборот, кода пру-

жина сжимается, поперечная сила направлена

вниз. С учётом этого уравнения и условия для

p2

D

Eh2

^L2V02   12(1 — v2)pL2V02 ,q

пластины будут такими: 9⁴w    9²w

D^%4 + ^^t2 = t = 0, w = 0, w = 0;

92w x = 0,M = D    I ,Q

9x2

x=o

= k(z(t) — w(0, t)

0,0 < x < L; (29)

(30) 9²w ^{= D}d% 2 | x=o

_ kL2 mVo2

_ kL3

= ^”,

g      l

^ = LV o ^,r = h^,f

Будем решать задачу с использованием интегрального преобразования Лапласа [3, 7, 8] по времени:

— b o );                 (31)

x = L,w|_x=l = 0,^9W|   =0.     (32)

^9x x=L

u(t) ^образ

/ u(t) exp(—st) dt, i(s) ^оригинал d+i™

i(s) =

Результаты и обсуждение

Для удобства численных расчётов перейдём к безразмерным переменным (со знаком звёздочки):

x = Lx*, w = hw*, t = L/y t*, z = hz*, bo = hb0,             0   (33)

Общая система уравнений (27), (28)

примет вид:

h 9⁴w *     hV_o² 9²w *

^DL⁴5x^;4+^ L²  9t * ²

= 0,0 < x *

< 1,                   (34)

hV ) ² d²z *

mJ dt^ = —kh(z * — w * (0, t * ) — b 0 )

— mg,               (35)

t * = 0,w * = 0,w * = 0; z * = bo^z *

u(t) = -—-.  f  iz(s) exp(st) ds.   (46)

2rn d-i™

Применим к уравнениям (39) и условиям (40) преобразование Лапласа (45):

э       э 94?w s2w + p2 ——г = 0,0 < x < 1

9x4

s²T + r + q²T = q²iv(0, s) — ^ x =

92w9

0, I = 0, I

^9x2 _x =o      ^9x3 x=o

= f-Z — /-w(0,s);(47);

x = 1,w|x=i = 0,9W|    =0,(48)

^9x X=1

Второе уравнение позволяет исключить образ Z(s) и свести определение образа w(x, s) к следующей краевой задаче:

x * = 0,

9²w *

9x * ²

= —V o ;

h 93w*|

I^ 9x*3L

s²w + p²

x

= kh(z * — w * (0, t * )

— b 0 );                 (37)

9w *

x * = 1,w * |_x *= ₁ = 0,—|^__i = 0. (38)

Для удобства, введём замену функции Z * (t * ) = z * (t * ) — b 0 , и не будем писать знак звёздочки, понимая все переменные безразмерными. В результате получим следующую формулировку задачи – решить совместно си-

4:

q2

s2 + q2

—

—

f'P

s(s2 + q2);

x = 1,iv|_x =i

94w

— ^^x^, (49)

92w|

= 0, I

^9x2 L=o

1)-w(0,s) —

93w|

= 0,      |

^9x3 x=o

/ ■ r s2 + q2

=0,3

9x I

~

t; =

—

= 0.

X=1

r

—

стему уравнений:

92w   94w ip-^M^1 (39)

+

q

s2 + q2   s(s2 + q2)

s² + q²

w(0,s),  (52)

Решая дифференциальное уравнение находим:

w̃(x, s) = C 1 ∙ e^{nx(-s 2 ) 4} +C 2 ∙ e^{-nx(-s 2 ) 4}

+ C3 ∙ einx(-s2)4 + C4

∙ e -inx(-s²)⁴ ,

Где коэффициенты С1,С2,С3,С4 имеют следующий вид:

C1(s) = -1(f(rs+ β)(ie(1+i)n(-s2)4 -ie(-1+i)n(-s2)14 - 2 - e(1+i)n(-s2)14 - e(-1+i)n(-s2)4)/((4i(-s2)4n3q2 + ifs2e(-1-i)n(-s2)14 - ie(1+i)n(-s2)14fs2 + 31

i(-s 2 )₄n 3 s 2 e (-1+i)n(-s )⁴ +

i(-s 2 )₄n 3 s 2 e (1-i)n(-s )   +

i(-s2)4n3q2e(1+i)n(-s ) + ifs2e(-1+i)n(-s2)4 +

i(-s 2 )₄n 3 q 2 e (-1-i)n(-s )⁴ +

i(-s 2 )₄n 3 s 2 e (1+i)n(-s )   +

3 ¹ i(-s 2 )₄n 3 s 2 e (-1-i)n(-s ) +

i(-s 2 )₄n 3 q 2 e (-1+i)n(-s )⁴ +

i(-s 2 )₄n 3 q 2 e (1-i)n(-s )⁴ + 11

fs2e(-1+i)n(-s2)4 - fs2e(-1-i)n(-s2)4 + fs2e(1+i)n(-s2)4 - fs2e(1-i)n(-s2)4 +

4i(-s²) 4 n³s² - ie^{(1-i)n(-s 2 ) 4} fs²) s);  (54)

C2(s) = 1(f(rs+ β)(ie(1-i)n(-s2)14 + 2i+ ie(1+i)n(-s2)14 + e(1-i)n(-s2)14 - e(1+i)n(-s2)4)/((4i(-s2)4n3q2 + ifs2e(-1-i)n(-s2)14 - ie(1+i)n(-s2)14fs2 + 31

i(-s 2 )₄n 3 s 2 e (-1+i)n(-s ) +

i(-s 2 )₄n 3 s 2 e (1-i)n(-s )   +

i(-s2)4n3q2e(1+i)n(-s )4 + ifs2e(-1+i)n(-s2)4 +

i(-s2)4n3q2e(-1-i)n(-s )

i(-s2)4n3s2e(1+i)n(-s )

i(-s 2 )₄n 3 s 2 e (-1-i)n(-s )⁴ +

i(-s2)4n3q2e(1-i)n(-s )

fs2e(-1+i)n(-s2)4 - fs2e(-1-i)n(-s2)4 + fs2e(1+i)n(-s2)4 - fs2e(1-i)n(-s2)4 +

4i(-s²) 4 n³s² - ie^{(1-i)n(-s 2 ) 4} fs²) s);

C 3 (s) = ¹ (f(rs+ β)(ie^{(1-i)n(-s 2 ) 4} - _ie(-1-i)n(-s²) ¹ 4 _{+ 2 + e}(1-i)n(-s²) ¹ 4 ₊

e(-1-i)n(-s2)4)/((4i(-s2)4n3q2 + ifs2e(-1-i)n(-s2)14 - ie(1+i)n(-s2)14fs2 +

i(-s 2 )₄n 3 s 2 e (-1+i)n(-s )⁴ +

i(-s 2 )₄n 3 s 2 e (1-i)n(-s ) +

i(-s2)4n3q2e(1+i)n(-s ) + ifs2e(-1+i)n(-s2)4 +

i(-s 2 )₄n 3 q 2 e (-1-i)n(-s )⁴ +

i(-s 2 )₄n 3 s 2 e (1+i)n(-s ) +

i(-s 2 )₄n 3 s 2 e (-1-i)n(-s ) +

i(-s 2 )₄n 3 q 2 e (-1+i)n(-s )⁴ +

i(-s2)4n3q2e(1-i)n(-s )4 + fs2e(-1+i)n(-s2)14 - fs2e(-1-i)n(-s2)14 + fs2e(1+i)n(-s2)4 - fs2e(1-i)n(-s2)4 +

4i(-s²) ⁴ n³s² - ie^{(1-i)n(-s 2 ) 4} fs²) s);

C 4 (s) = - ¹ (f(rs+ β)(ie^{(-1-i)n(-s 2 ) 4} + _ie(-1+i)n(-s²) ¹ 4 _+2i-e(-1-i)n(-s²) ¹ 4₊

e(-1+i)n(-s2)4)/((4i(-s2)4n3q2 + ifs2e(-1-i)n(-s2)14 - ie(1+i)n(-s2)14fs2 +

i(-s 2 )₄n 3 s 2 e (-1+i)n(-s )⁴ +

i(-s 2 )₄n 3 s 2 e (1-i)n(-s )⁴ +

i(-s2)4n3q2e(1+i)n(-s )

ifs2e(-1+i)n(-s2)4 +

i(-s2)4n3q2e(-1-i)n(-s )

i(-s 2 )₄n 3 s 2 e (1+i)n(-s )⁴ +

i(-s2)4n3s2e(-1-i)n(-s )

i(-s2)4n3q2e(-1+i)n(-s )

3                      1

i(—s²) 4 n³q²e^{(1-i)n(-s )4} + _fs2 e (-1+i)n(-s²)⁴ - _fs2_e(-1-i)n(-s²)⁴ + _fs2 e (1+i)n(-s²)⁴ - _fs2_e(i-i)n(-s²)⁴ +

4i(-s²) 4 n³s² — ie^{(1 i)n(} s^{2 ) 4} fs²)s);

Простым вычислением и подстановкой находим функцию координаты тела:

л ^q2(^ i ^{+ £} 2 ^{+ £} 3 ⁺ £ 4 )

^z(s)=----q 2TP-----

-

r

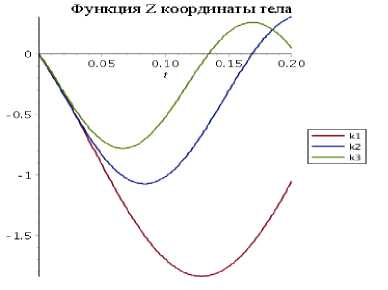
Функция "W прогиба балки

a)

s(q2 + s2)

-

q² + s^{2 ;}

Возьмем следующие значения для па- раметров:

p = 500^,E = 2,0 • 10¹⁰na,v = 0,3, a = 0,5 м, h = 0,1 м, L = 1,5 м, V₀ = 1 м/с, k =

• ¹⁰ 4 ^H/ _M ,m = 70 кг.         (59)

Используя метод Дурбина находим оригиналы функций прогиба и координаты тела (Рисунок 4 a-b):

Проверим зависимость функций прогиба балки и координаты тела от параметров жесткости пружины и размера балки:

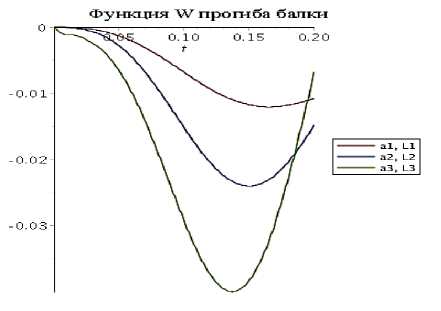
• а)    жесткость пружины (Рисунок 5 a-b):

k₁ = 10 4 Н/м,к₂ = 2 • 10⁴Н/м,к₃ =

3 • 104Н/м                 (60)

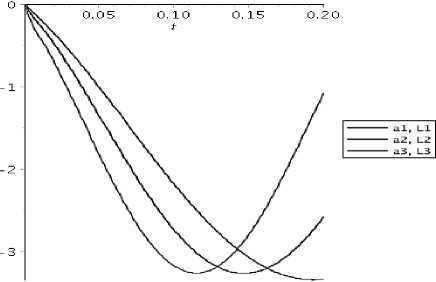
• б)    размер балки (Рисунок 6 a-b):

a1 = 0,5 м, a2 = 0,7 м, a3 = 0,9 м, L1 =

• 1,5 м, L 2 = 2 м, L₃ = 2,5 м,         (61)

  

  б)

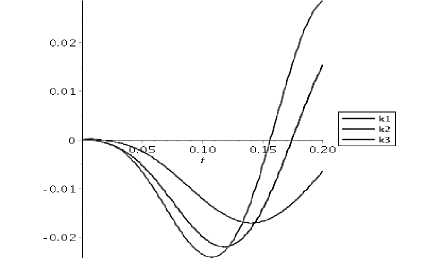
  Рисунок 5 – Зависимость функций прогиба балки и координаты тела от параметров жесткости пружины

  
  
  

  a)

  
  

  Функция W прогиба балки

  
  
  

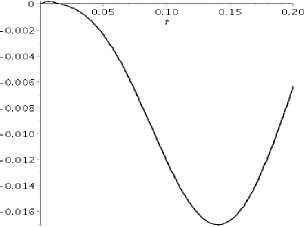
  a)

  

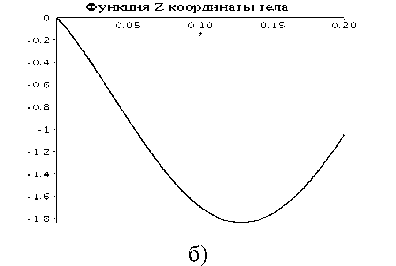
  Рисунок 4 – Оригиналы функций прогиба и

  координаты тела

  
  

  Функция Z координаты тела

  

  б)

  Рисунок 6 – Зависимость функций прогиба балки и координаты тела от размера балки

  
  

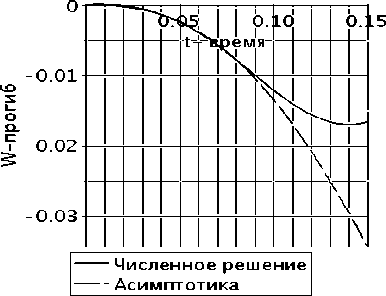
Сравнение аналитического и численного метода Дурбина [5, 9, 10]. Покажем, что аналитическое и численное решение обратного преобразования Лапласа [3] методом Дурбина [5] на малых промежутках времени совпадают (Рисунок 7 a-b).

Сравнение численного и асимптотического (для малых значений времени) решений

a)

Движение груза. Сравнение числ. и аснмпт (для малых значений времени) решений

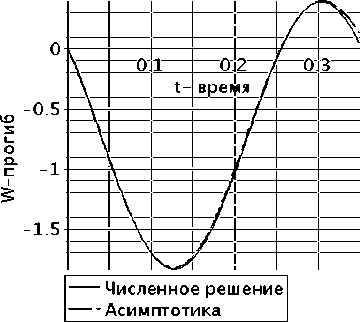
б)

Рисунок 7 – Сравнение аналитического и численного метода Дурбина

Выводы

С помощью условия равновесия сил и моментов построена система уравнений решения задачи нагружения балки пружиной с закрепленной массой. Использовав прямое преобразования Лапласа система уравнений была значительно упрощена. Решив дифференциальное уравнение был найден образ функции прогиба, а постановкой – образ функции движения тела. Численный метод Дурбина обращения интегрального преобразования Лапласа в данной задаче является применимым.

Метод дает результаты, на начальном малом участке времени совпадающие с анали- тическим решением. Подстановкой конкретных чисел в параметры решений были построены графики функции прогиба и функции координаты тела от времени.

Для сравнения зависимости функций от параметров жесткости пружины и размера балки были построены графики этих функций от данных параметров при различных их значениях. Было выяснено, что при увеличении жесткости пружины значения функции прогиба и функции координаты тела также увеличиваются. А при увеличении жесткости балки значения функции прогиба и функции координаты тела уменьшаются. Этот результат полностью отражает практическую постановку.