Динамика полишарнирных механических систем

Поляков Алексей Афанасьевич Екатеринбург, зав. каф. стр. механики УГТУ-УПИ, д.т.н., профессор

Поляков Артем Алексеевич Екатеринбург, зам. главного конструктора по новой технике ЗАСГУромгаз”, к.т.н.

Двухшарнирные и полишарнирные механические передачи и состоящие из них системы нашли широкое применение в различных отраслях промышленности таких как транспортная, нефтегазовая, металургическая и т.д. При этом, шарнирные системы могут быть плоскими (оси валов, связанные с шарнирами, находятся в одной плоскости) и пространственными [1, 3, 5].

Исследование динамики плоских шарнирных систем при определенных ограничениях рассматривалась в работах [1-3], где показано, что в таких системах возникают вынужденные колебания, неустойчивые движения и различные резонансы.

Например, в приводах исполнительного органа очистных машин [1-3] используются пространственные, шарнирные, механические системы. Динамические процессы, происходящие в них, имеют более сложный характер, так как системы с пространственными шарнирами позволяют передавать нагрузки и вращение между валами с пересекающимися осями в широком диапазоне статических и динамических параметров.

Характерной особенностью механических шарнирных систем является наличие в них пространственных шарниров, вызывающих неравномерность вращения звеньев и связанные с ними колебания [2, 3]. Колебания возникают даже тогда, когда внешние моменты, приложенные к ведущим и ведомым звеньям, постоянны.

Таким образом, сама механическая шарнирная система является источником крутильных колебаний, неравномерности вращения звеньев, и в сочетании с другими источниками колебаний (ведущим и исполнительным органами) могут приводить к значительным динамическим нагрузкам как в самом приводе, так и на его выходе, а также к вибрациям оборудования и конструкций.

Рассматривается динамика полишарнир-ных механических систем. Приводится обобщенная динамическая модель, которая учитывает влияние на динамический процесс кинематики универсальных шарниров, углов перекоса осей валов, упруго-вязкого демпфирования. Приведены: математическая модель, описываемая системой нелинейных дифференциальных уравнений; результаты расчетов динамических нагрузок и коэффициентов; зоны различных видов резонансов; критерии оптимизации по снижению динамических нагрузок в данных системах.

При определённых соотношениях статических и динамических параметров в приводе с пространственными шарнирами могут возникнуть неустойчивые состояния, сопровождающиеся повышением уровней упругих колебаний, параметрические колебания и параметрический резонанс, оказывающие существенное влияние на нормальный режим работы оборудования и эксплуатационную надёжность. Поэтому исследование динамических явлений необходимо для установления рациональных режимов и создания, в конечном итоге, надёжной и экономичной техники.

В рассматриваемой работе приводятся исследования динамики привода рабочего органа, представляющего собой разветвленную многосвязанную систему с пространственными шарнирами [2-4].

Характерная такой системе динамическая модель представлена на рис. 1, которая учитывает влияние на динамический процесс всех основных факторов: кинематической особенности шарниров, статических и динамических параметров системы.

Динамическая модель описывается системой нелинейных дифференциальных уравнений, полученной на основе использовании квазистатического способа, при непосредственном применении принципа Даламбера.

После преобразования данной системы к виду удобному для компьютерной реализации с помощью численного метода интегрирования Рунге-Кутта, уравнения системы имеют вид:

---”^2/ ^1,2W         (О

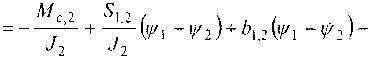
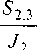
(^2 -Уз)Лзк -^з);

^--у^ + у^^-^зЬбз.г^г-^з)-

—^-(^3 -УзУЬз^з"УзУ

• •    -^-(^3-^7)-63,7 (^3-^7);

• •    ■     МС Д   Sy ,        X S7 J3 zх

Vi =——+— ^+-y-(^7 ~^13/“

Лдз^ -^+hAv3 -1/7);

S1 13•

13 ~~ 1/7,13 + ^7,13^7,13 “

^S\3,W (       . V ^MTp,I ,

• -yu)Fx - —;

■ ■       ^13,14 (           * ) , Д *      ■)

1/14 =-y—Г13 ~^14 J" *14,15^14 — 1/15/ /14

C /x

°14,15 / *

• 7— Г14 ~1Z15 Л

■ ■        ^14,15 ( *           \ ,       ( ■ • . )

1/15 ~  ; У 14 ~ 1/15/+615,14 у 14 ”1/15/

^15,16 (        «        ^ Tp Л

J15                     J15

1/16 =у^(/15 * 1/16 )" ^16,8 (/16 ”l/s‘)” /16

^16,8 ( •       )

У 16 "^вД

J16

1/8 =~ 7~ ^16 -1/8 /+ "8

+^8,16 У16 -1/8

1/9 =y^(l/5 -I/9) + \5(l/5 -I/9)-

^9,10

(      * \ MTpX

I1/9-1/10 Л-- 1 ’

$12,6 / *

--— Г12 "l/б

J12

1/б =—11/12 -1/бу612б11/12 -^бУ—Т-

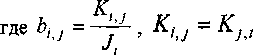
В уравнениях (2) точкой обозначено дифференцирование по времени t. При этом параметры, входящие в эти уравнения обозначают: у* - уг лы поворота z-й массы, имеющие явную кинематическую связь с углами поворота (z-1) массы [рад]; К^ - коэффициенты пропорциональности между величиной потерь внутреннего трения в упругой связи, выраженной в размерности момента, и величиной относительной скорости перемещения масс [Н-м-с]; Мд - момент на двигателе [Н м ]; Mc-i- момент вязкого трения в элементах 1-й массы [Н-м]; М^д- момент трения в z - ом пространственном шарнире [Н-м]; Мт3 - технологический момент, приложенный к z-й массе [Н-м]; Jj - момент инерции z-го элемента системы [Н-м-с2]; Sy - жесткось i,j-ro вала [Н-м/рад]; F, -кинематические функции.

Кинематические функции (F^, входящие в уравнения (1), зависят от типа механической шарнирной передачи и ее параметров.

Так, для одной из линий привода рабочего органа (выделенной на рис. 1 пунктирным прямоугольником) механическая шарнирная передача включает три звена (5,13; 14,15; 16,6), связанных между собой двумя универсальными шарнирами. Подробно фрагмент этой передачи приведен на рис. 2. Применительно к выделенному фрагменту (рис. 2) кинематические функции F_x и F₂ соответствуют случаю, когда оси всех валов расположены в разных плоскостях (у, * 0, у₂ * 0, Pt * 0, р₂ * 0), имеют аналогичный вид, в частности для F_x;

созД cossin² Д sin² у_х

F ----------------------------’

Г где г = cos2 /] +(sin2 /х - sin2 Д )sin2 р13 +

1^10 -~7~V9 -1/10/-^10,11 /10

C /            X

7 у 10 ~Уп)>

]! - . ,   У10 -1/ц /+610,liyi0 “1/ц,

/11

$11,12 /       * У ^Тр,3

/п             /ц

„      ^11,12

1/12 =-T-/12

+0,25 sin 2у_х sin 2Д sin 2^₁₃.

Исследовано влияние на динамические на грузки углов перекоса шарниров, приведенных моментов инерции, угловых скоростей, жесткостей звеньев, технологических моментов. Для примера приведен график рис. 3.

Определены динамические коэффициенты и установлены зоны резонансов для различного сочетания параметров системы в качестве примера на рис. 4. приведен график изменения динамических коэффициентов на котором четко наблюдаются как основные так дробные резонансы.

Теоретические исследования

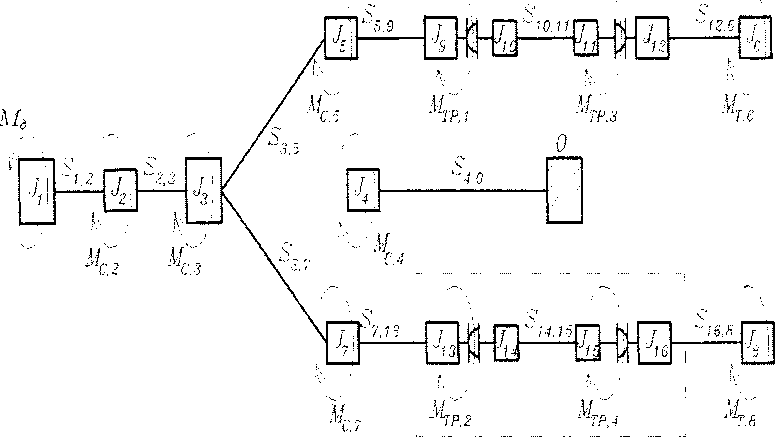
Рис. 1. Динамическая модель рабочего органа

М_а - момент на двигателе, J, - момент инерции /-го элемента системы, S_y - жесткось /", у-го вала, М_с, - момент вязкого трения в элементах i-й массы, M_Tp,i - момент трения в i-м пространственном шарнире, М_т,1 - технологический момент, приложенный к /-й массе

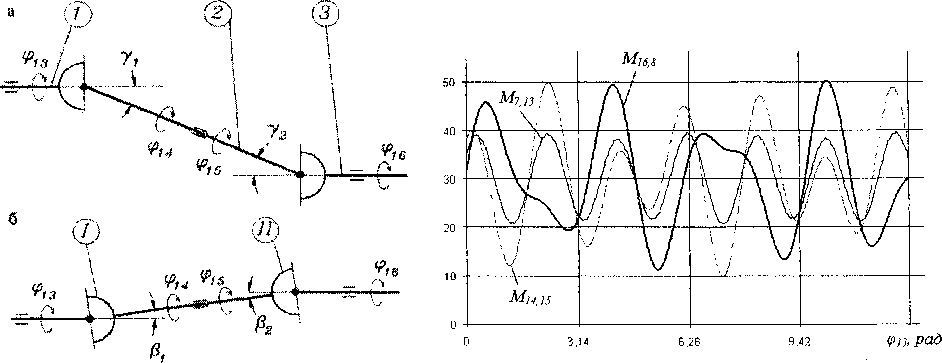
Рис. 2. Пространственная двухшарнирная передача (фрагмент из рис. 1):

а - вид фронтальной проекции, 1- ведущий вал, 2 -промежуточный вал, 3 - ведомый вал; б - вид передачи в плане; l,ll - универсальные шарниры,

Yi, Y2, ₽i, Р2 - углы между геометрическими осями (углы перекоса), соответственно 1-го и 2-го, 2-го и 3-го валов

Решена задача поиска рационального угла относительного расположения двухшарнирных передач, входящих в разветвленную систему рабочего привода, обеспечивающего минимальные динамические нагрузки в системе [4]. При этом, для оценки неравномерности нагрузок использованы два критерия неравномерности момента передаваемого на вал двигателя:

• 1.    Критерий К\ - среднее значение за период модуля разности моментов на ведущих звеньях передач:

• 2.    Критерий К_г - максимальное значение разности моментов на ведущих звеньях:

K_x=-\^\M_S1-M_T\dt,         (3)

f о-=1'

Рис. 3. Изменение динамических моментов в звеньях шарнирной передачи в зависимости от угла поворота ф13 ведущего звена при о>=30 с"1 : М7|13 - ведущего; MM,i6 - промежуточного; Mi6,s - ведомого где i = 1,2,...т зависит от количества шарнирных передач, входящих в систему привода, Ms., -суммарный момент, передаваемый на звенья двигателя от всех шарнирных передач.

П1

1=1

На рис. 5 представлены некоторые результаты расчета, в частности, графики распределения К_х и ЛЗ от угла а относительного расположения шарнирных передач.

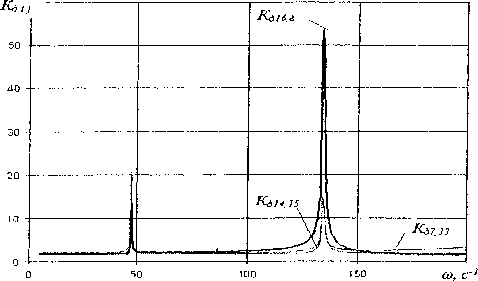
Рис. 4. Изменение динамических коэффициентов K_aij=f(w) в звеньях шарнирной передачи от угловой скорости ш: Кд7,1₃ ,К_Я14,16, /(gie.s - ведущего, промежуточного, ведомого звеньев, соответственно

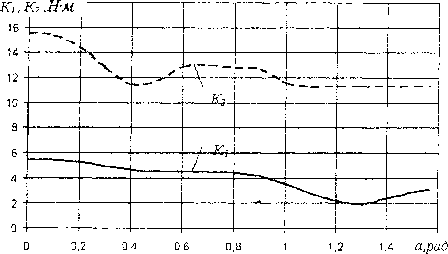
Рис.5. Графическая зависимость критериев Ki=f(a) и K₂=f(a) при ш=70 с^-1 от угла а относительного расположения шарнирных передач

Минимуму первого критерия соответствует угол а6 при котором среднее значение модуля разности моментов за время / -минимально.

Минимуму второго критерия соответствует угол а„ при котором максимальное значение модуля разности моментов - минимально.

Анализ результатов динамических нагрузок и влияния различных факторов на поведение динамической системы показал что существует возможность для рекомендации по выбору параметров системы, при которых динамические нагрузки имеют минимальные значения и исключается риск возникновения резонансов в системе