Динамика потока в радиально-кольцевой полости турбомашин

Введение. Турбомашины различного типа (насосы, компрессоры, турбины, детандеры) в настоящее время применяются повсеместно. В процессе проектирования и конструирования турбомашин зачастую возникают вопросы корректного моделирования движения потока жидкости или газа в рабочих полостях для оценки полей распределения скорости и давления, напряжений трения, коэффициентов потерь и общей энергетической эффективности турбомашины [1-4]. Задача моделирования осложняется тем, что течение носит сложный пространственный характер [5-6], для учета которого целесообразно разложение основной системы уравнений на две проекции - радиальную и окружную. Итоговый вид системы уравнений движения зависит от конструкции полости турбомашины [7].

В рамках настоящей работы рассматривается задача моделирования вращательного течения в радиально-кольцевой полости турбомашины с неподвижными стенками, что соответствует граничным условиям подводящего канала для радиальной центростремительной турбины. Представленный в работе подход может быть использован для расчета турбин других типов.

Постановка задачи исследования. Основная задача работы - для расчетного случая течения в подводящем устройстве радиальной центростремительной турбины необходимо получить систему уравнений, корректно описывающих поля распределения давления и скорости на входе в рабочее колесо. При этом необходимо учитывать следующую специфику [8-11]:

• -    корректное формирование (без потерь) полей скорости и давлений перед рабочим колесом в основном определяет величину окружной мощности турбины, и, как следствие, общий КПД турбины.

• -    парциальность, неравномерность полей скорости и давления в данной области определяют величину осевой нагрузки на ротор турбины, что снижает ресурс узлов качения [12].

Для решения поставленной задачи необходимо преобразовать уравнения движения совместно с уравнением неразрывности с целью получить выражения для численного интегрирования для расходной и окружной составляющей скорости, а также статического давления, учитывающие массовый расход как исходный параметр.

Основные допущения и расчетная схема течения. Радиально-кольцевые полости турбомашин при разнонаправленных течениях относительно радиуса R могут формировать конфузорное или диффузорное течение. Данное течение осесимметрично, поэтому решение рассматривается в цилиндрических координатах с условием ∂/∂x=0.

Возможны два случая течения: чисто радиальное C=V R и радиально-окружное C=(V R ²+U²)^0,5 . В обоих случаях для анализа используется уравнение сохранения количества движения для массового потока жидкости. Расчетная схема радиально-кольцевой полости представлена на рис. 1.

Площадь проходного сечения в радиальном направлении F R определяется выражением:

F r = 2n R • n oz , (1)

где R – радиус полости, n 0z – осевой зазор в направлении координаты z.

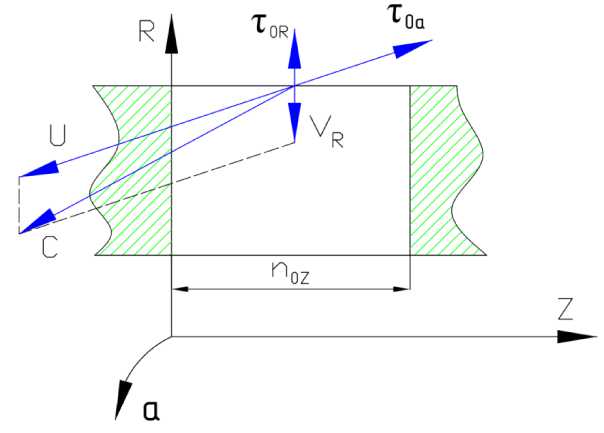
Рис. 1. Расчетная схема радиально-кольцевой полости

R, Z, а – координаты; C, U, V R – компоненты скорости; τ 0R , τ 0a – напряжения трения в радиальном и окружном направлении; n 0z – нормальный зазор

Fig. 1. Calculation scheme of a radial-annular cavity

R, Z, a – coordinates; C, U, V R – velocity components; τ 0R , τ 0a – friction stresses in the radial and circumferential direction; n 0z – normal clearance

Приращение площади проходного сечения в радиальном направлении:

dF_z = 2n R • dR .

Выражения (1) и (2) определяют геометрические параметры проходного сечения на шаге интегрирования, позволяющие найти радиальную скорость при известном массовом расходе рабочего тела.

Математическая модель течения. Приращение изменения количества движения для потока в дифференциальной форме определяется выражением:

dV m—R • dR

dR

d ( P • Fr ) dR

• dR + 2 dF_z t_r ,

где ṁ – массовый расход; V R – радиальная составляющая скорости; τ 0R – окружная составляющая напряжения трения на стенке, p – величина давления.

С учетом (1) выражение для радиальной составляющей скорости имеет вид:

mm -------=------------. Р • FR  P • Mnoz

Преобразуем уравнение (3) с учетом (2):

dV     dp dF m —R = Fr — + p —R + t „ • 4nRdR. dR R dR    dR oR

Определим производную радиальной составляющей скорости, используя уравнение (4):

dVR _ d f   m   ^ _   -m dR dR ( p • 2nRnoz J p • 2nR2noz ’ dV   V ds=-1'

Производная площади проходного сечения F R с учетом (1) определяется по выражению:

dFR- = — (2n• Rn z) = 2nn z. dR dR        oz        oz

Принимая во внимание (6) и (7), перепишем выражение (5) в виде:

- mv_R  — dp _

----R = F_r --+ 2 n n_n7 • p + т _R R              oz        oR

R     dR

• 4 n R .

Выделим в этом выражении производную dp/dR :

	dp _ - m  2 n no^    4 nR =                • p        • Tp.                                (8) dR  F R   F      F   0 R
Учитывая (1) и (4), получим:	dp = _ EVL _ p _ 2 £ o R . . .                          (9) dR     R   R   n    oR ,
или окончательно	• dp =---- m ^ - p - 2 T 0R- ,                  (10) dR   p • 4 n 2 • n0 :z • R 3    R    noz

Напомним, что при течении к центру координат ( -V R ) течение конфузорное и наоборот.

Для радиального потока достаточно системы уравнений (4) и (9), причем V R = const. Для радиального потока с окружной составляющей необходимо соотношение для окружной скорости U . Для потенциального течения rot U = 0 , выполняется соотношение:

U • R = C_u = const .

Соотношение (11) вполне определяет функцию U=f(R) , однако при интегрировании по радиусу необходимо учитывать влияние окружной составляющей напряжения трения на стенке т оа , которое при любом направлении радиальной скорости Vr снижает значения С и [13].

Найдем далее соотношения для окружной составляющей скорости радиально -окружного потока. Используем закон изменения момента количества движения [14-15]:

m d ^(U • ^R ) • dR = dF_m ■ R ,                              (12)

dR            тр , где dFmp - сила трения на элементарном объеме 2nno.-dR.

Сила трения по двум поверхностям (см. рис. 1):

dF mp = 4 T oa • n R • dR ,

Возьмем производную от выражения (12) и учтем (13):

dU U 4пт

+Oa

— dR   Rm

m R--+ U = 4Rт • 4nR.

I dR )        ^oa

Выразим производную:

dU U 4лт_па R +     Oa

— dR   R   m

Или с учетом U=^R , получим выражение:

dm 2m 4пт dR - R+.

С учетом (11) окончательно получим:

dCu   4nR2тоа = 2Rtoq dR      m      no. ' P • VR

Выражения (14), (15), (16) можно интегрировать автономно без знаний об изменении поля давления p .

Далее найдем соотношения для статического давления для радиально-окружного потока. Используем уравнение изменения количества движения для абсолютной скорости (см. рис. 1):

с=4 v R2 + u ²,

где и U определяется по выражениям (4) и (11). После преобразований получим:

m — • dR = ^{d (} p " F^R ) • dR + 2т _R • dF , dR          dR            ^{oR z ,}

где dF z =4πRdR – двойная боковая поверхность элементарного объема dV=2πRn 0z ·dR

F R =2πRn 0z – площадь проходного сечения.

Определим производные скоростей. Производная dV R /dR , согласно выражению (6):

dV    V

R R

.

dR    R

Производная окружной составляющей с учетом выражения (11) на элементарном объеме dV=2πRn 0z ·dR может быть определена в виде:

dU   C dR     R2 .

Производная dC/dR согласно выражению (17) определится как:

dC d(,      05   1/ ,    ,4-0.5  d 7 ,    ,40.5   1/ ,    ,4-0.5 ( dV„dU \

22   22    22   22

---—     Vp + U    — Vn + U     • Vp + U    — Vp + U     • 2V p--+ 2U.

dR dR^V*     ’    2^V R      ¹ dR^{V R}      '    2^{V R      }} I ^R dR      dR J

Учтем выражения (19) и (20) и продолжим преобразование:

dC — 1 ( V 2 + U ² )"°'⁵ • (- 2V_R d^ - 2UdU ) , dR 2^V R      ’   ( R dR      dR J

dC dR

-    /(V2 + U²)

RR

C

. R

C учетом (21) преобразуем выражение (18) к виду:

Cm R

dp   dF_R

— F_r --+ p --+ 2 т _R • dF .

R dR    dR     oR z

После подстановки выражений (1) и (2) получим соответственно:

R — 2 nn _z;   2 dF — 4 n RdR ;   F_R — 2n Rn_{n z};

oz          z                     R            oz тогда

---dR — I F_Rdp + pF R I dR + 4 т _R • n • R • dR . R      ( ^R dR    R J       o ^R

Сократим последнее выражение на dR , в результате получим:

- mC     dp F

=F +p R+4⋅π⋅R⋅τ.

R     R dR    R          oR

Выразим производную по давлению:

dp      m      1   4 ⋅π⋅ R ⋅τ dR = RF p R + F учтем VR= ṁ/ρFR, получаем:

dp      m ⋅ C p 2 ⋅ τ

=-      -  - dR    2πR2noz  R   noz

Выражение (25) совместно с выражениями (4) и (17) образуют замкнутую систему уравнений для определения полей скоростей и давления в радиально-кольцевой полости турбомашин.

Заключение. Полученная в работе математическая модель может быть использована при комплексном моделировании радиальных центростремительных турбомашин для расчета динамики потока в подводящих и отводящих устройствах. Модель определяет поля скоростей и давления на входе и выходе ротора, что в свою очередь является условием, формирующим вектор радиальных и осевых сил, определяющих динамику ротора, нагрузку на узлы качения, и, как следствие ресурс турбомашины в целом. Представленный в работе подход может быть использован для расчета турбин других типов.