Динамика пространственного движения роторной системы в задачах динамической диагностики

Введение. При построении систем динамической диагностики узлов трения в роторных системах типичной задачей является выяснение взаимосвязи изменяющейся геометрии контактирующих поверхностей с наблюдаемыми координатами. Для этого, прежде всего, необходимо создать математическую модель динамики диагностируемого объекта. Рассмотрим методику построения модели роторной системы.

В большинстве случаев роторные системы представляют собой тела (валы), имеющие две различные точки закрепления в подшипниках. Для математического описания роторной системы, совершающей пространственное движение, необходимо задать две системы дифференциальных уравнений: систему, определяющую динамику движения центра масс, а также динамику сферического движения.

Уравнение Эйлера в параметрах Родрига–Гамильтона. Обозначим неподвижную прямоугольную систему координат как X = [ Х 1 х₂ Х 3 ] , где Д - орты соответствующих осей (рис. 1). Кроме того, свяжем с валом подвижную прямоугольную систему координат Y = [ у 1 у 2 у₃ ] , где уj - орты соответствующих осей. Причем, выберем Y так, чтобы начало системы координат совпадало с центром масс вала c , а оси совпадали с главными осями инерции вала в точке c . Тогда, в соответствии с теоремой о движении центра масс [1], первая система уравнений примет вид:

mс X = F , i = й ,                                 (1)

где   сiX – координаты точки c (центра масс) в X ; FiX – проекции главного вектора внешних сил F на оси в X ; m – масса вала.

Рис. 1. Обобщенная роторная система

Вторая система дифференциальных уравнений, определяющая сферическое движение твердого тела, как известно, описывается уравнениями Эйлера [1]:

J 1 ^m Г + ® Г ^m 2 ( J 3 - J 2 ) = M Y ,

* J 2 ^m 2 ^+Ю Г ^m Y ^{( J} 1 - J 3 ^{)= M} Y ,                                      ⁽²⁾

j3m 3+m Y mY ( j2 - j1 )=mY, где  Mi, mY - проекции соответственно главного вектора внешних моментов M и угловой час- тоты на оси Y ; Ji – моменты инерции.

Очевидным недостатком уравнений (2) является то, что они представлены в подвижной системе координат. Кроме того, из них явным образом не следуют динамика положения вала, так как m Y задает лишь его «скорость изменения». Для устранения последнего недостатка необходимо задать способ представления вала в пространстве, т. е. такую систему переменных, которая бы однозначным образом определяла ориентацию вала, и выразить m Y через данную совокупность переменных. Существуют различные способы решения данной проблемы. В качестве таких переменных нами использованы так называемые параметры Родрига–Гамильтона.

В соответствии с теоремой Эйлера–Даламбера, абсолютно твердое тело из произвольного начального положения может быть переведено в любое другое положение (при сферическом движении) посредством лишь одного конечного поворота вокруг некоторой оси O ^ на угол ф . Это свойство положено в основу кватернионной кинематики сферического движения твердого тела [2]. Исходя из нее любое положение твердого тела (относительно некоторого начального) 3

может быть описано посредством кватерниона Л = Х _о + ^ i i X i , где X i - параметры Родрига- i =1

Гамильтона, i _i – кватернионные единицы. Кватернионные единицы могут быть ассоциированы с ортами x , х₂ , Х ₃ , т. е. будет иметь место x = i i . При этом говорят, что кватернион представлен в базисе X . В дальнейшем рассмотрены лишь кватернионы в X . В кватернионной кинематике на параметры Родрига–Гамильтона налагают условие нормировки:

х _о ² +х 2 +х 2 +х 2 = 1 .                                   (3)

Для любого вектора V , представленного координатами V_X в неподвижном базисе X , можно найти его координатное представление в базисе Y по формуле:

V i = PV ,                                         (4)

где P – матрица направляющих косинусов, определенная как

2 ( Х , Х 2 +X o X ₃ ) 2 ( Х , Х з -Х о Х з ) " Х _о ² - Х 2 + X 2 - Х 3 2 ( Х ₂ Х ₃ + X _о х , ) .

2 ( х ₂ х ₃ -хд ) х о -х 2 -х 2 +х ₃ ²

Х _о ² +Х^

-

х

-

х

P = 2 ( Х,Х ₂

-

Х о Х ₃ )

2 ( Х,Х ₃ +Х _о Х ₂ )

Установим связь между проекциями вектора угловой частоты m на подвижные оси Y и параметрами Родрига–Гамильтона. Для этого используем кинематическое уравнение Пуассона:

• 1

Л = -Л о m ,                                    (5)

где символ « о » обозначает операцию кватернионного умножения.

Используя матричное представление кватернионов [2], можно получить координатную запись данного выражения:

'm Y = 2 ( х о; Х , -х , Х о -х 2 Х 3	+ Х3>Х 2 ) ,
m Y = 2 ( хо;Х 2 -х 2 X о +х,;Х 3	-Х 3 Х , ) ,                                      (6)
m i = 2 ( х о; Х 3 -х , Х 2 +х 2 Х ,	-Х 3 Х о ) .

Подставив уравнения (6) в уравнения динамики сферического движения (2), получим систему уравнений динамики сферического движения в параметрах Родрига–Гамильтона. Причем условие нормировки (3) необходимо рассматривать в качестве одного из первых интегралов движения. Однако полученная система имеет неудобную форму для проведения численного моделирования. Получим более компактную форму. Из формулы (6), а также из условия нормировки, несложно видеть, что имеет место:

/г

•

Y

Y

Y у :

Ю 3 Ю-

Ю , Ю

^Ю 2 ^Ю,

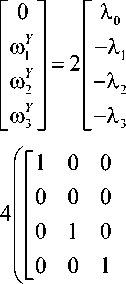
Х 1

X 0

-Х з

Х 2

Х 2

Хз

Х о

■ X1

Х _з

^-Х 2

Х 1

Х о

Х о

-Х ₁

-Х ₂

Х о

Х 1

Х 2

-Х ₁

-Х ₂

-Х _з

Х 1

Х о

^—Х з

Х о

Х з

-Х _з

Х 2

Х 2

Х 3

Х о

Х о

-Х ₁

•

Х о

•

Х ,

•

Х 2

•

.Х з j

Х ₃

^-Х 2

Х 1

,

Х 3

-Х 2

Х 1

Х о

•

х,

([ о

-Х ₃

Х 2

-Х ₁

Х о

•

Х о

1\

•

Х 1

•

Х ₂

•

•

X , з jy

1\

•

Х 1

•

Х 2

•

,

. ^Хз jy

где под символом « • » подразумевается операция поэлементного умножения.

Операция поэлементного умножения определяется следующим образом: если A = [ a ij j и

B = [ b ij j , то матрица, определенная как C = A • B , будет состоять из элементов c ij = a ij b ij .

Продифференцировав (7), с учетом (3) получим: ■ о" ■ Хо Х1 Х2 Хз 1 г •• и Хо • Y Ю1 Ю Y =2 -Х1 -Х2 Хо -Х3 Х3 Хо -Х2 Х1 ••1 Х 2 - M о, (9) .О 33 _ _-Хз Х2 -Х1 Хо j _Хз _ где M0 – вспомогательное обозначение, определяемое следующим образом:

м 0 = [- 2 ( Х 0 + Х 2 + Х 2 + Х 3 ) о о o j ^т .

Введем следующие обозначения:

■Х о "

■ Х о

Х 1

Х 2     Х з

1

■ о

о о 1

Х

—

Х 1 Х 2

, Л

—

-Х 1 -Х 2

Х о -Х з

Х з -Х 2 Х о     Х 1

,

K =

1 о

00 10

,

.

Х з j

.-Х з

Х 2

Х 1     Х о

j

. о

о 1 j

■ 1

0

0

о "

■ 1

0

0

о "

■

1

0

0

о 1

T =

о о

0 1

0 0

1 0

, J

= 2

о о

J 1 0

0 J 2

0 0

, G = 4

о о

J 3

- J 2 0

0 J 1 -

J 3

о о

. о

0

1

о .

. о

0

0

J з j

. о

0

0

J - J J 2 J i j

Тогда, с учетом вышесказанного, уравнение Эйлера (2) в параметрах Родрига–Гамильтона будет иметь вид:

J AX + G [(TNX )•( TTNX )] = Ml6 + KMY,(10)

или в неподвижной системе координат X :

X = ЛTJ-1 (KPMX + M0 - G[(TNX) • (TTNX)]) .(11)

Уравнения движения обобщенной роторной системы. Обозначим точки закрепления вала в подшипниках как a = £ x^, и b = £ xb, (рис. 2). Кроме того, будем полагать, что а3 и b3 оста-i=1

ются неизменными независимо от вращения основного вала. Обозначим вектор силы, порождаемый динамической связью (силовой функцией), в точках a и b соответственно F^a и F^b , а суммарный момент трения – M^ab . Принимая l за длину вала и используя матрицу P , несложно получить значения координат a и b :

a = c + 1 (X 1 X 3 + X q X 2 ) 1   1 x 0 2 -x 2 -x 2 +xV 1 ( X2X3-X0X, ) 1 a 2 = c2 + 2 2 22 T-J2T,         и X 0 -X 1 -X 2 +X 3 a 3 = c 3 + 1 /2

f            1 ( X 1 X 3 +X 0 X 2 ) b, = c,                             , 1   1 x 0 -x 2 -x 2 +x 2 , =        1 (X 2 X 3 -X 0 X 1 ) 2    = 2 x 0 -x 2 -x 2 +x 2 ,            ( ) b 3 = c 3 - 1 /2.

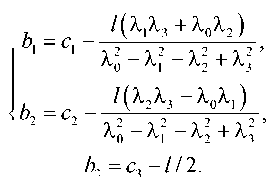
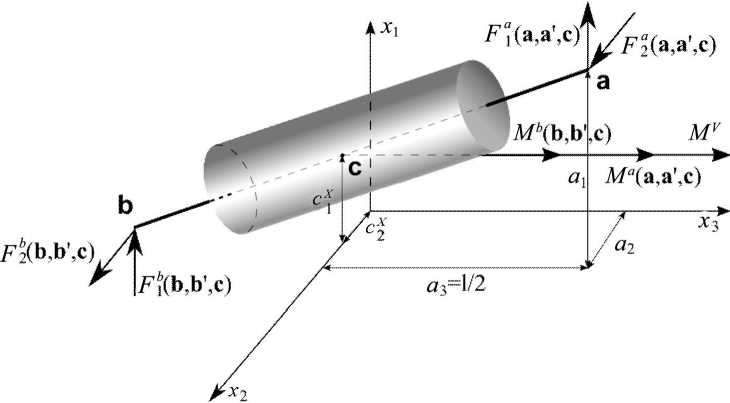
Рис. 2. Обобщенная роторная система

Будем считать, что на основной вал действует суммарный, внешний по отношению к роторной системе, момент M ^V и сила F^V . Тогда, учитывая, что суммарный момент, действующий на основной вал, можно определить по формуле:

M = M f V + M f ^ab + a x F^a + b x F^b , (13)

и используя (12), получаем:

M^X = L ( F b - F a ) + M V + M  ,

где M ^V , M ^ab , F^b , F^a – вектор-столбцы с координатами соответствующих векторов в X ;

L – матрица длин, определяемая как

	г 0	l	2 1 ( X 2 X 3 -X o X i ) " x o -X 2 -x 2 + X 3
L =	- 1	0	2 1 ( X 1 X 3 +X o X 2 )
			x 0 -X 2 -X 2 + X 2
	2 1 ( Х 2 Х з -X 0 X 1 )	2 1 ( X 1 X 3 +X 0 X 2 )	0 0
	L х 2 -x 2 -x 2 +x 2	x 0 -x 2 -x 2 +x 3 2

Исходя из вышесказанного получим систему уравнений, определяющих динамику роторной системы:

X = Л T J ' ( KP [ L ( F b - F a ) + M ab + M V ] + M 0 - G [ ( T ЛХ ) • ( T T ЛХ ) ] ) , c = 1 ( F b + F a + F V ) . m

Для окончательного построения модели роторной системы, как видно из (15), необходимо задать Fb , Fa , Mab , MV , FV . И если последние два параметра являются произвольными функциями, определяющими некоторое внешнее воздействие на систему, то первые три параметра определяются динамической связью, входящей в состав роторной системы. Очевидно, что они являются функциями состояния роторной системы Xi и ci. Задание этих функций определит окончательный вид математической модели роторной системы. В частности, Fb , Fa , M ab можно определить, основываясь на рассмотрении подшипниковых креплений ротора как трибосистем, по аналогии с тем, как это сделано в исследовании [3].

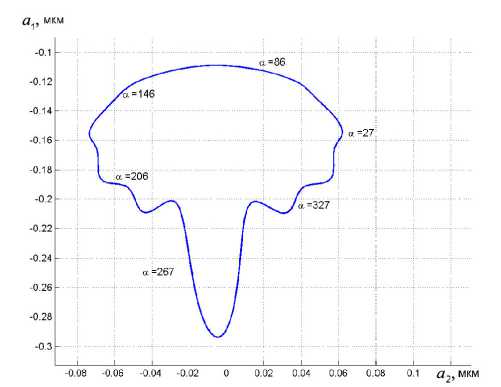
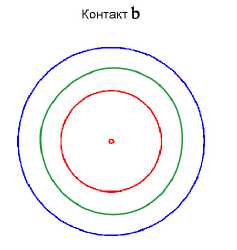
Приведем в качестве примера результат моделирования (рис. 3). При этом рассматривалось, что ротор закреплен в низкоскоростных подшипниках скольжения, а в качестве внешнего источника момента был использован двигатель постоянного тока. Качественный вид сечений ротора и статора в контактах a и b приведен на рис. 4 (в контакте a наблюдается импульсный дефект ротора и статора).

а )

Рис. 3. Результаты моделирования: а – движение ротора в плоскости а ₁ а ₂ в контакте a ; б – зависимость частоты вращения ротора от его угла поворота

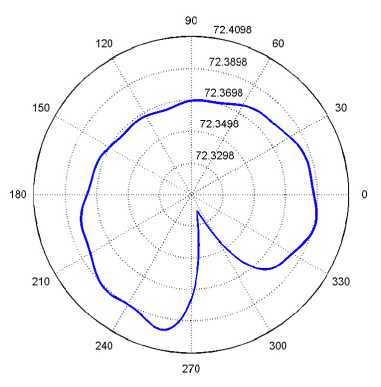
б )

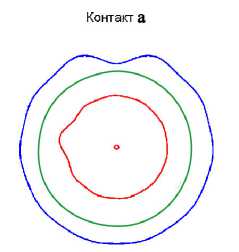
Рис. 4. Качественный вид ротора и статора в подшипниковых узлах

Из рис. 3 видно, что наличие импульсного дефекта оказывает существенное влияние не только на движение ротора в плоскости контакта a , но и на угловую частоту вращения ротора. Кроме того, виден периодический характер влияния дефекта в зависимости от угла поворота вала α .

Выводы. Предложенная формула Эйлера в параметрах Родрига–Гамильтона, позволяет осуществлять математическое моделирование пространственного движения твердых тел. При этом рассмотрение осуществляется в неподвижном базисе, что облегчает использование данной формулы. Кроме того, с точки зрения численного моделирования, ее несомненным преимуществом является отсутствие тригонометрических функций.

На основе формулы Эйлера в параметрах Родрига–Гамильтона построена модель роторной системы, позволяющая анализировать ее динамические свойства. Подобная модель может быть использована для решения различных задач, в частности задач технической диагностики.