ДИНАМИКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ В ТРАНСАКСИАЛЬНОМ ЗЕРКАЛЕ

Известно, что при расчете траекторий заряженных частиц в электростатических зеркалах возникают математические трудности, связанные с тем, что в окрестности точек поворота радиусы кривизны траекторий стремятся к нулю. При этом наклоны траекторий к оптической оси и относительный разброс энергий частиц неограниченно возрастают [1, 2]. Все эти трудности остаются в стороне, если интегрировать не уравнения траектории, а уравнения Ньютона по времени движения частиц. Численное интегрирование уравнений Ньютона значительно упрощается, если известны аналитические выражения для потенциалов, описывающие электрические поля зеркал. Для нахождения потенциалов, описывающих электростатические поля корпускулярно оптических систем (КОС), как правило, приходится решать задачу Дирихле для скалярного потенциала, удовлетворяющего уравнениям Лапласа. Потенциалы трансаксиальных КОС в цилиндрической системе координат ρ , ψ , z зависят только от переменных ρ и z и удовлетворяют уравнению Лапласа [3]:

д 2Ф +1 д Ф + д 2Ф = 0 д р2 р д р д z2

Это уравнение обычно решают методом Фурье, записывая потенциал в виде рядов функций Бесселя [3]. Однако из-за плохой сходимости рядов полученные таким образом аналитические выражения сложно использовать при численных расчетах потенциала. В работах [4–9] найдены простые приближенные аналитические выражения для потенциала трехэлектродной трансаксиальной линзы, которые с хорошей точностью описывают и поле трансаксиального зеркала. Такие зеркала можно использовать, в частности, при создании времяпролетных масс-спектрометров. Расчету свойств таких зеркал и посвящена настоящая работа.

АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ ПОТЕНЦИАЛА ПОЛЯ ТРАНСАКСИАЛЬНОГО ЗЕРКАЛА

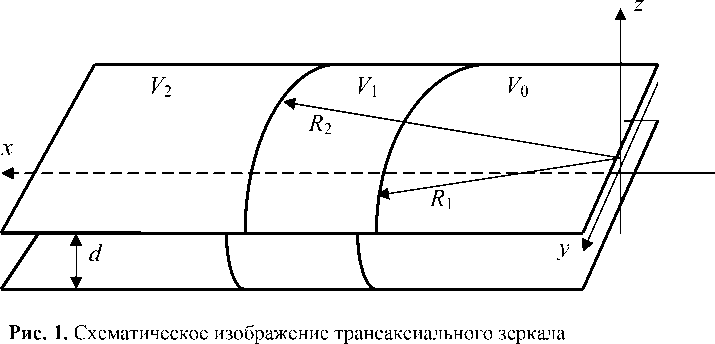
Трехэлектродная трансаксиальная линза или зеркало представляют собой две параллельные пластины, разрезанные прямыми круговыми цилиндрами радиусов R ₁ и R ₂ , ось которых совпадает с осью z [7, 9]. Такое зеркало схематически изображено на рис. 1. Показана также сопутствующая декартова система координат ( x , y , z ). Начало декартовой системы координат находится в средней плоскости зеркала, совпадающей с плоскостью ( x , у ) ; V ₀, V и V 2 — потенциалы электродов; d — расстояние между пластинами. Зазоры между электродами считаются бесконечно узкими. Вдали от краев пластин потенциал ϕ зависит только от переменных р = x ² + у ² и z .

Вводя безразмерные переменные [4–9]:

^п = ln R ’

^Z R ^,

где R = ^ R1 R2 , получим следующее уравнение для потенциала:

е - 2 ^п

д ² ф д ² ф

X '1Т

Это достаточно простое аналитическое выражение для электростатического потенциала трехэлектродной трансаксиальной линзы можно использовать и для расчета трансаксиальных зеркал.

Для расчета гармонической составляющей F(п, Z ) электростатического потенциала ф ( п, Z ) можно использовать аппарат теории функций комплексной переменной (ТФКП) [10]. При этом получается аналитическое выражение, которое дает хорошее приближение для вычисления потенциала ф ( п, Z ) , ^т-^к- оно точно удовлетворяет заданным граничным условиям Дирихле, а при р = R ( п = 0) удовлетворяет двумерному уравнению Лапласа.

В цилиндрических координатах аналитические выражения для электростатического потенциала трехэлектродных трансаксиальных линз могут быть записаны в следующем виде [7, 9]:

ф (Р, z ) =

г

г

= V + ( V - V ) р - , z , R |+ ( V - V ₂ ) P ₂ - , z , R | ,

V ^R 1

БЕЗРАЗМЕРНЫЕ УРАВНЕНИЯ НЬЮТОНА

При исследовании динамики пучка заряженных частиц в трансаксиальных зеркалах будем использовать безразмерные уравнения Ньютона [4]. Уравнения движения заряженной частицы с зарядом q и массой m в электростатическом поле в безразмерных декартовых координатах х , y , z можно записать в следующем виде:

x = Ф_х , у = Ф у Z = Ф₂ . (6)

Здесь безразмерный потенциал Φ измеряется в единицах V0 ; индексы при Φ обозначают частные производные по соответствующим координатам; за единицу длины берется величина d — расстояние между параллельными плоскостями трансаксиального зеркала; точки обозначают производные по безразмерному времени т = t/т0 , где где

τ ₀

= d

N

m

. qV ₀

<

- ’ z ’ R

V ^Rk

= —arctg π

2cos z

________d_____

π R           π R

( XT f XT dd

- I - - I

VV Rk)    V Rk)

( k = 1,2).

Начальные условия для расчета траекторий при интегрировании уравнений (6) можно задать следующим образом:

^x 0 = a , у 0 = b , ^z 0 = ⁰ ; ^x0 = 7 ²⁽¹ + e ) ^{- y} 0^{2 - Z} 0² y ₀ = Д 2(1 + e ) sin a , Z ₀ = 4 2(1 + e ) sin в .

Здесь ε — относительный разброс по энергии на входе в систему, углы α и β определяют проекции скорости на горизонтальное и вертикальное направления. При движении в средней плоскости зеркала, где z 0 = z₀ = 0, угол а определяет наклон траектории к оси x , которая является главной оптической осью зеркала, и определяется выражением:

v tg а = ^.

x ₀

Для вычисления производных потенциала, входящих в уравнения (6), используются следующие формулы для производных потенциала, определяемого выражениями (4) и (5):

2 R

д р 5 р

cos z

Rkd   d

р

I R k

+

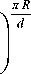
р

I R k

π R d

π R d

р I

I Rk J

р

I R k

2 π

+ 4cos —z d

5 Pk = 5 Pk др = 5 Pk x

5 x 5 р 5 x 5 р р’

5Pk -X 5р X' v;                     (U)

5 y 5 р 5 y 5 р р

π

5 Pk

5 z

d

sin z

d

π R           π R

V

р I — - I

V Rk J    V Rk J

πR

( _n XT ^р I

IRk J

π R ²

( n - V р I

R J

< R k ^J

.

π

+ 4cos — z d

Приведенные значения производных подставлялись в продифференцированное выражение (4), и таким образом определялись правые части уравнений (6).

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РАСЧЕТА

Безразмерные уравнения Ньютона (6) интегрировались численно четырехточечным методом Адамса с автоматическим выбором шага интегрирования. Разгонные точки находились методом последовательных сближений Крылова. Относительная точность интегрирования выбиралась равной 10 - 8 : 10 9 .

Были проведены численные расчеты для трансаксиального зеркала, у которого R 1 = 23 d , R ₂ = 25 d , V₀ = 1, 0 <  V 1 < 1, V ₂ <  0. За единицу длины выбиралось d = 1 — расстояние между параллельными плоскостями трансаксиального зеркала. Начальные условия моделировали точечный источник, расположенный в области вне поля в средней плоскости зеркала в точке: x ₀ =- 10, у ₀ = 1.4, z ₀ = 0. Осевая траектория направлялась под углом а = 2 ^о к оси х путем задания следующих начальных условий: , x ₀ = ^ 2 ( 1 + s ) - у 2 - z 2 , где у ₀ =- 0.0528, ^₀| < 0.001, s — относительный энергетический разброс в пучке. Объемный пучок моделировался путем следующих изменений начальных условий: |А а | <  0.001 рад, | S < 0.01. При указанных изменениях начальных условий еще достаточно хорошо выполняется параксиальное приближение.

Результаты расчетов представлены на рис. 2 и 3.

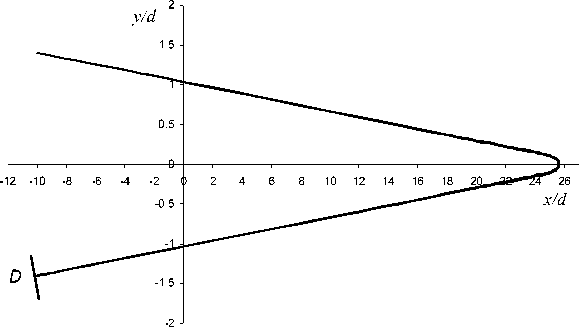
Рис. 2. Поведение пучка в проекции на среднюю плоскость зеркала

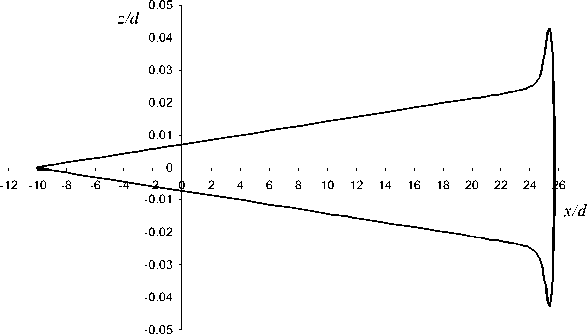
Рис. 3. Проекции крайних траекторий пучка на вертикальное направление

На рис. 2 показано поведение пучка в проекции на среднюю плоскость зеркала, а на рис. 3 — поведение крайних траекторий пучка в вертикальном направлении. Потенциалы электродов подбирались таким образом, чтобы осуществлялись пространственная и энергетическая времяпролетные фокусировки, а линейный фокус в вертикальном направлении был расположен симметрично положению источника относительно оси х . Эта ситуация осуществлялась при следующих потенциалах электродов: V 0 = 1, V = 0.969, V₂ =- 0.093. Определялось также время пролета частиц до плоскости детектора, которая проходит через точку х_к = x 0 = — 10 перпендикулярно осевой траектории пучка. Для осевой траектории ( е = 0 ) время прилета в детектор D равно T d ₀ = 53.541, а для частиц, движущихся по осевой траектории с е = 0.01 , получим T d 1 = 53.576, а при е =- 0.01 получим время прилета в детектор T d 2 = 53.556. Из этих данных видно, что с достаточно хорошей точностью осуществляется времяпролетная фокусировка по энергии и одновременно пространственная фокусировка пучка.

Безразмерные уравнения Ньютона при различных начальных условиях интегрировались по безразмерному времени τ до одного и того же конечного значения т ^ 0 = т ^ ₀ . При этом некоторые частицы не доходили до плоскости детектора, а некоторые перелетали плоскость детектора. В этом случае время прилета заряженных частиц в детектор определялось с учетом того, что вблизи плоскости детектора, где поле отсутствует, частицы движутся по прямолинейным траекториям с постоянной скоростью. Если к моменту времени т = T k о частица находилась в точке ( Х к , У к , Z k )

и двигалась со скоростью ( х_к , У_к , z_к ), то находилось расстояние до плоскости детектора. Уравнение плоскости детектора, проходящей через точку ( x_d , y_d ) параллельно оси z :

У ^- У а = ^kd ^{( 5 -} x d ),                ⁽¹³⁾

где k d =- 1/tg а. Уравнение проекции траектории на плоскость xy :

У ^- У к = ^кк ^{( 5 - х}к ),               ⁽¹⁴⁾

где к_к = У_к / 5с_к . Координаты точки пересечения этой проекции с плоскостью детектора:

5 1 = k ^k x ^k k d x d ,+ ^{Уа Ук} , У 1 = ^кк ^{( х} 1 ^- x k ) ⁺ У к . ^{(15) к}к ^{- к}а

Теперь время прилета в детектор определяется по формуле:

V( ^х 1 - ^хк ) 2 ⁺ ( У 1 ^- У к ) ^{2 T} d =^T d о ±-------------------------

.

υ xy

Здесь знак "+" берется, если частица не долетает до плоскости детектора, а знак "–", если она перелетает плоскость детектора; υ_хy — проекция скорости на плоскость xy :

22 ^и хУ =^xk ⁺ У к .

Возможно также осуществить другое поведение пучка в вертикальном направлении, незначительно изменив потенциал на отражающем электроде. Если подать на него потенциал V = 0.957 , то на выходе из зеркала получим параллельный пучок частиц. На рис. 4 показан ход крайних траекторий пучка для этого случая.

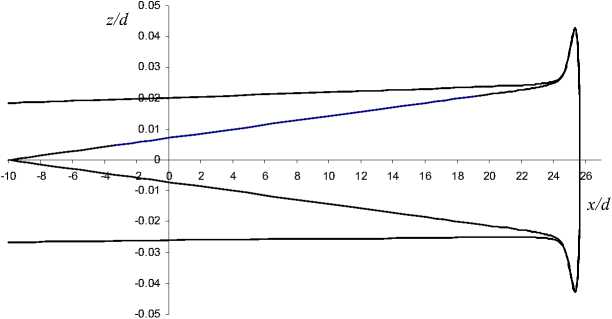
Рис. 4. Проекции крайних траекторий пучка на вертикальное направление

ЗАКЛЮЧЕНИЕ

Использование аналитических выражений, описывающих поле трансаксиальных трехэлектродных зеркал, позволило провести численное интегрирование безразмерных уравнений Ньютона для заряженной частицы в поле зеркала и таким образом изучить поведение пучка заряженных частиц в трансаксиальном зеркале. Показано, что в результате отражения в трансаксиальном зеркале можно расходящийся пучок превратить в почти параллельный и осуществить при этом высококачественную пространственно-временнýю фокусировку. Это свойство трансаксиальных зеркал можно использовать для создания высокоэффективных времяпролетных масс-спектрометров, состоящих из различных комбинаций трансаксиальных зеркал.

Работа выполнена в рамках проектов с грантовым финансированием Комитета науки МОН РК (ИРН АР09258546, ИРН АР09562705).