Динамика ротора двигателя-маховика в электромагнитном подвесе
Автор: Поляков Мирослав Вадимович
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Авиационная и ракетно-космическая техника
Статья в выпуске: 4 (56), 2014 года.
Бесплатный доступ
Приведены результаты расчета амплитуды колебаний динамически неуравновешенного ротора двигателя-маховика с кинетическим моментом 1 Н·м·с, подвешенного посредством активных магнитных подшипников. Определены силы, требуемые для удержания ротора в бесконтактном положении, и резонансные зоны в рабочем диапазоне его угловой скорости в зависимости от значений коэффициентов жесткости и демпфирования магнитного подвеса. Расчеты осуществлялись при различных диапазонах угловой скорости ротора. С помощью разработанной параметрической 3D-модели ротора для каждого диапазона определены его требуемые массогабаритные характеристики: осевой и экваториальный моменты инерции, а также его масса. Предельно допустимые значения эксцентриситета ротора, характеризующего статическую неуравновешенность, и угла между геометрической осью ротора и его главной центральной осью инерции, характеризующего моментную неуравновешенность, определялись исходя из величины массы ротора и требуемой остаточной неуравновешенности в каждой плоскости коррекции. Выявлено, что в процессе вращения ротора двигателя-маховика преобладают радиальные колебания его центра масс, вызванные наличием статической неуравновешенности. Амплитуда результирующих колебаний ротора составляет 17 мкм для диапазона частоты вращения ротора 0-9000 об/мин и 13 мкм для диапазона 0-18000 об/мин. Первая критическая скорость ротора соответствует резонансной частоте его радиальных колебаний. В диапазоне частоты вращения ротора 0-18000 об/мин присутствует дополнительная критическая скорость, обусловленная тем, что экваториальный момент инерции ротора превышает его осевой момент инерции. В закритических областях наблюдается явление самоцентрирования ротора. По результатам расчета динамики ротора в магнитном подвесе сформированы исходные данные для выбора угловой скорости ротора, воздушных зазоров в аварийных опорах, активных частях магнитных подшипников, коэффициентов жесткости и демпфирования магнитного подвеса.
Динамика ротора, электромагнитный подвес, неуравновешенность ротора
Короткий адрес: https://sciup.org/148177310
IDR: 148177310 | УДК: 62-233.2
Rotor dynamics of active magnetic bearing reaction whell
The paper presents the results of the calculation of dynamically unbalanced rotor vibration for an active magnetic bearing reaction wheel with angular momentum 1 N·m·s. Forces, required to keeping the rotor in contactless position, and the critical speeds in working angular velocity ranges are determined. Calculation is performed for various magnitudes of stiffness and damping coefficients of magnetic suspension and for various working angular velocity ranges. Required mass of rotor, axial and equatorial moments of inertia are determined by means of developed parametric 3D-model of rotor for every speed range. Maximum permissible eccentricity of the rotor, which describe the static imbalance, and maximum permissible angle between the geometrical axis of the rotor and its principal central axis of inertia, which characterize couple unbalance, are determined using the value of rotor mass and the desired residual unbalance in each correction plane. Calculation shows, that center of mass of spinning rotor perform mainly radial translations, generated due to the presence of static unbalance. The amplitude of the resulting oscillation of the rotor is 17 μm for a working angular velocity range 0-9000 RPM and 13 μm for the range 0-18000 RPM. The first critical speed of the rotor corresponds to the resonant frequency of its radial oscillations. In the range 0-18000 RPM there is an additional critical speed due to the fact that the equatorial moment of inertia of rotor exceeds the axial moment of inertia. There is the phenomenon of self-centering of the rotor in the overcritical regions. Results of rotor dynamic calculation make it possible to formulate the basic data for choosing a rotor speed range, air gaps in back-up bearings, gaps between rotor and stator of magnetic bearings, stiffness and damping coefficients of magnetic suspension.
Текст научной статьи Динамика ротора двигателя-маховика в электромагнитном подвесе
Введение. В настоящее время в двигателях-маховиках применяются, главным образом, шарикоподшипниковые опоры. Наличие механического контакта в шарикоподшипниках приводит к износу дорожек качения, вибрациям ротора, увеличению момента сопротивления вращению, необходимости смазки в зонах контакта шариков с кольцами подшипника [1].
Для устранения указанных недостатков в ряде случаев используется активный магнитный подвес ротора двигателя-маховика [1–3]. Преимущества магнитных опор – отсутствие механического контакта вращающихся и неподвижных частей двигателя-маховика, уменьшение вибраций ротора и, как следствие, возмущающих сил, генерируемых двигателем-маховиком, а также момента сопротивления вращению. Другим достоинством является возможность управления жесткостью и демпфированием подвеса [1; 2; 4]. Кроме того, нет необходимости в смазке.
На этапе проектирования при рассмотрении динамики ротора в магнитном подвесе необходимо определить силы, требуемые для удержания ротора в подвешенном состоянии, зазоры между вращающимися и неподвижными частями двигателя-маховика, резонансные зоны в диапазоне рабочих угловых скоростей ротора [1–5].
Расчет указанных характеристик осуществлялся для двигателя-маховика с кинетическим моментом Н = ±1 Н·м·с при различных значениях коэффициентов жесткости c и демпфирования b , а также диапазонах частоты вращения ротора 0– n max , где n max равняется 9 000, 10 000, …, 18 000 об/мин. В статье приведены результаты расчетов только для двух диапазонов частоты вращения ротора: n max1 = 9 000 об/мин и n max2 = 18 000 об/мин.
На схеме магнитного подвеса ротора двигателя-маховика (рис. 1) l – расстояние между радиальными магнитными подшипниками; e – эксцентриситет ротора; Δ – зазор между вращающимися и неподвижными частями двигателя-маховика [1; 6; 7].
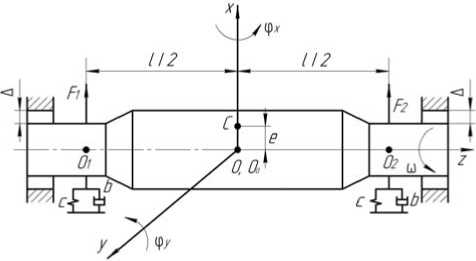
Рис. 1. Схема магнитного подвеса ротора двигателя-маховика
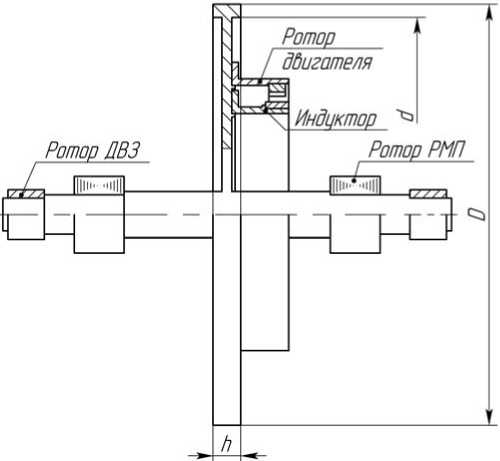
Поскольку расчет проводился для различных диапазонов частоты вращения ротора 0– n max , то для каждого диапазона определены массогабаритные характеристики ротора исходя из требуемого значения осевого момента инерции J о = Н / ω max , где ω max – максимальная угловая скорость ротора. Расчет экваториального момента инерции J э и массы М ротора в зависимости от максимальной угловой скорости ротора ω max (осевого момента инерции J о ) осуществлялся с помощью разработанной предварительной параметрической трехмерной модели ротора (рис. 2). Изменяемыми параметрами данной модели являются наружный D и внутренний d диаметры и ширина h обода ротора.
Результаты расчета массогабаритных характеристик ротора для диапазонов n max1 = 9 000 об/мин и n max2 = 18 000 об/мин приведены в таблице.
Силы и зазоры в магнитном подвесе определяются амплитудой колебаний вращающегося ротора, вызванных наличием остаточной неуравновешенности.
Амплитуда колебаний центра масс ротора под действием статической неуравновешенности [1; 7]
4 c 2 + 4 b 2 to2
А C
= e ------------2---------
^ ( 2 c - M to2 ) + 4 b 2 to 2
где ω – угловая скорость ротора.
Расчеты проводились при следующих значениях коэффициентов жесткости c и демпфирования b :
– для диапазона ω max1 = 9 000 об/мин:
с 1 = 1·104 Н/м; с 3 = 2·105 Н/м; b 1 = 10 Н·с/м; b 3 = 30 Н·с/м;
с 2 = 5·104 Н/м; с 4 = 4·105 Н/м;
b 2 = 20 Н·с/м;
b 4 = 40 Н·с/м;
– для диапазона ωmax2 = 18 000 об/мин:
с 1 = 5·104 Н/м; с 3 = 5·105 Н/м; b 1 = 30 Н·с/м; b 3 = 60 Н·с/м;
с 2 = 2·105 Н/м;
с 4 = 1,5·106 Н/м;
b 2 = 40 Н·с/м;
b 4 = 80 Н·с/м .
Из графиков зависимости амплитуды радиальных колебаний ротора, вызванных наличием статической неуравновешенности, от частоты вращения ротора при различных коэффициентах жесткости c и демпфирования b (рис. 3) видно, что для исключения явления резонанса в рабочем диапазоне nmax1 = 9 000 об/мин значение коэффициента жесткости сmin1 должно составлять не менее 4·105 Н/м. Минимально допустимое значение коэффициента жесткости сmin2 для диапазона ωmax2 = 18 000 об/мин составляет 1,5·106 Н/м. В закри-тических областях наблюдается явление самоцентрирования ротора [1; 8–15]: он стремится вращаться вокруг своего центра масс С, а не геометрического центра О (рис. 1).
Массогабаритные характеристики ротора
|
Частота вращения ротора n max, об/мин |
Осевой момент инерции ротора J о , кг·м2 |
Экваториальный момент инерции ротора J э, кг·м2 |
Масса ротора М , кг |
|
9 000 |
10,61·10–4 |
8,67·10–4 |
0,72 |
|
18 000 |
5,31·10–4 |
6,04·10–4 |
0,58 |
Рис. 2. Трехмерная параметрическая модель ротора:
ДВЗ – датчик воздушного зазора; РМП – радиальный магнитный подшипник
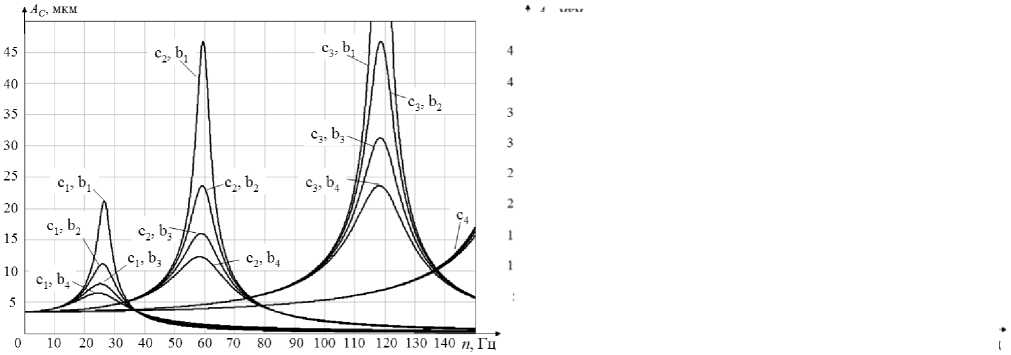
n max1 = 9 000 об/мин = 150 Гц
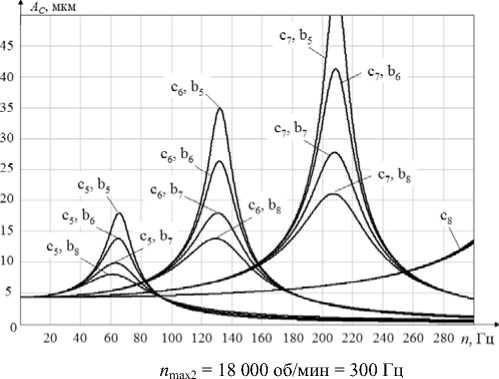
Рис. 3. Графики зависимости амплитуды радиальных колебаний ротора от частоты вращения ротора
Амплитуда вынужденных угловых колебаний главной оси инерции ротора, возникающих вследствие наличия моментной неуравновешенности [1; 7],
Как видно из графиков зависимости амплитуды угловых колебаний главной центральной оси инерции ротора, вызванных наличием моментной неуравновешенности, от частоты вращения ротора при различных коэффициентах жесткости c и демпфирования b (рис. 4), в диапазоне nmax2 = 18 000 об/мин наблюдается явление резонанса. Наличие дополнительной критической скорости ротора вызвано тем, что в указанном диапазоне частоты вращения экваториальный момент инерции ротора превышает осевой. Следует отметить, что при требуемой жесткости магнитного подшипника сmin2 = 1,5·106 Н/м указанная критическая угловая скорость ротора не лежит в рабочем диапазоне угловой скорости. В закритических областях также наблюдается самоцентрирование ротора [1; 8–15]. В диапазоне nmax1 = 9 000 об/мин экваториальный момент инерции ротора меньше осевого, поэтому дополнительной критической скорости не возникает: самоцентрирование ротора осуществляется плавно, без возникновения резонансных явлений.
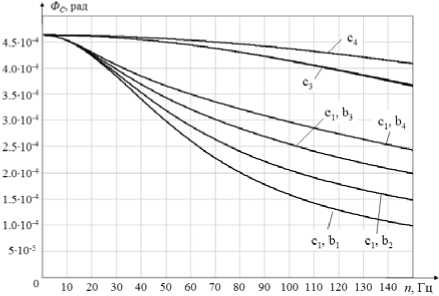
n max1 = 9 000 об/мин = 150 Гц
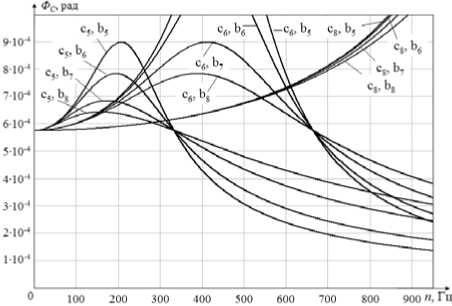
n max2 = 18 000 об/мин = 300 Гц
Рис. 4. Графики зависимости амплитуды угловых колебаний главной центральной оси инерции ротора от частоты вращения ротора
Результирующие колебания главной центральной оси инерции ротора складываются из радиальных и угловых колебаний (рис. 5).
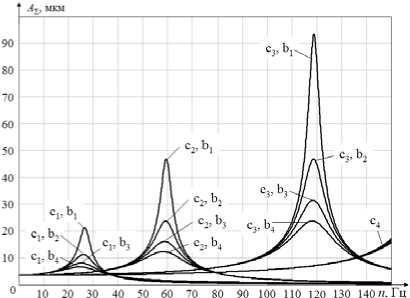
n max1 = 9 000 об/мин = 150 Гц
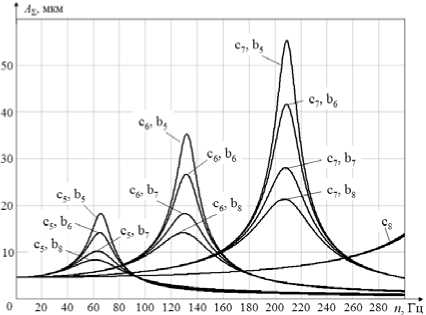
n max2 = 18 000 об/мин = 300 Гц
Рис. 5. Графики зависимости амплитуды результирующих радиальных колебаний ротора от частоты вращения ротора
Результирующая сила, которую магнитный подвес должен парировать, складывается из динамических сил, возникающих в процессе вращения неуравновешенного ротора, и веса ротора Р (рис. 6):
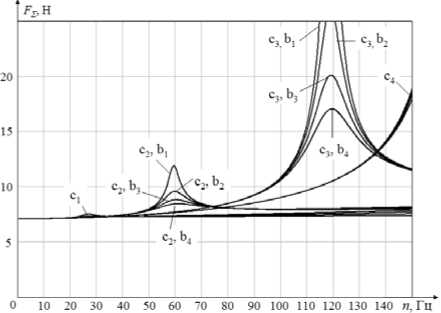
n max1 = 9 000 об/мин = 150 Гц
Рис. 6. Графики зависимости амплитуды результирующей силы от частоты вращения ротора
l
Fд = МА С m 2 +
( J э - J о ) Ф с m 2
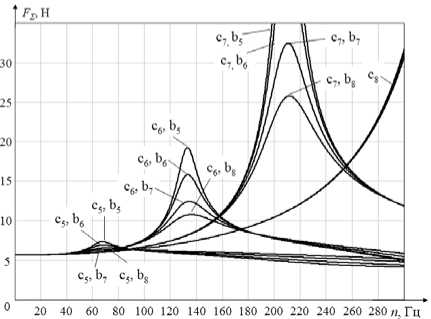
n max2 = 18 000 об/мин = 300 Гц
Заключение. Исследованиями выявлено, что для исключения явления резонанса в рабочем диапазоне частоты вращения ротора n max1 = 9 000 об/мин жесткость радиальных электромагнитных подшипников с min1 должна быть не менее 4·105 Н/м. Максимальная амплитуда колебаний центра масс ротора А С в данном диапазоне при с min1 = 4·105 Н/м составляет 17 мкм. Результирующая возмущающая сила, которую магнитный подвес должен парировать при с min1 = 4·105 Н/м, составляет 18 Н.
Для исключения явления резонанса в рабочем диапазоне частоты вращения ротора n max2 = 18 000 об/мин жесткость радиальных электромагнитных подшипников с min2 должна быть не менее 1,5·106 Н/м. Максимальная амплитуда колебаний центра масс ротора А С при с min2 = 1,5·106 Н/м составляет 13 мкм. Результирующая сила, которую магнитный подвес должен парировать при с min2 = 1,5·106 Н/м, составляет 30,9 Н.
В рабочем диапазоне частоты вращения ротора двигателя-маховика n max2 = 18 000 об/мин при с < 3·105 Н/м имеется дополнительная критическая скорость, связанная с собственной частотой угловых колебаний главной центральной оси инерции ротора.
По результатам расчета динамики ротора в магнитном подвесе сформированы исходные данные по выбору угловой скорости ротора, воздушных зазоров в аварийных опорах, активных частях магнитных подшипников, электродвигателя и датчиков.
Список литературы Динамика ротора двигателя-маховика в электромагнитном подвесе
- Журавлев Ю. Н. Активные магнитные подшипники: Теория, расчет, применение. СПб.: Политехника, 2003. 206 с.
- Леонтьев М. К., Давыдов А. Л., Дегтярев С. А. Динамика роторных систем, опирающихся на магнитные подшипники//Газотурбинные технологии. 2011. № 3. С. 16-22.
- Макриденко Л. А., Сарычев А. П., Верещагин В. П. Состояние и перспективы развития электромагнитных подшипников в ФГУП «НIIII ВНИИЭМ»//Вопросы электромеханики. 2011. Т. 120. С. 3-12.
- Мартыненко Г. Ю. Магнитные подшипники как упругодемпферные опоры роторов с управляемой жесткостью//Вiсник НТУ «ХПI». 2008. № 47. C. 111-124.
- Знышев В. В., Кирюшин А. А., Николаев М. Я. Вопросы моделирования динамики ротора на электромагнитном подвесе на макетах//Вестник Нижегородского университета им. Н. И. Лобачевского. 2009. № 5. C. 137-141.
- Сарычев А. П., Руковицын И. Г. Математическая модель ротора для анализа управления магнитными подшипниками//Вопросы электромеханики. 2008. Т. 107. С. 11-15.
- Журавлев Ю. Н. Динамика механических систем с активными магнитными опорами//Машиноведение. 1988. № 5. C. 70-76.
- Пановко Я. Г. Основы прикладной теории колебаний и удара. 3-е изд., доп. и переработ. Л.: Машиностроение. Ленингр. отд-ние, 1976. 320 с.
- Мартыненко Г. Ю. Методика экспериментальных исследований динамики ротора в комбинированном магнитном подвесе//Вiсник НТУ «ХПI». 2013. № 58. C. 125-135.
- Мартыненко Г. Ю. Исследование устойчивости движения ротора в управляемых электромагнитных подшипниках с помощью нелинейной имитационной вычислительной модели//Проблемы машиностроения. 2005. Т. 8, № 1. С. 47-58.
- Мартыненко Г. Ю. Общий подход к моделированию нелинейной динамики жестких роторов в магнитных подшипниках различных типов//Доповiдi Нацiональної академiї наук України. 2012. № 3. C. 78-84.
- Мартыненко Г. Ю. Определение силовых и жесткостных характеристик осевого активного магнитного подшипника при заданном законе управления//Вiсник НТУ «ХПI». 2008. № 36. С. 133-141.
- Magnetic Bearings and Bearingsless Drives/A. Chiba . ELSEVIER, 2005. 381 р.
- Maslen E. Magnetic Bearings/University of Virginia, Department of Mechanical, Aerospace, and Nuclear Engineering. Charlottesville, Virginia, 2000. 229 p.
- Schweitzer G., Bleuler H., Traxler A. Active magnetic bearings. Basics, Properties and Applications. Vdf Hochschulverlag AG an der ETH Zurich, 1994. 244 p.
