Динамика волчка тип-топ при вязком трении

• 1.    Постановка задачи

Рассмотрим задачу о движении неоднородного динамически симметричного шара. на. горизонтальной плоскости. Пусть г - радиус шара, s - расстояние между его геометрическим центром О и центром масс S (s = 0). Будем считать, что прямая SO с единичным ортом е = SO/s является осью динамической симметрии шара, а Л и С¹ — его экваториальный и осевой моменты инерции.

Теоремы об изменении количества движения и кинетического момента шара, условие постоянства единичного вектора восходящей вертикали д и условие безотрывности движе ния, отнесенные к главным центральным осям инерции шара, имеют соответственно вид mi + [ш, т— = —тдд + Nд + F, Jw + [ш, Jw] = [г, Nд + F] + М, д + [ш, Д ]=0, (и, д ) = 0.

Здесь т - масса шара, и и ш — векторы скорости его центра масс и угловой скорости, г = se — гд и и = и + [ш, г] — радиус-вектор и скорость нижней точки шара соответственно, д — ускорение свободного падения, N > 0 — величина нормальной составляющей реакции опорной плоскости, J = diag(A, A, C) — центральный тензор инерции шара, F и М — сила и момент трения.

«Московский физико-технический институт (национальный исследовательский университет)», 2021

При заданной модели трения

Ғ = Ғ (н, ш , у -N ), М = М (н, ш , у -N ) (2) система (1) замкнута относительно переменных — ш, у и N . Локальный анализ рассматриваемой модели волчка представлен в работах [1, 2], а глобальный качественный анализ - в работах [3-5]. Численные исследования в рамках поликомпонентного сухого трения проводились в [6]. Сравнительный анализ различных моделей проведен в [7]. В работе [8] представлен метод обобщенных диаграмм Смейла [9, 10] в задаче о движении волчка тип-топ на вязкоупругой плоскости.

При М = 0 система (1) имеет первый интеграл, представляющий собой линейную комбинацию проекций кинетического момента на вертикаль и на ось динамической симметрии шара (интеграл Желле [11])

К(ш, у) = --|-Ыш, г) = к = const, О г а при М = 0 и Ғ = 0 - интеграл энергии

Н( н , ш , у ) = 2m-² + 2(Jш■ ш) — тд( у , г) = h = const,

интеграл вида

Шз = const,

выражающий постоянство проекции кинетического момента шара и на ось динамической симметрии, а также интеграл вида

V(-■у) = ([у,-]■ [у,-]) = V2 = const,(6)

выражающий постоянство величины проекции скорости центра масс на опорную плоскость. В общем случае система (1) допускает энергетическое соотношение ■

Н = (Ғ, и) + (М, ш),(7)

и на ее решениях справедливы равенства

К = — — (М, г),(8)

О г vJ-^- у],[Ғ ■у]).<

т

Заметим, что в случае отрыва шара от плоскости (N = 0) для описания его динамики следует положить Ғ = 0, М = 0 в первых трех уравнениях (1), отбросив последнее урав нение. При этом для отслеживания возвращения на контакт следует рассматривать также уравнение z лоу )■                                          (10)

где z — высота над плоскостью нижней точки шара (в момент отрыва и при возвращении на контакт z = 0).

• 1.1.    Абсолютно гладкая плоскость

Рассмотрим случай абсолютно гладкой плоскости Ғ = 0, М = 0. Наличие интегралов (З)-(б) и геометрического интеграла

г(у) = (у, у ) = 1                                  (И)

позволяет понизить порядок системы (1) до единицы.

При к = шз(±1 — s/г) получим

2(A + ms² sin² 0)02 + W(0) = h — ^m^,                       (12)

где 0 - угол нутации (sin0 = 0 при к = шз(±1 — s/г)), a W(0) - эффективный потенциал вида

1„ 2 О2(кг — (г cos 0 — s)шз)2

^{W (0)} = ^^Ошз ⁺------- ■ 2д -----~ ^{+ т}9^{(г — scos0)}.

2                 2 A sin² 0

Функция W (0) имеет на промежутке 0 G (0,л) одну критическую точку 0 = arccosж. являющуюся точкой строгого локального минимума и определяющуюся равенством

(к — (ж—Ь) шз)² a (1—ж²)^{2    Ж}

-

к — (ж—Ь) шз a (1—ж2)    3

— с = 0.

Здесь a, b и с - параметры шара а = A Е [1/2, +№], b = - € (0,1), с = ^^ € (0, х'.

С                 г              С

Критической точке W(0) соответствуют решения уравнений движения шара на абсолютно гладкой плоскости вида v1 = v(cos wt cos Wot — sin wt cos 0 sin Wot) , v2 = v( — cos wt sin Wot — sin wt cos 0 cos Wot), «3 = v sin wt sin 0, W1 = w sin 0 sin wot, w2 = w sin 0 cos wot, w3 = const, 71 = sin 0 sin wot, 72 = sin 0 cos wot, 73 = cos 0, N = mg, где

k — (ж —b) w3

w = _a (1 - _ж2) , wo = w3 — уж.

Они определяют устойчивые регулярные прецессии вокруг центра масс, равномерно прямолинейно движущегося вдоль плоскости. При этом величина нормальной реакции опорной плоскости равна весу шара.

При k = шз(±1 — s/г) соответствующие решения имеют вид 71 = 72 = 0, 71 = ±1, wi = w2 = 0, w3 = const, v1 = v sinw3t, v2 = v cosw31, «3 = 0, N = mg,

которым соответствуют равномерные вращения шара вокруг вертикально расположенной оси симметрии, равномерно движущейся вдоль плоскости. Решения (16) всегда устойчивы при наинизшем расположениях центра масс шара (0 = 0), а при наивысшем расположении центра масс (0 = тг) устойчивы при выполнении неравенства w2 >  4Amgs/C ² [12].

• 1.2.    Плоскость с трением скольжения

Рассмотрим случай плоскости с вязким трением скольжения

F = —ки, М = 0.                            (17)

Тогда из рассмотренных в предыдущем параграфе стационарных движений реализуются только те, на которых проскальзывание отсутствует. Это равномерные вращения вокруг неподвижной вертикальной оси симметрии ((16) при v = 0) и регулярные прецессии вокруг

неподвижного центра масс ((14) при v = 0), параметры которых полностью определяются

постоянной интеграла Желле [4]: 0 = arccos у, k2

и справедливо равенство

= _—b =        ^k

,        а(1—у2) + (у — b)2,

(а(1—у2) + (у — b)2)

b — (1 —а)у      ,

2 _ ^{(b —} у^{)2 с}

Ш 3   (а — 1)у + b.

Полный параметрический анализ устойчивости этих решений и соответствующие диа

граммы Смейла представлены в [3-4]. В частности, если параметры шара удовлетворяют равенствам

1 + b > а > ^—^ ( т + bV1 + 14b + b²) ,                    (20)

то вращения с наинизшим расположением центра масс (у = 1) устойчивы при w2 < w+ (k2 < k+), а с наивысшим (у = —1) - при w2 > w- (k2 > k-), где w± = Ca T Д — b)’ k± =w±(±1 — b), а прецессии всегда устойчивы. Соответствующая диаграмма Смейла представлена на ПНР 1

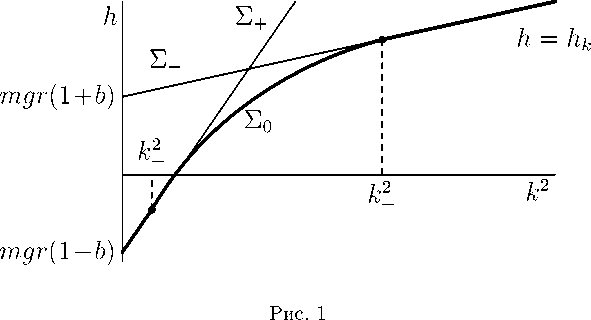
Множества У± и Уо соответствуют вращениям у = ±1 и прецессиям соответственно, жирным кривым соответствуют устойчивые движения. В случае (20) каждому значению к соответствует ровно одно устойчивое движение, точные выражения для соответствующей зависимости h = ЬДк) представлены в [3].

Все точки плоскости (к², h), принадлежащие множеству У = У+ UУоUУ-, инвариантны относительного фазового потока системы (1), а все остальные (h > h-Д эволюционируют вдоль прямой к = const в сторону уменьшения h [13]. Это обстоятельство позволяет дать глобальный качественный анализ динамики шара [4]. Например, если в начальном положении ось шара почти вертикальна, центр масс близок к наинизшему положению, а начальная угловая почти сонаправлена с осью и достаточно велика (так, что к больше бифуркцион-ного значения к-, начальное положение точки на плоскости (k²,h) лежит в окрестности У+ правее прямой к² = к-. Следовательно, при движении шара эта точка будет двигаться вдоль прямой к² = const в сторону уменьшения h до тех пор, пока не достигнет множества У-. Таким образом, в процессе движения ось динамической симметрии шара перевернется к вертикальному положению с наивысшем расположением центра масс, и шар будет равномерно вращаться вокруг нее. Аналогичным образом определяется финальное движение шара при любых начальных условиях.

Для исследования описанных переходных процессов заметим, что при М = 0 на решениях системы (1) справедливо равенство т ш3 = ^([-^, 7], ез).                                          (21)

Откуда в предположении о малости трения следует, что шз является медленной переменной, а приближенное уравнение, описывающие ее изменение, может быть получено подстановкой вместо быстрых переменных соответствующих периодических или почти периодических решений исходной системы, найденных в предположении о постоянстве медленной переменной [14,15], т.е. соответствующих стационарным движениям шара на абсолютно гладкой плоскости.

Например, если начальные условия лежат в окрестности неустойчивых вращений, то в качестве порождающих решений можно выбрать (14) с учетом (15), (13). Тогда из (21)

полагая г = 0 получим т² , ш 3 = -к—Ф(шз),

Ф(шз) = (Ь-ж) к + (а(1 - ж2) + (Ь-ж)2) шз, где при шз = ка±, а± = (±1 — Ь) 1 зависимость ж = ж(шз) определяется равенствами (13), а. при шз = кст± следует положить ж = ±1 (шз = 0).

В силу соотношений (1) справедливо неравенство шз/к > ст-, откуда следует, что функция Ф(шз) не меняет знак. Кроме того, она оиращается в ноль только в точках шз = кст±. и решение (22) стремится к ксг± при начальных условиях шз(0) ^ кст+ (шз(0) ^ к<г+) в случае к > 0 (к < 0).

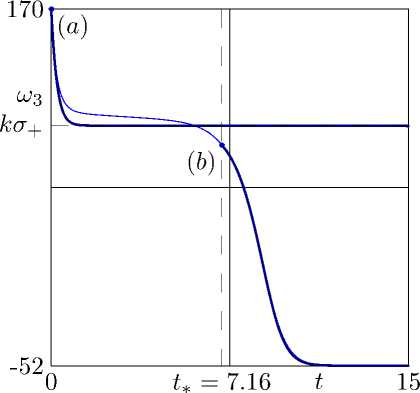
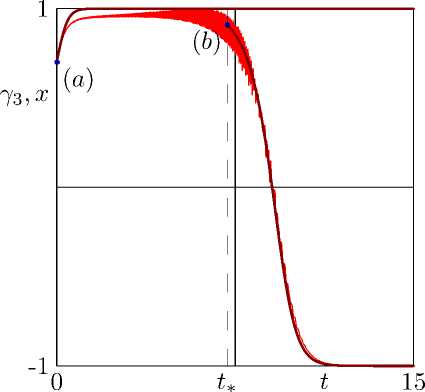
Рис. 2

На рис. 2 представлены результаты численного интегрирования уравнений движения шара с параметрами (соответствующих условиям (20))

а = 1, b = 1/3, с = 300 с^-1                               (23)

на плоскости с коэффициентом трения к = 0.1 к г/с при начальных условиях

г(0) = 0, 7з(0) = 0.7, 71(0) = 0, шз(0) = 170 рад/с, wi (0) = w2(0) = 0      (24)

(начальное значение 72(0) определяется геометрическим интегралом) - зависимость от времени проекции угловой скорости шара на ось динамической симметрии Ш3 и косинуса угла нутации 7з (тонкие кривые). Начальные условия (24) соответствуют начальному положению точки плоскости (к², И) выше прямой Е . и правее бифуркационного значения к—. Как и следовало ожидать, в численном эксперименте наблюдается переход к неустойчивым вращениям с наинизшим расположением центра масс с последующим переходом к устойчивым вращениям с наивысшим его расположением.

Жирными кривыми на рис. 2 обозначены численные решения приближенного уравне ния (22) с начальными условиями шз(0) = 170 рад/с,     (а)

шз(Д) = 85 рад/с,    (b)

и соответствующего закона изменения косинуса угла нутации. Начальные условия (25а) соответствуют (24), а соответствующее решение (22) - переходу к неустойчивому вращению. Значение t* определялось из условия равенства (25b) при численном интегрировании уравнений движения шара с начальными условиями (24). Решение (22) с начальными условиями (25b) соответствует последующему переходу от неустойчивого вращения к устойчивому.

Рассмотрим теперь случай, когда начальные условия находятся не только в окрестности окрестности неустойчивых вращений (16) (при г = 0), а в окрестности любых решений (14) (с учетом (15), (13)), отличных от (18). В этом случае из равенства (9) можно заключить, что при малом трении г так же, как и Ш3 является малой величиной, что позволяет построить соответствующее приближенного уравнение.

Из (21), (9) получим г г = —к-- m

w 3 =

-

-ксг

к—Ф(^з)     ', ma     V1 — ж22

V1 — ж2 cos wt — к—Ф(шз),

где величина ш определяется первым равенством (15), т.е.

ш = <

— 4ас(Ьх — 1)(— х + Ь) + к2 — к   шз   ,      . 2а (Ьх — 1)             ’ к € (°- ’"+’’ _____________________________ (27) V 4пс(Ьх — 1)(—х + Ь) + к2 — к    шз _         2а (Ьх — 1)          ’к    + ’

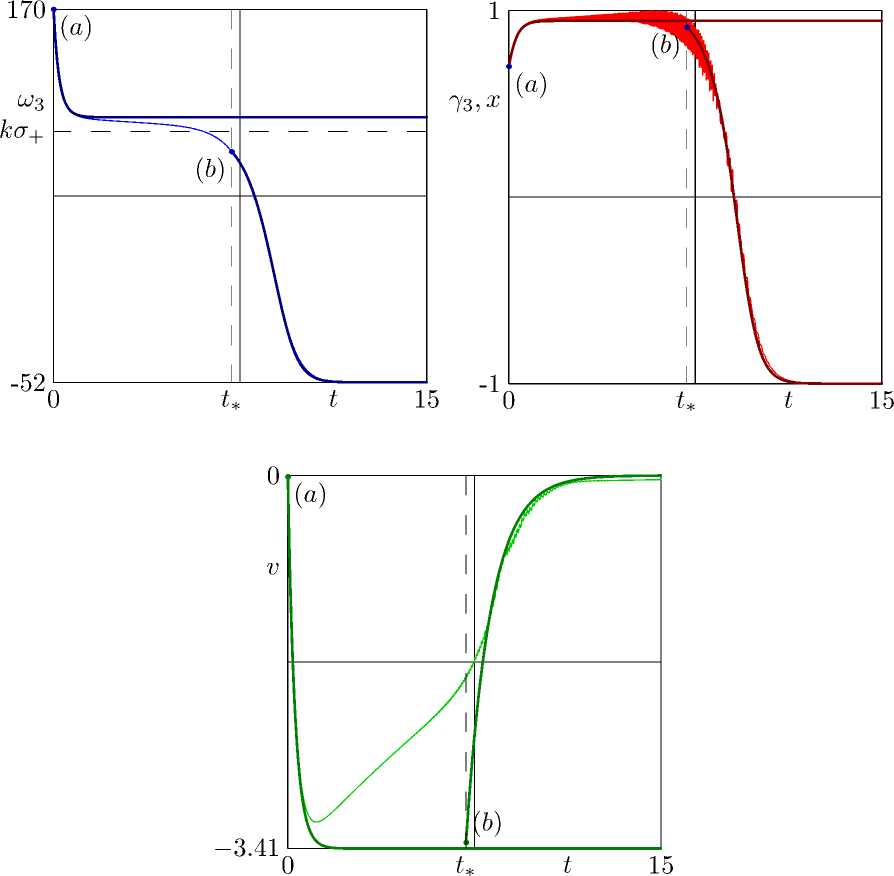
Рис. 3

Из равенства (27) при движении в области шз/к < <г. следует, что абсолютная величина ш достаточно велика и ші является быстрой величиной. Осредняя уравнение (26) по времени, получим то же уравнение (21) и равенство Г = —кг/m. Таким образом, на основном переходе от множества У. к множеству У-, вели чина г экспоненциально стремится к нулю, не оказывая влияния на изменение ориентации шара. Если же начальная точка плоскости (к²’И лежит выше множества п+ и правее прямой к² = к—, то величина ш достаточна мала, вследствие чего величина г оказывает влияние на изменение шз. Этим объясняется отклонение решения уравнений (22) от решения полной системы уравнений. На рис. 3 представлены решения системы (26) при начальных условиях г(0) = 0 м/с, (25а)

и системы (26) при начальных условиях v(t*) = -3.4 м/с, (25b), а также соответствующие решению полных уравнений движения шара величины.

В заключение заметим, что учет момента трения верчения [16] позволяет описать рассматриваемый переходной процесс без задержки на неустойчивом вращении.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (19-01-00140, 18-01-00335) и Программы фундаментальных научных исследований по приоритетным направлениям, определяемым Президиумом Российской академии наук, № 7 «Новые разработки в перспективных направлениях энергетики, механики и робототехники».