ДИНАМИКА ЗАРЯЖЕННЫХ ЧАСТИЦ В ДВУМЕРНЫХ МАГНИТНЫХ ПРИЗМАХ С УЧЕТОМ ВЛИЯНИЯ КРАЕВЫХ ПОЛЕЙ

Двумерные магнитные призмы могут использоваться в качестве отклоняющих призменных систем в призменных магнитных масс- и бета-спектрометрах. Такие спектрометры по своей схеме аналогичны призменным светооптическим спектрометрам. Они снабжаются коллиматорной и фокусирующей линзами [1–5]. Угловые дисперсии магнитной призмы по массе и энергии одинаковы и равны D' , при этом линейная дисперсия прибора определяется формулой:

D = Df 2 ,                    (1)

где f ₂ — фокусное расстояние фокусирующей линзы. Поэтому линейная дисперсия призменного прибора может быть увеличена без увеличения линейных размеров призмы за счет увеличения фокусного расстояния f ₂ .

Двумерные магнитные призмы обладают средней плоскостью, являющейся плоскостью антисимметрии магнитного поля. На рис. 1 схематически показана двумерная магнитная призма, магнитные полюса которой значительно вытянуты вдоль оси z . Поэтому в области движения пучка заряженных частиц, который входит в призму под углом α , магнитное поле призмы зависит только от двух других декартовых координат. Параллельный плоский однородный пучок заряженных частиц, движущийся в средней плоскости призмы, отклоняется призмой и выходит из нее также па-

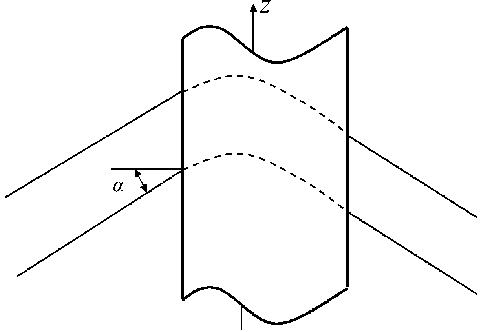
Рис. 1. Двумерная магнитная призма раллельно вследствие идентичности траекторий частиц. Таким образом, в магнитных призмах сохраняется параллельность плоских параллельных однородных пучков заряженных частиц, движущихся в средней плоскости. Сохранение параллельности объемных пучков при этом обеспечивается благодаря выполнению условия телескопич-ности [1–5].

Двумерные магнитные призмы рассмотрены во многих работах (см., например, [1–6]). Во всех этих работах магнитное поле двумерной магнитной призмы описывается с использованием векторного потенциала. Однако такое описание маг- нитного поля не является единственно возможным. В области, где отсутствуют электрические токи проводимости, ротор вектора магнитной индукции B равен нулю:

rot B = 0.                     (2)

Это позволяет определить индукцию магнитного поля B призмы как градиент скалярного магнитного потенциала ω :

B =- grad to =—V го.            (3)

где l — ширина магнитных полюсов в направлении оси x , предполагается, что в направлении оси z полюса достаточно протяженные, что и обеспечивает двумерность поля в области движения заряженных частиц. Двумерная магнитная призма с экранами и сопутствующая декартова система координат схематически изображены на рис. 2.

На рисунке магнитные экраны с потенциалом C 0 _ 0 изображены тонкими линиями, а магнитные полюса — толстыми линиями.

Дифференцируя (4), найдем компоненты вектора магнитной индукции B ( x , у ) =—V го :

РАСЧЕТ МАГНИТНОГО ПОЛЯ ПРИЗМЫ

В работе [7] были получены аналитические выражения для скалярного потенциала дефлекторных пластин с двумя заземленными экранами. Аналогичные выражения можно использовать и для скалярного магнитного потенциала ω ( x , y ) двумерной магнитной призмы с магнитными экранами:

дго _- C Т У д х " 2 d 0— 0+

, _ д го _ C В —(a4 — 1) В + ( a4 — 1) 'y = д у ~ 2d 0"           0+

ro( x , У ) =

С

2 π

arctg

πy cos

d

—

к

πx 2 а ch

d

—

πy sin

d

где

Т = 2 a (a2

~ 1)

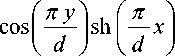
Здесь

— arctg

πy cos

d

\

πx

2 a ch-- + d

πy sin

d 7

.

0 _ 4 a ² ch^{2 П} x — d

— 4 a(a ² + 1ch ^П x sin ^{V ;} к d J

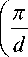
i           2 п у — 2 a cos—у + a +1, 7           d

С

±— — потенциал магнитных полюсов,

d — расстояние между магнитными полюсами, а параметр а равен

0⁺ _ 4 a ² ch^{2 П} x + d

a = exp

Г п)

+ 4 a ( a ² + 1 ) ch

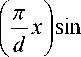
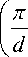
i           2 п у — 2 a cos—у + a +1, 7           d

к 2 d 7

В _ 2 a (a a

— 1) ch

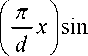
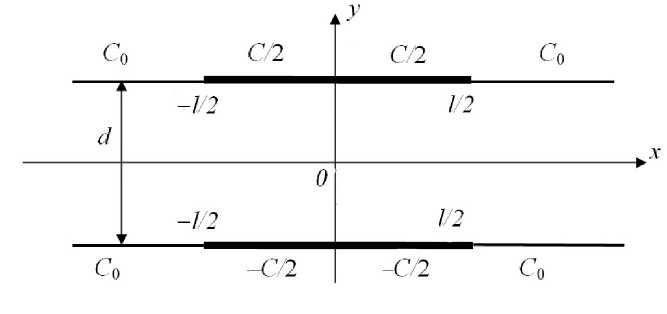
Рис. 2. Схематическое изображение двумерной магнитной призмы с магнитными экранами

Распределение магнитной индукции в средней плоскости призмы определяется выражением:

С        (a 4-1)

B y ( x ,0) = B y (- x ,0) =- -------^X-----’-------2. (8)

4 a ² ch² — x + ( a ² - 1 )

Пусть B ₀ — характерное значение величины индукции магнитного поля. Это может быть значение индукции в центре магнита при x = 0 и у = 0, которое можно измерить, например, датчиком Холла. Согласно (8), получим:

| B (0,0)1=B0 = -^.(9)

a + г      ™ о оV

Тогда выражение-- = B_z определяет без-

B0

размерную индукцию магнитного поля B _l . На рис. 3 приведено распределение безразмерной индукции магнитного поля в средней плоскости двумерной магнитной призмы для призмы с 1/ d = 6, вычисленное по формуле (8), по оси ординат отложена величина В_ly ( x ,0) .

БЕЗРАЗМЕРНЫЕ УРАВНЕНИЯ НЬЮТОНА

В нерелятивистском приближении движение заряженной частицы с электрическим зарядом е и массой m можно описать следующим дифференциальным уравнением Ньютона:

m —= е ( E + и х B ) .            (10)

Здесь r — радиус-вектор частицы, E — напряженность электрического поля, B — индукция магнитного поля, и х B — обозначает векторное произведение скорости частицы υ на индукцию магнитного поля B .

Запишем уравнение (10) в безразмерных переменных, ориентируясь в дальнейшем на рассмотрение пучков заряженных частиц с разбросом по массам и энергиям. Представим массу частицы в виде:

m = m _c(1 + y ), (11)

а энергию частицы на входе в систему в виде:

W o =- (1 + 8 ) eV o . (12)

В последних выражениях: m _c — масса "центральной" частицы, движущейся по осевой траектории, γ — безразмерный параметр, определяющий относительный разброс частиц по массе, ε — безразмерный параметр, определяющий относительный разброс частиц по энергии на входе в корпускулярно-оптическую систему (КОС), причем для "центральной" частицы у = 8 = 0. Отметим, что величина ( - eV₀ > 0 ) всегда положительная (положительные ионы вытягиваются отрицательным потенциалом). Электростатический потенциал ϕ нормирован таким образом, что он равен нулю там, где равна нулю скорость частиц, причем

Е =-V ф. (13)

Однако отрицательные потенциалы неудобно использовать при численных расчетах, поэтому потенциал ϕ мы будем везде считать положительным, при этом кинетическая энергия частиц будет равна е ϕ .

-5

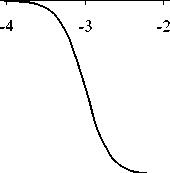
0.2    B l y ( x , 0)

-0.2

-0.4

-0.6

-0.8

-1

-1.2

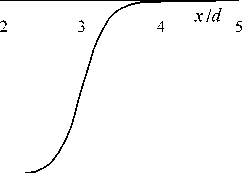
Рис. 3. Распределение безразмерной индукции магнитного поля в средней плоскости двумерной магнитной призмы с l]d = 6

Возьмем в качестве единицы длины d — характерный линейный размер КОС, V0 — характерный электростатический потенциал КОС, B0 — характерное значение величины индукции магнитного поля. Введем также безразмерное время t т =—. τ0

Теперь перепишем уравнение (10) в виде:

d d2 r _ eV0 (1 + s)    V^

т ₀ ² d т ²     m с ( 1 + y ) d V ₀ ( 1 + s )

eB_nd   d r V to

0— x .

m с ( ^{1 +} Y ) ^T o d ^{T B} о

e V ₀ , причем R ₀ d — безразмерный радиус кривизны траектории, измеренный в единицах d . Ранее мы использовали несколько иную запись безразмерных уравнений Ньютона, приведенную в [8, 9].

Отметим, что уравнение (19) имеет глубокое физическое содержание. В частности, из этого уравнения следует, что постоянное электрическое поле пространственно разделяет частицы только по энергии. В то время как постоянное магнитное поле разделяет частицы и по энергии, и по массе, причем одинаковым образом в силу идентичной зависимости от ε и γ . При этом, в силу (16), наличие разброса по энергии ε и массе γ приводит лишь к изменению времени движения частиц.

РЕЗУЛЬТАТЫ РАСЧЕТА

В этом уравнении компоненты радиус-вектора r измеряются в единицах d . Если теперь τ ₀ выбрать равным

т ₀ _ d

mc (1+ Y)

\ eVo (1 + s )’

Для расчета траекторий заряженных частиц в двумерных магнитных призмах воспользуемся следующими безразмерными уравнениями Ньютона, которые получаются из (19) при отсутствии электрического поля:

придем к уравнению

d2 r   VФ       eB0   d r „

_       + T 00        x B l.

d т ²     1 + s     m с ( 1 + Y ) d т

Здесь V Ф — безразмерный градиент безразмерного потенциала

ϕ

Ф _—.

V 0

Kz Blv ly

x _—i      =,

7(1 + s)(1 + Y)

Kz Bix

• •                         lx

У (1 + s)(1 + Y) ’ z _ K (x Bly - y Bix)

7(1 + s)(1 + Y)

В дальнейшем при расчетах будем считать потенциал ϕ и электрический заряд е положительными величинами. При этом кинетическая энергия заряженных частиц будет равна еϕ . Подставляя в (17) формулу (16) для τ ₀ , получим:

d2 r   VФ        1      2dd d r _—._ ---+ —,       =---x B dт     1 + s     (1 + s)(1 + y) Rо dт 1

Здесь

R

>j ² m c • | e^V 0 I I e • B 0

Эта величина определяет радиус кривизны траектории в точке, где индукция магнитного поля равна B ₀ , а величина энергии частицы равна

Здесь точки обозначают производные безразмерных координат по безразмерному времени τ , K — безразмерная постоянная, численное значение которой подбирается в процессе расчета. Ограничимся рассмотрением призм с симметричной осевой траекторией. Для этого положим, что в центре магнита, где y _ 0 и х _ 0, значения y _ z _ 0, а хс _ ^2. Тогда значение постоянной K , согласно (19), будет определяться выражением

K _ 4 d • (22)

R ₀

Действительно, осевая траектория пучка c y _ s _ 0 при этом будет плоской кривой, лежащей в плоскости х z призмы, для радиуса кривизны которой можно записать следующую известную формулу:

R =

(X2 + Z2 )2 ......

|xz - xz|

Отметим, что при движении заряженной частицы в постоянном магнитном поле модуль скорости не будет изменяться, поэтому выполняется соотношение

Подставляя в эту формулу y = z = 0 , получим:

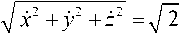
R о = - .                (24)

z

Используя третье уравнение (21) и учитывая, что в центре магнита B ly (0,0) = 1, запишем:

При этом скорость "центральной" частицы в середине магнита определяется формулой, которая согласуется с законом сохранения энергии:

d

z = XK .

2 еV 0 m _c

Подставляя (25) в (24) и х = д/2, получим в без- размерных единицах

R о = X = V2 d K K .

Результаты численного расчета траекторий частиц для призмы с Z]d = 6 представлены на рис. 4 и 5.

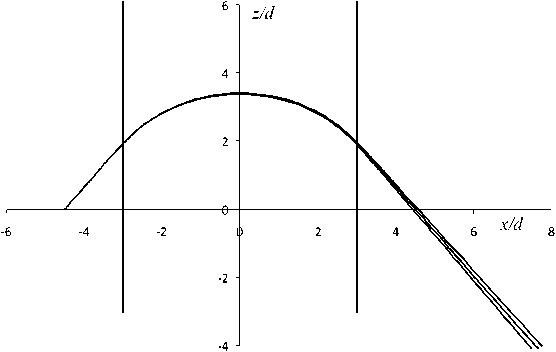
Рис. 4. Проекции траекторий частиц на сред нюю плоскость призмы c Z/d = 6

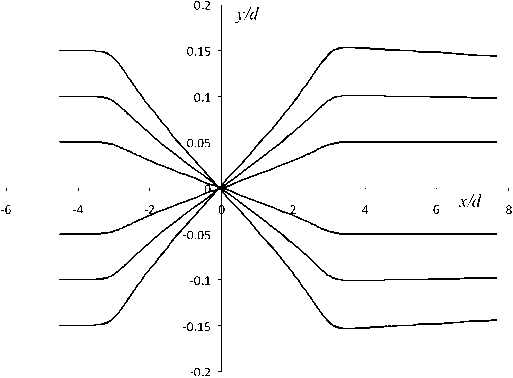
Рис. 5. Проекция траекторий частиц на плос кость xy для призмы c Z/d = 6

На рис. 4 показаны границы магнитных полюсов, а также проекции траекторий частиц на среднюю плоскость призмы для трех масс с у = 0 и у = ± 0.01. Угол падения частиц на границу магнитных полюсов равен а = 52.502 ° . Радиус кривизны траектории в центре магнита в единицах d равен 3.7813, что обеспечивает телескопичность призмы.

Проекция траекторий частиц на плоскость ху представлена на рис. 5. Здесь при наклонном входе частиц в призму частицы фокусируются к средней плоскости, образуя линейный фокус в центре магнита. При этом обеспечивается телескопич-ность призмы, а параллельный объемный пучок, входящий в призму, будет оставаться параллельным и на выходе из нее. Из рисунка видно, что условие телескопичности достаточно хорошо выполняется даже при отклонениях частиц от средней плоскости ± 0.15 d .

Угловая дисперсия призмы по массе D'_m = tg а = 1.3, что хорошо согласуется с результатами расчета и данными монографии [4]. При относительной разнице в массах у =± 0.01 угловая расходимость частиц

А а = D m Y =± 0.013 рад, (29)

т.е. чуть меньше одного градуса, что можно наблюдать на рис. 4.

Результаты расчета двумерных магнитных призм с различными отношениями l d представлены в таблице, помещенной ниже. Из приведенных данных видно, что угловая дисперсия двумерных магнитных призм по массе и энергии примерно одинакова и почти не зависит от отношения l d .

Продемонстрируем теперь универсальность полученных результатов. Основным результатом является вычисленный радиус кривизны осевой траектории в центре магнита. Для призмы с //d = 6 отношение R 0 d = 3.7813. Из формулы (20) следует, что величина анализируемой массы определяется выражением:

I d2

m _c

2 eV 0

.

Проведем вычисление анализируемой массы, используя формулу (30). Полагая, например, В ₀ = 1 Тл, eV , = 1 кэВ, величину межполюсного зазора d = 0.01 м и используя атомную единицу массы m ₀ = 1.6605 - 10 - ²⁷ кг, получим:

_m ( 1.602 - 10 " ¹⁹ - 1 ) 2 - ( 3.7813 ) 2 0.01 2 ш₀ = 2 - 1.602 - 10 " ¹⁹ - 10 3 - 1.66 05 - 10 " ²⁷

Табл. Результаты расчета двумерных магнитных призм

l / d	K	R 0 / d	α (рад)	α (град)	D ‘
4	0.5700	2.4811	0.9375	53.717	1.362
6	0.3740	3.7813	0.9163	52.502	1.303
8	0.2780	5.0871	0.9048	51.841	1.273
10	0.2214	6.3876	0.8991	51.515	1.268
12	0.1830	7.7279	0.8889	50.932	1.232
16	0.1364	10.3681	0.8813	50.497	1.213
20	0.1088	12.9983	0.8778	50.294	1.204
30	0.0722	19.5875	0.8723	49.978	1.191

ЗАКЛЮЧЕНИЕ

Физические и приборные характеристики двумерных магнитных призм рассчитаны с использованием безразмерных уравнений Ньютона и аналитических выражений, описывающих магнитное поле призмы. При этом индукция магнитного поля призмы вычисляется как градиент скалярного потенциала. Использование безразмерных дифференциальных уравнений для описания движения заряженных частиц в электромагнитных полях упрощает проведение численных расчетов и делает полученные результаты расчетов более универсальными, позволяя исключить несущественные параметры. Рассчитаны корпускулярно-оптические свойства двумерных магнитных призм с магнитными экранами в телескопическом режиме фокусировки с учетом влияния краевых полей магнита.

Работа выполнена в рамках проекта с грантовым финансированием Комитета hovku МОН РК (ИРН АР09258546).