Динамика жесткого ротора свободной турбины двигателя НК-14СТ-10 с применением демпферов опор

вильном выборе параметров улучшают вибрационное состояние агрегата с минимальными затратами на модернизацию его опор.

ГДД имеют малую массу и габариты, просты в изготовлении, надежны и эффективны при работе, имеют несколько конструктивных исполнений с разницей демпфирующей способности в сотни раз – все это позволяет гибко применять их для конкретных условий эксплуатации. ГДД позволяют успешно проходить области повышенной вибрации при вынужденных колебаниях системы [3]. Ранее исследовались колебания жесткого ротора в опорах с ГДД, однако ротор рассматривался фактически как материальная точка (Гантер, Моухэн, Хан и т.д.) [4]. Исследование динамики жесткого ротора СТ на подшипниках качения с ГДД с учетом реальной геометрии позволяет выбрать оптимальную конструкцию демпфера, спрогнозировать поведение системы “ро-тор-подшипники” при эксплуатации и является важной задачей увеличения ресурса ГПА.

Для рассмотрения была принята СТ двигателя НК-14СТ-10 (рис. 1), в опоры которой возможно установить ГДД с минимальными доработками корпуса подшипников.

В общем случае вынужденные колебания зависят от статической (смещение центра тяжести от оси вращения) и динамической (несовпадение главной центральной оси инерции с осью вращения) неуравновешенностей. Рассмотрим малые колебания ротора (рис. 1) около положения равновесия. Неподвижную систему координат OXYZ выбираем так, чтобы ее начало совпало с центром левой корпусной втулки демпфера. Вводим допущения: угловая скорость ротора постоянна и ротор не имеет осевых перемещений.

Дадим ротору произвольное смещение. Координаты центра масс правого вибратора обозначим x₁ и y₁ , координаты центра масс левого виб-

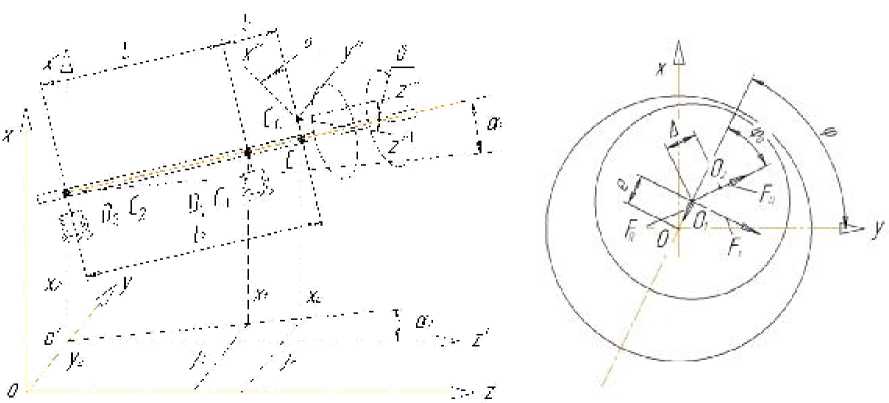
Рис. 1. Расчетная схема ротора СТ

ратора – x₂ и y₂ , координаты центра масс ротора - х_с и у_с . Вал рассматривается как абсолютно жесткое тело [5]. Угол между проекцией оси ротора на плоскость yz и осью OZ назовем а 2 ; угол между осью ротора и ее проекцией на плоскость xz обозначим а 1 . Положение опор определяется расстояниями L между ними и l ₁ , l ₂ – от соответствующей опоры до центра масс.

Если обозначить через х и у координаты точки геометрической оси ротора, лежащей на пересечении этой оси с плоскостью, перпендикулярной к оси вращения и проходящей через центр масс ротора, то координаты центра масс будут:

x_C = x + А • cos to t y_C = y + А • sin to t , где А - смещение центра масс относительно геометрического центра.

Выразим координаты центра масс и углы через независимые координаты x_1, y_1, x_2, y₂ :

LL

У с = у 1 • ^2 ⁺ у 2 • — ⁺ e ^{cos to} t ;

m • x_C = - С 1 х 1 - С ₂ х ₂ - F R 1 cos ф -

F R ₂ cos ф + F _{T 1} sin ф + F _{T 2} sin ф ;

m • У с = ^- С 1 У 1 ^{- С} 2 У 2 ^- F R 1 sin Ф ^-

FR2 sin ф - FT1 cos ф - FT2 cos ф, где FR 1, FR2, Ft1 , FT2 - радиальные и тангенциальные составляющие усилия в демпферах подшипников 1-й и 2-й опор; С1 , С2 – жесткости упругих элементов демпферов 1-й и 2-й опор; m – масса ротора СТ. Усилия в ГДД являются сложными нелинейными функциями от перемещения и определялись с учетом конвективных сил инерции смазочного слоя по методике, изложенной в работе [4].

Подставив найденные значения x_C и y_C в дифференциальные уравнения, получим:

m ( l 1 x₂ + 1 ₂ Х 1 ) + С 1 х 1 L + С ₂ х ₂ L + F R 1 L cos ф +

+ F R ₂ L cos ф - F _{T 1}L sin ф - F _{T 2} L sin ф =

= m А L to ² cos to t ;                            (2)

xr = x • L2 + x, • L^ + e sin tot;

C 1 L 2 L

a i

= y 2-- y l + g cos( to t - 0 );

m ⁽ l 1 y 2 ^{+ 1} 2. y ! ) ^{+ С} 1 У 1 ^{L + С} 2 У 2 ^{L + F}R 1 ^L sin ф ⁺ + F R ₂ L sin ф + F _{t 1} L cos ф + F _{T 2} L cos ф =

= m А L to ² sin to t .

а1

x2 l x1 + 5 sin(tot - 0)

где 5 - малый угол наклона оси C 0 Z к оси вращения, а 0 - угол между осью C 0 X и направлением CC ₀ .

На основании теоремы о движении центра инерции [6] можно написать два дифференциальных уравнения:

Переходим к составлению дифференциальных уравнений малых колебаний ротора вокруг главных центральных осей инерции. Главные моменты количества движения системы с точностью до малых величин первого порядка малости включительно будут:

L X

= ITocx + IPtoa2; LY

= I T o c ₂ - 1 P toa 1 ;

LZ = IPto, где IP – полярный момент инерции относитель-

но центра масс ротора; I_T – поперечный момент инерции относительно центра масс ротора.

Используя теорему об изменении главного момента количества движения в относительном движении к центру инерции [6] и подставляя выражение (1) получаем:

I p to (y 2 — y i ) + I t ( X 2 — X i) — С i х 1 1 1 L + С 2 х 2 1 2 L — - F R 1 1 1 L cos ф + F R 2 1 ₂ L cos ф — F_T11 1 L sin ф +

+ F _{T 2} 1 ₂ L sin Ф = ( I T — I P ) 5 L to 2 cos( to t — 9 ); (4)

I _P ^{to (}x 2 ^— x j ) ^— I T ^{( y}2 ^— .У 1 ) + С 1 y 1 ¹ 1 L ^— С ₂ y ₂ ¹ ₂ L +

+ F R 1 1 1 L sin ф — F R ₂ 1 ₂ L sin ф — F _{T 1}1 1 L cos ф +

+ F _T 2 1 2 L cos ф = ( I P — I T ) 5 L to ² sin( to t — 9 ).     (5)

Для решения уравнений (2) – (5), которые представляют малые колебания ротора, удобно перейти к полярным координатам ( e, ф ), которые связаны с декартовыми координатами соотношениями:

x i = e i • cos ф , i = 1,2; y i = e i • sin ф , i = 1, 2,

Дифференцируя выражения (6) дважды по времени и подставляя результаты в уравнения (2) – (5), получим систему из 4-х нелинейных уравнений движения жесткого ротора с четырьмя степенями свободы на опорах с ГДД. Рассмотрим случай прямой синхронной прецессии:

e 1 = e ₂ = 0; e 1 = e₂ = 0;

ф = to; ф = 0; ф = tot + ф0

где ф 0 - постоянная интегрирования, определяющая собой сдвиг фаз между возбуждающей силой Р ц = М • А • to и вызываемым ею перемещениям вибратора e .

С учетом этих допущений уравнения (2) – (5) примут вид:

F 1 cos( to t + ф ₀) — F ₂ sin( to t + ф ₀) = G cos to t ;

F 1 sin( to t + ф ₀) + F ₂ cos( to t + ф ₀) = G sin to t ;

F 3 cos( to t + ф ₀) + F ₄ sin( to t + ф ₀) = A cos( to t — 9 );

F ₅ sin( to t + ф ₀) + F ₄ cos( to t + ф ₀) = — A sin( to t — 9 ).

где

F i = L ( С i e i + С 2 e 2 + P R 1 + P R 2 ) — m to ²( 1 1 e 2 + 1 2 e i );

F 2 = L ( F < 1 + F t 2 );

F 3 = to ² ( e 2 — e i )( I p — I_T ) + L ( С 2 e 2 1 2 — С 1 e i 1 1 + P R 2 1 2 — P R 1 1 1 );

F 4 = L ( F t 2 1 2 — F t 1 1 1 );

F 5 = L ( С 1 e i 1 1 — С 2 e 2 1 2 + F R 1 Ц — F R 2 1 2 ) — to ² ( e 2 — e i )( I P — I T );

A = ( I P — I_T ) to ² L 5 ;        G = mL Ato ².

Полученную систему нелинейных уравнений аналитически решить невозможно, поэтому воспользуемся методом численного решения в среде математического пакета MATLAB. Составленная программа позволяет осуществлять поиск всех корней в заданном диапазоне изменения величин e1,e2,0 . Начальные параметры задавались из решения задачи о колебаниях жесткого ротора СТ на ГДД как материальной точки из работы [4].

По изложенной методике были определены амплитудно-частотные характеристики (АЧХ) ротора СТ (рис. 1). Исходные данные для расчета: m = 255 кг , C 1 = C ₂ = 10 9 , L = 0,465 м , 1 1 = 0,036 м , 1 ₂ = 0,501 м , I P = 5,489 кг м ² , to _РАБ = 860 рад / сек , I_T = 19,291 кг м ² . Моменты инерции и масса получены по трехмерной модели ротора, остальные параметры взяты из чертежей серийной СТ.

Результаты расчетов представлены в виде совмещенных графиков (рис. 2), на которых верхний левый рисунок – это АЧХ жесткого ротора с ГДД, рассчитанные по описанной выше методике, а нижние рисунки – соответственно значение угла ф 0 и коэффициента передачи Ц , показывающего, во сколько раз усилие, передаваемое на корпус через демпфер, больше статической неуравновешенности ротора. Верхний правый рисунок показывает АЧХ ротора, рассчитанные согласно методике [4] со всеми вышеприведенными параметрами и дается для качественного анализа корректности работы программы.

По оси абсцисс всех графиков отложена безразмерная частота вращения ротора to = toto _РАБ . По оси ординат для всех верхних графиков показана безразмерная амплитуда колебаний Б = e/ 5 0 , где 5 0 - зазор в демпфере. Сплошной линией показаны результаты расчета для первой опоры, а штриховой линией для второй опоры. Расчет произведен без учета влияния инерции жидкости (параметр инерции

to5)2 Р л ст =------= 0 , где Ц0 - динамическая вяз-

Ас кость жидкости, р - плотность жидкости) и при относительном дисбалансе U = — = 0,3 . При 50

расчетах варьировался только параметр демп- фирования B =

³ LB.

4 mtoРАБ I 50 J где D – диа-

метр вибратора, L_B – длина вибратора,.

Анализ рисунков 2-7 показывает, что полученные зависимости не противоречат известным решениям [4] и существенно уточняют картину вынужденных колебаний системы “жесткий ротор СТ - ГДД”.

Кроме этого отметим, что при использовании короткого ГДД в случае полного охвата с выбран-

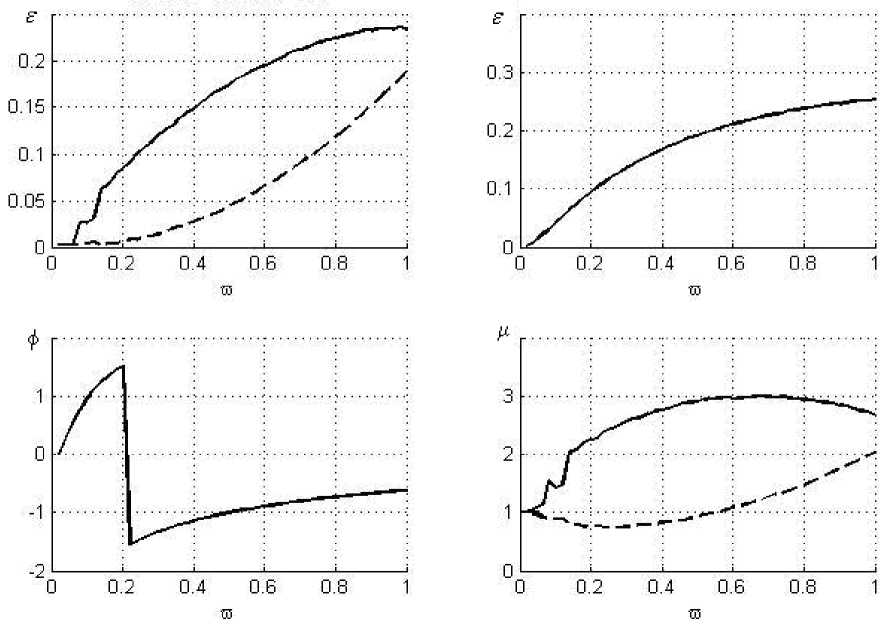
Рис. 2. Результат расчета ротора СТ для короткого ГДД при полном охвате a = 0; B = 0.05; U = 0.3

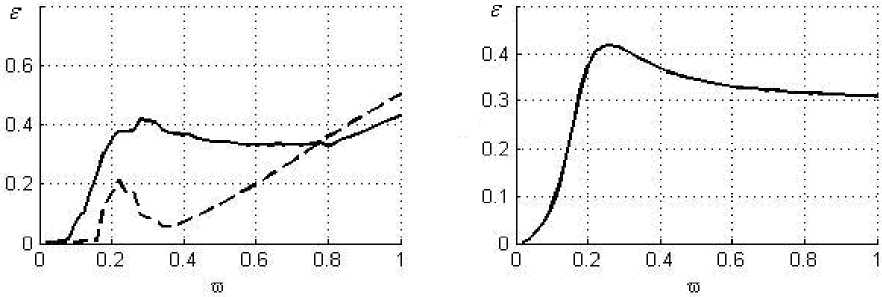
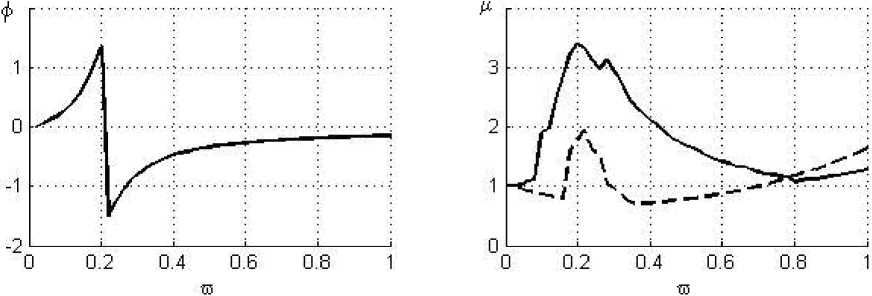
Рис. 3. Результат расчета ротора СТ для короткого ГДД при полном охвате a = 0; B = 0.01; U = 0.3

ными параметрами выгодным оказалось пониженное демпфирование (рис. 4). В этом случае значения коэффициентов передачи по обеим опорам на рабочем режиме не превышают единицы, а ампли- туда колебаний растет, но находится в приемлемых границах. Более высокое значение параметра B приводит к передемпфированию (рис. 2, 3) и усилению передаваемых на корпус усилий.

Рис. 4. Результат расчета ротора СТ для короткого ГДД при полном охвате a = 0; B = 0.005; U = 0.3

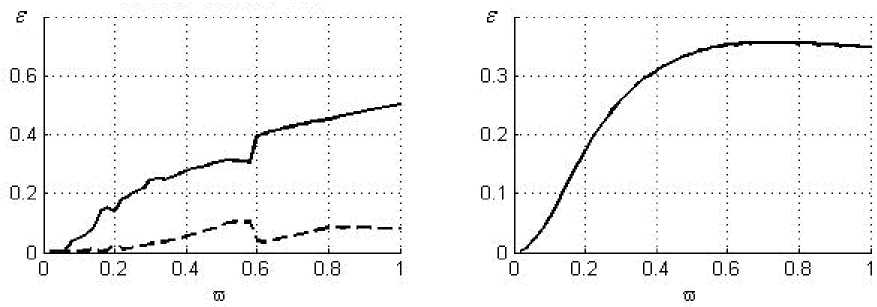
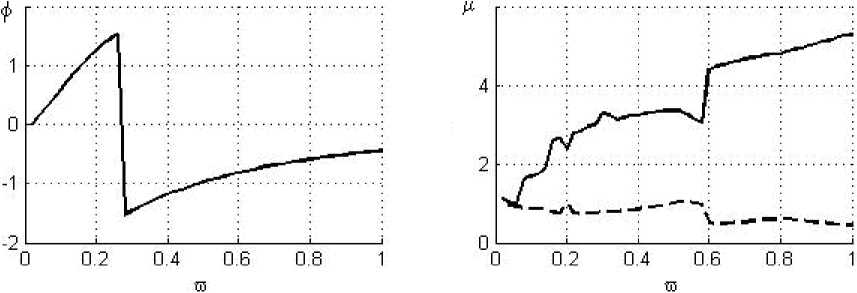
Рис. 5. Результат расчета ротора СТ для короткого ГДД при половинном охвате a = 0; B = 0.05; U = 0.3

При оценке короткого ГДД в случае половинного охвата можно указать на нарастающее увеличение зон неустойчивости (рис. 5-7) по мере снижения демпфирования. На графиках эти зоны характеризуются участками внезапного изменения знака приращения функции с постепенным возвращением к нормальному виду. Это говорит о недостаточном демпфировании,

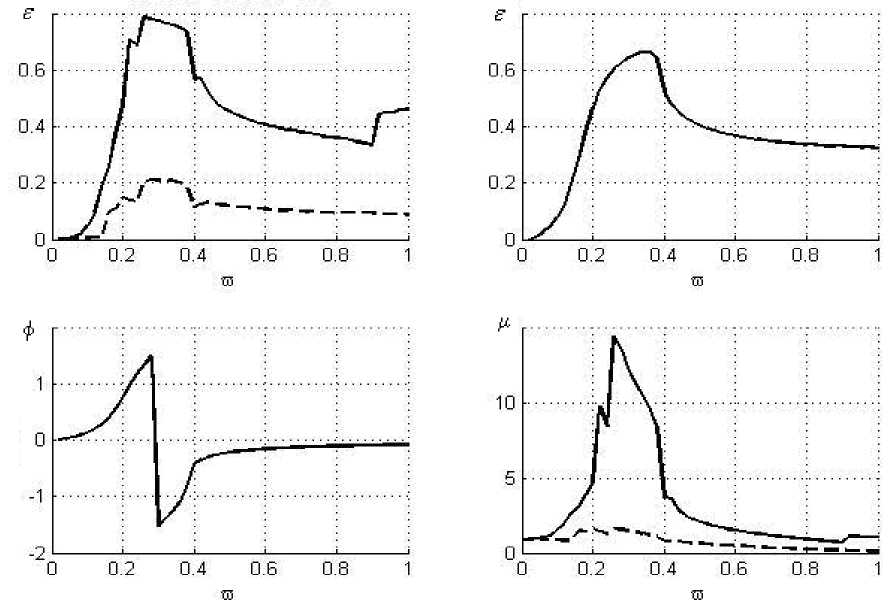
Рис. 6. Результат расчета ротора СТ для короткого ГДД при половинном охвате a = 0; B = 0.01; U = 0.3

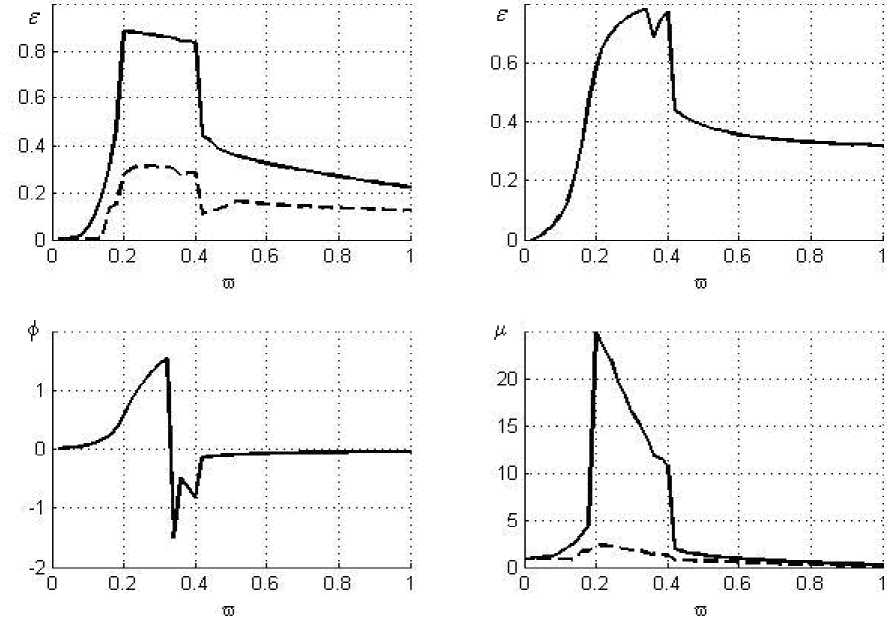
Рис. 7. Результат расчета ротора СТ для короткого ГДД при половинном охвате a = 0; B = 0.005; U = 0.3

что ведет к разрыву масляной пленки под воздействием радиальных сил, появляющихся в ГДД с половинным охватом. Такое положение объясняется большим влиянием безразмерного параметра демпфирования B на АЧХ из-за наличия в формуле радиальной силы добавки, не зависящей от инерции жидкости. Следствием этого же является высокие значения коэффици- ента µ на всем рабочем диапазоне частот вращения, что приводит к невозможности применения короткого ГДД при половинном охвате с такими параметрами (в первую очередь жесткости С1 , С2 и зазорδ0 ) и требует проведения оптимизации. Отсутствие срывных зон (рис. 5-6) на АЧХ, полученных в [4] при всех прочих равных условиях обуславливается заложенными в этой методике допущениями.

ВЫВОДЫ

• 1.    Получено решения задачи вынужденных колебаний ротора СТ с ГДД в опорах с учетом нелинейности гидродинамических сил.

• 2.    Показано, что так же, как и в одномассовом роторе, могут возникать срывные режимы работы.

• 3.    Необходимо дальнейшее проведение многоплановой оптимизации конструкции и параметров ГДД, что позволит успешно внедрить их

в опоры СТ и конечном счете во многом решить задачу увеличения ресурса всего ГПА.