Direction finding in satellite systems

In satellite technologies the problem determination of coordinates a source a radio emission (SRE) which can settle down both on Earth surface, and on the aero-space carrier [1] is actual.

Method determination of location SRE

For measurement of coordinates the SRE (corners α and β in topocentric system of coordinates, Fig. 1), B g located in a point the phase radio direction finder established onboard a communication

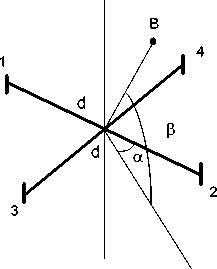
Fig. 1. Antenna arrays artificial satellite (ASE), has to have two couples antennas 1-2 and 3-4 with mutually perpendicular bases. Shift of phases between E.D.S., induced in antennas 1-2 and 3-4, [2]:

2⋅π⋅d2

Δψ  =       ⋅sinα⋅cosβ,     Δψ   =       ⋅cosα⋅cosβ(1)

νν

Where: d – base of antennas 1-2 and 3-4; – length of a wave an accepted signal.

Corners α and β from (1):

α =arctgΔψ1-2,         β =arccos ν ⋅ Δψ12-2+Δψ32-4.(2)

Δψ3-4

Having placed an antenna arrays on a geostationary ASE it is possible to define the direction on SRE concerning an ASE [3 … 6]. For determination of coordinates SRE it is necessary to calculate its coordinates in geocentric system of coordinates taking into account ellipticity of Earth

For calculation of required width and longitude of a source signal we will address to Fig. 2 [7]. Transition to the geocentric demands modification of expressions (2) therefore corners α and β pay off on formulas from topocentric system of coordinates:

α = arctg ^{Δ ψ 3 - 4} , β = arcsin ^ν ⋅ Δ ψ 1² - 2 + Δ ψ 3² - 4 .               (3)

Δψ1-2              2 ⋅ π⋅ d

Here α = 90 – α 1 ; β = 90 – β 1 .

The point D_g lies in the plane of the equator and is the projection of a point B_g. The angle φ of the triangle B g OD g is the breadth of the signal sou rce. Th e longitude λ o f the si gnal source is λ = λ sp + λ g , where λ_g – angle triangle C_gOD_g; λ_sp – longitude of the satellite. If the satellite is on the Greenwich Meridian, λ sp =0. The point C g on the line R1 is a pr ojection of a p oint D g on the meridional plane. Note that R1=42253,135 km [8].

To determine λ g refer to the section of the Earth meridional plane (Fig. 3b). In the triangle K g ON g angle α is calculated according to the formula

Segment K g N g is perpendicular to the plane of the equator. Required in this triangle is the n-end. Fig. 3a shows the plane spheroid with minor radius n, at an angle α to the plane of the equator. Semiminor axis n intersects the plane of a triangle B g AO at the same angle α to the plane of the equator. In – 656 –

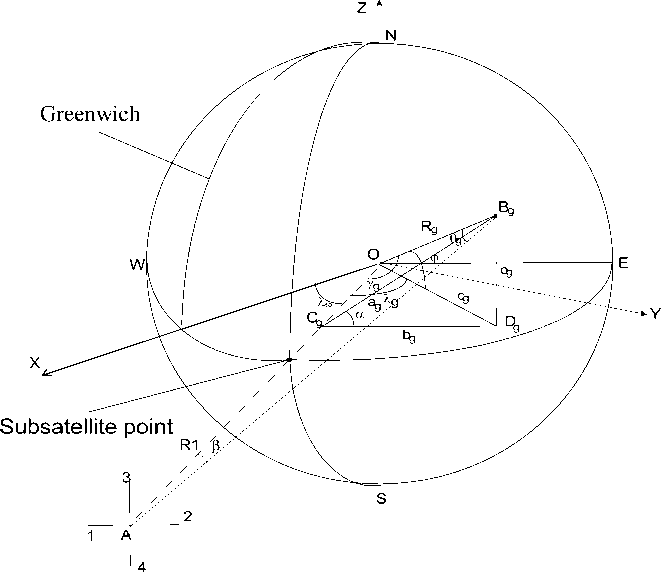
Fig. 2. Geometrical ratios

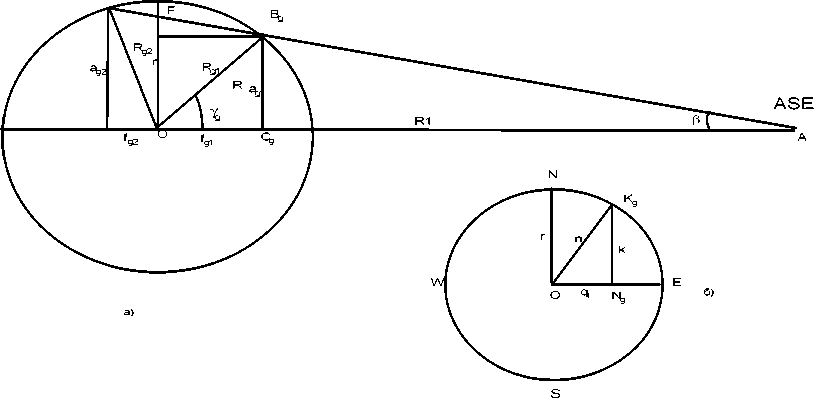
Fig. 3. Additional geometric constructions to calculate the coordinates of SRE with regard to the ellipticity of the Earth the triangle BgAO angle β is calculated according to the formula (3). The required Fig. 3a is a Rg party in the triangle BgAO.

Calculation of latitude φ and longitude λ includes the following 7 stages.

1. Is the point of intersection (Fig. 3b) minor axis n and arc spheroid, the solution of systems of two equations

k = q • tga

k = r 411 - qT

R2

where the first equation describes the minor axis, and the second is arc of a spheroid.

The solution (4) has two roots

q, = r • R •

tg ²aR ² + r²

q ₂

- r • R •

tg aR ²+ r²

Further used only positive root, since a negative value belongs to the opposite part of a spheroid.

Substituted q₁ in any of the equations (4), we obtain the value of K. The semiminor axis n of a right triangle K g ON g is equal to:

n = д/ k ² + q 1 .

2. Is the point of intersection (Fig. 3a) direct Rl, which is given by the equation ag = tg(R1 – fg) and arc spheroid by solving the system of two equations:

a g = tg ( R1 - f g ) '

2 f_g a^g = n ■ v^{1 -} Re

>

Solution of the quadratic equation

tg ² в + n ^). f g ² - 2 • R 1 • tg ² в • f g + ( tg² в • R 1 ² - n ² ) = 0, R J

are the two roots f g1 и f g2

g fg 1 =                  2

² • ( tg ² в + n 2 )

R

,

g fg2 =               й2    ,

2 • ( tg ² в + n 2 )

R

where D = (2 • R 1 • tg ² в ) ² - 4 • ( tg ² в + n r ) • ( tg ² в • R 1 2 - n ²).

R

From Fig. 3a and (9) follows that, in further calculations will need the root f g1 meaning equal side OC_g. Substituting f_g1 into any equation of system (7), we obtain the value of the side a_g1, then from a right-angled triangle B g OC g , we find R g1 :

^Rg 1   agR + f g²^ .

• 3.    From right-angled triangle B_gC_gD_g (Fig. 2) we find o_g:

• 4.    From right-angled triangle B g OD g we find latitude φ of SRE:

• 5.    From right-angled triangle B_gOD_g we find c_g:

• 6.    From right-angled triangle B g OC g , angle λ g : f

o g = a g 1 • sin ^a -

Ф = arcsin ^.

Rg 1

Cg =            .

• X, = arccos —.

• 7.    Longitude λ of SRE:

cg

λ = λsp + λg.(15)

In geocentric system of coordinates (Fig. 2):

• x = cgcosλ, y = cgsinλ, z = og.(16)

Conclusion

Thus, the described technique relying on use onboard the spacecraft of an antenna arrays, allows to solve a problem determination of coordinates of the Source a radio emission.

Work is performed with financial support of the Ministry of Education and Science of the Russian Federation in the Siberian federal university (Contract No. 02.G25.31.0041).