Direction-of-Arrival Estimation for Stratospheric Platforms Mobile Stations

Published Online August 2014 in MECS DOI: 10.5815/ijcnis.2014.09.03

Mobile location determination has become an important technology because of its commercial potential. It opens the way for Location-Based Services (LBS) where mobile positioning is applied in cellular networks. In addition, it can be considered as a motivating factor in home zone calls, traffic locating and network planning as well as assistance in handover that the network operators would get from this technology [1]. In terrestrial systems, there are various means of mobile positioning, which can be divided into two major categories – network based and handset based positioning methods. The network based technology is used to position the mobile device may be by using multiple basestations measuring simultaneously or the mobile station measures multiple basestations and examples are the Angle of Arrival (AOA) and Time of Arrival (TOA) / Time Difference of Arrival (TDOA) approaches.

In the mobile terrestrial system, the propagation environment for positioning and localizing mobile stations is very difficult which affect the accuracy of location information. This is due to the multipath propagation and the absence of the direct line-of-sight signal most of the time. The direct line-of-sight component is characterized by its larger amplitude relative to the reflected components and the error in the Direction-of-Arrival (DOA) estimation is very sensitive to these multipath components. On the other hand, satellite systems suffer from the very large distance between the mobile station and satellite although the better propagation scenario between them. This distance may be in the order of hundreds of kilometers for the low-earth orbit satellites. Recently, an innovated communications system based on utilizing high altitude stratospheric platforms has a great interest especially for mobile and wireless data communications. The platforms are known under different names as High-Altitude Platforms (HAPs), High Altitude Aircraft and Airships (HAAS), High Altitude Aeronautical Platforms (HAAPs), High Altitude Long Endurance Platforms (HALE Platforms), Stratospheric Platforms (SPs), etc [2-11]. They are located at 17–22 km above the earth surface and ITU has allocated specifically for HAPs services the spectrum of 600 MHz at 47/48 GHz (shared with satellites) worldwide. HAPs are considered nowadays as a substantial part of the future integrated terrestrial/satellite networks for providing wireless communication services. The quasi-stationary aerial platforms operating in the stratosphere preserve many advantages of both terrestrial and satellite systems but also provide special advantages of their own. Mobility on demand, large coverage, payload reconfigurability, capability of frequent take-offs and landings for maintenance and upgrading and very favorable path-loss characteristics (with respect to terrestrial or satellite systems) are the main features which make HAPs attractive for a large class of applications and services. Therefore in this paper, the SPs will be tested for localizing the mobile users which is very important in traffic control and for rescue operations in emergency situations. A proposed technique for location determination will be discussed based on high resolution DOA technique such as MUSIC algorithm [12] which will provide good accuracy comparable to Global Positioning System (GPS) for mobile users without GPS receivers. In addition, the DOAs of the mobile stations form a location data bank that can be useful for system adaptation and reconfiguration for proper cellular design.

The paper is organized as follows: section II displays the geometry of the SP system while section III introduces the DOA estimation technique used for positioning the mobile users. In section IV, the DOA SP system is examined and evaluated for several scenarios and finally, section V concludes the paper.

• II.    Stratospheric cellular system

As shown in Fig. 1, the 3 dB contour of a beam directed towards(θ, ∅ ) from SP station. The direction of the beam and its beamwidths form the basic parameters that affect its footprint. Relating the cell location with the elevation angle is practically very important, therefore, it is advantageous to express the coverage area in terms of the beam pointing directions or elevation angles. Assuming that the elevation angle at the cell center is denoted by ε, it can be related by the beam pointing direction, θ , by the following approximate relation as shown in Fig.1:

ε=90-θ

In most SPs communications applications, the minimum elevation angle of 15 degrees is acceptable to avoid excessive scattering at lower elevation angles. The radius of coverage at this angle will be approximately 75 km.

The cell can be described by its dimensions i.e. in terms of its major and minor axes given by:

be =  (sin-1((1+-R)sin(90-£ +4))- sin-1((1+-R)sin(90-£ -4))-Be )           (2)

and de=2ℎsec(90-s)tan( ∅)          (3)

Where R is the earth’s radius which is about 6375 km, h is the platform altitude in km and B0 and В∅ are the beamwidths in θ and ∅ directions respectively.

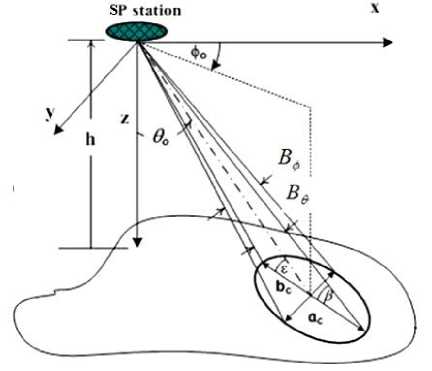
Fig 1: Footprint of a HAP cell

If the SP has localized in a point of ( X^p , y_SP ) which is considered as the origin point of the SP system, then the location of any MS, ( ^XMS , Уме ), relative to this origin can be determined from the DOA angles of this MS ( 6ms ^, Vms ) as follows:

^xms = sin( 9ms ^, Vms ) cos( 9ms ^, Vms ) (4) and

Vms = sin( 9ms ^, Vms ) sin( 9ms ^, Vms ) (5) where D is the slant distance between SP and MS given by:

D =ℎ / cos ( 9ms ) (6)

For each SP in the system, the set of ( ^xms , УМ5 ) for MSs forms a bank of location information that can be useful in many location-dependent services and many applications. The following section introduces the DOA estimation technique based on MUSIC algorithm which will define the set of ( 9ms , Vms ) of the served MSs.

• III.    The proposed directional-of-arrival technique

FOR SP MOBILE STATIONS

The estimation of the source angular components (i.e. azimuth and elevation) requires a planar array including the two-orthogonal uniform linear array (the L-shaped array) [12], the rectangular array [13], and the uniform circular array (UCA) [14-18]. Among these array structures, the UCA has gained attention due to its symmetry in detecting angles over 360 degrees in the azimuth plane [19]. The problem of estimating twodimensional direction-of-arrival (2D-DOA), namely azimuth and elevation angles of multiple sources have received considerable attention in the field of array processing [20-30]. Compared with the one-dimensional DOA, the 2D-DOA requires extensive calculations and the complexity depends on both the algorithm used and the array configuration. The maximum likelihood estimator [31] provides optimum parameter estimation; however, its computational complexity is extremely high. On the other hand, suboptimal solutions can be achieved by the subspace-based approach, which relies on the decomposition of the observation space into signal subspace and noise subspace. However, conventional subspace techniques for 2-D DOA estimation such as MUSIC [32] necessitate eigen decomposition of the sample covariance matrix or the singular value decomposition of the data matrix to estimate the signal and noise subspaces, and huge computation will be involved particularly when the dimensions of the underlying matrices are large. The use of circular arrays for MUSIC 2D-DOA has been addressed [33] but the search process for the impinging signals is performed in all available values of the elevation and azimuth angles which indicate a huge computational burden to accomplish the process and can be considered as blind 2D-DOA estimation technique. Therefore, in this paper we propose a novel search for fast and computationally efficient 2D-DOA estimation using MUSIC algorithm. This array is composed of uniform circular array (UCA)

Therefore, the 2D-DOA is performed sequentially and this will reduce greatly the required huge computations compared to the case when utilizing only the UCA especially for large array sizes and large number of sources.

The DOAs in the proposed algorithm will be searched with large angular separation which means less search points. If the DOA spectrum has some peaks, the algorithm will search again but over a zoomed area containing these peaks to resolve the sources with high accuracy. The process will continue until no new sources are detected with the highest number of the search angles.

The structure of the DOA beamformer is displayed in Fig. 2 where the array is UCA of N elements equally separated by half of wavelength distance.

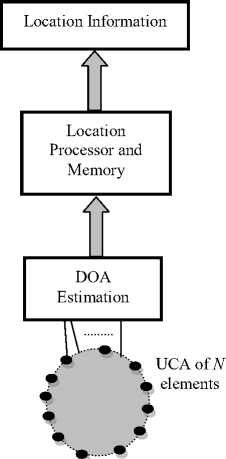
Fig 2: 2D-DOA SP System

For the circular array, the output signal is given by:

y (t)=W J X (t)             (7)

where W is the transpose of the circular array weights vector and X (t) is the array received signal vector given by:

X (t)=

[a (θ1,∅1)

^s (t) ⎢ ^s (t)

a ⁽ θ2,∅2) …a (θМ,∅М)]

+

⎣s М (t)⎦

n(t)

X (t)=A S(t)+n(t)          (9)

where a (θ1,∅1), a (θ2,∅2),… a (θм,∅м ) are the steering vectors of the circular array corresponding to the received signals, each of size N×1 , A is the array steering matrix and equals: [a (θ1,∅1) a (θ 2,∅2 ) … a (θМ,∅М)] with a size of N×M. The circular array steering vector at any direction θ is given by [24]:

a (θ,∅)

=[ej^sin ⁽⁸ )   (∅ N⁾ e j^sin ⁽⁰ )   (∅ n ⁾…ej^sin ⁽⁰ )   (∅-2Л ⁾ ]

where the interelement separation is taken as half of the wavelength.

The arriving signals are time-varying and calculations are based upon time snapshots of the incoming signal. Then, for any of the two arrays, the correlation matrix R XX is given by:

RXX =E[X Xн]               (11)

or

RXX =ARssAн+RNN         (12)

where RSS is M×M source correlation matrix, R ⁼ σnI is M×M noise matrix, I is N×N identity matrix and A is N×M array steering matrix.

The array steering matrix is basic in the following calculations needed for MUSIC 2D-DOA.

MUSIC is an acronym which stands for MUltiple Signal Classification which is an Eigen structure method. It depends on the properties of correlation matrix R XX where the space spanned by its Eigen vectors may be partitioned into two subspaces, namely the signal subspace and the noise subspace and the steering vectors corresponding to the directional sources are orthogonal to the noise subspace. This MUSIC approach is a simple, popular high resolution and efficient Eigen structure method. From array correlation matrix R XX we find M Eigen vectors associated with the signals and N-M Eigen vectors associated with the noise. Then choose the Eigen vectors associated with the smallest Eigen values. Noise Eigen vectors subspace of order N×(Ν-М) is constructed which is orthogonal to the array steering vectors at the angles of arrivals of the M sources.

For the UCA, the DOAs can be obtained from the peaks in the angular spectrum given by the MUSIC angular spectrum given by:

?MUSIC (6,∅)=   (e,∅) ^cN^cN^c(e,∅)| or

where   E_cN = [e ₁ e ₂... e_N __M ]  is Nx(N - M )  noise

Eigen vectors subspace from the circular array.

• IV.    Simulation results and discussion

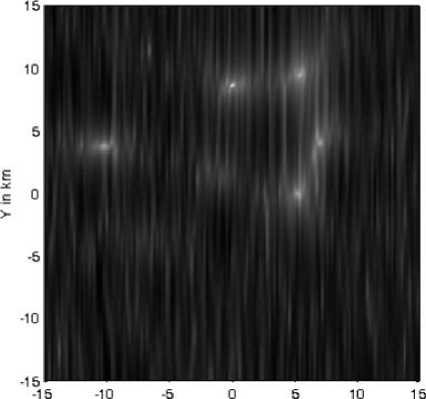
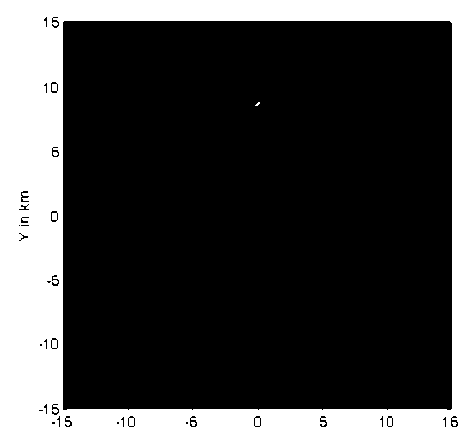
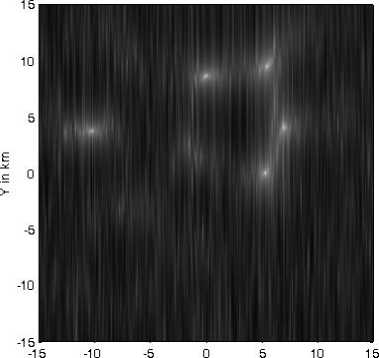
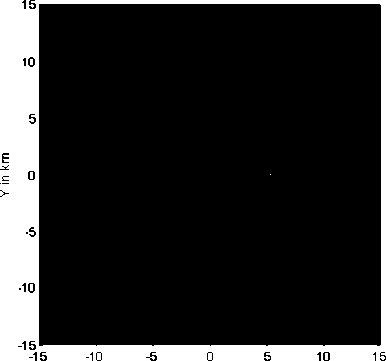
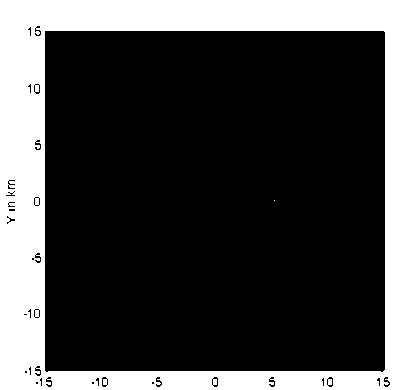
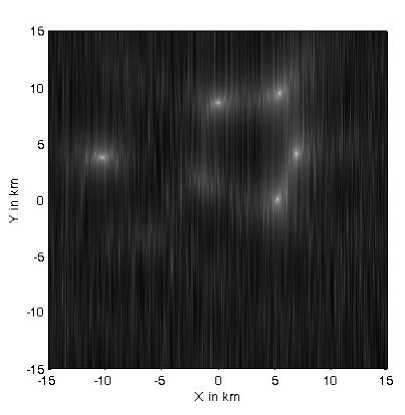
The location determination through DOA-MUSIC algorithm will be examined in this section. The array is composed of 30 omnidirectional antennas forming UCA. Assuming five MSs located at the following directions relative to the SP location point: (10o,0o), (15o,30o), (20o,60o), (16o,90o) and (20o,160o). Assuming line-of-sight propagation scenario between SP and MSs, therefore, the received signal from any MS will be constructed of one major strong line-of-sight component and other smaller amplitude scattered multipath signals. The effect of multipath components in the DOA calculations is supposed to be limited and may appear in the DOA spectrum as small amplitude peaks that can be neglected relative to a suitable threshold. The locations of the MSs are determined at different distance resolution which defines the complexity and time consumption in calculations. Starting with 200m resolution as shown in Fig. 3a, where the signal-to-noise ratio is assumed to be 30dB, the mobile stations give some peaks in the normalized DOA spectrum and due to the larger distance separation not all the MSs are detected. In Fig. 3b, the normalized DOA spectrum is filtered so that the points less than -20dB were cut to be -20dB. This chosen threshold will clarify the mobile locations and display it as points in the DOA spectrum with a clear black background. In Fig. 4a, the resolution is raised so that the distance separation is 100m. Other MSs peaks will appear after applying the threshold as in Fig. 4b but still with smaller peaks. If the resolution is increased as in Fig. 5a and 6a, the peaks in the DOA spectrum will appear clearly and Fig. 5b and 6b have clear points showing the location of the five MSs. The accuracy in detection is therefore dependent on the resolution of the DOA estimation and the price paid here is the increased time consumption in calculations due to the increased number of checked locations. To reduce the time consumption, one may start with lower resolution, and then increase this resolution until no new detected sources or MSs are obtained.

• V.    Conclusion

This paper has proposed a new technique for location determination of mobile stations using stratospheric platforms and directional-of-arrival estimation. The technique provides locations of mobiles stations with high accuracy without the need for GPS receiver at each mobile station. The DOAs can be mapped to an equivalent GPS coordinates or just locations relative to the SP location. The location information available in this system can be used for location dependent services and for rescue operations in emergency situations.

X in km

Fig 3a: Normalized DOA location spectrum for five MSs at 200m resolution

X in km

Fig 3b: Normalized DOA location spectrum for five MSs at 200m resolution at -20 dB floor

X in km

X in km

Fig 4a: Normalized DOA location spectrum for five MSs at 100m resolution

Fig 5b: Normalized DOA location spectrum for five MSs at 50m resolution at -20 dB floor

X in km

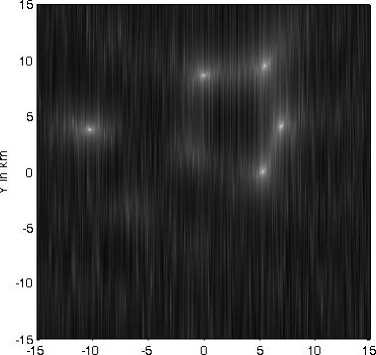
Fig 4b: Normalized DOA location spectrum for five MSs at 100m resolution at -20 dB floor

Fig 6a: Normalized DOA location spectrum for five MSs at 20m resolution

X in km

Fig 5a: Normalized DOA location spectrum for five MSs at 50m resolution

Fig 6b: Normalized DOA location spectrum for five MSs at 20m resolution at -20 dB floor