Discovery of Association Rules from University Admission System Data

Published Online May 2013 in MECS

Data mining aims at the discovery of useful information from large collection of data. Recently, there are increasing research interests in using data mining in education. This newly emerging field, called Educational Data Mining (EDM), concerns with developing methods that discover knowledge from data originating from educational environments [1].

Data mining techniques can discover useful information that can be used in formative evaluation to assist educators establish a pedagogical basis for decisions when designing or modifying an environment or teaching approach. The application of data mining in educational systems is an iterative cycle of hypothesis formation, testing, and refinement. As we can see in Fig. 1, educators and academics responsible are in charge of designing, planning, building and maintaining the educational systems. Different data mining techniques can be applied in order to discover useful knowledge that helps to improve both the academic and management processes [2].

Association rule mining is one of the major data mining techniques that interested in finding strong relationships and correlation among items in transactional databases. It can be employed in many areas including market analysis, decision support systems and financial forecast. An association rule has two measures: support and confidence that represent its statistical significance [3]. The problem of mining association rule is to discover the implication relation among items such that the presence of some items implies the presence of other items in the same transaction.

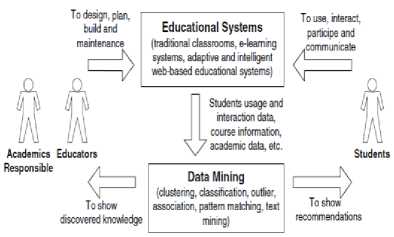
Figure 1. Data Mining Cycle in Educational System [2]

Mainly, all the proposed algorithms for association rules mining deals with transactional databases or market-basket data. These algorithms do not support relational databases naturally. To apply the same concepts and algorithms, relational database has to be converted to the transactional representation [4]. This requires the application of tedious conversion processes on large quantities of data before such algorithms can be applied as discussed with more details later in the paper.

In this paper, we aim to use current association rules mining techniques to handle university admission system. The current system is modeled as a relational database that require some preprocessing to be suitable for mining algorithms of association rules. We aim to help the admission office better understand the nature of the system and the parameters that affect the decision making policy for accepting or rejecting the incoming students’ applications.

The rest of this paper is organized into five sections. In section 2, the related work is presented. Section 3 contains, with brief details, the proposed association rules discovery model. In section 4, experimental results are stated and analyzed with respect to model results and admission system perspective. Finally, the conclusions of this work are presented in Section 5.

• II.    Related Work

Recently, some research studies were proposed to address the usage of data mining techniques in education especially in association rule mining.

Feng et al. Proposed a data mining model for university enrollment system. Their model contains two tasks; the first one was SOM clustering to group the Chinese provinces according to registration rate, first wish rate and Gross Domestic Product (GDP). The second task was to extract association rules from students’ collage choice, interests and the relevance of specialties to aid the management in making subspecialty enrollment scheme and sub-specialty enrollment propaganda [1].

Buldua et al. used association rules to discover the relation between the courses and the failed students. They apply the apriori algorithm on the data of students of Istanbul Eyup I.M.K.B. Vocational Commerce High School in which a list of failed courses was assigned to each student. Their model showed some important notes about the students’ performance in numerical courses to be adapted in the future [5].

Encheva et al. presented in [6] an association rule mining model to find correlations among students’ preliminary knowledge. Their target was to decide which specific knowledge students do not possess in order to start a new course successfully or to proceed with another section in a current subject. For each student, a list of test results was marked to evaluate the presented model. They utilized the same model to find the correlations among students’ preliminary knowledge in mathematics and their abilities to solve linear algebra related problems [7].

Abdullah et al. proposed a new measurement called Critical Relative Support (CRS) to mine critical least association rules from an educational context [8]. Least association rules are the association rules that consist of the least item. These rules are very important and critical since they can be used to detect the infrequent events and exceptional cases. The same authors also proposed a model to extract high correlation association rules. Their main objective was to examine enrollment data of omputer science students to find if this major matched with the students’ field interests or not [9].

Recently, Kumar et al. used association rules mining in discovering the factors that affect postgraduate study and assessment in Haryana University, India. They used data for some courses taught for postgraduate students to measure the students’ performance based on some factors like course instructor behavior, time schedule, curriculum design and students’ interests [10].

• III.    Association Rules Discovery

The association rules mining task are interested in extracting relations and correlation between items in market-basket data. In this format, the data contains several records called transactions, where each transaction is composed of some items as in Table I.

TABLE I. Transactional Database Example

ID	Items
1	A, B, D, E
2	B, C, E
3	A, B, D, E
4	A, B, C, E
5	A, B, C, D, E
6	B, C, D

The problem arises here is how to use the same algorithms to handle traditional relational databases where each record is composed of field values.

The association rules are represented as LHS → RHS, which means if the items in the LHS occurred then we can find the items in the RHS, which are called Boolean association rules. For example, a rule Tea → Sugar means that customers who bought tea tends to buy sugar also.

To determine the strength of an association rule, two measures are used; support and confidence. The support is the percentage of the database transactions that hold this rule and confidence measures the statistical significance of a rule. Consider rule A → B, the confidence of this rule can be calculated using (1).

support( A ∪ B )

confidence( A → B ) =                                  (1)

support( A )

There are two main steps to generate association rules:

• 1.    Find all frequent itemsets in the database.

• 2.    Generate association rules from frequent itemsets.

Finding all frequent itemsets is considered the main and challenging step of association rules discovery because it is computationally expensive. In other hand, generating association rules are straightforward step as illustrated later in this section.

• A.    KAU Admission System

King Abdulaziz University (KAU) admission system in the Kingdom of Saudi Arabia (KSA) is a complex decision process that goes beyond simply matching test scores and admission requirements because of many reasons. First, the university has many branches in KSA for both division male and female students. Second, there are huge numbers of applicants each year, which needs a complex selection criterion that depends on the high school study type, grades and applicant region/city.

In this paper, we are provided with samples from KAU system database that represent applicant student information and his/her status of being rejected or accepted to be enrolled in the university in three consecutive years (2010, 2011 and 2012). The database contains about 83K records, while each record represents an instance with 4 attributes and one class attribute that represents application status. Table II shows detailed information about each attribute in this database [11].

TABLE II Summary of Database Attributes

Attribute	Possible values
Students’ Gender (G)	•    Male (M) •    Female (F)
High School Study Type (HT)	•    Scientific Study (HT_S) •    Literature Study (HT_L) •    Unknown (HT U)
High School Grade (HG)	• A = mark > 85 • B = 75 > mark > 85 • C = 65 > mark > 75 • D = 50 > mark > 65
Area (A)	Code for student’s region city
Application Status (S)	•    Accepted •    Rejected

• B.    Preprocessing

The aim of the preprocessing step is to convert input database from its relational, tabular format into a transactional database format. In this process we simply assign some code for the possible values of each field, and then apply this coding scheme on the table to convert each record into a set of items as in marketbasket databases. Table III shows the coding scheme related to the possible values for each attribute in the admission database.

TABLE III Conversion Coding Scheme

Attribute	Coding Scheme
Students’ Gender (G)	•    Male (GM) •    Female (GF)
High School Study Type (HT)	•    Scientific Study (TS) •    Literature Study (TL) •    Unknown/Missing (TU)
High School Grade (HG)	• A => HA • B => HB • C => HC • D => HD
Area (A)	Axxxx (xxxx is area code)
Application Status (S)	•    Accepted (SA) •    Rejected (SR)

Tables IV and V contain example records from input database and its equivalent transactions using the above coding scheme.

TABLE IV. Example Input Database

G	HT	HG	A	S
M	HT_S	A	1007	Accepted
F	HT_L	B	1004	Rejected
F	HT_S	D	1004	Accepted
M	HT_U	B	1005	Rejected

TABLE V. Equivalent Transactional Database

ID	Items
1	GM, HS, HA, A1007, SA
2	GF, HL, HB, A1004, SR
3	GF, HS, HD, A1004, SA
4	GM, HU, HB, A1005, SR

As illustrated in the earlier, each record is transformed into a set of items based on the values of its fields. For example, the first record is for student with male gender, scientific study in high school, obtained a grade ‘A’, from area with code ‘A1003’ and accepted status. This record is transformed to transaction {GM, HS, HA, A1007 and SA} respectively.

• C.    Apriori Algorithm

The process of mining association rules consists of two steps: First, find all the frequent itemsets and secondly, generate the association rules from discovering frequent itemsets. The Apriori algorithm is the most well known algorithms for finding the frequent itemsets with candidate generation [12]. It is used for mining frequent itemsets for Boolean association rules. Many variations of the Apriori algorithm have been proposed that focus on improving the efficiency of the original algorithm.

The support of an itemset A is the percentage of transactions in the database that contain A. An itemset is frequent if the number of occurrences of that item is greater than or equal to a minimum support threshold min_supp.

Apriori algorithm starts by scanning the database to find all the items and count their support as candidates of size 1 (i.e. C 1 ) and removes infrequent items (count < mis_supp).

To generate candidates of size k+1, frequent itemsets from the previous pass are joined as C_k, = F_k x F_k . To improve the efficiency of the level-wise generation of frequent itemsets, an important property called the Apriori property is used to reduce the search space.

The Apriori property is based on the following observation. If an itemset S does not satisfy the minimum support threshold, min_supp , then S is not frequent. If an item A is added to the itemset S, then the resulting itemset (i.e. S u { A} ) Cannot occur more frequently than S and will be not frequent too [3].

So, the basic idea of the Apriori algorithm is to generate candidate itemsets of a particular size and then scan the database to count these to see if they are frequent. The candidates (C k ), of size k, are counted and only the frequent ones (F k ) are used to generate candidates for the next pass candidates (C k+1 ) until no frequent itemsets found as stated in the Apriori property.

For example, consider the dataset shown in table I. We need to apply the Apriori algorithm to find frequent itemsets with minimum support 60% (0.6 * 6 = 3.6), which means that the itemset is frequent if it is occurring in at least 4 transactions. Figure 2 shows the detailed algorithm steps.

The algorithm starts by scanning the items in the database and counting their support to remove the infrequent ones. To generate candidate-2 itemsets, the algorithm joins the items in F1 as they all share the same prefix class. The join operation between two itemsets L i and L j of size k is performed as follows: L i = {a 1 , a 2 , …., a k-1 , a k } and L j = {a 1 , a 2 , …., a k-1 , b k } can be joined to generate L ij = {{a 1 , a 2 , …., a k-1 , a k , b k } of size k+1. They must share the prefix class which is the itemset of k-1 items (i.e. {a₁, a₂, …., a_k-1} in this case), otherwise they cannot be joined.

For example, in F₂, only {AB} has prefix class {A}, so it cannot be joined with other F 2 itemsets. On the

Pass 1

other hand, {BC}, {BD} and {BE} have the same prefix class (which is {B}) so we can join each two of them to produce C 3 = {BCD}, {BCE} and {BDE}. The algorithm stops at this iteration because there are no F 3 itemsets.

• D.    Generating Association Rules

Once the frequent itemsets have been found from the transaction database, it is straightforward to generate the association rules for them. These rules must satisfy both minimum support and minimum confidence thresholds. Since the rules are generated from frequent itemsets, each one automatically satisfies minimum support.

The association rules are generated as follows:

• 1.    For each frequent itemset F, generate all the nonempty subsets of F.

• 2.    For every non-empty subset s of F, output the rule “ s → ( F - s )” if its confidence is greater than or equal min_conf threshold.

As an example, the frequent itemsets in Figure 2 will be used to generate output association rules as shown in with min_conf = 70%. F 1 itemsets are neglected because it contains only one item and will produce no rules. The generated rules that satisfy min_conf threshold are highlighted in Table VI.

Scan DB =>

C 1

count

==>

F 1

count

{A}

4

{A}

4

{B}

6

{B}

6

{C}

4

{C}

4

{D}

4

{D}

4

{E}

5

{E}

5

Pass 2: C 2

= F 1 x F 1

C 2

Scan DB ==>

C 2

count

{AB}

{AB}

4

{AC}

{AC}

2

{AD}

{AD}

3

==>

F 2

count

{AE}

{AE}

3

{AB}

4

{BC}

{BC}

4

{BC}

4

{BD}

{BD}

4

{BD}

4

{BE}

{BE}

5

{BE}

5

{CD}

{CD}

2

{CE}

{CE}

3

{DE}

{DE}

3

Pass 3: C 3

=

F 2 x F 2

C 3

Scan DB ==>

C 3

count

{BCD}

{BCD}

2

==>

F 3

count

{BCE}

{BCE}

3

{ }

{BDE}

{BDE}

3

Figure 2. Example of Apriori Algorithm

TABLE VI. Example Input Database

Frequent Itemset	Association Rules Confidence
{AB}	supp( AB )   4 A ^ B ,  -------- = — = 1.0 supp( A )   4
	supp( AB )   4 B ^ A ,  -------- = - = 0.67 supp( B )   6
{BC}	supp( BC )  4 B ^ C ,  ------- = - = 0.67 supp( B )   6
	supp( BC )  4 C ^ B ,            =  = 1.0 supp( C )   4
{BD}	supp( BD )  4 B ^ D ,  ------- = - = 0.67 supp( B )   6
	supp( BD )  4 D ^ B ,  ------- =- = 1.0 supp( D )   4
{BE}	supp( BE )   5 B ^ E ,  -------- = - = 0.83 supp( B )   6
	supp( BE )   5 E ^ B ,  ------- =- = 1.0 supp( E )   5

• IV.    Results and Discussion

• A.    Frequent Itemset

The entire database is processed to extract the association rules between the values of the input attributes. First, Apriori algorithm was applied to find all the frequent itemsets in the database with minimum support threshold min_supp = 40%. There are 11 frequent itemsets as shown in Table VII with their support value.

TABLE VII. Frequent Itemsets

Itemset	Supp. (%)
{A1007}	44.3
{GF}	61.0
{HA}	70.3
{TL}	77.6
{SA}	45.6
{SR}	54.4
{GF, HA}	40.0
{GF, TL}	54.5
{HA, SA}	40.7
{HA, TL}	57.3
{TL, SR}	43.4

We can notice that the majority of the applicants are females (about 61%), obtained ‘A’ grade in their high school (about 70%) and studied literature study (about 77%).

In spite of about 70% of the applicants holds ‘A’ grade in high school, only 40% of them were accepted to study in KAU, which means that the university accepts only the highest standard and very qualified students.

• B.    General Association Rules

As stated earlier, only size-2 frequent itemsets will be used to generate association rules. Table VIII shows the extracted association rules with min_supp =40% and min_conf =75% thresholds.

TABLE VIII. Generated Association Rules

Rule	Supp. (%)	Conf. (%)
SA ^ HA	40.7	89.4
SR ^ TL	43.4	79.7
GF ^ TL	54.5	89.3
HA ^ TL	57.3	81.5

There are four extracted association rules that have confidence not less than 75%, which means that they are very strong relations. From these rules, we can conclude the following:

• 1.    The accepted students have a high school grade ‘A’ with 89.4% confidence.

• 2.    The rejected students most likely were in literature study in their high school with 79.7% confidence.

• 3.    The female students most likely were in literature study in their high school with 89.3% confidence.

• 4.    Grade ‘A’ students most likely were in literature study in their high school with 81.5% confidence.

• C.    Classification Rules Induction

The database is classified into two classes with respect to application status. There are about 54.4% rejected (45K records) and 45.6% accepted (38K records) applications. We split the database is split into two parts based on the application status and apply the mining model separately to each part separately to find the relation between the values of the attributes and their class which gives a better understanding of the nature of the admission system.

TABLE VIII. “Rejected” Class – Association Rules

Rule	Supp. (%)
GF,TL ^ SR	62.7
GF ^ SR	70.8
TL ^ SR	79.7

Table IX shows the extracted association rules with thresholds min_supp =60% in case of rejected students, we can notice that:

• 1.    62.7% of the rejected students are females and studied literature study in high school.

• 2.    70.8% of the rejected students are females .

• 3.    79.7% of the rejected students studied literature study in their high school.

TABLE X. “Accepted” Class – Association Rules

Rule	Supp. (%)
HA, A1007 → SA	60.1
A1007 → SA	67.8
HA, TL → SA	68.4
TL → SA	75.2
HA → SA	89.4

Table X shows the extracted association rules with thresholds min_supp =60% in case of accepted students, we can notice that:

• 1.    60.1% of the accepted students are from ‘Jeddah’ city and obtained grade ‘A’ in high school.

• 2.    67.8% of the accepted students are from ‘Jeddah’ city.

• 3.    68.4% of the accepted students studied literature study and obtained grade ‘A’ in high school.

• 4.    75.2% of the accepted students studied literature study in high school.

• 5.    89.4% of the accepted students obtained grade ‘A’ in high school.

• V. Conclusion

In this paper, we presented an association rule discovery model to investigate and analyze KAU admission system database. The model discovered the relation students’ data and their application status in the university system. Mainly, most of the accepted students are from ‘Jeddah’ city, obtained a grade ‘A’ in their literature study in high school. Also, most of the rejected students are female students that have literature study in their high school. This information is very important to the admission office in KAU because it enhances their perspective to the admission system and shows how to filter the applicants with respect to their record in high school.

Another important point discovered from this work that state the class of students that KAU seeks. In spite of about 70% of the applicants holds ‘A’ grade in high school, only 40% of them were accepted to study in KAU. In addition, KAU admission office can use this information in adopting some advertisement strategies in other cities in the kingdom or offer some scholarships to excellent students to join the university.