Дискретизация непрерывных контуров изображений, заданных в комплекснозначном виде

Задачи контурного анализа возникают в системе технического зрения при обработке изображений и распознавании зрительных образов. Размер клетки (пикселя) сетчатки обычно выбирается из условия возможности восстановления исходного изображения по оцифрованному. Возникающие при этом ошибки дискретизации обусловлены наличием граничных пикселей, в пределах которых содержатся участки как фона, так и изображения объекта. Поэтому оцифрованное и исходное изображения не совпадают. Величина ошибки дискретизации зависит не только от размеров пикселя, но и от вида критерия принятия решения о принадлежности каждого из пикселей фону или изображению [1].

Для обработки контура аналитическим путём или на ЭВМ производят его кодирование, т.е. ставят в соответствие каждому контурному элементу определённое число. Контур Г , состоящий из элементарных векторов у ( n ), n = 0,1,..., s - 1, представляют в виде

Г = {y( n )}0, s-1 = {y( 0), Y(1) ’-, Y( s -1)}, где y(n) - элементарный вектор (ЭВ), соединяющий центры или узлы соседних контурных ячеек сетчатки. Такие ЭВ называют стандартными в отличие от ЭВ, длина и аргумент которых задаются произвольными числами. Стандартные элементарные векторы формируются естественным образом по введённому в ОЗУ изображению.

Полигональное представление контура получается при его аппроксимации линейными сегментами. Кодирование состоит в фиксации координат концов этих сегментов. Данный способ благодаря компактности получаемых описаний получил широкое распространение [1]. При этом возникает проблема сегментации, сходная с проблемой дискретизации сигналов. В реальных случаях она обычно связана с потерей информации о форме изображений. Таким образом, при представлении контуров изображений количество элементарных векторов определяется разрешающей способностью датчиков изображений. Как правило, такое представление является избыточным. Целью данной работы является исследование влияния дискретизации на качество распознавания контуров изображений.

1. Модель непрерывного контура

Контур X = { х ( 1 )} ₀, L как непрерывную замкнутую кривую, заданную на комплексной плоскости, представим в виде (рис. 1)

Х(1) = Xi(1) + i%2(1) = |%(1)| exP { iф(1)},1 е[0,2к], где Х1( 1) = Re х( 1) и х2( 1) = Im х( 1) - действительная и мнимая компоненты функции х(1).

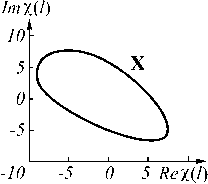
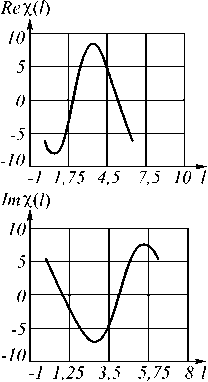
Рис. 1. Примеры непрерывных контуров изображений

При многократном обходе вдоль замкнутой кривой контур X можно представить в виде периодической функции с периодом 2 п , т.е. [2]

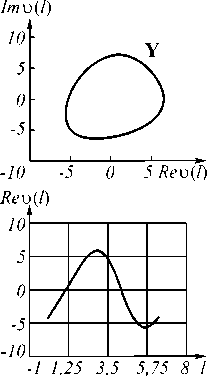
Im v(l)

-5

-10

-1 1,25 3,5 5,75 8 I

х ( 1 ) = х ( 1 + 2 па ), а = 0,1, 2,... .

Если х( 1) изменяется, подчиняясь тем или иным условиям, например X = {%(1 )}0,L задаёт контур изображения, то мы имеем дело с комплексной переменной, заданной на плоскости C комплексного переменного %. Представление контуров изображений в виде функции комплексного переменного позволяет привлечь для их анализа и обработки теорию функ- ции комплексного переменного. Так, например, частный случай дробно-линейного отображения: v = aY+ b, где a = a1 + ia2 и b = b1 + ib2, - произвольные комплексные числа, соответствует вращению на угол arga , растяжению в | a | раз и параллельному сдвигу на вектор b , служит для моделирования процесса формирования наблюдаемого контура X(c) путём растяжения исходного контура X в | ц | раз поворотом на угол Аф и сдвигом начальной точки на d ЭВ, т.е.

X(c) = { |ц||х(1 + d)|exp{ i[ф(1 + d) +Аф] }}    .

Зашумлённый непрерывный контур K = { к ( 1 )} 0 _{2 п} образуется как аддитивная смесь исходного X = ^{( х ^{1 )}} о,2п ^и реализации шумового Z = ^{ ^ ( l Яо^ контуров, т.е. к ( 1 ) = х ( 1 ) + Z ( 1 ), 1 = [0,2 п ]. Элемент к ( 1 ) является суммой постоянной составляющей детерминированной функции х ( 1 ) со случайной функцией Z ( 1 ), имеющей нулевое математическое ожидание, дисперсию D ^ и подчиняющейся нормальному закону распределения.

Практически все основные операции обработки контуров изображений используют для своей реализации базовую операцию – скалярное произведение принятого сигнала Y и эталонного – X :

L

(X,Y ) = f х( 1 )и* (1) d 1 = 0

L

= f (Х1 (1 )U1 (1 ) + Х2 (1 )U2 (1)) d 1 + 0

L

+if (Х2 (1 )U1 (1 )-Х1 (1 )U2 (1)) d 1. 0

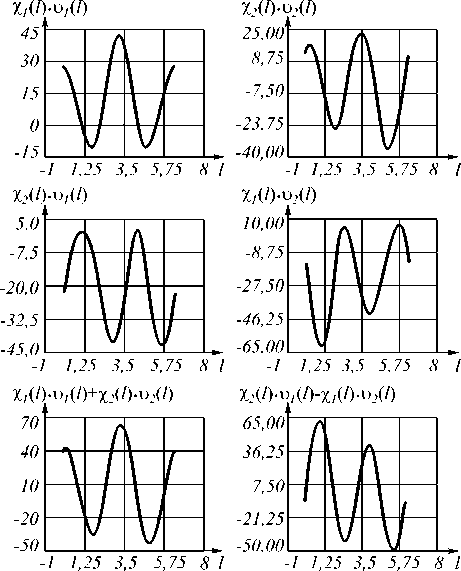
На рис. 2 представлены этапы вычисления скалярного произведения непрерывных контуров X и Y , показанных на рис. 1.

2. Дискретизация непрерывных контуров изображений

Если X = {х( 1 )}0,2п — произвольный контур, спектр P = {p(to)}      которого отличен от нуля в, в лишь в полосе частот -toв < to < toв, то его можно разложить в обобщённый ряд Фурье по базису Котельникова. С учётом комплекснозначного характера функции X , производим дискретизацию раздельно для действительной и мнимой частей. Получаем х (1) = Ё ci, n Scn (1;toв)+ic 2, n Scn (1;toв), n=-ю где ci,n = (х1 (1) , Scn (1; toв )) , c2,n = (х2 (1) , Scn (1; toв ))

– коэффициенты ряда. Причём величины c _{1, n} и c _{2, n} есть не что иное, как Y i ( n ) = х 1 ( 1_п ) и у 2 ( n ) = х 2 ( к ),

то есть мгновенные значения непрерывного контура х ( 1 ) в n -й отчётной точке 1 _n = ( n л)/to в .

jX2(/)-u₇(/)-x,(/).u₂(/) “16,780

jx/(0-u;(/)+x?(/)-u,(/) 39,150 39,125

16,767

39,100

39,075

39,050                    _

-10 -5 0   5 10 I

16,753

-10 -3,33 3,33 10 1

16,740

Рис. 2. Этапы формирования скалярного произведения непрерывных контуров X и Y , показанных на рис. 1

На рис. 3 представлен пример процесса дискре тизации непрерывного элементарного контура

^X m = ^{ х m ^{( 1} Ж^ = { | х | exP^{{ im1 }} } o,2n

порядка m = 1. Совокупность X m при m = -^ , ^ задаёт семейство замкнутых непрерывных элементарных контуров. При | х | = 1 любые два контура из полного семейства непрерывных элементарных контуров являются ортогональными, т.е. скалярное произведение контуров равно

L

( ^X m , ^X n ) = f ^exP { i ^{( m - n} ) ¹ } ^{d 1} =

2 п при m = n , 0 при m ^ n .

В результате дискретизации непрерывного элементарного контура X _i порядка m = 1 получаем дискретный элементарный контур Г ₁ порядка m = 1.

На рис. 4 представлены контуры Г , полученные путём дискретизации непрерывных контуров. При этом to в = 5 (рис. 4 а , в ) и to в = 10 (рис. 4 б , г ).

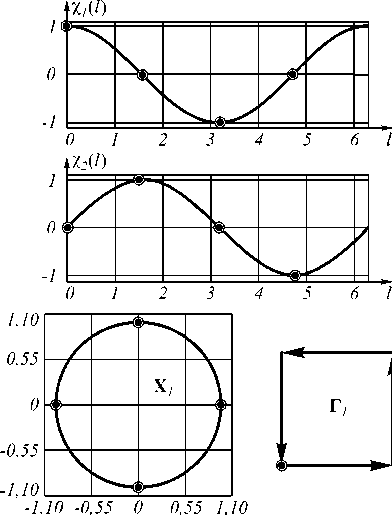
Рис. 3. Процесс дискретизации непрерывного элементарного контура X ₁

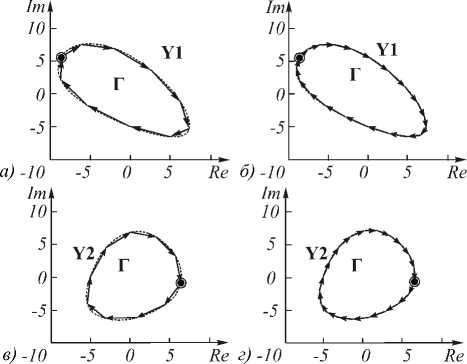
Рис. 4. Контуры Г , полученные путём дискретизации непрерывных контуров X и Y (см. рис. 1)

3. Исследование влияния дискретизации на распознавание непрерывных контуров изображений

Задача распознавания дискретных контуров изображений достаточно подробно рассмотрена в работах [1, 3]. В работе [4] решалась задача исследования потенциальной эффективности распознавания дискретных комплекснозначных векторных сигналов. В качестве меры различия двух сигналов было выбрано расстояние между задающими их векторами. Помехоустойчивость распознающей системы характеризовалась вероятностью правильного распознавания P_пр . Предполагалось, что величина P_пр одинакова для всех классов распознаваемых сигналов.

В [4] показано, что c практических позиций при обработке комплекснозначных сигналов значительно больший интерес для построения помехоустойчивых систем распознавания представляют семейства элементарных контуров, являющихся ортогональными сигналами. По эффективности распознавания они незначительно проигрывают симплексным сигналам. Однако получающиеся результаты распознавания инвариантны к линейным преобразованиям элементарных контуров, а различие в вероятностях Pпр по сравнению с симплексными контурами уменьшается с ростом размерности s .

Рассмотрим задачу распознавания зашумленных непрерывных контуров на примере двух классов. Пусть X ( 1 ) = ^{ Х (1) ( l ^)} 0, L и X (2) = ^{ % (2) ( l ^)} 0, L ^- непрерывные контуры, соответственно, классов A ₁ и A ₂ . На устройство распознавания подаётся либо зашумленный контур первого класса, равный K (1) = X ( 2 )) + Z , либо второго класса, равный K (₂₎ = Х (2) + Z , где Z — реализация шумового контура.

Задача распознавания состоит в обоснованном отнесении зашумлённого контура K к одному из классов – A ₁ или A ₂ . Для принятия решения необходимо сформировать безусловное отношение правдоподобия и сравнить его с пороговым значением. Функции правдоподобия контуров K ₍₁₎ и K ₍₂₎ имеют, соответственно, вид

^Л ( ^K , |^ ( 1 ) | , ^Аф ( 1 ) , d ( 1 ) ) =

)

= c • exp

/_ ¹ IIkII²— lx^{( c} )ll                X^{( c} )

I 2 5 U ^k H^x(1)II ^{2Re ( K X} ( 1 )

^Л ( ^K ,| M ( 2 )| ^{, А} * ( , ) ^, d ( 2 ) ) =

= c ^ ^eXP {" 21 [^{1 |K||!} — I IX ( c »Г — 2 Re ( ^{K ,} X ( C ) ) ] } .

Тогда логарифм условного отношения правдоподобия запишется как ln

L ( ^K , |Ц ( 1 )| , |Ц ( 2 )| , ^Аф ( 1 ) , ^Аф ( 2 ) , d ( 1 ) , d ( 2 ) )

• -      ¹ J k( c )|I²        ( c )|I²

• = - 25 2 ll |^X( 1 ) "I|^X( 2 ) "

• - 2 [ Re ( ^{K , X} ( c )) ) " Re ( ^{K , X} ( 2 1 ) ] } .

Если на вход распознающего устройства подаётся зашумлённый контур из некоторого алфавита объёмом M классов, то алгоритм распознавания предусматривает многоканальную по числу классов процедуру.

На рис. 5 приведены графики зависимости вероятности правильного распознавания Pпр зашумлённых непрерывных X m ={{X m (l )}}0,2n ={exp{Zml}}0,2n элементарных контуров от отношения сигнал/шум q при объёмах алфавита M = 5 , 10 и 15 .

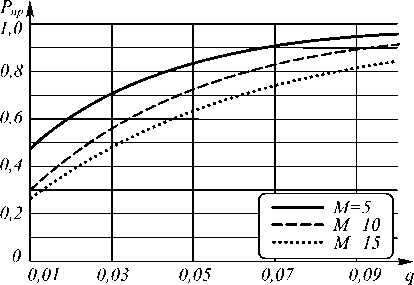
Рис. 5. Характеристики распознавания непрерывных элементарных контуров

Величина q равна отношению средней энергии || X _т| |²/2л элементарного вектора непрерывного элементарного контура X _m к дисперсии шумового контура Z : q = | |Х „ ||²/2ло ² .

Скалярное произведение двух непрерывных элементарных контуров X _m и X _n , являющихся ортогональными сигналами, равно нулю. Поэтому расстояние между нормированными непрерывными элементарными контурами постоянно. Снижение вероятности P_пр при распознавании зашумлённых непрерывных элементарных контуров, связанное с увеличением количества M классов, объясняется возрастанием количества параллельно работающих каналов, для каждого из которых может быть принято ошибочное решение о распознавании.

На рис. 6 приведены графики зависимости вероятности правильного распознавания P_пр от отношения сигнал/шум q для элементарных контуров, полученных путём дискретизации непрерывного эле-

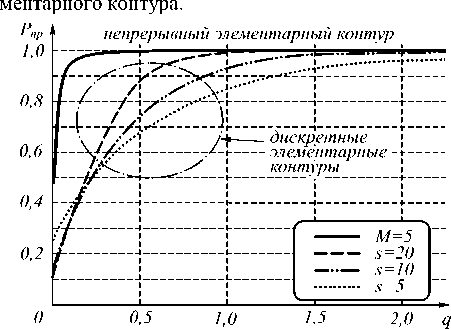
Рис. 6. Зависимость вероятности правильного распознавания от отношения сигнал/шум

С увеличением размерности дискретизированного элементарного контура кривая зависимости вероятности правильного распознавания от отношения сиг-нал/шум стремится к зависимости вероятности пра- вильного распознавания непрерывного контура. Однако при увеличении размерности контуров, очевидно, увеличивается и трудоёмкость их обработки.

Представленные на рис. 6 характеристики определяют потенциальную эффективность распознавания комплекснозначных сигналов и позволяют выбирать размерность сигнала для достижения требуемой вероятности правильного распознавания.

Заключение

В работе решена задача распознавания непрерывных контуров изображений. При этом считалось, что задан алфавит эталонных изображений всех классов. На устройство распознавания поступает зашумлённый непрерывный контур изображения одного из классов алфавита. Устройство распознавания выносит оптимальное по критерию минимального расстояния решение в пользу одного из классов алфавита. Основой устройства служит фильтр, согласованный с непрерывным контуром изображения одного из классов.

Исследовано влияние дискретизации на распознавание непрерывных контуров изображений. Построены сравнительные характеристики вероятности правильного распознавания непрерывных и дискретных элементарных контуров. Показано, что при увеличении отчётов дискретных контуров вероятность правильного распознавания увеличивается.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 11-07-00585-а).