Дискретная модель исследования потокообразующих факторов в системе поддержки принятия решений по управлению транспортными потоками

Существуют различные подходы к решению современных проблем дорожно-транспортного движения, важнейшим элементом которого являются транспортные потоки. Принятие решений по управлению транспортными потоками предполагает рассмотрение дороги с разных позиций — с позиции водителей, жителей населённого пункта, инвесторов и т.д. Поэтому решения по управлению транспортными потоками чаще всего принимаются не одним человеком, а группой лиц — лицами, принимающими решение (ЛПР). Обычно в группу ЛПР входят специалисты из разных отраслей — строители, автомобилисты, чиновники, сотрудники ГИБДД и т.п. Каждый из числа ЛПР руководствуется своими критериями эффективности принимаемого решения [5].

Сложность решения в задаче управления транспортными потоками связана с тем, что далеко не все характеристики исследуемого участка дороги можно однозначно представить математически. Вообще, задача принятия решений по управлению транспортными потоками является трудно формализуемой. Кроме того, зависимости между критериями могут быть нетривиальны.

Решение подобных задач сводится к комплексному исследованию множества решений на основе различных инструментариев, образующих систему поддержки принятия решений.

Компьютерные системы поддержки принятия решений (КСППР) (Decision Support System, DSS) — особый класс автоматизированных систем, обеспечивающих оказание человеку помощи в принятии решений в сложных условиях, путём объективного исследования предметной области. КСППР не заменяют человека, а лишь помогают ему проанализировать предметную область и выявить множество возможных решений задачи. Что же касается выбора решения — это остаётся за человеком [1, 5].

КСППР обеспечивают исследование предметной области различными методами [1, 5]:

оптимизация некоторой целевой функции (нахождением её экстремумов), определяемой некоторым множеством критериев;

• •    поиск в базе знаний, содержащей некоторые оценки экспертов;

• •    моделирование.

Также КСППР, могут использовать и другие методы. Например, элементы искусственного интеллекта, нейронные сети и т.д.

Важной особенностью КСППР является поддержка удалённой работы в многопользовательском режиме, что предполагает использование современных сетевых технологий и клиент-серверной архитектуры.

Современные системы поддержки принятия решений по управлению транспортными потоками позволяют с разных позиций исследовать систему ВАДС (Водитель — Автомобиль — Дорога — Среда ). Благодаря использованию компьютерных систем поддержки принятия решений могут быть получены различные оценки дорожного движения, помогающие принимать управленческие решения [2, 4].

Немаловажную роль в СППР играют различные инструментарии оценки и выработки управленческих решений на дискретных структурах (потоки в сетях, графовые модели, нейросетевые модели, сети Петри и др.). Данные инструментарии позволяют получить различные варианты альтернативных решений по организации движения транспортных потоков, каждый из которых можно оценить используя имитационное моделирование [1, 4, 5].

Итак, КСППР позволяет оценить различные подходы к организации движения транспортных потоков — установку дорожных знаков, организацию различных типов пешеходных переходов, строительство транспортных развязок и дорог, организацию платного проезда и др. Каждый конкретный путь решения имеет свои преимущества и недостатки и в одних ситуациях может быть эффективно применён для организации движения транспортных потоков, а в других случаях только затруднить дорожное движение.

В условиях современных мегаполисов наблюдается существенная нехватка площадей для строительства, а также высокая плотность населения и большая численность транспортных средств. В таких условиях строительство новых автомобильных дорог часто является невозможным. Организация надземных и подземных переходов направлена в основном на решение проблем безопасности пешеходов, но не решает проблемы перегруженности дорожной сети.

Стоит заметить, что современная специфика работы предприятий мегаполисов заключается в том, что их рабочий день начинается в одно и то же время и заканчивается в одно и то же время, следовательно возникают часы-пик. Однако, в часы-пик в основном наблюдается движение только в одном направлении. Также стоит заметить, что в остальное время численность транспортных средств на дорогах достаточно мала. Поэтому, в качестве одного из путей решения проблем, связанных с организацией движения транспортных потоков можно рассматривать перераспределение транспортных потоков в течение суток. Фактически, необходимо устранить часы-пик и добиться более равномерного использования дорожной сети.

По сути, для каждого предприятия нужно будет определить время, в которое его сотрудники должны ехать на работу/уезжать с работы. Очевидно, что сотрудники ряда предприятий не должны будут одновременно использовать дороги. Для выражения этого факта построим граф G=

, носителем которого является множество предприятий:

P ={ P 1, P 2, ... ,P n } .

Сигнатурой графа являются пары предприятий, которые не должны одновременно пользоваться дорожной сетью:

V ={ V 1,V2,...,Vm }

V k = tP^P jQ iJ = 1,2 , ... ,N;k = 1,2 , ... ,M

Тогда для данного графа можно найти множество раскрасок вершин графа G=

, т.е. разбиение носителя P на подмножества, при котором каждое подмножество

• P, U Pi= P; Pi.П Pi. = 0 ; ia, ib = 1,2,..., t С i = 1

не содержит ни одной пары смежных вершин [3].

Каждое множество соцветных вершин P i представляет собой предприятия, одновременно использующие дорожную сеть.

Таким образом, предложена предметная интерпретация раскраски графов. Каждая раскраска представляет собой решение по организации рабочего времени на предприятиях. Каждый цвет в раскраске — это множество предприятий, которые используют дорожную сеть в одно и то же время. Причём речь идёт о любом использовании, как о проезде на работу/с работы сотрудников предприятий, так и доставки сырья, полуфабрикатов и т.п. Фактически каждый цвет может соответствовать некоторому интервалу времени, и количество таких интервалов будет ограничено, поскольку в зависимости от конкретного населённого пункта может отличаться время проезда к месту работы. Поэтому, требуется раскрасить граф в определённое количество красок L , соответствующих периодам времени использования дорог. Исходя из этого, можно выявить запрещённые фигуры, не позволяющие раскрасить описанный граф G= в требуемое количество красок L. Таковыми являются полные подграфы:

FL с G

и квазиполные подграфы квазиплотности L [3]:

P L,kсG .

Наличие таких запрещённых фигур показывает невозможность распределения движения транспортных средств в течение суток и требует применение других мер по организации движения.

Итак, выше была рассмотрена предметная интерпретация раскраски графа, определяющего невозможность одновременного использования дорожной сети несколькими предприятиями. Как видно, данный подход сводится к построению графовой модели, отражающей специфику использования дорожной сети. Однако, наибольший интерес представляет именно построение такой модели. Здесь может быть рассмотрено несколько подходов.

Построение модели определяется следующими особенностями:

расположение предприятия. Считаем, что большинство предприятий расположено в центре мегаполиса, куда съезжаются все сотрудники, создавая заторы на дорогах;

численность транспортных средств на предприятии;

направление движения к предприятию/ от предприятия. Возможно, что большинство работников едут только с конкретной стороны (например, с юго-востока), а значит используют только часть элементов дорожной сети;

зависимость предприятий друг от друга.

Здесь приведено несколько наиболее существенных факторов, влияющих на распределение транспортных потоков. Каждый из них можно так или иначе учитывать при построении графовой модели.

Рассмотрим самый простой вариант, когда между предприятиями нет зависимости, или зависимостью можно пренебречь. Такая ситуация достаточно распространена в случае, если предприятия относятся к сфере услуг, полностью производят продукцию в одном и том же месте (предприятия полного цикла). В этом случае функционирование предприятий не зависит друг от друга и всё определяется только численностью транспортных средств на каждом из них. Пусть имеем множество предприятий:

P ={ P i, P 2,... ,PN } на которых есть соответствующие количества транспортных средств, на которых сотрудники добираются на работу:

^Q =^{ q i, q 2, ... ,q N ^} .

Два множества P и Q задают носитель взвешенного ориентированного графа, который может быть разбит на подмножества так, чтобы их мощности были бы максимально близки по значению, т.е.

Q'^ Q;

|Ф OQ' i &  P OQ' j [фП 0 ; V i, j *

Очевидно, что при отсутствии зависимости предприятий друг от друга, граф G=

является пустым, т.е. G=

, тогда он может быть раскрашен в L красок, где L=1,2,...,N . Однако, в этом случае, на L накладываются эвристические ограничения, связанные с невозможностью работы в ночное время и т.п..

Например, имеем 10 предприятий, на которых соответственно Q={21,33,18,13,24,31,2 7,42,20,16}, тогда если каждое предприятие работает с 9:00 до 18:00, а время проезда до места работы 1 час, то в периоды с 8:00 до 9:00 и с 18:00 до 19:00 на дороге будет находиться 246 транспортных средств.

При этом всё остальное время дороги пустуют. Однако, сдвигая график работы всего на 1-2 часа, удаётся существенно снизить количество транспортных средств на участке дороги. На рис.1 приведены таблицы, иллюстрирующие две раскраски, показывающие распределение рабочего графика на 2 и на 4 временных интервала.

Как видно, такой подход позволяет существенно снизить количество транспортных средств, находящихся одновременно на дороге.

Другие варианты применения данного подхода предполагают построение графа на основе различных правил и критериев, которые определяются экспертами. При построении такого графа можно также руководствоваться статистикой использования отдельных участков автомобильных дорог транспортными средствами, связанными с предприятиями.

Прежде всего стоит рассмотреть вопрос зависимости предприятий. Речь идёт о так называемой «логистической» зависимости, при которой предприятия выполняют какие-либо этапы производства продукции и реализацию продукции: доставку сырья, выпуск полуфабрикатов, складирование, сбыт и т.п.

Множества		С1   С2                                             С1   С2
к х н о; О. С Ч Ф О. с	22			22										22
	33			33										33
	18			18										18
	13			13										13
	24				24										24
	31				31										31
	27				27										27
	42				42										42
	20			20										20
	16			16										16
Кол-во ТС		0	0	122	124	0	0	0	0	0	0	0	0	122	124	0	0
Время      1		6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21

Множества		С1   С2   С3  С4                                 С1   С2  С3   С4
X н X о. с Ч Ф О. с	22			22										22
	33		33										33
	18			18										18
	13		13										13
	24					24										24
	31					31										31
	27				27										27
	42				42										42
	20			20										20
	16		16										16
Кол-во ТС		0	62	60	69	55	0	0	0	0	0	0	62	60	69	55	0
Время      1		6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21

Рис. 1.

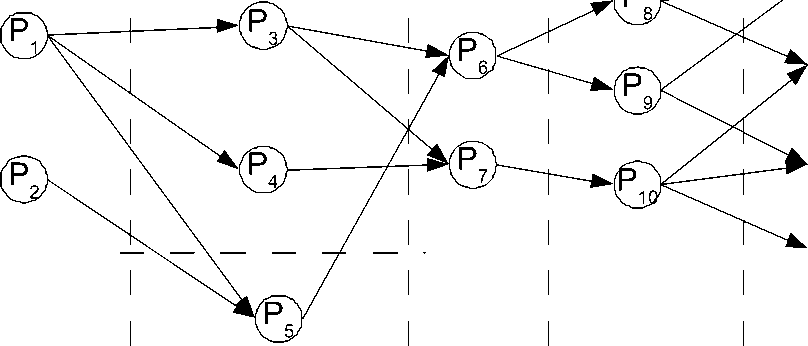
Тогда все предприятия на различных этапах производства можно будет ярусно упорядочить, в соответствии с этапами производства и зависимостью от времени (рис. 2). Такая модель показывает логистическую зависимость, между предприятиями, а также временную зависимость их работы. Как видно, модель имеет вид посета (частично упорядоченного множества). Также, стоит учесть время перевозки сырья, полуфабрикатов и товаров на этой модели. Здесь временем перевозки может быть взвешено каждое ребро. Тогда появляется возможность для каждого предприятия определить время использования им дорожной сети. Кроме того, стоит учитывать циклический характер работы некоторых предприятий (например, осуществляющих доставку сырья).

По модели (рис. 2) может быть построен граф противоречий, исходя из следующих правил:

• •    Предприятия на одном ярусе не работают параллельно (есть ребро в синтезируемом графе), если от их деятельности зависят дальнейшие этапы производства (предприятия следующего яруса), например P 3 и P 5 ; P 4 и P 5 , поскольку от них соответственно зависят P 6 и P 7 .

• •    Предприятия на соседних ярусах не зависимы (соединяются ребром) только в случае, если между ними установлена связь на исходной модели.

  Доставка	Изготовление Сборка	Склади-	1 m Продажа
  сырья	Полуфа-      1         1	рование	1

бриката2

ИзготовлениеПолуфа-бриката1

Рис. 2.

В отдельных случаях ребро может не устанавливаться, например, когда фактически зависимости нет. Например, один магазин может снабжаться несколькими складами, и если с одного склада готовую продукцию не привезут, производство не нарушится.

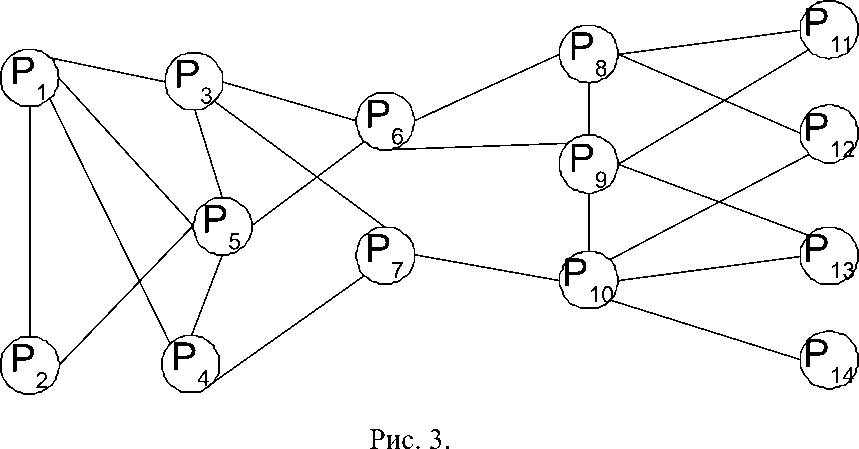
В полученном графе вершины, соответствующие предприятиям соединяются в случае, если они могут использовать дорожную сеть в разное время (Рис. 2). Порождая раскраски данного графа, можно получить множество способов организации рабочего времени предприятий. Каждое решение предполагает также наличие на дорогах определённого количества транспортных средств, связанных с каждым предприятием (так что по сути полученный граф является взвешенным). Поэтому, каждую раскраску необходимо также оценить и с этой точки зрения.

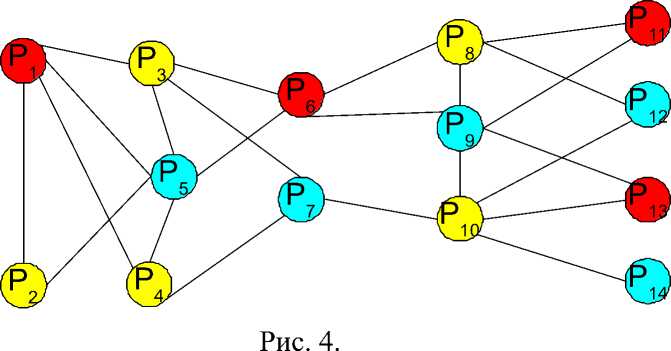
Возьмём для примера одну раскраску (рис. 4) и рассмотрим её для случая, когда на всех предприятиях равное количество транспортных средств. Тогда, необходимо разбить носитель равномерно. В результате применения минимальной раскраски, получаем три временных интервала, в каждый из которых до работы будет добираться только часть сотрудников. Как видно из рис. 5, такой способ реорганизации рабочего времени позволил сократить нагрузку в часы-пик почти в три раза.

Множества

YRC          YRC

к 1-к о. 5 О. с

P1

10

П

2

П

2

П

2

П

2

П

10

P2

10

П

2

П

2

П

2

П

2

П

10

P3

10

П

П

П

П

П

П

П

П

П

10

P4

10

П

П

П

П

П

П

П

П

П

10

P5

10

П

П

П

П

П

П

П

П

П

10

P6

10

П

П

П

П

П

П

П

П

П

10

P7

10

П

П

П

П

П

П

П

П

П

10

P8

10

П

П

П

П

П

П

П

П

П

10

P9

10

П

П

П

П

П

П

П

П

П

10

P10

10

П

П

П

П

П

П

П

П

П

10

P11

10

П

П

П

П

П

П

П

П

П

10

P12

10

П

П

П

П

П

П

П

П

П

10

P13

10

П

П

П

П

П

П

П

П

П

10

P14

10

П

П

П

П

П

П

П

П

П

10

Кол-во ТС

0

50

40

52

2

2

2

2

2

2

2

50

40

50

0

0

Время

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

Рис. 5

Итак, был рассмотрен инструментарий выработки решения по управлению транспортными потоками, в основе которого лежит их рассмотрение с позиции потокообразующих факторов. Предложенный подход может быть усовершенствован с возможностью учёта различных критериев, определяемых экспертами.