Дискретность магнитных моментов однодоменных ферромагнитных наночастиц

В процессе получения ферромагнитных наночастиц методом химической конденсации размер наночастицы постепенно возрастает, а магнитный момент Р у наночастицы появляется скачком, когда ее размер достигает нескольких нанометров и она становится доменом. Так как магнитный момент не квантуется, его скачкообразное изменение можно объяснить квантованием какой-то другой связанной с ним магнитной величины. Единственной магнитной величиной, квантование которой наблюдается на опыте, является магнитный поток Ф, имеющий квант f = ( ћ / 2 е ) = 2.065× ×10^–15 Тл. Найдем связь между Р и Ф.

СВЯЗЬ МЕЖДУ МАГНИТНЫМ МОМЕНТОМ ФЕРРОМАГНИТНОЙ НАНОЧАСТИЦЫ И СОЗДАВАЕМЫМ ЕЮ МАГНИТНЫМ

ПОТОКОМ

Связь между магнитным потоком и магнитным моментом найдем на примере соленоида с цилиндрической обмоткой длиной L , площадью сечения S и числом витков N , по которой протекает ток I . Магнитный момент такого соленоида Р = I N S , а магнитный поток Ф = I N S µ 0 / L . При этом

Р = (Ф L / µ 0 ).                  (1)

Таким образом, если наночастицу представить в виде цилиндра с постоянной эффективной длиной L, то квантование создаваемого ею магнитного потока должно приводить к дискретности ее магнитного момента. Естественно предположить, магнитный момент, магнитный поток, квант что наночастица с минимальным наблюдающимся на опыте магнитным моментом, равным шагу дискретности магнитного момента ∆Р, создает минимальный магнитный поток Фмин = f. Исходя из этого, зная ∆Р, можно оценить эффективную длину кванта магнитного потока:

L f = (∆ Р µ 0 / f ).                    (2)

ОПРЕДЕЛЕНИЕ ШАГА ДИСКРЕТНОСТИ ∆ Р МАГНИТНОГО МОМЕНТА ОДНОДОМЕННЫХ

НАНОЧАСТИЦ ПО ИК-СПЕКТРУ

ПОГЛОЩЕНИЯ МАГНИТНОЙ ЖИДКОСТИ

На рис. 1 приведены полученные на спектрометре Perkin Elmer, имеющем диапазон волновых чисел от 10³ см^–1 до 5·10³ см^–1, ИК-спектры поглощения коллоидного раствора наночастиц магнетита в керосине (магнитной жидкости), помещенного в магнитное поле с индукциями В = 0 (кривая 1), В = 0.075 Тл (кривая 2) и В = 0.085 Тл (кривая 3). На кривой 2 видны две линии поглощения(обозначим их "а" и "b") при резонансных волновых числах k а = 1550 см^–1, k b = 2050 см^–1, на кривой 3 видны две линии поглощения (обозначим их "а*", "b*") при резонансных волновых числах k а* = 1650 см^–1, k b* = 2250 см^–1. Эти же спектры приведены в предыдущей нашей работе [1], где поглощение ИК-излучения магнитной жидкостью объяснено эффектом магнитного резонанса наночастиц, а присутствие двух линий объяснено вызванным межчастичным взаимодействием сдвигом локального магнитного поля внутри конгломератов наночастиц. В настоящей

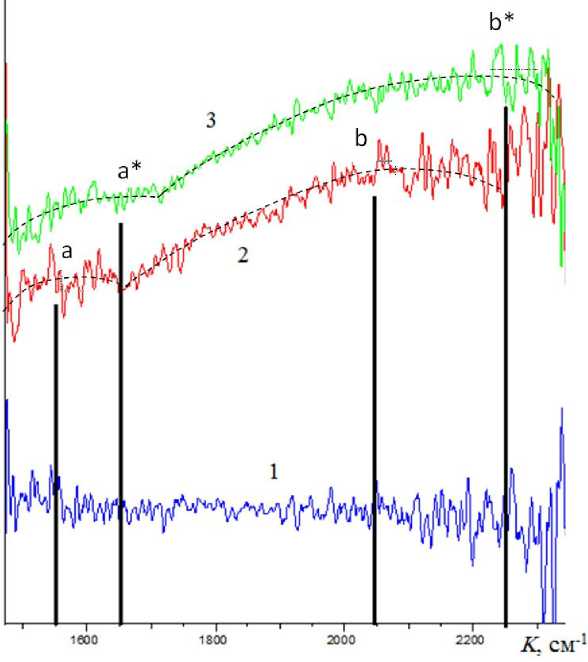
Рис. 1. ИК-спектр поглощения магнитной жидкости во внешнем магнитном поле с индукцией В .

Кривая 1 — при В = 0 Тл, кривая 2 — при

В = 0.075 Тл, кривая 3 — при В = 0.085 Тл работе появление двух линий объясняется иначе. Предлагается гипотеза о дискретности магнитных моментов наночастиц, согласно которой в ИК-спектре поглощения магнитной жидкости присутствуют отдельные линии резонансного поглощения, создаваемые наночастицами, содержащими одинаковые количества(1, 2, 3 и т. д.) квантов магнитного потока и поэтому имеющих одинаковые дискретные магнитные моменты. Отношения указанных вертикальными линиями резонансных волновых чисел пиков "b" и "а" на кривой 2 (kb / ka) = (2050 / 1550) = 1.32 и пиков "b*" и "а*" на кривой 3 (kb* / ka*) = (2250 / 1650) = 1.36. Эти отношения близки к числу 1.33 = (4/3), поэтому можно предположить, что пики "а" и "а*" получены от наночастиц, содержащих 3, а пики "b" и "b*" от наночастиц, содержащих 4 кванта магнитного потока, т. е. kа = k3 = 1550 см–1, kb = k4 = 2050 см–1, kа* = k3* = 1650 см–1, kb* = k4* = 2250 см–1. Исходя из этого можно найти выходящие за пределы диапазона ИК-спектрометра Perkin Elmer резонансные волновые числа первого и второго пиков, полученных от наночастиц, содержащих 1 и 2 кванта магнитного потока, на кривой 2 (k1, k2) и на кривой 3 (k1*, k2*): k1 = (k3/ 3) = (1550 / 3) = 517, или k1 = (k4 / 4) = (2050 / 4) = 513 (в среднем k1 = = 515 см–1), k2 = 2k1 = 1030 см–1, k1*= (k3*/ 3) = = (1650 / 3) = 550, или k1* = (k4* / 4) = (2250 / 4) = = 562 (в среднем k1* = 556 см–1), k2* = 2k1* = = 1112 см–1. По волновым числам k1, k1* найдем минимальные магнитные моменты:

Р 1 = ( h с k 1 / 2 В ) = (6.6·10^–34·3·10⁸·5.15·10⁴ / 2 × × 0.075) = 6.8·10^–20А·м²

и

Р 1* = ( h с k 1* / 2 В ) = (6.6·10^–34·10⁸·5.56·10⁴ / 2× × 0.085) = 6.47·10^–20А·м².

Полученное среднее значение минимального магнитного момента Р ₁ = 6.6·10^–20 А·м² можно принять за шаг дискретности магнитного момента наночастицы ∆ Р . Подставив ∆ Р = 6.6·10^–20 А·м² в выражение (2), находим эффективную длину кванта магнитного потока

L f =

=(∆Р µ0/ f) = (6.6·10–19·4π·10–7/ 2·10–15) ≈ 0.4·10–10м, близкую к радиусу первой орбиты электрона в атоме водорода.

У. е.

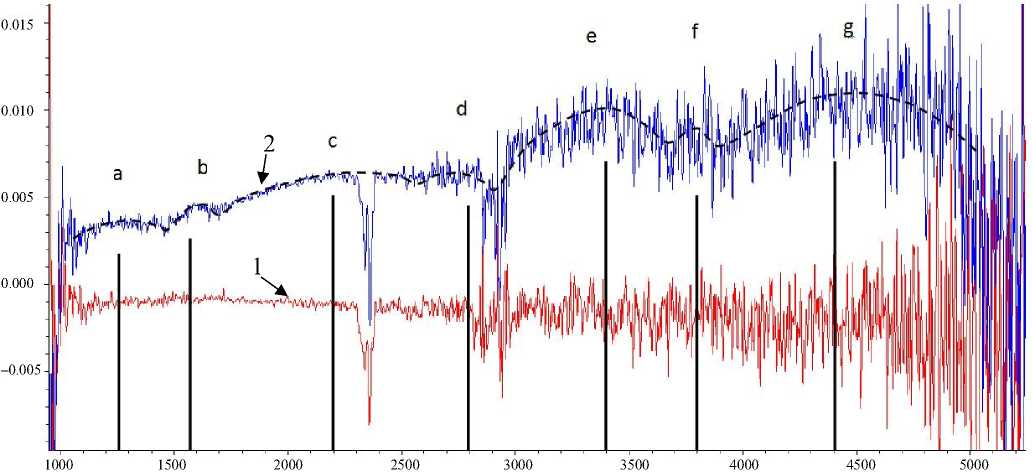
Рис. 2. ИК-спектр поглощения магнитной жидкости в магнитном поле с индукцией В.

K , см^–1

Кривая 1 — при В = 0, кривая 2 — при В = 0.03 Тл

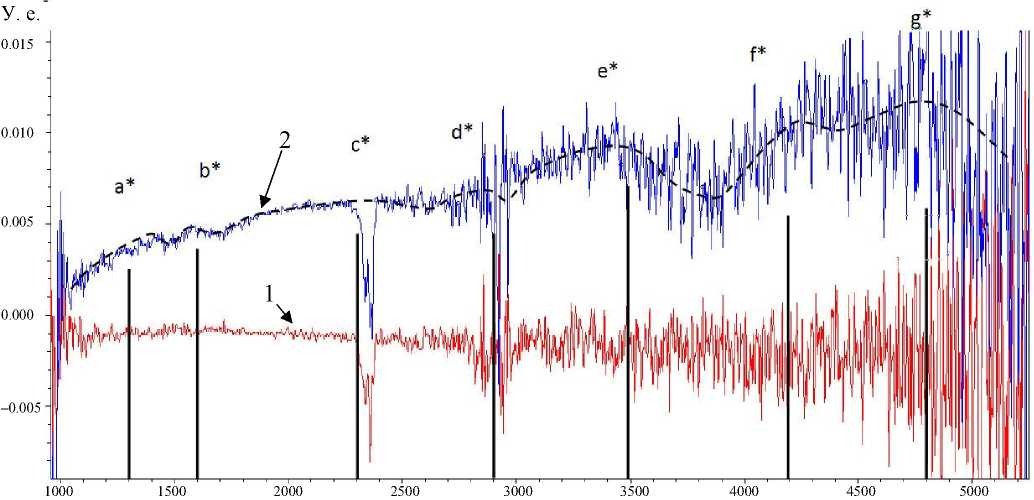
K , см^–1

Рис. 3. ИК-спектр поглощения магнитной жидкости в магнитном поле с индукцией В. Кривая 1 — при В = 0, кривая 2 — при В = 0.035 Тл

На рис. 2 и 3 приведены ИК-спектры поглощения той же магнитной жидкости в магнитных полях с индукциями В = 0.03 Тл (рис. 2) и В = 0.035 Тл (рис. 3). На этих спектрах видны линии поглощения, обозначенные латинскими бук- вами а, b, с, d, е, f, g. Резонансные волновые числа этих линий: на рис. 2: kа = 1250 см–1, kb = = 1570 см–1, kc = 2200 см–1, kd = 2800 см–1, ke = = 3400 cм–1, kf = 3800 cм–1, kg = 4400 см–1; на рис. 3: kа* = 1300 см–1, kb* = 1600 см–1, kс* = 2300 см–1, kd* =

= 2900 см^–1, k e* = 3500 cм^–1, k f* = 4200 см^–1, k g* = = 4800 см^–1.

Найдем отношения резонансных волновых чисел. На рис. 2 ( k b / k а ) = (1570 / 1250) = 1.256, на рис. 3 ( k b* / k а* ) = (1600 / 1300) = 1.23. Эти отношения близки к 1.25 = (5 / 4), следовательно, пики поглощения а, а* — четвертые, b, b* — пятые. Значит, k а = k 4 = 1250 см^–1, k b = k 5 = 1570 см^–1, k а* = k 4* = 1300 см^–1, k b* = k 5* = 1600 см^–1. По найденным волновым числам можем найти k 1 = = ( k 4 / 4) = (1250 / 4) = 312.5 см^–1, или k 1 = ( k 5 / 5) = = (1570 / 5) = 314 см^–1 (в среднем k 1 = 313 см^–1) и k 1* = ( k 1* / 4) = (1300 / 4) = 325 см^–1, или k 1* = = ( k 5* / 5) = (1600 / 5) = 320 см^–1 (в среднем k 1* = = 322.5 см^–1). Зная k 1 и k 1* , находим минимальный магнитный момент наночастицы в слабом магнитном поле:

Р 1 = ( h с k 1 / 2 В ) = (6.6·10^–34·3·10⁸·3.13·10⁴ / 2 × × 3·10^–2) = 10.3·10^–20А·м², или

Р 1 = ( h с k 1* / 2 В ) = (6.6·10^–34·3·10⁸·3.22·10⁴ / 2 × × 3.5·10^–2) = 9.1·10^–20А·м².

В среднем Р 1 = 9.7·10^–20 А·м².

Полученное среднее значение минимального магнитного момента Р 1 можно принять за шаг дискретности в магнитном поле с индукцией В ≈ 30 мТл: ∆ Р = 9.7·10^–20 А·м². Это в 1.5 раза больше, чем было получено в более сильном поле. Следовательно, шаг дискретности магнитного момента с уменьшением индукции магнитного поля возрастает. Это позволяет объяснить результаты измерений магнитных моментов наночастиц по кривой намагничивания Ланжевена, согласно которым средний магнитный момент, измеренный в начале кривой (в слабом поле), всегда больше, чем измеренный в конце кривой (в сильном поле) [2, 3]. Подставив ∆ Р в выражение (2), находим длину кванта магнитного потока в поле с индукцией 30 мТл: L f = (∆ P µ 0 / f ) = (9.7·10^–20 ·4 π × × 10^–7 / 2·10^–15) ≈ 0.6·10^–10 м, что в 1.5 раза больше, чем в поле с индукцией 80 мТл, т. е. протяженность кванта магнитного потока возрастает с уменьшением индукции магнитного поля.

Проверим, какие номера n соответствуют пикам а, b, с, d, e, f, g на рис. 2 и 3.

Рис. 2:

пик а — n = ( k а / k 1 ) = (1250 /313) ≈ 4, пик b — n = ( k b / k 1 ) = (1570 / 313) ≈ 5, пик с — n = ( k c / k 1 ) = (2200 / 313) ≈ 7, пик d — n = ( k d / k 1 ) = (2800 / 313) ≈ 9, пик e — n = ( k e / k 1 ) = (3400 / 313) ≈ 11, пик f — n = ( k f / k 1 ) = (3800 / 313) ≈ 12, пик g — n = ( k g / k 1 ) = (4400 / 313) ≈ 14.

Рис. 3:

пик а* — n = ( k а* / k 1* ) = (1300 / 322.5) ≈ 4, пик b* — n = ( k b* / k 1* ) = (1600 / 322.5) ≈ 5, пик с* — n = ( k с* / k 1* ) = (2300 / 322.5) ≈ 7, пик d* — n = ( k d* / k 1* ) = (2900 / 322.5) ≈ 9, пик e* — n = ( k e* / k 1* ) = (3500 / 322.5) ≈ 11, пик f* — n = ( k f* / k 1* ) = (4200 / 322.5) ≈ 13, пик g* — n = ( k g* / k 1* ) = (4800 / 322.5) ≈ 15.

Таким образом, в поле с индукцией 30 мТл дискретность магнитных моментов однодоменных наночастиц тоже наблюдается, но с большим шагом дискретности.

ЗАКЛЮЧЕНИЕ

В ИК-спектрах поглощения магнитных жидкостей, помещенных в магнитное поле, наблюдается несколько дискретных линий с кратными значениями резонансных волновых чисел, что может быть объяснено дискретностью магнитных моментов однодоменных ферромагнитных наночастиц. Дискретность магнитных моментов можно объяснить квантованием магнитного потока внутри наночастиц. Шаг дискретности магнитного момента в магнитном поле с индукцией 80 мТл ∆ Р = = 6.6·10^–20 А·м², а в магнитном поле с индукцией 30 мТл ∆ Р = 9.7·10^–20 А·м², т. е. шаг дискретности магнитного момента возрастает с уменьшением индукции магнитного поля. Это согласуется с тем, что при измерении магнитного момента наночастиц магнитной жидкости по кривой намагничивания Ланжевена в слабом магнитном поле (в начале кривой намагничивания) значение магнитного момента получается больше, чем в сильном магнитном поле (в конце кривой намагничивания) [2, 3]. В предположении, что дискретное увеличение на один шаг магнитного момента однодоменной наночастицы вызвано увеличением на один квант создаваемого ею магнитного потока, определены эффективные протяженности кванта магнитного потока: при В ≈ 80 мТл L f ≈ 0.4·10^–10 м, при В ≈ 30 мТл L f = 0.6·10^–10 м. Таким образом, получается, что эффективная протяженность кванта магнитного потока L f растет с уменьшением индукции внешнего магнитного поля.