Дискретные ортогональные преобразования на фундаментальных областях канонических систем счисления

Первоначальный энтузиазм, вызванный появлением работ, посвящённых фракталам – объектам, которые в классических учебниках математического анализа фигурировали лишь в качестве «патологических» контрпримеров к теоремам («ковёр Серпинско-го», «сапог Шварца» и т.п.), постепенно пошёл на убыль. Между тем самоподобные ветвящиеся струк-туры/объекты на изображениях достаточно типичны и естественны. Эта естественность может объективно определяться как спецификой предметной области, так и субъективным визуальным восприятием или моделью наблюдений.

Именно такие структуры характерны, например, для наномасштабных изображений натурных образцов, для обработки которых приходится использовать традиционный, но всё же паллиативный, математический аппарат цифрового спектрального анализа: дискретные спектральные методы, хорошо зарекомендовавшие себя при обработке и анализе изображений, ориентированы, прежде всего, на применение к изображениям, определённым на прямоугольных областях. Хотя исследователя очень часто интересуют спектральные характеристики объекта, а не «объекта на фоне». В частности, особое место занимают изображения, для которых особенности психофизиологического восприятия человеком порождают оптические иллюзии из-за наличия фона, формирующего в сознании неадекватную интерпретацию изображения. Между тем даже при наличии априорной информации именно о «ветвистом», «самоподобном» характере анализируемого объекта его спектральная специфика может быть учтена только при предварительном «вырезании» этого объекта из малоинформативного (для анализа именно данного объекта) прямоугольного изображения с естественными для такого подхода искажениями спектральных характеристик.

Анонс адекватной для рассматриваемого класса изображений версии спектрального анализа, наследующей в т.ч. и развитую теорию быстрых алгоритмов дискретных ортогональных преобразований, является одной из основных задач работы.

Основную идею предлагаемого подхода проще всего объяснить на примере, указав отличия от традиционных методов и охарактеризовав новые математические идеи, лежащие в основе.

Как известно, дискретное преобразование Фурье (ДПФ) содержит в показателях экспонент билинейную форму, осуществляющую спаривание исходного пространства, на котором определён сигнал, и сопряжённого. Широко известный алгоритм Кули–Тьюки (БПФ) при его реализации осуществляет пространственное или частотное «прореживание» индексов входного или выходного сигнала. В случае преобразования длины, равной степени двойки, эти прореживания могут быть охарактеризованы значением младшего или старшего бита в представлении входных/выходных индексов в обычной двоичной системе счисления. В предлагаемом подходе входные/выходные индексы суть элементы многомерной решётки целых элементов того или иного кольца алгебраических чисел, представленных в т.н. «канонической системе счисления» (КСС) (т.е. системе счисления, основанием которой является не «обычное» целое рациональное, а целое алгебраическое число). При такой интерпретации структурные особенности быстрых алгоритмов сохраняются, но возникают дискретные ортогональные преобразования

Рис. 1. а) Кристалл, б) вирус, в) коралл, г) белковая структура, д) план развития города, е) микродвижения глаза

Рис. 2. Оптические иллюзии

Кроме того, целые квадратичные числа с представлением фиксированной длины в КСС образуют подмножество дискретной решётки со сложной непрямоугольной формой, достаточно часто рассматриваемой в теории фракталов. В частности, для кольца целых Гауссовых чисел и бинарной КСС с основанием a = ( - 1 ± i ) такой областью, т.е. фактически аналогом квадрата, является «дракон Хартера–Хейтуэя» [3] в его предфрактальной версии.

целого в канонической системе счисления. Этот алгоритм сводится к нелинейной, но простой рекуррентной процедуре.

Фундаментальные области, ассоциированные с системами счисления в квадратичных кольцах

Если k = k ( z ) фиксировано, то множество чисел в определении 1, представимых не более, чем k -членной суммой, будем называть k – фундаментальной областью КСС.

Сужение множества «цифр» с I до I ₀ :

10 с Ie{0,.,|Norm(a)|-1} приводит к замене фундаментальных областей КСС на области, аналогичные «ковру Серпинского», а замена «канонического» множества цифр I на множество достаточно произвольных элементов кольца порождает области, примеры которых изображены на рис. 4.

Системы счисления в кольцах целых алгебраических чисел

В 80–е годы появились работы [1], [2], опубликованные в малочитаемых венгерских журналах, в которых дана исчерпывающая классификация так называемых «канонических систем счисления» в кольцах целых квадратичных полей. Эти работы в своё время прошли почти незамеченными. За последующие 30 лет опубликовано более 1000 работ о канонических системах счисления, лишь незначительная часть которых имеет прикладную направленность.

Пусть Q ( sid ) есть квадратичное поле:

Q (V d ) = { z = a + b4d ; a , b e Q } ,

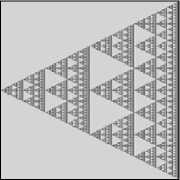
Рис. 3. Фундаментальные области при неполном алфавите

I 0 ^с I

где d – целое число, свободное от

квадратов, S (V d )

– кольцо целых элементов этого поля, то есть множество таких чисел z = a + b4d ; a , b e Q, что их норма Norm ( z ) и след Tr ( z ) есть целые числа:

Рис. 4. Фундаментальные области при полном алфавите I

Дискретные ортогональные преобразования на фундаментальных областях КСС

Norm(z) = (a + b4d)(a -b4d) = a2 -b2d e Z, Tr (z) = (a + bVd) + (a - bVd) = 2a e Z.

Определение 1. Целое алгебраическое число a = A ± dd называется основанием канонической системы счисления в кольце S (V d ) целых элементов поля Q (V d ) , если любой целый элемент этого поля однозначно представим конечной суммой

k ( z )

z = ^ a j a j , a j e I = { 0, . , Norm ( a )| - 1 } . j = 1

Пара {a,I} называется канонической системой счисления в кольце

s (V d )

, а I – алфавитом этой сис- темы. В работах [1] и [2] описан также алгоритм определения цифр в представлении элемента квадратичного

При описании общего подхода синтеза дискретных ортогональных преобразований на k - фундаментальных областях КСС ограничимся иллюстративным примером, в котором основные идеи подхода реализуются в рафинированном виде.

Дискретное преобразование Фурье (ДПФ) длины N = 2 t

N - 1

X ( m ) = ^ x ( n ) exp n = 0

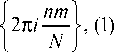
m = 0, ^ , N - 1

запишем в форме

X (m ) = ^x (n) E (m Q n), ne D

m e D = {0,_, N -1},

где операция ⊙ определяет характер «спаривания», т.е. умножения элементов n =( n 0,..., nt-1) и m = (m0,...,mt-1) уже в 2t -мерной алгебре битовых векторов, ассоциированных с представлением чисел

n ^ n = n0 + ...+ nt-1 2 t-1, m ^ m = m0 + ...+ mt-1 2 t-1

в обычной двоичной системе счисления.

Специфика функций E(n) = exp(2ninl для ДПФ [ N полностью определяется следующими условиями:

E ( 0 ) = 1;

E (p + q ) = E (p) E (q),

а также теми значениями, которые E (n) принимает на векторах ек = (80, k ’• ••’ 8 t-1, к ) , где 8i,j - дельта функции Кронекера.

Заметим, что для ДПФ справедливы равенства

E ( ё . ) = 1 , E ( ё . - 1 ) = - 1 и E ( 2 ё . ) = ( E ( ё . ) ) 2 .     (3)

Последнее соотношение индуцирует равенство

л(ек+1 ) = Л2 (eк )л(ек-1), дляS(i)

* ^л(^е к + 1 ) = ^{л 2} (^е к ) ,         дляS ( i42 )

^л(^е к + 1 ) = ^л(^е к ) ^{л 2} (^е к - 1 ) , для S ( i 41 )

с основаниями а1 = -1 + i, а2 = i 42, а7

- 1 + i 41

соответственно.

Теорема 1. Преобразование (5) с базисными функциями, определёнными соотношением

(      2 к+1 I exp 2п i---=

I N

Г exp

I

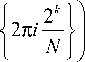
которое уже пере-

стаёт быть верным, если векторы n и m ассоцииро-

является ортогональным, т.е.

^Л (n) Л * (к ) = 2t 8„,к, nG Dt

ваны с элементами квадратичного кольца

S ( 4d ) ,

элементы которого представлены в бинарной системе счисления с основанием а ^ 2 .

Как известно [1], [2], существуют ровно три квадратичных кольца, в которых есть бинарные системы счис-

ления, а именно:

S ( i ) , S ( i 41 ) , S ( i 41 ) . Основания

бинарных КСС квадратичных колец S ( i ) ,

S ( i 41 ) ,

S ( i 41 )

удовлетворяют квадратным уравнениям:

а 2 + 2 а 1 + 2 = 0,

а 2 + 2 = 0,

а 7 + а ₇ + 2 = 0.

Поэтому будем искать комплекснозначные базисные функции преобразования

X ( w ) = ^ x ( z ) Л ( z О w ) , w ^G D t ,            (5)

Z G D_t

где * - знак комплексного сопряжения.

Быстрые алгоритмы

Ограничимся для наглядности иллюстрацией функций Л ( n О m ) , определённых на простейшей области («дракон Хартера–Хейтуэя»), являющейся фундаментальной областью для кольца целых Гауссовых чисел S ( i ) . Нетрудно заметить, что условия (1)–(3) определяют характер аддитивной циклической группы G = C N , N = 2 t , а условие (4) определяет специфику спаривания ассоциированного с этой группой 2 ^t -мерного «битового» пространства с сопряжением к нему. При выборе другой интерпретации ассоциированного пространства и другого принципа спаривания получится и другое преобразование, отличное от описанного выше «фурьеподобного» ДОП.

где D_t – t-фундаментальная область КСС для

S ( i4d ) ,

удовлетворяющие условиям:

Рис. 5. Вещественные части базисных функций «фурьеподобных» преобразований

Например, при определении операции ⊙ как побитового умножения векторов n и m получается «хаароподобное» ДОП, изображения базисных функ-

Л ( 0 ) = 1 = Л ( e t ) ,

^Л ( p ⁺ q ) = ^л ( p ) ^л ( q ) , ^л ( ^e t + 1 ) = ^{- 1} ,

exp < -паtак + паtак ]    д„„С(а 21            |, ля (^) Л (е к ) = exp ^ -паа +паа 1 , для S i 2 2 * 22( ) ^exp j -паtак + паtак 1 , для S i 7 2 t-1471 ’ ций которого приведены ниже. Его базисные функции являются характерами группы G ≅ C2 ⊕…⊕ C2 . При аналогичном рассмотрении группы

G≅C ⊕…⊕C 2α1 2αs получаются ДОП-аналоги преобразований Виленки-на–Крестенсона и т.д. Заметим, что в силу метода построения базисных функций для рассмотренных преобразований наследуются все общие принципы синтеза быстрых алгоритмов ДОП [4].

Рис. 6. Базисные функции «хаароподобных» преобразований

Рис. 7. Базисные функции аналогов преобразования Виленкина–Крестенсона

Заключение

Нетрудно заметить, что Теорема 1 легко обобщается на случай произвольной КСС, с ограничениями на «канонический» алфавит I , соответствующими связи параметров d и α , определёнными утверждениями работ [1], [2]. Также несложным является обобщение Теоремы 1 на случай «неполного» алфавита I 0 ⊂ I .

По-настоящему сложной и интересной задачей является синтез ДОП на фундаментальных областях для алфавитов достаточно произвольной природы, что является предметом специального перспективного исследования.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках постановления Правительства Российской Федерации от 9.04.2010 г. № 218: договор № 02.Г36.31.0001 от 12.2.2013 и Российского фонда фундаментальных исследований (гранты    12-01-00822-а,    13-01-97007- р_поволжье_а, 12-01-31316 мол_а).