Дискретные преобразователи перемещения с кинестетическими датчиками положения

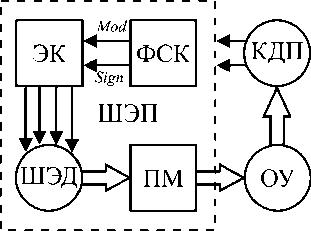
Введение контура главной обратной связи (ГОС) по перемещению устраняет основной недостаток разомкнутого ШЭП. В робототехнике и мехатронике наибольшее распространение получили кинестетические датчики перемещения (КДП). В настоящее время свыше 70 % информационных устройств промышленного производства реализуют кинестетические функции [2].

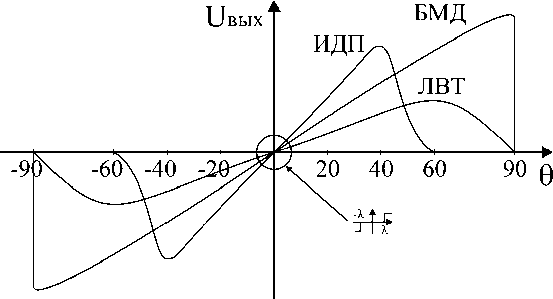
На рис. 1, б представлены выходные характеристики трех типов КДП: индукционного датчика положения (ИДП), линейного вращающегося трансформатора (ЛВТ) и бесконтактного магнитного датчика (БМД). Для линейного преобразования перемещения в диапазоне ±360º используются преобразователи «угол – параметр-код» с синуснокосинусным вращающимся трансформатором (СКВТ) [2] в амплитудном или фазовом режимах [3]. Механически КДП сопрягается непосредственно или через передаточный механизм (ПМ) с ОУ, а информационно – с ФСК (см. рис. 1, а).

Вариант ЭМП (рис. 2, а) с транзисторным электронным коммутатором (ЭК) и ШЭД типа ДШ-0,04В потребляет от сети до 30 Вт при парной коммутации в режиме фиксированной стоянки под

а)

б)

а)

Рис. 2. Вариант ЭМП с транзисторным ЭК (а) и ШЭД типа ДШ-0,04В (б)

Рис. 1. Структура ЭМП с ШЭД (а) и выходные характеристики КДП (б)

б)

током. Электроника размещается на типовой плате. Механизм (рис. 2, б) состоит из цилиндрической и червячной передач – последняя является необратимой, что устраняет влияние ОУ через ПМ на ШЭД.

Электромехатронный преобразователь (ЭМТП) благодаря структурным и алгоритмическим изменениям в электронной части позволяет в 2 раза повысить энергоэффективность преобразования за счет использования ШЭД большей мощности с прежним потреблением от сети и механизмом (см. рис. 2, б).

ЭМТП отличается от ЭМП следующими особенностями.

• 1.    Синергическим характером интеграции составляющих, который определяется тем, что создается устройство, обладающее свойствами, превышающими возможности каждого из них и их суммы.

• 2.    Непременным условием создания ЭМТП является его интеллектуализация на основе оценки значений координат перемещения, за которые приняты позиционная ошибка или скорость ее изменения.

Поскольку ЭМТП должен обладать интеллектом, то наличие ГОС является не только достаточным, но и необходимым условием отнесения этого преобразователя энергии и формы информации к ЭМТП. Наличие контура ГОС позволяет придать ему второй необходимый и достаточный признак – синергетический эффект, позволяющий в результате интеграции в едином устройстве информационной и исполнительной частей получить эффект, превышающий сумму эффектов составляющих.

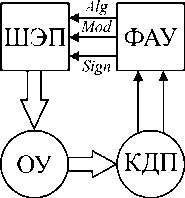
Повышение эффективности замкнутых ЭМТП с ШЭД стало возможным благодаря использованию их алгоритмических возможностей в части микропрограммного управления [3]. Это позволило реализовать самоорганизующиеся структуры интеллектуальных ЭМТП, обладающих синергией на основе структуры, представленной на рис. 3, а.

В отличие от структуры ЭМП (см. рис. 1, а) она содержит формирователь алгоритмов управления (ФАУ), который действует на основе оценки информации, поступающей от КДП, формируя сигнал Alg смены алгоритма управления ШЭД. В пределах линейной части выходной характеристики КДП (см. рис. 1, б) ШЭД управляется по алгоритму парной коммутации в направлении умень-

а)

б)

Рис. 3. Структура ЭМТП (а) и его микроэлектроника с ШЭД типа ДШ-0,1В (б)

шения рассогласования. При входе в зону нечувствительности ±λ (см. рис. 1, б) ротор ШЭД фиксируется на алгоритме поочередной коммутации, при котором потребление тока снижается вдвое по сравнению с алгоритмом парной коммутации. С целью устранения периодических режимов направление последнего шага сохраняется прежним относительно направления входа в зону, что приводит к снижению погрешности позиционирования и износа элементов ПМ. Построение и работа ФАУ описаны в [3].

Структурное, алгоритмическое и информационное обеспечение процесса управления в сочетании с удачной конструкцией ПМ (см. рис. 2, б) позволили реализовать в процессе модернизации самоорганизующийся ЭМТП с удвоенным выходным моментом за счет применения ШЭД типа ДШ-0,1В (рис. 3, б) без увеличения потребляемой мощности. Микроэлектроника ЭМТП выполнена на отечественных ИМС и размещена на типовой плате (рис. 3,б). В настоящее время ведутся работы по замене ИМС средней степени интеграции на микроконтроллер типа AVR.

Изменение структуры может иметь одну из трех целей: расширение адаптивных и функциональных возможностей, совершенствование систем в процессе эксплуатации. Рассмотренный пример самоорганизующейся ЭМТП с ШЭД иллюстрирует одновременную реализацию всех трех целей, т. е. комплексное решение задачи повышения эффективности.

При решении задачи идентификации динамических свойств комплекса «ЭК-ШЭД», являющегося основным динамическим звеном замкнутого ЭМТП, был учтен постулат академика А.Ю. Ишлинского о том, что САУ любой сложности реагирует на входное ступенчатое воздействие, в нашем случае переключение обмоток ШЭД, подобно звену второго или третьего порядка. Эксперимент и моделирование подтвердили правомерность применения постулата [4].

Анализ устойчивости замкнутого ЭМТП с ШЭД произведен в соответствии со структурой на рис. 4. Пользуясь теоремами смещения, линейно-

сти и сдвига, получим импульсную передаточную функцию для импульсной системы с безразмерным временным запаздыванием σ = t_З/T_У [5]:

K ( q , ^{е )} =

e q     e ^{2 q} cos гое- e ^q e^ cos го (1 -e ) _ _ЛЕ

^     e ^q sin го (1 -ст ) + e ^л sin гост - _л ( _{1 -ст} )

1 -^2 e2 q -2eqe"л cos ГО + e"^ 6

^^^^^™

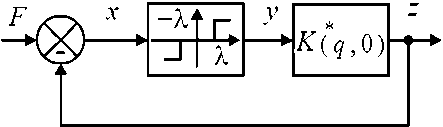
Рис. 4. Эквивалентная структура ЭМТП с ШЭД

Оптимизация величины редукции ПМ.

Диапазон вариаций редукции i р ПМ ограничен условиями, в которых для достижения требуемого

быстродействия

i_РБ = α_дв ·f _упр / Ω_max,

а для получения необходимой точности

ⁱРБ ^ ^ дв / ^ доп ,

где «„„ - величина шага двигателя; f,, - частота дв                                       упр

управляющих импульсов; Q max - максимальная скорость входного воздействия; 8 _доп - допустимая величина статической ошибки ЭМТП.

Определим выражение для получения оптимального передаточного числа ПМ, обеспечивающего максимальные ускорения исполнительного вала механизма. Из выражений (2) и (3) легко получить пределы изменения нагрузочного момента двигателя; линеаризуя зависимости в предлагаемых рабочих точках характеристики, получаем выражение вида

(  j3

f дв = f 0 1 - к^

V      ^J р J

^^^^^^в

^k 1 ^M пр ,

где f ₀ – частота импульсов холостого хода ШЭД; k – коэффициент, учитывающий влияние момента инерции нагрузки; k ₁ – коэффициент, учитывающий влияние момента нагрузки типа «сухого» трения; М пр – приведенный к валу ШЭД момент нагрузки.

Скорость ω Н выходного вала ПМ определяется выражением

связано с импульсным возбуждением обмоток двигателя и приводит к дискретному характеру перемещения ротора. Это дискретное перемещение, сопровождающееся колебаниями ротора в пределах шага (1), вызывает существенное увеличение динамических нагрузок на ПМ. Поэтому

вопросы, связанные с исследованием механизмов с ШЭД, имеют важное точки зрения эксплуатации.

Идентификация динамических

надежности значение с

показателей

а

® н = -дв Я0 i р

1-

JH   т

н

. 2 т ^ред

V i р

р

Приравняв нулю производную

выражение

2 k 1 M н

р

^^^^^^в

^k 1 ^{M н} i _р

^ . (5)

d юн н , получим diр

1 - к ^

J

-j- = 0.

1 - к^ рд

J _р

Оптимальное передаточное число i опт ПМ ределяется:

оп-

iопт

k 1 M н

+

k 1 M н

+

1 - к ^еД J р J

1 - к ^реД J р J

3 k ^{J н} J _р

1 - J

J _р

.

Величина момента инерции ПМ, как показывает опыт проектирования ЭМТП с ШЭД, находится в диапазоне

J ред = (0,3...0,8) J р .

Наряду с положительными сторонами при ис-

пользовании ШЭД в просы, связанные с

ЭМТП часто возникают во-проектированием ПМ. Это

а)

ЭМТП с ШЭД [4] позволяет по иному подойти к исследованию надежности механических передач. В связи с тем, что при больших изменениях физических параметров ЭМТП с ШЭД его относительные единицы [1] изменяются в сравнительно небольших диапазонах, удается обойтись сравнительно небольшим числом испытаний и результаты этих испытаний распространить на большое число ПМ.

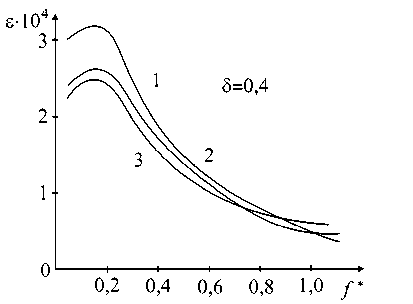
Для определения динамических нагрузок, действующих на механизмы, необходимо определить величину угловых ускорений. Используя систему относительных единиц и эквивалентную структуру ЭМТП с ШЭД (см. рис. 4), удается построить зависимость относительного ускорения ε как функцию относительной частоты управляющих импульсов f ^* (рис. 5, а). Определение относительного ускорения проводилось методом фазовой поверхности (характеристика 1), при моделировании на ЭВМ (характеристика 2) и экспериментально (характеристика 3). Величина истинного ускорения легко определяется из соотношения

d 2 0 m 0 d 2 6 M max d 2 6 —— =---=---— .

dt ²    p  d т J ₂    d г²

Сопоставляя результаты (рис. 5, а), можно отметить, что в расчетах надежности при определении ускорений, действующих на ПМ, можно использовать метод фазовой поверхности, который дает несколько завышенные результаты. Экспериментальные характеристики износа приведены на рис. 5, б.

Результаты испытаний показали недопустимость возникновения в ЭМТП с ШЭД периодиче-

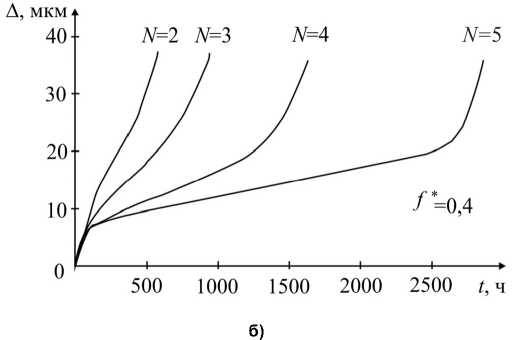
Рис. 5. Характеристика износа

ских режимов с малыми периодами даже несмотря на то, что они могут не влиять на качество всей системы. Если при отсутствии периодических режимов продолжительность наработки t до катастрофического износа составляет приблизительно 2500 часов, то при наличии периодических режимов износ до того же уровня наступает значительно быстрее. Так, например, если периодический режим имеет относительный полупериод N =2, то продолжительность наработки составляет всего 250 часов (рис. 5, б).

Введение контура местной обратной связи (МОС) переводит БЭПМ в режим вентильного электродвигателя (ВЭД), имеющего по сравнению с ШЭД более высокую энергоэффективность. Благодаря количественным изменениям динамические характеристики ЭМТП претерпевают качественное изменение, состоящее в переходе от колебательного характера перемещения в пределах шага к апериодическому, что согласуется с положениями упомянутого выше постулата.

Переход в ЭМТП на использование ВЭД вместо ШЭД позволяет удвоить ресурс работы элементов ПМ до катастрофического износа. Дальнейшее повышение надёжности ЭМТП достигается в его безредукторных вариантах [5, 6].

В заключение следует отметить, что исполнение ПМ характеризуется большим разнообразием, так же как и существенными вариациями нагрузок, действующими на механические передачи. Поэтому создание прецизионных ЭМТП [7], обладающих повышенной мощностью является перспективным направлением электромеха-троники.