Дисперсия обратных объёмных магнитостатических волн в средах с поглощением

Введение. Несмотря на то, что магнитостатика является лишь приближением общей электродинамики, в её рамках возможно описать работу множества устройств спинволновой электроники [1-3]. Спиновые волны – это волны намагниченности в магнитоупорядоченных веществах.

Одним из направлений спинтроники является разработка устройств на объёмных магнитостатических волнах (ОМСВ). На основе ОМСВ создаются компактные СВЧ-устройства аналоговой и цифровой обработки информации. Вместе с тем, подавляющее большинство исследований ОМСВ выполнено без учета затухания [1-4]. Исследование влияния поглощения волн в веществе позволит усовершенствовать работу устройств на ОМСВ.

Основные уравнения и геометрия задачи. Геометрия задачи представлена на рис. 1. В работе рассматривается случай касательно намагниченной до насыщения безграничной ферритовой плёнки толщиной d . Плоскость yOz соответствует плоскости пленки, положения границ определяются координатами x=±d/2 . Пленка намагничена до насыщения постоянным полем H , приложенным вдоль оси Oz . Угол между волновым вектором и осью Oy обозначен как φ .

В магнитостатическом приближении магнитные уравнения Максвелла имеют вид [5, 6]:

rotH = 0

div (H + 4 pM ) = 0

Вводя магнитостатический потенциал ψ согласно

H = grady/                     (2)

с помощью (1) получаем уравнение Уокера

AY + 4 TrdivM = 0                 (3)

Уравнение Ландау-Лифшица с диссипативным членом в форме Гильберта имеет вид:

⁸ M

--= - y [ M x H ]+— dt      L J M 0

⁸ M

M x-- d t

здесь М ₀ – постоянная длина вектора намагниченности, γ – гиромагнитное отношение, α – параметр диссипации.

Дисперсионное соотношение, полученное с помощью совместного решения уравнений (1), (3), (4) имеет вид:

tg ( kd S) = 2^-

- 1

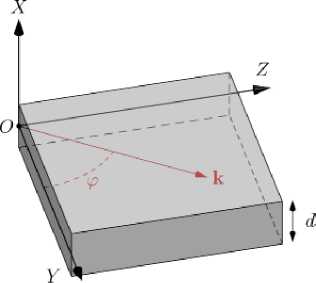
Рис. 1 – Геометрия задачи

sin2

S = cos ф+--—

V И P = v2 cos ф - 2P2P где θ, β – вспомогательные параметры, зависящие от приведённой частоты волны Ω; μ – магнитная проницаемость, ν – компонента побочной диагонали тензора магнитной восприимчивости.

В нашем случае параметры ν, μ, β, θ , также как и волновой вектор k=η-iξ – комплексные. Мнимая часть ξ волнового вектора определяет логарифмический декремент затухания.

Левая часть соотношения (5) – есть функция одновременно волнового вектора k и частоты Ω. Однако, с помощью вспомо-

гательных обозначений (6), легко можно разделить переменные.

Z = arctg

3M1

I - 1 J

При этом дисперсионное соотношение (5) запишется так:

77 d = ^

5d =

s' z 43" z "  s ' ²+У"² 3' z '-3" z "  s '2 + 3"^г

В произвольной геометрии дисперсия ОМСВ с учетом затухания имеет достаточно сложный характер. На рис. 2 представлены дисперсионные кривые первых пяти мод объёмных магнитостатических волн для действительной части волнового числа в случае угла φ=π/2 , без учёта затухания ( α =0). Анализ дисперсионных кривых показывает, что в нашем случае могут распространяться только обратные объёмные МСВ (ООМСВ).

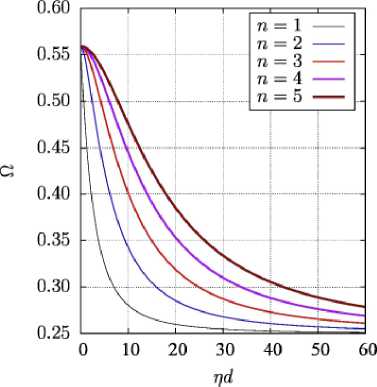
Рис. 2 – Дисперсия ООМСВ. Первые пять мод без затухания α=0. Угол φ=π/2

На рис. 3 изображена зависимость частоты первой моды ООМСВ от действительной части волнового числа при разных углах без учёта затухания. Можно заметить, что с увеличением угла отклонения φ волнового вектора от направления магнитного поля частотный спектр ООМСВ расширяется.

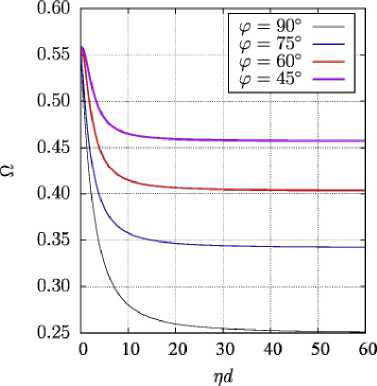
Рис. 4 иллюстрирует влияние затухания на дисперсионные характеристики первых четырёх мод ООМСВ, которое прояв-

Рис. 3 – Дисперсия ООМСВ первой моды без учёта затухания α=0 при разных углах φ ляется в том, что волновое число ограничивается как сверху (в области низких частот), так и снизу (в области высоких частот). Из рисунка также следует, что учёт затухания кроме ограничения возможных значений волнового числа (а значит, и длины волны ООМСВ) влияет на форму дисперсионных кривых. Это означает, что наличие затухания изменяет скорости распространения волн.

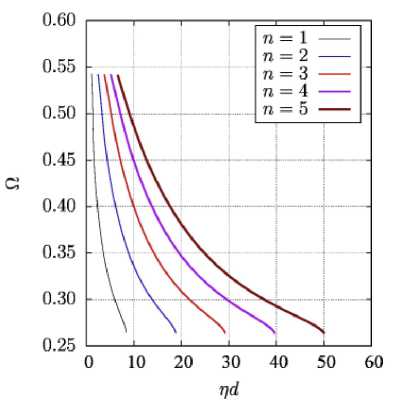
Рис. 3 – Дисперсия ООМСВ первых пяти мод с учётом затухания α=0.05. Угол φ=π/2

Таким образом, в данной работе были получены дисперсионные соотношения для ООМСВ с учётом затухания. Обнаружено, что диссипация приводит к ограничению спектра ООМСВ не только по частоте, но и по длине волны.