Дисперсия оптических волноводных мод тонких лево-ориентированных пленок

Возможность использования лево-ориентированных материалов ( left-handed materials , LHM) с одновременно отрицательными значениями диэлектрической и магнитной проницаемостей в планарных оптических волноводах разнообразила их пространственные структуры. Существует несколько возможных вариантов таких структур: пленка из LHM – покровная среда и подложка на основе обычных право-ориентированных материалов ( right-handed materials , RHM); пленка и подложка из LHM – покровная среда из RHM; все слои из LHM. С точки зрения структур, которые уже созданы и исследуются экспериментально, наибольшее значение имеют пленки из LHM с прилегающими слоями из RHM [1, 2]. Ниже будет рассмотрена частотная дисперсия волноводных мод таких структур.

2.    ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Литвинов Рудольф Викторович, кандидат физико-математических наук, доцент кафедры телекоммуникаций и основ радиотехники.

Полагая, что векторы электрической и магнитной напряженностей светового поля удовлетворяют уравнениям Максвелла и, используя граничные условия, можно получить дисперсионное уравнение относительно постоянных распространения β волноводных мод ТЕ -типа в виде [2]:

tanh χ _f h

χ _s µ _f χ^- _f ¹ µ^- _s ¹ + χ _c µ _f χ^- _f ¹ µ _c ^{- 1} 1 + χ _s χ _c µ ² _f χ^- _f ² µ _s ^{- 1} µ _c ^{- 1}

где µc, µf и µs – относительные магнитные проницаемости покровной среды, пленки и под ложки, соответственно;

χ∗= β2-ε∗µ∗(ωυñ)2 , (2)

коэффициенты, зависящие от величины постоянных β (в нижнем индексе вместо букв « с , f или s » используется знак «*» для сокращения записей), определяют характер пространственного распределения светового поля в покровной среде « c », подложке « s » и пленке « f »; ε _*– относительная диэлектрическая проницаемость материалов слоев волновода. Если в формуле (1) выполнить замену « µ_∗↔ε_∗ », то получившееся новое соотношение будет дисперсионным для мод TM -типа.

Пространственная неограниченность покровной среды и подложки в направлении перпендикулярном пленке, в которой должно быть локализовано поле моды волновода, приводит к требованию вещественности коэффициентов χ _c и χ _s . Центральная пленка является ограниченной в поперечном направлении и, поэтому в общем случае, коэффициент χ _f может принимать как мнимые, так и вещественные значения [2, 7].

Величина вещественных постоянных распространения β планарных волноводов, изготовленных из обычных RHM с одновременно положительными значениями проницаемостей (εc,s>0 и µc,s>0), ограничена условием max [ nc; ns ] го/c < в < n^. го/c, где nc, s = ^ £ c, s ц c, sго cc - показатель преломления материалов слоев волновода [3, 4, 7]. В этом случае, коэффициент χf принимает мнимые значения. Фазовая скорость волноводных мод такого волновода (быстрых мод) больше фазовой скорости плоских электромагнитных волн в объемных средах из материалов покровной среды и подложки.

Если центральная пленка волновода выполнена из LHM, то коэффициент χ _f может принимать и вещественные значения. В этом случае, в волноводе могут распространяться не только быстрые, но и медленные моды, фазовая скорость которых меньше фазовой скорости плоских электромагнитных волн в объемных средах с материальными параметрами, соответствующими параметрам слоев волновода.

Следуя работам [5, 6], будем считать, что зависимость диэлектрической £ f и магнитной ц f проницаемости объемной среды из LHM от частоты го электромагнитного поля описывается соотношениями

_ i 2/2 i i- 2 / 2 2 \ 1

£ f = 1 — to p to , Ц f = 1 — F ГО ( ГО — ГО о ) , (3) где го p - плазменная частота, го ₀ - частота магнитного резонанса, F – фактор заполнения метаматериала ( 0 <  F <  1 ).

Из анализа соотношений (3) следует, что в случае выполнения условия го₀< го _p < ro₀/V 1 — F интервал частот го , в котором диэлектрическая и магнитная проницаемости таких сред являются одновременно отрицательными, лежит в пределах го ₀ < го < го _p . В случае го _p > го₀ /V1 — F , этот интервал имеет пределы от го ₀ до го ₀ /V1 — F и определяется только областью отрицательных значений магнитной проницаемости. Дисперсия материальных параметров обычного право-ориентированного материала в указанных интервалах длин волн в оптическом диапазоне пренебрежимо мала в сравнении с дисперсией лево-ориентированного и ниже не учитывается.

• 3.    ДИСПЕРСИОННЫЕ ЗАВИСИМОСТИ ЭФФЕКТИВНЫХ ПОКАЗАТЕЛЕЙ

ПРЕЛОМЛЕНИЯ

Выполним анализ зависимостей эффективных показателей преломления neff, = ви /го от длины световой волны X оптических мод тонкой пленки из LHM с воздушной покровной средой (£c = 1 и цc = 1) для трех случаев немагнитных подложек (цs = 1) с различными величинами диэлектрической проницаемости £s, равными 1; 1,5; и 2. Будем считать, что дисперсионные зависимости материала тонкой пленки определяются параметрами гоp = 3,46 -1015 рад/с, го0 = 1,63 -1015 рад/с и F=0,5, согласующимися с данными работы [8]. В этом случае, диапазон X, в котором одновременно выполняются условия £ f < 0 и цf < 0 , лежит в пределах от 0,816 мкм до 1,155 мкм.

Результаты численных расчетов зависимостей n eff ( X ) для ТЕ -мод представлены на рис. 1 а и 1 б сплошными кривыми для случаев толщины пленки 100 нм и 330 нм, соответственно. Здесь же представлены дисперсионные зависимости показателя преломления объемного лево-ориентированного материала n f = ^£ f ц f (штрихованные кривые) и уровни (пунктирные) показателей преломления подложки n s = ^£ s ц s .

Общей особенностью полученных дисперсионных зависимостей для ТЕ -мод является то, что они лежат не только в области быстрых мод

(ns < neff < nf), что характерно для обычных пленок из RHM, но и в области медленных мод (neff > max (nf,ns)), которая у RHM-пленок отсутствует [3, 4]. Независимо от толщины LHM-пленки ее дисперсионные зависимости обладают двумя сингулярными точками. Причиной появления первой из них является резонанс магнитной проницаемости цf (го) объемного материала при частоте го0 (см. (3)). Вторая сингулярность находится в точке X = 1 мкм, где магнитная проницаемость принимает значение цf = — 1. В окрестности этой точки дисперсионные кривые медленных мод волновода асимптотически приближаются к дисперсионным кривым поверхностных электромагнитных волн s-типа [9, 10], фазовые скорости которых обращаются в ноль при равенстве цs = цf = цc = 1, выполняющегося для принятых условий как раз при длине волны 1 мкм.

Дисперсионные зависимости мод TE ₀₀ LHM-пленки толщиной h =100 нм лежат в медленной области и обладают точкой с нулевой групповой скоростью и g = d го/ d р = 0 , в которой dn effj d X = ^ (см. рис. 1 а ). Эта точка делит дисперсионную кривую на две ветви. Нижняя ветвь соответствует положительной групповой скорости ( и g >  0 , фазовая и групповая скорости

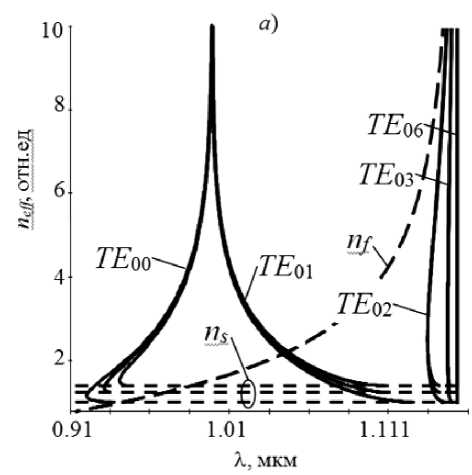
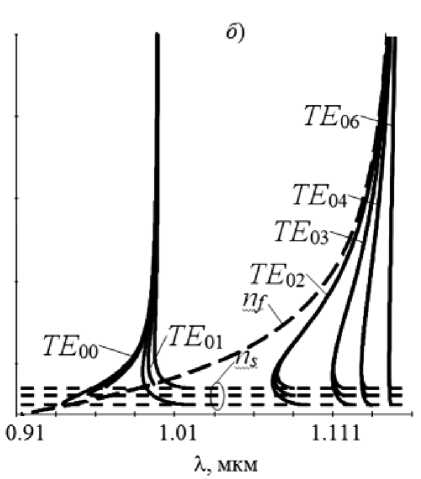
Рис. 1. Зависимости n eff ( X ) ТЕ -мод пленки толщиной 100 нм (а) и 330 нм (б).

имеют одинаковое направление), а верхняя – отрицательной ( и g < 0 ,фазовая и групповая скорости имеют противоположные направления). Дисперсионные зависимости TE ₀₁ моды лежат как в области медленных, так и в области быстрых мод, им соответствует положительная величина и g >  0 . Дисперсионные зависимости остальных мод лежат в быстрой области. Однако в отличие от обычных пленочных волноводов из RHM, дисперсионные зависимости мод которых являются монотонными, дисперсионные зависимости быстрых мод волноводов с LHM-пленкой делятся на две ветви точкой, соответствующей случаю и g = 0 (аналогично зависимостям TE ₀₀). При этом с ростом номера моды LHM-пленки ее дисперсионные зависимости, приближаясь к области сингулярности проницаемости ц f , практически сливаются.

Дисперсионные зависимости n eff ( X ) для ТЕ -мод, соответствующие более толстой LHM-пленке c h =330 нм (см. рис. 1 б ), также лежат в области медленных и быстрых мод. Однако в этом случае, в отличие от случая h =100 нм, дисперсионные зависимости для TE ₀₁ моды являются немонотонными, делятся точкой с и g = 0 на верхнюю и нижнюю ветви, отвечающие различным направлениям групповой скорости. Таким образом, увеличение толщины пленки может изменить направление групповой скорости ТЕ -моды с совпадающего с направлением фазовой скорости на противоположное ей.

Характерно, что изменение показателя преломления подложки (асимметрия пленочного

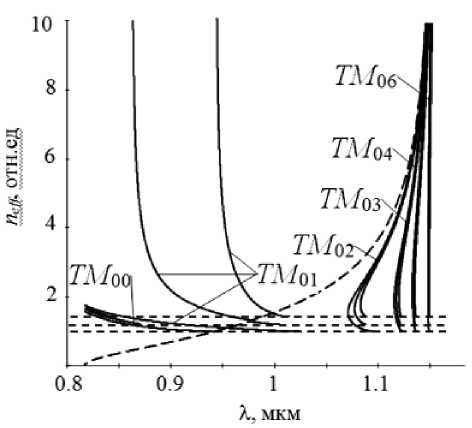
Рис. 2. Зависимости neff (X) ТМ-мод пленки толщиной 330 нм волновода) заметно сказывается на дисперсионных зависимостях только в области отсечки

ТЕ-мод (neff « ns ). При этом в LHM-волноводе с h=100 нм (см. рис. 1а) это изменение не приводит к качественному изменению характера дисперсионных зависимостей neff (X), практически влияя только на условия отсечки. В более толстом волноводе с h=330 нм (см. рис. 1б) увеличение показателя преломления подложки может привести к отсечке ветви дисперсионной кривой, лежащей ниже точки с нулевой групповой скоростью. Поэтому в более толстом ассиметричном (ns=2) пленочном волноводе дисперсионная зависимость neff (X) моды TE00 является монотонной, соответствует одинаковым направлениям фазовой и групповой скорости.

Результаты численных расчетов зависимостей n eff ( X ) для TM -мод пленки толщиной 330 нм представлены на рисунке 2. Качественный характер зависимостей, лежащих полностью в области быстрых мод (моды ТМ ₀₂, ТМ ₀₃ и т.д.) такой же, как и у аналогичных зависимостей ТЕ -мод. Однако характер дисперсионных зависимостей мод ТМ ₀₀ и ТМ ₀₁, лежащих в областях быстрых и медленных мод, сильно отличается от зависимостей мод ТE ₀₀ и ТE ₀₁. Положение сингулярности на зависимости n eff ( X ) ТМ 01 , расположенной в области медленных мод, зависит от величины диэлектрической проницаемости подложки s _s . В этой области дисперсионные зависимости этой моды асимптотически приближаются к дисперсионным кривым поверхностных электромагнитных волн p -типа [9, 10] на границе пленка-подложка, фазовые скорости которых обращаются в ноль 22

при выполнении равенства s ₅ = s f . В рассматриваемом случае, это условие выполняется для двух значений s _s = 1 и 2. Отметим, что условие 222

s ₅ = s f = s c = 1 выполняется за пределами рассматриваемого диапазона длин волн, поэтому сингулярность, на отвечающей этому случаю кривых n eff ( X ) для мод ТМ _0О и ТМ 01 , отсутствует.

Еще одним качественным отличием направляемых свойств LHM-пленки от аналогичных свойств RHM-пленки является существование трех диапазонов длин волн, в которых существует только одна из мод типа ТЕ ( ТЕ ₀₀,₀₁,₀₂) или одна из мод типа ТМ ( ТМ ₀₀,₀₁,₀₂). В то время как для обычных пленочных волноводов из RHM одномодовый режим реализуется только для фундаментальной моды ( ТЕ ₀₀ или ТМ ₀₀) [3, 4, 7].

4.    ЗАКЛЮЧЕНИЕ

Таким образом, дисперсионные свойства оптических мод планарного волновода с пленкой на основе LHM качественно отличаются от дисперсионных свойств обычных волноводов на основе RHM. Моды двух первых порядков, в зависимости от длины волны, могут быть как быстрыми, так и медленными. В общем случае, групповая скорость моды может совпадать с фазовой, быть противоположной ей или обращаться в ноль. Одномодовый режим может быть реализован для трех мод низшего порядка.

Работа выполнена по заданию Минобрнауки РФ (проект № 2406). Шибельгут А.А. поддержан стипендией Президента РФ (проект СП-4673.2013.5).