Дисперсия продольных волн, распространяющихся в материалах с точечными дефектами

ВЕСТНИК ПНИПУ. МЕХАНИКА № 5, 2023PNRPU MECHANICS BULLETIN

С 80-х гг. прошлого века интенсивно изучается влияние лазерного излучения на материалы. Теоретически и экспериментально было показано, что под воздействием лазерного луча в материалах образуются многочисленные точечные дефекты (вакансии, межузельные атомы), создающие в поверхностном слое напряженно-деформированное состояние [1–9].

Генерация точечных дефектов в материалах наблюдается и при ионной имплантации [10–24].

Прохождение продольной акустической волны способствует изменению в областях растяжения и сжатия энергии активации образования точечных дефектов, приводя к их пространственному перераспределению. Дефекты, мигрирующие по материалу, рекомбинируют на различного рода центрах. Роль таких центров могут играть дислокации, примеси внедрения и др.

Волновые эффекты в ансамблях дислокаций изучались в работах [25–29].

В [6] показано, что задачу о распространении акустической волны в материале с точечными дефектами следует рассматривать как самосогласованную, включающую в себя, наряду с динамическим уравнением теории упругости, кинетическое уравнение для плотности дефектов.

В [30] исследовано взаимодействие нелинейной волны деформации с полем концентрации точечных дефектов (вакансий, межузлий), приводящее как к рассеянию волны, так и к изменению энергии активации образования дефектов и их пространственному перераспределению. При этом предполагалось, что основными процессами, определяющими поведение дефектов, являются процессы генерации, рекомбинации и диффузии. Объемная взаимная рекомбинация разноименных дефектов не учитывалась.

В [31; 32] совместно с полем концентрации одного типа точечных дефектов проанализировано влияние внешнего нестационарного неоднородного температурного поля на нелинейные волны деформации.

В настоящей работе в линейной постановке задачи изучается дисперсия продольных волн, распространяющихся в материалах с точечными дефектами при учете объемной взаимной рекомбинации разноименных дефектов.

1. Постановка задачи

Распространение гармонической волны описывается линейной системой [6]:

d ² U _ 2 <'U d t ² l d x ²

_

X +— ц

Q V p

d « v d x

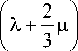
Q. i d n i p d x

д n_y     д U     д ² n_y

-^ = q _E^ + D v —v -P v n v д t      д x        д x

P iV n i ,

д n, _ д U _ д² n i

= q_;      + D       в, n — в nv .

д t ^E д x       ¹ д x ^{2        1} V

где to и k - частота и волновое число волны. Составляем определитель системы и приравниваем его нулю.

Дисперсионное уравнение в безразмерных переменных

Здесь U ( x , t ) - продольное перемещение частиц материала (волна считается плоской); n j ( x , t ) - объемная концентрация точечных дефектов ( j = V - для вакансий, j = i - для межузлий); c l = ( X + 2 ц)/р - скорость, с которой распространялась бы продольная волна в материале, если бы в нем отсутствовали дефекты; X , ц - константы Ламе; р - плотность материала; Q j -дилатационный параметр, характеризующий изменение объема материала при образовании в нем одного точечного дефекта. Для вакансий Q j <  0, для межузлий Q j >  0. Через q ₀ обозначен темп генерации точечных дефектов в отсутствие деформации; второе слагаемое в правой части (2) представляет собой деформационную поправку в генерацию дефектов; D_j – коэффициент диффузии дефекта типа j ; в j - скорость рекомбинации на стоках. Через в _iV и в _Vi обозначены скорости взаимной рекомбинации дефектов типа «межузлие– вакансия» и типа «вакансия–межузлие» соответственно.

Путем исключения n_i

_ toy к to =-------, к = т-------Т""

^Р 1 ^{+ в} V        ^(в i ^{+ в} V ) /cl

( to , к - безразмерные величины частоты и волнового числа, соответственно) получаем в следующем виде (черта опущена):

to + i ^— a 7 ( 1 + a 2 )( 1 + a 3 ) к to — to J —

— а з a 7 ( 1 + a 2 ) к ⁴ to² — ( 1 + a 7 ( a 2 + a 3 ) ) к ² to² —

( a ₂ — a₄a ₅) ₂

⁴ to ² +

( 1 + a ₂ )

+ i a 7 ( 1 + a ₂ )( 1 + a ₃ ) к ⁴ to

—

^a 1 ( 1^{+ a} 6 )

1 + a ₂

—

1 к ² to +

+ a 3 a 2 ( 1 + a ₂ ) ² к ⁶ + a 7 ( a ₂ + a 3 — a 1 ( a 3 + a 6 ) ) к ⁴ +

( a ₂ — a ₄ a ₅ — a 1 ( a ₂ + a 6 — a ₄ — a ₅ a 6 ) ) ( 1 + a ₂ ) 2

где безразмерные параметры имеют вид

Г 2 ) q„ Q„ ^E V a, = X +— ц —---

¹ I 3 Jp c l в у

a = ₽.

, ² в V ’

a ₃

к ² = 0,

- 1 f дnV     5U п д2 nV  R ni --' q ' DV - - вVn вiV ( дt      дx       дx

. - в у _n _ в

⁴ в v ’ ⁵ в у ’

Q, a₄ =---- , a, ⁶ Q v

= D l

D V , e V D V

c l ²

.

система (1)–(3) сводится к системе двух уравнений

д ² U д t1

+

X +— ц

T-—f I	c l —	Гл 2 V X+ 3 ц	3 q E Q i У PP ,V	)д2 U ") д x 2 +
X +	2 3 - ц	11 fa —	в V Q i	V n v
	3 У	ц v	в iV	J д X
|_Q	■ д2	n V - + f X +	2 3 ц	Q D v д 3 n v =
1 pp iv д x д t V			3 J	рв у д x 3

0,

^д n V      гл о п \^д n V        о \ n n V

-( » V o , ^+в i D V ли ■ ^в V )^

- (Dv+ Di )f-nV:+ did- "vv + дx д tд ди

+q Е(Ру — в)— q е дx     дx д t

Все параметры положительны, кроме двух a 1 <  0, a 6 <  0 .

В комплексном дисперсионном уравнении (6) волновое число должно быть комплексным к = к 1 + ik ₂ [33], где k ₁ и k ₂ – действительная и мнимая части волнового числа. С учетом этого обстоятельства продольное перемещение запишется в виде

U = U0 exp (к2 x) exp (ito t — ik1 x), здесь k1 и k2 характеризуют распространение и затухание волны соответственно при фиксированном значении частоты.

д г

⁺ q е Di _я з ^{+ (e} i ^e V ^{— в} iV ^в Vi ) n V = ^0. д x ³

2. Среда с одним типом точечных дефектов

В систему дифференциальных уравнений (4), (5) подставляем решение в виде монохроматических волн с произвольными амплитудами U ⁰ , n_V ⁰ :

Рассмотрим сначала два более простых частных случая, если в материале имеет место только один тип точечных дефектов: либо вакансии, либо межузлия. Система (1)–(3) будет иметь вид:

U = U ⁰ exp ( i to t — ikx ) ,

д ² U — ₂ д 2 и д t ² c l д x ²

n_v = n V exp ( i to t — ikx ) ,

f 2 ) ^Q j ^д n j — X +ц

I 3 J p

^d n,     d U     5 ² n j

— = qe—+d, —г - в n, dt       dx       dx2

( j = V и j = i в системах с вакансиями и межузлиями соответственно).

Комплексное дисперсионное соотношение (6) упростится ( a ₂ = 0, a 3 = 0, a 4 = 0, a 6 = 0):

m 3 - i ( 1 + a 7 k ² ) © ² - k ² © + i ( a 7 k ⁴ + ( 1 - a 1 ) k ² ) = 0, (7)

( 2 ) q П,        в ,D, где ax = 1 X + —ц 1^a7 =^~ (j = V, i).

I ³ Jp C l ^в j            C l

Раскладывая волновое число и разделяя действительную и мнимую части дисперсионного уравнения (7), получим систему

to + 2a7kik2© — (k1 — k2 )©-

- 4 a ₇ k³ k ₂ + 4 a ₇ k 1 k ₂ ³ — 2 ( 1 — a 1 ) k 1 k ₂ = 0,

( 1 + a 7 ( k 1 - k 2 ) ) © + 2 k_xk 2 ©-

- a7 (k4 + k4) + 6a7k12k22 - (1 - a1)(k2 - k22) = 0.

При решении системы (8) ограничимся рассмотрением волновых чисел с положительной действительной частью. Дисперсионные кривые k1 (©), k2 (©) изображены на рис. 1. Одна пара ветвей (k1, k2) (рис. 1, 1) имеет асимптоты в виде наклонной k1 = ©, исходящей из начала координат, и горизонтальной k2 = 0 прямых. Другая пара ветвей (рис. 1, 2) ограничена частями квад ратичной параболы k12 = ± — (рис. 1, короткий ,         2a7

штриховой пунктир).

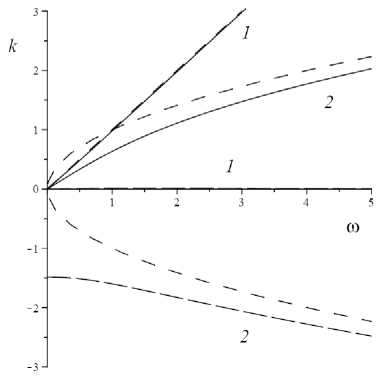
Рис. 1. Зависимости k 1 ( © ) (сплошная линия), k ₂ ( © ) (длинный штриховой пунктир)

Fig. 1. Dependences k ₁ ( © ) (solid line), k ₂ ( m ) (long dash line)

Распространяющейся волне соответствует коэффи- ^k циент затухания у = —, принадлежащий интервалу k 1

- 1 <у< 1. Только у одной пары ветвей ( k 1 , k ₂ ) этот коэффициент лежит в указанных пределах ( у , ^ 0, |у₂| >  1). Для вакансий коэффициент затухания положителен ( Y 1 >  0), для межузлий - отрицателен ( у 1 <  0) (рис. 2).

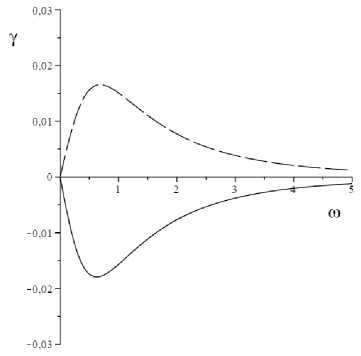
Рис. 2. Зависимость у ( © ) при различных значениях параметра a 1 : a 1 <  0 (штриховой пунктир), a 1 >  0 (сплошная линия)

Fig. 2. Dependence у ( © ) at various values of parameter a 1 : a 1 <  0 (dash line), a 1 >  0 (solid line)

Отследить динамику одной ветви (соответствующей распространяющейся волне) дисперсионной кривой k 1 ( © ) при изменении параметров a 1 , a ₇ позволяет разность этой ветви кривой со своей асимптотой. Рассмотрим функцию k 1 ( © ) = k 1 ( © ) - © . Влияние параметра a 1 на поведение кривой k 1 ( © ) показано на рис. 3. На рис. 4 изображены зависимости k 1 ( a ₇ ) , характерные для низких и высоких частот.

В области низких частот видно наличие ярко выраженной дисперсии (см. рис. 3). При любых значениях частоты: k 1 <  0 при a 1 <  0 и k 1 >  0 при a 1 >  0 .

Зависимость k 1 ( © ) от параметра a 1 монотонная: при увеличении абсолютного значения параметра кривая сдвигается в сторону увеличения абсолютных значений k 1 . Зависимость k 1 ( © ) от параметра a ₇ монотонная (убывающая при a 1 >  0 и возрастающая при a 1 <  0) в области низких частот и немонотонная в области высоких частот (см. рис. 4). При увеличении значения параметра a ₇ кривая k 1 ( © ) сдвигается сначала в сторону увеличения, затем в сторону уменьшения абсолютных значений k 1 ( © >>  1 ).

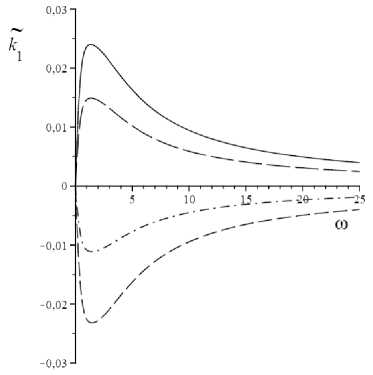
Рис. 3. Зависимость к ( го ) при различных значениях параметра a_i : а р) (короткий штриховой пунктир), a® (штрихпунктир), a ^{( 3 )} (длинный штриховой пунктир), a i⁴ (сплошная линия);

a ⁽¹) < а^й< 0 < а^№< a^W а^М = ИI а⁽³) > U²⁾I a i . a i       . . a i       . a i , a i a i , a i          a i

• Fig. 3.    Dependence k ( го ) at various values of parameter a _i : a p) (dash line), a^ (dash-dot line), a ^{( 3 )} (long dash line), a (^{4 )} (solid line)' a ( i ) < a^M< 0 < a^№<  a^w a^w = HI a^№ > |_ti(²) nue); a i <  a i < <  a i <  a i , a i — a i , a i >  a i

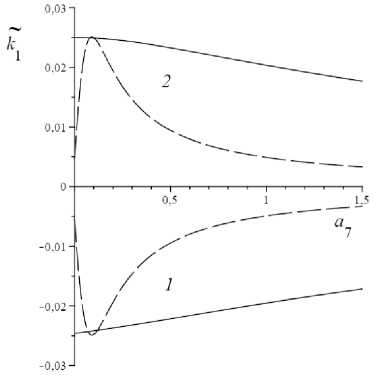
Рис. 4. Зависимость k _i ( a 7 ) при фиксированном значении частоты го и различных значениях параметра a _i: го <  i (сплошная линия), го >>  i (штриховой пунктир) и a _i <  0 ( 1 ), a _i >  0 ( 2 )

• Fig. 4.    Dependence k_i ( a 7 ) at fixed frequency value го and various values of parameter a _i: го <  i (solid line), го >>  i (dash line) and a _i <  0 ( 1 ), a _i >  0 ( 2 )

го

Зависимости фазовой v _h — — k 1

и групповой

v gr

d го dk1

скоростей изображены на рис. 5. Для скоро- стей в средах с вакансиями и межузлиями на всем интервале частот выполняются неравенства vph > vgr и vph < vgr соответственно. На низких частотах скорости близки к значению v0 — ^i - ai , а на высоких - близки к единице (v„ ^ i). Причем, если дефектами являются вакансии, то v0 > v„, а если дефектами являются ме-жузлия, то v0 < v„ .

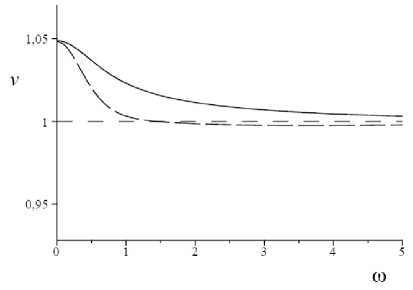
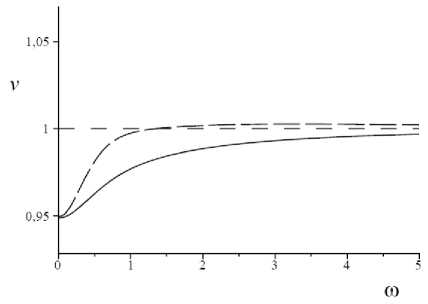
Рис. 5. Зависимости v_ph ( го ) (сплошная линия) и v gr ( го ) (длинный штриховой пунктир) при различных значениях параметра a _i: a _i <  0 ( a ), a _i >  0 ( b )

• Fig. 5.    Dependences v_ph ( го ) (solid line) and v gr ( го ) (long dash line) at various values of parameter a _i : a _i <  0 ( a ), a _i >  0 ( b )

• 3.    Среда с двумя типами точечных дефектов

На низких частотах (см. рис. 5) очевидно, так же, как и на рис. 3, наличие дисперсии. В средах с вакансиями наблюдается нормальная дисперсия, в средах с межузлиями – аномальная дисперсия.

Рассмотрим теперь более сложный – общий случай, если в материале одновременно имеют место оба типа точечных дефектов: вакансии и межузлия. По-прежнему считаем, что волны бегут в положительном направлении оси x ( k_i >  0).

По сравнению с предыдущим случаем, где у дисперсионной кривой две пары ветвей (из них только одна соответствует распространяющейся волне со слабым затуханием, к 2 ^ 0), здесь у кривой присутствует еще одна пара ветвей к 1 ( ю ) , к 2 ( ю ) , которая при определенных значениях параметров системы может соответствовать распространяющейся волне, имеющей постоянное ненулевое затухание.

Действительные ветви дисперсионной кривой (6) имеют три асимптоты: одна прямая и две квадратичные параболы с вершинами в начале координат ю = к1, ю = 2 a 7 (1 + a 2) к2, ю = 2 a 3 a 7 (1 + a 2) к2 .

Одна из трех ветвей зависимости к 1 ( ю ) имеет отсечку по волновому числу, если параметры системы удовлетворяют неравенству

• - a 1 a 4 - a ₂ - a 1 a 5 a 6 + a 1 a 6 + a 1 a ₂ + a 4 a 5 >  0, (9)

левая часть которого не зависит от параметров a ₃ , a ₇ .

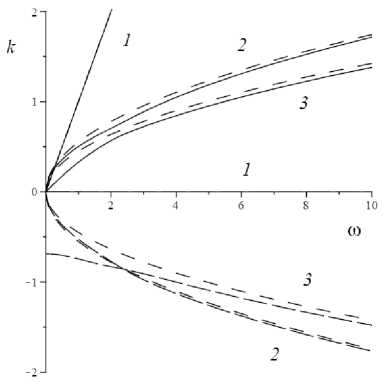
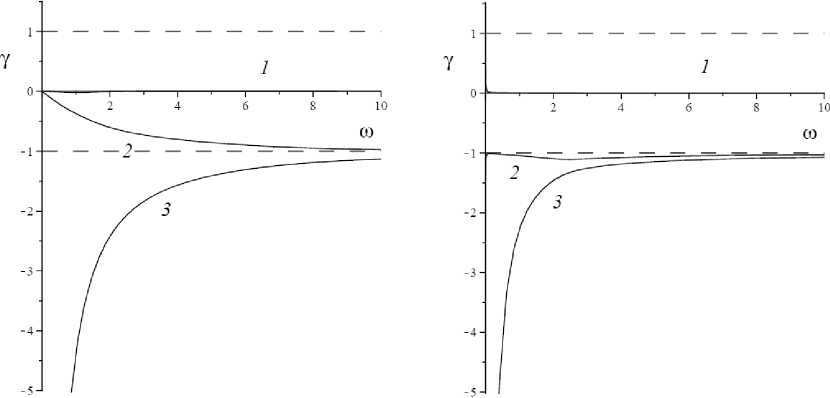
Соотношение параметров системы качественно влияет на вид дисперсионных кривых (рис. 6). Цифрами на рисунке условно пронумерованы пары ветвей (к1, к2). Соответствующие зависимости коэффициента затухания у1- у3 изображены на рис. 7. Асимптоты на рисунках, как и прежде, отмечены коротким штриховым пунктиром.

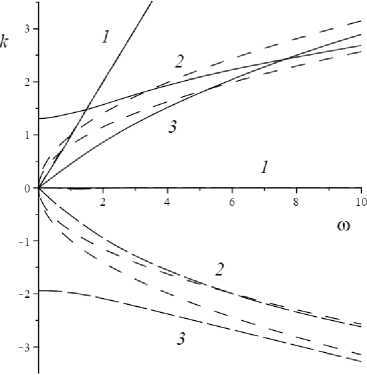
Рис. 6. Зависимости к 1 ( ю ) (сплошная линия), к ₂ ( ю ) (длинный штриховой пунктир) при выполнении ( a ) и невыполнении ( b ) условия (9)

b

Fig. 6. Dependences к ₁ ( ю ) (solid line), к ₂ ( ю ) (long dash line) when ( a ) is met and condition (9) is not met ( b )

а                                                   b

Рис. 7. Зависимость у ( ю ) (сплошная линия) при выполнении ( a ) и невыполнении ( b ) условия (9)

Fig. 7. Dependence у ( ю ) (solid line) when ( a ) is met and condition (9) is not met ( b )

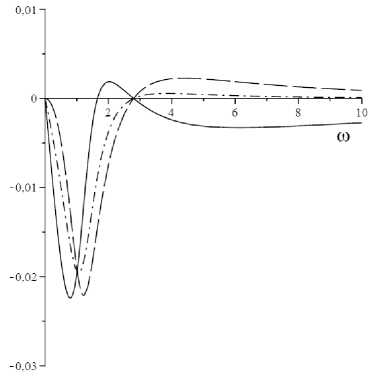
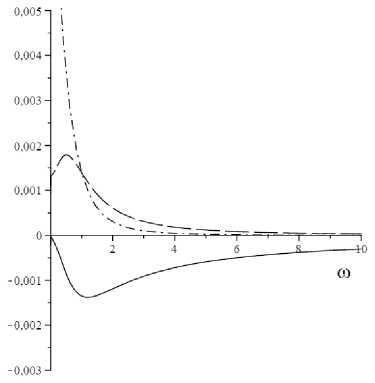
Рис. 8. Зависимости к 1 ( го ) (сплошная линия), к 2 ( го ) (длинный штриховой пунктир) и у ( го ) (штрихпунктирная

b

линия) при выполнении ( a ) и невыполнении ( b ) условия (9)

• Fig. 8.    Dependences к ₁ ( го ) (solid line), к 2 ( го ) (long dash line) and у ( го ) (dash-dot line) when ( a ) is met and condition (9) is not met ( b )

  

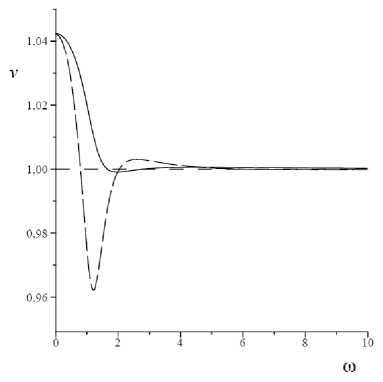
  Рис. 9. Зависимости v ph ( го ) (сплошная линия) и v gr ( го ) (длинный штриховой пунктир) при выполнении ( a ) и невыполнении ( b ) условия (9)

  
  
  

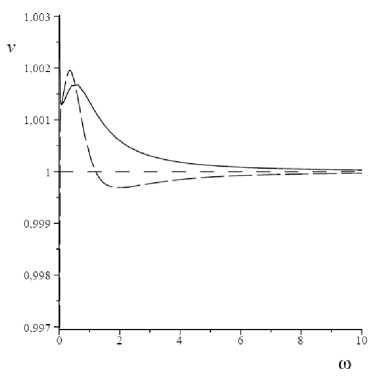
  b

  
  

• Fig. 9.    Dependences v ph ( го ) (solid line) and v_gr ( го ) (long dash line) when ( a ) is met and condition (9) is not met ( b )

Отсечка по волновому числу k ₁ , наблюдаемая на рис. 6, a , отсутствует на рис. 6, b .

При справедливости неравенства (9) на низких частотах может существовать еще одна продольная волна ( - 1 2 <  1), быстро затухающая в процессе распространения. Если параметры системы не удовлетворяют неравенству (9), то на всем интервале частот в среде распространяется только одна продольная волна ( Y 1 ^ 0), как и в предельных случаях (с одним типом точечных дефектов).

Параметры a ₃ и a ₇ не влияют на существование второй низкочастотной волны.

Зависимости к 1 ( го ) , к 2 ( го ) и у ( го ) распространяющейся волны представлены на рис. 8.

Из анализа к ( го ) следует, что кривая к₁ ( го ) в основном лежит ниже своей асимптоты (см. рис. 8, a ). Кривые к 2 ( го ) и у ( го ) меняют знак. Величины к 1 и к 2 разных знаков на низких и одного знака на высоких частотах. На низких частотах по мере распространения волны ее амплитуда уменьшается (волна затухает), аналогичное поведение наблюдается в однотипных средах с межузлиями. На высоких частотах амплитуда волны увеличивается (волна усиливается). Увеличение амплитуды волны типично для сред с вакансиями.

При нарушении неравенства (9) на всем интервале частот k ₁ и k ₂ имеют один знак.

Кривые фазовой и групповой скоростей показаны на рис. 9.

Кривая групповой скорости расположена как ниже, так и выше кривой фазовой скорости (см. рис. 9, a ). На низких и высоких частотах расположены участки с нормальной дисперсией, заключающие между собой участок с аномальной дисперсией.

На высоких частотах в обоих вариантах имеется нормальная дисперсия.

Очевидно, что если коэффициенты диффузий дефектов равны ( a ₃ → 1 ), то асимптоты – параболы дисперсионной кривой (6) совпадают. Кривые фазовой и групповой скоростей имеют одну точку пересечения. На низких частотах проявляется нормальная дисперсия, на высоких – аномальная.

Заключение

Моделируемая среда такова, что в отсутствие каких-либо дефектов имеем классическую упругую среду, продольная волна в которой распространяется без дисперсии и затухания. Точечные дефекты способствуют