Дисперсионные характеристики плоских продольных упругих волн, распространяющихся в пористой жидконасыщенной среде с полостями
Автор: Айзикович С.М., Ерофеев В.И., Леонтьева А.В.
Статья в выпуске: 4, 2016 года.
Бесплатный доступ
Многие сплошные на первый взгляд среды обладают многочисленными микропорами, которые содержат или не содержат жидкость. Эти поры гораздо меньше макроскопических размеров среды, но больше атомных или молекулярных размеров. Такие модели пористой среды, как модель грунта, широко применяются в геофизике. Этой моделью объясняется распространение жидкости (нефть, вода) через грунты. Такой моделью пользуются и в биологии, в частности, при описании протекания жидкости через растения, например древесину. В последние годы созданы искусственные пористые материалы, которые широко применяются в быту, в технике и других областях человеческой деятельности. Внастоящей работе рассматривается распространение плоских продольных волн в пористой жидконасыщенной среде с полостями. Предполагается, что диссипацией энергии волны в среде можно пренебречь. Изучается поведение линейных волн в полостно-пористых средах. Как известно, в пористой среде (среде Био) могут распространяться две продольные волны: одна медленная и одна быстрая. В нашей задаче распространяются три продольные волны: две волны, как в среде Био, и одна волна за счет полостности среды. Если бы в среде не было ни пор, ни полостей, то распространялась бы одна быстрая волна. Исследование поведения линейных волн проводится путем получения и анализа дисперсионного уравнения, фазовой скорости и групповой скорости, характеризующей перенос энергии волны. Для определения степени выраженности дисперсии рассматривается плотность спектра частот.В работе построены и проанализированы дисперсионные зависимости для рассматриваемой системы. Найдены области сильной и слабой дисперсии, области нормальной и аномальной дисперсии при конкретных значениях параметров системы.
Линейная волна, продольная волна, упругая волна, пористая среда, двухфазная среда (среда био), полости, дисперсионное соотношение, фазовая скорость, групповая скорость
Короткий адрес: https://sciup.org/146211639
IDR: 146211639 | УДК: 534.1 | DOI: 10.15593/perm.mech/2016.4.10
Текст научной статьи Дисперсионные характеристики плоских продольных упругих волн, распространяющихся в пористой жидконасыщенной среде с полостями
PNRPU MECHANICS BULLETIN
Впервые модель, состоящая из твердого каркаса с многочисленными связанными между собой порами, была предложена в сороковые годы XX в. Морисом Био (Maurice A. Biot) [1], поэтому такие среды часто называют средами Био. В работе [1], как и в последующих работах цикла [2–8], пористость материала предполагалась постоянной, что не соответствует физической реальности. Несмотря на это допущение, работы М. Био, как пионерские, несомненно, внесли большой вклад в теорию пороупругости, в частности, в них выявлен новый физический эффект – существование двух продольных волн – быстрой и медленной.
Формула изменения пористости при малых деформациях впервые предложена Я.И. Френкелем и опубликована в статье [9], являющейся второй классической работой в этой области.
В работе Л.Я. Косачевского [10] последовательно изложена линейная теория деформирования двухфазной среды, учитывающая результаты работ М. Био и Я.И. Френкеля, получено выражение для энергии, коэффициенты которого зависят от таких параметров среды, как исходная пористость, коэффициент сжимаемости и др.
Развитие основных положений механики и физики пористых материалов содержится в монографиях [11–15].
Вопросам распространения волн в пористых материалах посвящены, в частности, работы [16–25].
С 1999 г. регулярно проводятся крупные многопрофильные международные конференции по механике пористых материалов («Poromechanics») [26–30].
В монографии [31] отмечается, что во многих природных средах (туф, пемза и т.д.), а также в искусственных композитах в сочетании с пористостью встречаются многочисленные, часто заполненные жидкостью, полости. Таким образом, изучение пористополостных твердых сред представляет большой интерес с точки зрения теории и практики.
1. Постановка задачи
Пусть имеется полубесконечная или в форме слоя среда Био, в которой существуют полости с жидкостью. Считается, что поры цилиндрической формы, а полости – шарообразной. Под действием упругой волны полости будут колебаться, оказывая, в свою очередь, влияние на распространение волны.
Уравнения, описывающие деформацию пористой жидконасыщенной среды с полостями, наполненными жидкостью, в лагранжевых координатах приведена в [31]. В этой системе считаем, что вязкость отсутствует, а всеми типами нелинейности пренебрегаем. Рассматриваем плоскую продольную волну, распространяющуюся вдоль оси x 3 . Ограничиваясь вторыми производными и линейными членами, получим следующую систему, описывающую распространение плоской продольной волны в среде Био:
Р 11
d 2 u 3 dr
+ Р 12
d 2 v 3 d r
+ 2.'' ' u - Q ' + N ( X , + 2 n)| v = 0, о x3 о x 3 о x 3
* p 22
d 2 v 3 dl'
+ p 12
5 2 u 3 df-
Q s2uu i. - R ^
d x 3 d x 3
= 0,
d 2 v , 2
--- + ®sv -
5 1 2 5
4 n r2
P o
(X2+2ц) 'u
V d x 3
-
1 d
Nv +-- Qvv. + RuA = 0,
J 5x3( 3 3)
где u3 , v3 ‒ перемещения твердой и жидкой фаз соответственно вдоль направления оси x3; v - объем полости, возмущенной волной; p11, p22 - эффективные начальные плотности массы твердой и жидкой фазы соответственно; p11 = p1 -p12, p22 =p2 -p12, p12 < 0 , p1, p 2 - массы твердой и жидкой фазы соответственно; p12 - присоединенная плотность массы; X2, ц - коэффициенты Ламе; Q, R - известные коэффициенты, характеризую- щие жидконасыщенную среду, их значения даны в [10]; N ‒ количество полостей в единице объема; to5 - резонансная частота, to2 =(3у^0 + 4^)/(r22p0); r2 - радиус полостей;
p 0 - плотность твердой фазы; p 0 - начальное давление в жидкости внутри полости; у -показатель адиабаты жидкости.
2. Дисперсионные свойства системы
Для получения дисперсионного уравнения подставляем в систему линейных дифференциальных уравнений (1) решение в виде монохроматических волн:
u 3 = u 30 exp (ito t - ikx), ' v3 = v30 exP (iю t — ikx), v = v0 exp (ito t - ikx), группируем слагаемые при амплитудах u3 , v3 , v , выписываем соответствующий определитель и приравниваем его нулю. Раскрывая определитель, получаем дисперсионное соотношение
-
-p0pto6 +(p(poto 2 + n ) + p0 qik 2 )to4 +
2242224 (2)
+ ((-p0tosq1 + nq2)k2 +p0qk) to2 -(p0tosq + nR)k4 = 0, где для сокращения записи введены обозначения p = p11p22 -p22, K = ^2 + 2P , q =p11R + p22 K- 2p12Q , q 2 =p12Q-(p11 —p22 ) R , q = Q 2 -KR , n = 4ПГ2NK .
Выбрав в качестве характерных величин частоты и волнового числа резонансную частоту и отношение резонансной частоты к скорости распространения упругой продольной волны в воде
-
_ to T k
to = —, k = —-, tos tosjc где to , k - безразмерные величины частоты и волнового числа соответственно, получаем дисперсионное соотношение (2) в безразмерном виде (черта опущена):
to6 -(1 + a1 + a2k2 )to4 +((a2 - a1 a4) k2 - a3k4 )to2 +(a3 + a1 a5) k4 = 0, где ai (i = 1...5) - безразмерные коэффициенты:
n q1 q q2
-
a 1 = 2 , a 2 = 2" , a 3 = 4 , a 4 = 2 , a 5 = T .
-
p0to s pc pc pcp
Уравнение (3) имеет шестой порядок по to и четвертый порядок по k . Дисперсионные кривые имеют три ветви, две из которых исходят из начала координат и одна из точек ( 0, ± 1 + a 1 ) . Для безразмерных частоты и волнового числа получены следующие характеристики при различных значениях параметра a 5 уравнения (3) (рис. 1).
Из рисунков видно, что внутренние ветви, теряя гладкость, стремятся к нулю. В начале координат происходит четкое разделение дисперсионных кривых на три пары, из которых одна начинает вытягиваться вдоль оси x , а другая меняет форму, принимая вид ломаной, касается третьей. В точке касания происходит разрыв дисперсионной кривой. При дальнейшем увеличении параметра одна ветвь кривой исчезает с действительной плоскости, а две другие, разделившись на две общие части, продолжают отдаляться друг от друга.
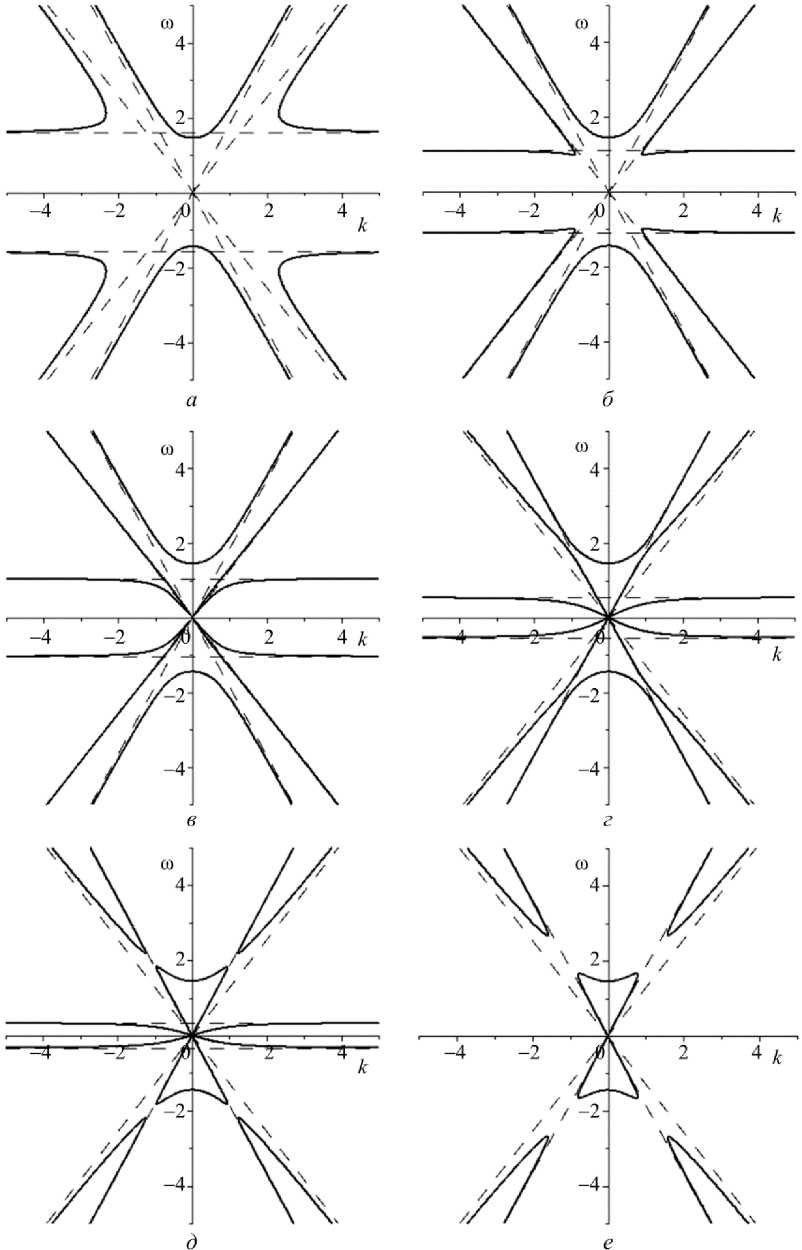
Рис. 1. Динамика дисперсионной кривой при изменении параметра a 5 , a 51 ) ( a ) < a 2 ) ( б ) < a 53 ) ( в ) < a 54 ) ( г ) < a 55 ) ( д ) < a 56 ) ( е )
Fig. 1. Dynamics of disperse curve depending on alterations of parameter a 5 , a 51 ) ( a ) < a 52 ) ( b ) < a 53 ) ( c ) < a 54 ) ( d ) < a 55 ) ( e ) < a 56 ) ( f )
Дисперсионная кривая, заданная уравнением (3), имеет две горизонтальные и четыре наклонные проходящие через начало координат асимптоты to = ± b± к, to = ± 1 + a1a5, a3
где b ± =
a 2 + 4 a 3 . Вертикальные асимптоты у кривой отсутствуют.
Подставляя v ph = to в (3), находим зависимость фазовой скорости и волнового числа:
v ph
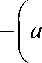
1 + a , k 2
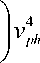
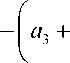
a , a 4 — a 2 ]
k 2 )
2 v ph
a 3 + a , a 5
+ k 2
= 0.
При к ^ 0 одна ветвь кривой уходит в бесконечность, а две другие принимают значения vph =
a 2 — a , a 4
a 2
2 a 1 a 4
^ 2 ( 1 + a , ) К 2 ( 1 + a , )
+ a 3 + a , a 5 1 + a ,
У кривых фазовых скоростей, определяемых зависимостью (4), наклонные асимптоты отсутствуют. Но есть шесть горизонтальных асимптот, две из которых нулевые и две – вертикальные нулевые асимптоты: vph = ± b ± , vph = 0 , к = 0 .
Дифференцируя (3) по k и подставляя vgr
d to dk
получаем связь групповой скорости
и волнового числа:
v gr
к ( a 2 to 4 + ( 2 к 2 a 3 + a , a 4 — a 2 ) to 2 — 2 ( a 3 + a , a 5 ) к 2 )
to (— 3 to + 2 ( a 2 к + a , + 1 ) to + a 3 к + ( a , a 4 — a 2 ) к )
В (5) to определяется из дисперсионного уравнения (3). При к ^ 0 одна ветвь кривой групповой скорости устремляется в начало координат, а две другие принимают соответствующие значения фазовых скоростей. Кривые групповых скоростей, определяемые зависимостью (5), имеют шесть горизонтальных асимптот, из которых две нулевые: vgr = ± b ± , vgr = 0 . Наклонные и вертикальные асимптоты отсутствуют.
Рассмотрим варианты расположения трех веток дисперсионной кривой, которые показывают характерное поведение системы. В силу симметрии графиков функций (3), (4), (5) относительно осей координат достаточно их изображения в первой четверти. Для удобства анализа представим зависимости to(к), vph (к), vgr (к) в одних осях (рис. 2).
На рисунке сплошной линией показана зависимость to(к), длинным пунктиром - vph (к), штрихпунктиром - vgr (к)
коротким пунктиром отмечены асимптоты кривых. Из рисунка видно, что первая ветвь дисперсионной кривой зарождается на частоте to = to0 = 0. При небольших волновых числах (к < 1), т.е. для длинных волн (X >> 1), час тота стремится к значению to = b + к, на бесконечности частота стремится к значению to = b- k . Фазовая и групповая скорости соответствующих ветвей стремятся к значению v = b- с разных сторон. Вторая ветвь дисперсионной кривой зарождается на частоте to = to0 ^ 0. На бесконечности частота стремится к значению to = b + k . Соответствующие ветви кривых фазовой и групповой скорости стремятся к общей асимптоте vph = vr = b+ с разных сторон. Третья ветвь дисперсионной кривой зарождается на частоте to = to0 = 0.
На бесконечности частота стремится к значению to = 1 + a 1 a 5 , значения фазовой и груп- a 3
повой скоростей стремятся к нулю. На промежутке ( 0, +^ ) групповая скорость меньше фазовой скорости, что говорит о нормальной дисперсии при выбранных значениях параметров системы.
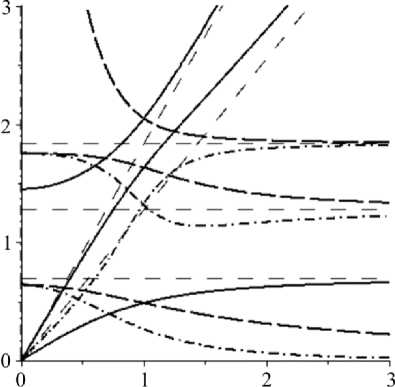
Рис. 2. Зависимости to ( k ) , v ph ( k ) , v r ( k )
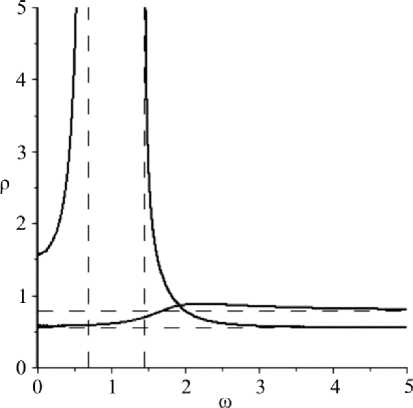
Рис. 3. Плотность спектра частот p ( to )
Fig. 3. Density of spectral frequencies p ( to )
Fig. 2. Dependences of to ( k ) , v ph ( k ) , v r ( k )
Плотность спектрального распределения [32] позволяет определить промежутки частот, на которых проявляется явление дисперсии волн. Вычисляется плотность спектрального распределения по следующей формуле:
dk
p( to) = cons' t----, d to где константу можно выбрать равной единице, так как на качественный вид кривой она не повлияет. С точностью до множителя плотность является величиной обратной к групповой скорости. Из графика плотности спектра частот несложно определить, при приближении к каким частотам спектр становится непрерывным. Плотность спектрального распределения для каждой ветви дисперсионной кривой изображена на рис. 3.
Из рисунка видно, что спектр частот сгущается и становится непрерывным при to ^ 1 + a1 a5 - 0. Спектр собственных частот to e a3
a^ a 5
0 1 + -1-5-
\ a 3 J
. Значит, для медленной
волны (на рис. 1 – третья ветка) дисперсия проявляется на высоких частотах. Также из рис. 3 видно, что спектр частот становится непрерывным при ю ^ ^Х + a1 + 0. Спектр собственных частот лежит в диапазоне (^ 1 + a1 ,+<*>). Значит, у быстрой волны, которая возникает из-за полостности среды, дисперсия проявляется на низких частотах. Небольшое увеличение плотности спектрального распределения у первой ветки дисперсионной кривой, соответствующей быстрой волне, возникшей в результате пористости среды, соответствует незначительной дисперсии. Спектр собственных частот ю е [0,+^ ).
При изменении одного из параметров дисперсионная кривая претерпевает разрыв.
Значение параметра a5 = a*s, a*s = a3 +(a2 + a4 )b±2, при котором происходит разрыв диспер сионной кривой. Значение координат точки разрыва (к, ю) можно найти из условия пере- сечения кривой (3) со своей асимптотой или из условия пересечения двух веток дисперсионной кривой. Дисперсионная кривая после разрыва представлена на рис. 4.
Дисперсионная кривая (рис. 4) по-прежнему имеет три ветви, но их вид качественно изменился. Появилась ветка с двумя частотами зарождения и «свободная» ветка. На бесконечности кривая сохранила линейную асимптотику. Участки первой и второй веток дисперсионной кривой «перепрыгнули» асимптоту ю = b + к. Кривая групповой скорости приобретает асимптоты, аналитический вид которых не удается отыскать. Дисперсия приобрела аномальный характер (рис. 4) на тех участках дисперсионной кривой, которые сменили расположение относительно асимптоты ю = b + к .
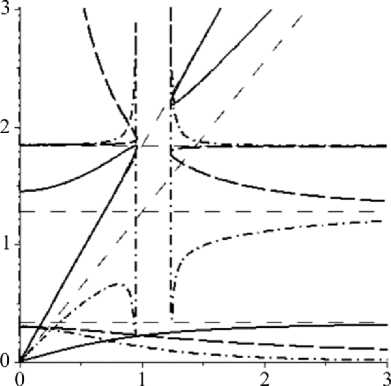
Рис. 4. Зависимости ю ( к ) (сплошная); vph ( к ) (длинный пунктир); vgr ( к ) (штрихпунктир) Fig. 4. Dependences of ю ( к ) (solid line); vph ( к ) (longdashedline); v gr ( к ) (dot-dash line)
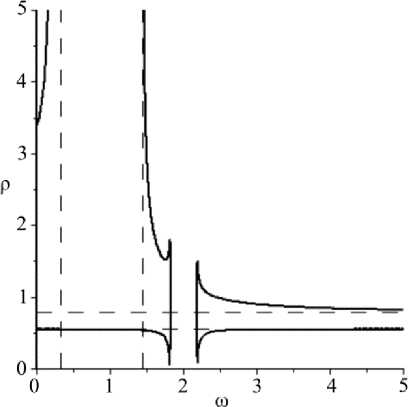
Рис. 5. Плотность спектра частот Fig. 5. Density of spectral frequencies
Спектр частот (рис. 5) становится непрерывным при стремлении частоты к четырем aa критическим частотам: ю > 1 + - 0, ю^ ^1 + a1 + 0, и частотам, вблизи которых a3
дисперсионные кривые приобретают пики.
Заключение
Таким образом, в статье показано следующее:
-
1. В среде распространяются три продольные волны, две – быстрая и медленная за счет жидконасыщенной пористой среды и одна (на рис. 2. вторая ветка) – за счет полост-ности среды. При отсутствии полостей в среде дисперсионная кривая имела бы две ветви (как в среде Био): первая, которая всегда присутствует на плоскости ( к, ю ) , и третья, которая появляется вследствие пористости среды.
-
2. Волны, распространяющиеся в пористой среде с полостями, обладают значительной дисперсией. Причем быстрые волны обладают дисперсией в области низких частот, а медленные волны – в области высоких частот.
-
3. При фиксированных параметрах в системе может наблюдаться аномальная дисперсия на двух участках дисперсионной кривой. Существенная дисперсия проявляется вблизи четырех частот. У медленной волны на высоких частотах. У быстрой волны, которой соответствует «свободная» ветка дисперсионной кривой, дисперсия проявляется на низких частотах, а у быстрой волны, которой соответствует ветка с двумя частотами зарождения, – на частотах в области пика и в области ненулевой частоты зарождения.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 15-19-10056).
Список литературы Дисперсионные характеристики плоских продольных упругих волн, распространяющихся в пористой жидконасыщенной среде с полостями
- Biot M.A. General theory of three-dimentional consolidation//J. Appl. Phys. -1941. -Vol. 12. -No. 1. -P. 155-164.
- Biot M.A. Theory of elasticity and consolidation for a porous anisotropic solid//J. Appl. Phys. -1955. -Vol. 26. -No. 1. -P. 182-185.
- Biot M.A. General solution of the equations of elastisity and consolidation for a porous materials//Trans. ASME: J. Appl. Mech. -1956. -Vol. 23. -No. 1. -P. 91-96.
- Biot M.A. Theory of propagation of elastic waves in a fluid -saturated solid//J. Acoust. Soc. Amer. -1956. -Vol. 28. -No. 2. -P. 168-191.
- Biot M.A., Willis D.G. The elastic coefficient of theory consolidation//Trans. ASME: J. Appl. Mech. -1957. -Vol. 24. -No. 3. -P. 594-601.
- Biot M.A. Mechanics of deformation and acoustical propagation in porous media//J. Appl. Phys. -1962. -Vol. 33. -No. 10. -P. 1482-1498.
- Biot M.A. Generalized theory of acoustic propagation in porous dissipative media//J. Acoust. Soc. Amer. -1962. -Vol. 34. -No. 1. -P. 1254-1264.
- Biot M.A. Variational langrangian thermodynamics of nonisotermal fin the strain mechanics of porous solid and thermomolecular diffusion//Int. J. Solids and Struct. -1977. -Vol. 13. -No. 6. -P. 579-597.
- Френкель Я.И. К теории сейсмических и сейсмоэлектрических явлений во влажной почве//Изв. АНСССР. Серия географическая и геофизическая. -1944. -Т.8, № 4. -С. 133-149.
- Косачевский Л.Я. О распространении упругих волн в двухкомпонентных средах//Прикладная математика и механика. -1959. -Т. 23, № 6. -С. 1115-1123.
- Механика пористых насыщенных сред/В.Н. Николаевский, А.Т. Басниев, А.Т. Горбунов, Г.А. Зотов. -М.: Недра, 1970. -335 с.
- Нигматулин Р.И. Основы механики гетерогенных сред. -М.: Наука, 1978. -336 с.
- Николаевский В.Н. Геомеханика и флюидодинамика с применением к проблемам газовых и нефтяных пластов. -М.: Недра, 1996. -477 с.
- Coussy O. Poromechanics. -Wiley, 2004. -312 p.
- Coussy O. Mechanics and Physics of Porous Solids. -Wiley, 2010. -282 p.
- Leclario F., Cohen-Tenou djv, Aguirre Puente Y. Extension of Boit’s theory of waves propagation to frozen porous media//J. Acoust. Soc. Amer. -1994. -Vol. 96. -No. 6. -P. 3753-3768.
- Быков В.Г. Сейсмические волны в пористых насыщенных породах. -Владивосток: Дальнаука, 1999. -108 с.
- Schanz M. Wave Propagation in Viscoelastic and Poroelastic Continua: A Boundary Element Approach. -Berlin: Springer, 2001. -170 p.
- Марков М.Г. Распространение волны Релея вдоль границы пористой среды, насыщенной неньютоновской жидкостью//Акустический журнал. -2005. -Т. 52, № 4. -С. 1-7.
- Марков М.Г. Распространение упругих продольных волн в насыщенной пористой среде со сферическими неоднородностями//Акустический журнал. -2005. -Т. 52. Приложение. -С. 132-139.
- Хоа Н.Н., Тарлаковский Д.В. Распространение нестационарных поверхностных кинематических возмущений в упругопористой полуплоскости//Механика композиционных материалов и конструкций. -2011. -Т. 17, № 4. -С. 567-576.
- Численное моделирование динамики составного пороупругого тела/Л.А. Игумнов, С.Ю. Литвинчук, Д.В. Тарлаковский, Н.А. Локтева//Проблемы прочности и пластичности. -2013. -Т. 75, № 2. -С. 130-136.
- Гранично-элементный анализ волн на упругом, пористом и вязкоупругом полупространствах/Л.А. Игумнов, А.С. Оконечников, Д.В. Тарлаковский, А.А. Белов//Проблемы прочности и пластичности. -2013. -Т. 75, № 2. -С. 145-151.
- Данг К.З., Тарлаковский Д.В. Действие на границу упругопористого полупространства с касательной диафрагмой нестационарной нормальной осесимметричной нагрузки//Механика композиционных материалов и конструкций. -2014. -Т. 20, № 1. -С. 148-158.
- Численно-аналитическое исследование динамики вязких пористо-упругих тел/Л.А. Игумнов, А.В. Аменицкий, А.А. Белов, С.Ю. Литвинчук, А.Н. Петров//Прикладная механика и техническая физика. -2014. -Т. 55, № 1. -С. 108-114.
- Poromechanics -A Tribute to Maurice A. Biot, Proceedings, Biot Conference on Poromechanics/J.-F. Thimus, Y. Abousleiman, A.H.-D. Cheng, O. Coussy, E. Detournay; eds. A.A. Balkema. -Rotterdam: Brookfield, 1998. -648 p.
- Poromechanics II/J.-L. Auriault, C. Geindrean, P. Royer, J.-F. Bloch, C. Boutin, L. Lewandovska; eds. A.A. Balkema. -Rotterdam: Brookfield, 2002. -955 p.
- Abousleiman Y.N., Cheng A.H.-D., Ulm F.-J. Poromechanics III/eds. A.A. Balkema. -Leidon, London, New York, Phyladelphia, Singapore, 2005. -828 p.
- Poromechanics IV/eds. Ling H.I., Smyth A., Betti R. -DEStech Publications. Inc., PA, USA, 2009. -1151 p.
- Poromechanics V/eds. Hellmich C., Pichler B., Adam D. -ASCE, 2013 (CD).
- Bagdoev A.G., Erofeyev V., Shekoyan A.V. Wave Dynamics of Generalized Continua. -Springer, 2016. -274 p.
- Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. -М.: Наука, 1984. -432 с.


