Диссипация кубита и концентрации алгебр Ли

Построить физическую теорию означает построить математический образ физической системы, под которой понимается любая ограниченная соответствующим образом область физического мира. Поэтому все физические теории имеют свою область применимости (область истинности). В классической механике наблюдаемыми физической системы являются вещественные бесконечно дифференцируемые функции координат и импульсов, а ее образ есть коммутативная алгебра вещественных гладких функций на фазовом пространстве [1]. В квантовой физике наблюдаемой, определенной предписанием способа ее измерения, отвечает линейный оператор в линейном пространстве. Математическим образом квантовой системы является, вообще говоря, некоммутативная алгебра операторов в линейном пространстве [1,2]. Эта алгебра генерируется некоторыми фундаментальными физическими величинами и определяющими соотношениями между ними.

Представление физических наблюдаемых операторами ставит проблему соотнесения этих математических объектов с экспериментальными данными, которые являются вещественными числами. Она решается введением понятия состояние квантовомеханической системы, которое описывается положительно определенным эрмитовым оператором р, Tr р = 1 — матрицей плотности. Среднее значение наблюдаемой A физической системы, находящейся в состоянии ρ , дается выражением < А >  = Tr ( Ар ) .

Динамика консервативной (изолированной) квантовой системы определяется унитарным оператором эволюции. Поэтому коммутаторы ее алгебры наблюдаемых не изменяются в процессе эволюции системы. Другая картина имеет место для неконсервативных (открытых) квантовых систем, эволюция которых уже не описывается унитарным оператором и, следовательно, алгебра наблюдаемых может изменяться в ходе эволюции системы. Изменение во времени матрицы плотности описывается преобразованием Крауса

р ( t ) = Л( t ) р (0) = £ _к E _k ( t ) р (0) E + ( t ) ,

£ к E k (t) E + ( t ) = 1 , (1)

или уравнением Линдблада [3, 4]

^р = - ~ [ H ,^р ] ⁺ ^ ( V k ^рV k - 2 { V k V k ,^р }) • к

Диссипативные процессы в открытых квантовых системах могут приводить к обнулению некоторых коммутаторов алгебры наблюдаемых, что интерпретируется как частичная потеря системой квантовых свойств, т.е. частичному переходу от квантового поведения к классическому (в отличие от предельного перехода при стремлении к нулю постоянной Планка ~ — > 0 , когда система становится полностью классической). Появляющиеся при этом коммутирующие наборы в алгебре наблюдаемых рассматриваются как классические переменные, возникающие в результате диссипации.

С другой стороны, в физике давно известен метод получения новых групп (алгебр) Ли путем обнуления всех или некоторых коммутационных соотношений между генераторами исходной группы (алгебры) Ли – это контракции групп (алгебр) Ли [5–7]. В работах [8, 9] диссипативные процессы в открытых квантовых системах анализируются с точки зрения контракций, как процедур, обнуляющих коммутаторы и произведения наблюдаемых системы и приводящих к изменению их алгебраических структур. В работе [10] также было отмечено, что при описании квантовых каналов кубита возникают формулы из теории контракций алгебр Ли.

В данной работе мы на нескольких простых примерах демонстрируем, что преобразования Крауса по сути являются преобразованиями контракций матрицы плотности ρ, как элемента алгебры Ли. Решения уравнений Линдблада, как для матрицы плотности ρ, так и для операторов наблюдаемых A, так- же могут быть записаны с помощью контракционных преобразований, если отождествить параметр контракции с экспонентой от времени е = e-Yt.

Сначала мы рассмотрим хорошо известные примеры каналов, разобранные в [9], и интерпретируем их с точки зрения контракций алгебр Ли. Далее, наоборот, мы берем из теории контракций алгебры su (2) две наиболее общие контракции и исследуем соответствующие им квантовые каналы. В заключении предлагается ли-алгебраическая интерпретация процессов декогеренции и диссипации.

1.    Преобразования Крауса и контракции

Матрица плотности кубита |^) = а| 0 ) + в1 1 ) Е C2 задается элементами алгебры Ли и (2)

_ 1          _ 1 / 1 + z x - iy \ р ~ 2 r S — 2 \ x + iy 1 — z / где r = (x,y,z), a = (Стх,сту,а), ai - матрицы Паули ax = ( 1 1 ) , Sy = ( i i\a2 = ( 1 -1 У

Для чистого состояния кубита x2 + y2 + z2 = 1 матрицу плотности ρ можно реализовать вектором ⃗r на сфере Блоха. Преобразования Крауса (1) задаются афинным отображением [11] вектора ⃗r r ^ M • r + c,

где M – действительная матрица, представимая в виде произведения M = O • S, O - ортогональная, а S – симметричная матрицы. Ортогональная матрица описывает унитарную эволюцию, сохраняющую сферу Блоха, а симметричная – неунитарные процессы диссипации, измерения, квантовый шум, эволюцию открытых систем. После диагонализации матрицы S , преобразование (4) может быть записано в виде [11]

c з( e i )

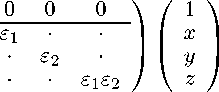
который возникает в теории контракций алгебр Ли.

При этом ε i имеют смысл контракционных параметров. Преобразования (5) проиллюстрированы на

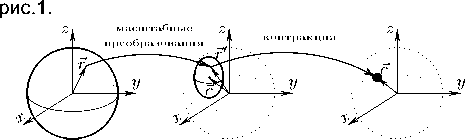
Рис. 1. Масштабные преобразования (4) при M = S переводят сферу Блоха в эллипсоид с центром, задаваемым вектором с , а предел e i —> 0 сжимает его в точку.

Fig. 1. Scale transformations (4) at M = S transform the Bloch sphere into an ellipsoid with the center given by the vector c , and the e i —> 0 limit compresses it to a point.

Напомним, что алгеброй Ли называется векторное пространство V с антисимметричной билинейной операцией [ , ] : V х V ^ V , удовлетворяющей тождеству Якоби

[[ A, B ] ,С ] + [[ B,C ] , A ] + [[ C, A ] ,B ] = 0 . (6)

Введем преобразования контракций как семейство линейных изоморфизмов алгебры Ли E ( e i ) : V ^ V , где e i е (0 , 1] - параметры контракции. Например, коммутационные соотношения алгебры su (2)

[ O x , O y ] = 2 iO z , [ O y , C z ] = 2 ic _x ,

[ O z ,O x ] = 2 ic y                 (7)

допускают преобразования Кэли-Клейна E ( e i ) генераторов [7]

E ( e i ) 5 =

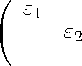
^OO y^x   =

ε 1 ε 2        σ z

ε ₁ σ _x ε 2 σ y ε 1 ε 2 σ z

, (8)

которые приводят коммутаторы (7) к виду

[ O x , O y ] = 2 iO z ,   [ O y ,O z ] = 2 ie 1 0 x ,

[ O z ,O x ] = 2 ie 2 O y .                 (9)

Возможны также преобразования генераторов диагональной матрицей с тремя независимыми параметрами E(ei) = diag(e1,e2,e3), и более общие недиагональные преобразования Салетана [6]. Устремление к нулю параметров εi в выражениях lim E- 1(ei)[E(ei) • A, E(ei) • B] = [A, B]    (10)

ε i → 0

определяет коммутаторы новых, неизоморфных исходной, алгебр Ли. Такая процедура называется контракцией и была определена в [5] как предел непрерывного сингулярного преобразования алгебр Ли. Позже было показано, что заменой ε _i на коммутативные нильпотентные образующие алгебры Пименова 1 1 = 1 2 = 0 , 1 1 1 ₂ = 1 ₂ 1 1 , можно определить контракцию без предельного перехода [7]. Преобразования E приобретают при этом схожий с (1) дискретный характер. Сравнивая (4),(5) и (8) приходим к выводу, что преобразования Крауса, соответствующие симметричной части матрицы M , можно интерпретировать как преобразования контракции E ( р ) элемента алгебры Ли ρ → ρ ^′

P* = 2 ^{(1 + E ( e} i ^{) O} ^ ⁵ ) = 2 ^{(1 + 5} • ^{E ( e} i ) ⁵ ) = ^{E (} P ) .

Таким образом, используя различные преоб- разования контракции, мы получаем простое описание неунитарных операторных сумм Крауса. Отме- тим, что пока мы не устремили ε к нулю, вращательная симметрия su(2) системы не меняется, а при e = 0 мы переходим к матрице плотности с новой симметрией, содержащей коммутирующие генераторы.

• 2.    Канал с переворотом фазы

Рассмотрим некоторые важные примеры однопараметрических преобразований Крауса для кубита вместе с соответствующими им решениями уравнений Линдблада и найдем их реализации на языке контракций. Определим набор матриц {Ek}

E о = v P i I , E y = VP 2 O y , P 1 + P 2 = 1 ,

E x

p 2 σ x ,

^√ p 2 σ z ^,

P i - P 2 = e.

Канал с переворотом фазы описывается преобразованиями Крауса (1) с матрицами E 0 и E z

P ^ P = E о pE + + E z pE + =

= 2 ( e(x + 5,) e(X - ?) ) = E(P) <13> и отображает чистое состояние, которому соответствует вектор (x,y, z) на сфере Блоха в смешанное состояние: исходного состояния с вероятностью p1 и с вероятностью p2 состояния, которому соответствует вектор (-x, -y, z). Сфера Блоха при этом дефор- мируется как показано на рис. 2.

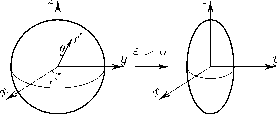
е >  0

Рис. 2. Деформация сферы Блоха в канале с переворотом фазы.

Fig. 2. Deformation of a Bloch sphere in a channel with phase reversal.

Преобразование ρ → ρ ^′ можно интерпретировать как преобразование контракции с E = diag( e,e, 1) , E ( x,y,z ) = ( ex,ey,z ) или на языке генераторов E ( O _x ,O _y ,o _z ) = ( eO x ,eO y ,o _z ) . Предел e ^ 0 дает алгебру Евклида для наблюдаемых и матрицу плотности

е ^ 0

р =2(1^{+ z} 1 - z)         (14)

с вектором Блоха r = (0 , 0 , z ) , z е [ — 1 , 1] , не меняющимся при преобразованиях Евклида в плоскости ( x,y ) (см. рис. 2).

Уравнение Линдблада (2), описывающее временную динамику кубита для канала с переворотом фазы, можно задать операторами H = 0 и V = ^γ ₂ σ 3 в виде

γ р = - 2(P - O3POз) .

Это уравнение приводит к динамической системе

.z = 0 , ic = - yx, г / = ^-Yy

с решением z = zо, x = e Ytxо, y = e Ytyо.     (17)

Эволюция

во времени матрицы плотности имеет вид

• 1    /      1 + z о       e ^Yt ( x о - iy о) \

• 2    \ e ^-Yt ( x о + iy о)       1 - z о      у ,

который, естественно, интерпретируется как контракционное преобразование, эквивалентное преобразованиям Крауса (13) после отождествления е = e ^—Yt . Очевидно, что при t ^ ж система стремится к состояниям (14).

Рис. 3. Эволюция матрицы плотности (18) по прямой.

Fig. 3. Straight line evolution of the density matrix (18).

Пользуясь равенством для нахождения среднего значения наблюдаемой A в состоянии ρ

Tr[ p ( t ) A ] = Tr[ pA ( t )] ,             (19)

можно перейти от картины Шредингера к картине Гейзенберга и описать временную эволюцию уже не матрицы плотности, а наблюдаемой A уравнением

A= - Y ( A - ct 3 Act 3) ,           (20)

решения которого

CT x (t ) = e ^-Yt CT x , CT y (t ) = e ^-Yt CT y , CT z (t ) = CT z , (21)

также можно представить преобразованиями Крауса

A ( t ) = Л A (0) =

= E +( t ) A (0) E o( t ) + E + t ) A (0) E z ( t ) , (22) где E i ( t ) совпадает с (12) при е = e ^—Yt .

Определяя новый коммутатор в алгебре наблюдаемых как

[ A i ,A j ] t = (Л) ^— 1[Л A i , Л A j ] ,        (23)

получаем новые коммутаторы для σ i

[ CT x , CT y ] t = 2 i e ^{— 2 Y}t CT z ,

[ CT y ,CT z ] t = 2 iCT x ,       [ CT z ,CT x ] t = 2 iCT y ,

дающие в пределе t ^ ж алгебру Евклида e (2)

^{[ CT} x ,^CT y ^] ^    ⁰ , ^{[ CT} y ,^CT z ^] ^    ^{2 iCT} x , ^{[ CT} z , ^CT x ^] ^    ^{2 iCT} y •

(25) Наблюдаемые σ _x и σ _y здесь коммутируют, что может интерпретироваться как переход от квантового поведения к классическому для этой пары. Оставшиеся две пары сохраняют характерные квантовые свойства.

• 2. 1. Канал с переворотом фазы с эволюцией по спирали

Рассмотрим канал с переворотом фазы с более сложной, чем (15), (16), рис. 3 траекторией перехода матрицы плотности к предельному выражению, записав уравнение Линдблада (2) с гамильтонианом [12]

H = 2 ~ wCT 3 ,               (26)

которое в этом случае принимает вид p = у[p,CT3] - 2 1p — CT3PCTз) , или для переменных x, y, z z = 0, x = —Yx — wy, y = — Yy + wx, с решением

( z = z 0 ,

< x = e ^-Yt ( x о cos wt — y о sin wt ) ,      (29)

( y = e ^-Yt ( y о cos wt + x о sin wt ) .

Соответствующая эволюция матрицы плотности определяется выражением p (t) = Л( t) p (0) =

= E 0( t ) p (0) E 0 ⁺ ( t ) + E Z ( t ) p (0) E z ⁺ ( t ) =

. 1 A 1 + z о         e ^-Yt-i^t ( x о — iy о) )

• - 2    e ^{-Yt +} i“t ( x о + iy о)          1 — z о         J ,

в котором операторы Крауса теперь имеют вид

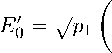
e 2

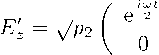
P 1 + P 2 = 1 , P 1 — P 2 = e ^Yt

Эту эволюцию можно интерпретировать как контракционное преобразование с е = e ^-Yt . Предел матрицы плотности при t → ∞ тот же (14), но с другой эволюционной траекторией, изображенной на рис. 4.

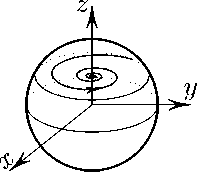
Рис. 4. Эволюция матрицы плотности (30) по спирали.

Fig. 4. Spiral evolution of the density matrix (30).

Динамика наблюдаемых определяется уравнением

iω        γ

A = — [ ct 3 ,A ] — 2 ( A — ct 3 Act 3)       (32)

с решением

A ( t ) = E ₍ ; +( t ) A (0) E о( t ) + E Z ⁺ ( t ) A (0) E z ( t ) , (33)

из которого для конкретных наблюдаемых σi получаем ctx (t) = eYt ^ e iLt сту (t) = e-Yt (i e0Lt e—iLt 0

,

CT z ( t ) = CT z ,

•

—i e

iωt

,

с коммутационными соотношениями (24).

• 2. 2. Система двух кубитов

Возникновение контракций матрицы плотности в открытой системе можно проследить без использования преобразований Крауса. Рассмотрим замкнутую систему, состоящую из двух кубитов, один из которых будем рассматривать как окружение (резервуар) другого кубита. Пусть в начальный момент времени система находится в состоянии ф = |0 )®| 0)-    р (0) = |ф><ф|-     (35)

а ее эволюция описывается уравнением

Р ( t) = U ( t) р (0) U + (t),             (36)

с унитарным оператором U ( t ) следующего вида

U ( t ) =

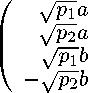
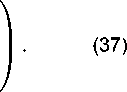
Здесь точки означают элементы матрицы, которые в данном случае не имеют значения и могут быть любыми, главное, чтобы матрица U ( t ) была унитарной. Числа a, b свяжем с координатами x, y, z вектора ⃗r формулами

Ы2 = 2 (1 + z), |О|2 + b2 = 1, ab* = 2 (x — iy).               (38)

Заметим, что состояние |ф ( t ) ) = U ( t ) |ф) при такой эволюции становится запутанным ф ( t ) ^ = vpi ( a )®i 0 > + vp2 (-a )®i i >. (39)

Тогда, взяв след по пространству второго кубита в матрице плотности р ( t ) = 1ф ( t ) )(ф ( t ) | , получим (18) для первого кубита.

Таким образом, появление контракционных множителей в матрице плотности открытых систем является универсальным свойством. Возможное при этом обнуление недиагональных элементов матрицы плотности связано с декогеренцией квантовых систем. Однако существуют отображения (4), при которых когерентность сохраняется, несмотря на обнуление некоторых коммутаторов. Примеры можно найти в работе [10].

• 3.    Канал с затуханием амплитуды

Рассмотрим теперь канал с затуханием амплитуды [3, 9], соответствующий афинному отображению (5) с е ₁ = е ₂ = е и с 3 = 1 — е ² . Преобразование Крауса в этом случае неунитально ( с 3 = 0 ) и имеет вид

Р = E о рE + + E i рE + =

= 1 / 2 + e -^Yt ( z — 1) e - ^Y ( x — iy )

2 \ e - Y r ( x + iy )    e -^Yt (1 — z )

где

, (40)

E1 = ( 1 eФ ) -E1 = V1 — e"Yt ( 0 0 )• а предельным состоянием при t → ∞ является р (TO) = 2(° о+ ° з) = ( 0 0 у

Уравнение Линдблада для H = 0, v = x -+, 2°± = ox ± i°y имеет вид р = — Y ({°-° + ,P} — 2°+р° ) • а соответствующая динамическая система γ x =--x,

2 ^-

γ

У = — 2 У- z = —y (z — 1)

имеет решение x = e- Y tx о, y = e- Y ty о, z = e-Yt (z о — 1) + 1.

Уравнение для наблюдаемых

^A = — 2 ^{( {}° - ° + • A^} — ² ° - Ao +)

приводит к зависимости от времени

A ( t ) = Л A (0) =

= E +( t ) A (0) E о( t ) + E +( t ) A (0) E i( t ) , (47)

которая для σ _i выражается формулами

° z ⁽ t ) = ^{e Y}t ⁽ ° 3 ⁺ I) ^— I •

° x ( t ) = e ^- Y t ° x ,     ° y ( t ) = e ^- Y r ° y .

Коммутационные соотношения при этом становятся равными

[ ° i • ° 2] t = ² i ( ° 3 ^{+ (1 — e Y}t )I) •

[ ° 2 -° 3] _t = 2 i e ^-Yt ° 1 ,      [ ° 3 -° 1] _t = 2 i e ^-Yt ° 2 .

Переобозначая ° 3 + I через ° 3 , в пределе t ^ ж получаем алгебру Галилея (или Гейзенберга) g (2)

^[ ° 1 ^-° 2^] ^ = ² i° 3 • ^[ ° 2 ^-° 3^] ^ = ⁰ •

[ ° 3 -° 1] ^ = 0 .                (50)

Физические примеры, приводящие к уравнениям Линблада для затухания амплитуды, разобраны в статье [15].

• 4.    Канал Кэли-Клейна

5. Трехпараметрический канал

Преобразования (8) принято называть в теории контракции алгебр so (3) или su (2) преобразованиями Кэли-Клейна. Сравнивая с (5), мы видим, что оно представляет собой общее неунитарное квантовое преобразование с с ₃ = 0 . Имеем матрицу плотности

р(t) = ^ Ek (t)р(0)E+(t) = k=0

-12 1 + е 1( t ) е 2( t ) z   е 1( t ) x + ie 2( t ) y\     (51)

2 у е 1(t)x — ie2(t)y 1 — е 1(t)е2(t)z J • 1 } с операторами Крауса

E 0 = Vp 0 ¹ ,

E y = VP 2 a y ,

E x E z

V P 1 a x ,

VP 3 ° z ,

где pi связаны с ei(t) следующим образом po(t) = 4 (1 + e 1(t) + e2(t) + e 1(t)e2(t)), p 1(t) = 4 (1 + e 1(t) — e2(t) — e 1(t)e2(t)), p2(t) = 4 (1 — e 1(t) + e2(t) — e 1(t)e2(t)) , p3(t) = 4 (1 — e 1(t) — e2(t) + e 1(t)e2(t)) • (53)

Преобразование контракции с помощью матрицы E = diag( e 1 , e ₂ , e ₃ ) определяет канал с матрицей плотности

P = E ( p ) = V ^{1 + e 3} z   ^{e 1} x ^{+ ie 2 y} \ (61)

2 e 1 x — ie 2 y    1 — e 3 z

Сфера Блоха при этом сжимается неравномерным образом. Соответствующие преобразования Крауса порождаются операторами

Уравнение Линдблада (2) для этого канала за- дается операторами H = 0, Vx = t/^ax, Vy =

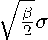
и имеет вид

α β

P = — 2( P — a x pa x ) — ^( p — a y pa y ) •    (54)

Динамика переменных x, y, z описывается уравнениями z =

X = ^y =

— ( a + в ) z,

-βx,

-αy,

с решениями z (t) = e (a+e) tzо, x (t) = e etxо,

У ( t ) = e ^-at y о •                 (56)

При e i( t ) = e ^-et , e ₂ ( t ) = e ^-at для p ( t ) получаем в точности выражение (51).

Уравнения для наблюдаемых в этом канале записываются в виде

αβ

A = — 2 (A — axAax) — 2 (A — ayAay) •

Зависимость от времени может быть представлена с помощью операторов Крауса

A (t ) = ^E^j t) AEk (t)

k =0

и для наблюдаемых σi выглядит так ax (t) = e "etax, ay (t) = e -atay, az (t) = e -(a+e) taz •(59)

Вычисляя коммутационные соотношения (23), получим

[ a 2 , a 3] t = 2 ie 2( t ) a 1 , [ a 3 ,a 1] t = 2 ie 1( t ) a 2 •

[ a 1 , a 2 ] _t = 2 ia 3 ,

В работе [13] в качестве условий сохранения когерентности двухкубитных состояний при квантовых преобразованиях было использовано соотношение вида e ₃ = —e 1 e ₂ , которое с точностью до знака выполняется и в канале Кэли-Клейна.

E 0 = Vp o 1 ’ E 1 = Vp i a x , E 2 = Vp 2 a y , E 3 = Vp 3 a z , P 0 = 4 (1 + e 1 + e 2 + e 3) , P 1 = 4 (1 + e 1 — e 2 — e 3) , P 2 = 4 (1 — e 1 + e 2 — e 3) , P 3 = 4 (1 — e 1 — e 2 + e 3) •

Отметим, что в задаче о распутывающем квантовом канале [14] тоже возникают подобные соотношения.

Уравнение Линдблада с HH = 0 , V _x = ^ ^ a x , V y = V ^ a y , V y = V 7 a z приводит к матрице плотности

αi у (p — aipai) •        (63)

i = x,y,z

Динамические уравнения для компонент вектора Блоха

( z = — ( a x + a y ) z,

< i = — (ay + az) x,(64)

I y) = — (ax + az )y имеют решения z (t) = e - (ax + ay) tz 0, x (t) = e - (ay+az) tx 0, y (t) = e - (ax+az) ty 0 •(65)

Связь параметров αi и εi задается формулами e 1 = e — (ay+az) t e 2 = e— (ax+az) t e 3 = e- (ax+ay)

Эволюция наблюдаемых описывается уравнениями

α

A = —22 21 (A — aiAai)

i=x,y,z с решениями вида ax (t) = e - (ay+az) tax, ay (t) = e - (ax+az) tay, az (t ) = e - (ax+ay) taz •(68)

При равенстве всех параметров e i = e в пределе e —> 0 получим абелеву алгебру, т.е. наблюдаемые кубита становятся классическими. Этот случай соответствует деполяризующему каналу.

Заключение

Контракционные преобразования исходной алгебры наблюдаемых кубита связаны с эволюцией его матрицы плотности при диссипации. Пусть структурные константы алгебры наблюдаемых (с точностью до вращений) изменяются во времени следующим образом

[ O x , O y ] t = a ( t ) O z ,   [ O y ,O z ] t = в ( t ) O x ,

[ O z ,O x ] t = Y ( t ) O y .                (69)

Контракция алгебры может быть схематично представлена траекторией ( a ( t ) ,e ( t ) ,Y ( t )) (см. рис. 5) В пространстве структурных констант [16], точки которой соответствуют изоморфным алгебрам. Предельная точка ( a (0) , в (0) , Y (0)) будет описывать контракцию исходной алгебры, соответствующую обнулению недиагональных элементов матрицы плотности. Путь к предельной точке, лежащей на плоскости a = 0 , описывает контракцию к алгебре Евклида e (2) , которая происходит в канале с переворотом фазы. Путь к предельной точке на оси α описывает контракцию к алгебре Галилея g , отвечающую каналу с затуханием амплитуды. Наконец, путь к нулевой точке O , т.е. контракция к абелевой алгебре, связан с деполяризующим каналом.

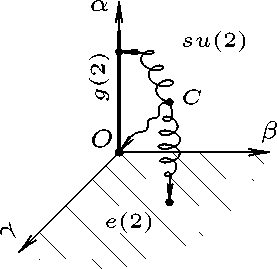
Рис. 5. Предельные переходы в пространстве структурных констант.

Fig. 5. Limit transitions in the space of structural constans.

С другой стороны, эволюция матрицы плотности кубита при диссипации и декогеренции приводит к контракции алгебры, при которой частично (или полностью) обнуляются коммутаторы наблюдаемых, что свидетельствует о частичной (или полной) потере кубитом квантовых свойств.

Работа выполнена при частичной финансовой поддержке Программы фундаментальных исследований УрО РАН, проект №18-1-1-7.