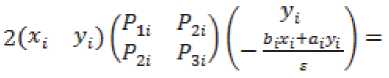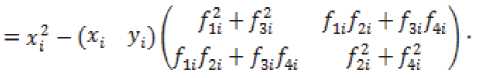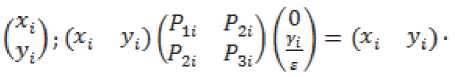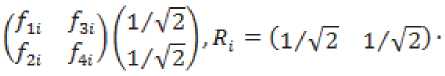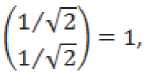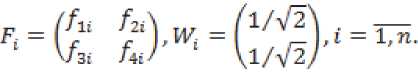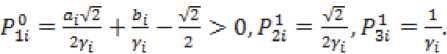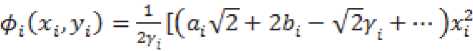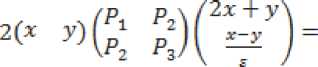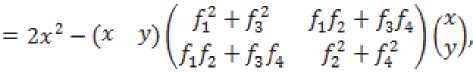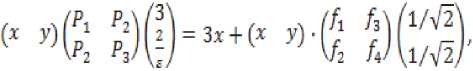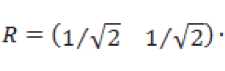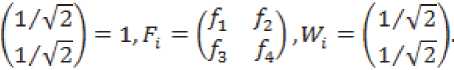Диссипативность линейных трехтемповых систем
Автор: Семенова М.М.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 2 т.24, 2022 года.
Бесплатный доступ
В статье излагается метод определения функции запаса. Исследуется диссипативность трехтемповых систем. Приведен пример, иллюстрирующий полученные результаты.
Линейная трехтемповая система, функция запаса, диссипативная система относительно функции расхода
Короткий адрес: https://sciup.org/148324482
IDR: 148324482 | УДК: 517.9 | DOI: 10.37313/1990-5378-2022-24-2-58-63
Текст научной статьи Диссипативность линейных трехтемповых систем
Исследованию свойств пассивных и диссипативных нелинейных систем посвящено большое количество публикаций. Это объясняется широким спектром приложений таких систем: гидродинамика, электроэнергетика, радиотехника, динамика полета и др. Общее понятие диссипативной системы введено в работах [1,2]. Понятие диссипативности по Виллемсу означает, что решения системы удовлетворяют интегральной связи с некоторым функционалом (функционалом расхода) от входа и выхода системы; им показано, что в этом случае на пространстве состояний системы можно определить функцию, которая при определенных условиях будет играть роль функции Ляпунова системы. Таким образом, понятие диссипативной системы позволило рассматривать устойчивость системы по Ляпунову и устойчивость в смысле конечности нормы вход-выходных отображений [3]. В работах [4,5] развиты методы теории диссипативных систем. В обзоре [6] рассматриваются некоторые результаты, касающиеся анализа и синтеза управления нелинейными системами на основе понятий пассивности и диссипативности. Условия пассивности в задаче стабилизации нелинейных систем с помощью обратной связи получены в работе [7].
Данная работа посвящена исследованию диссипативности линейных трехтемповых систем относительно функции расхода. Цель работы – найти функцию запаса линейной трехтемповой системы.
ДИССИПАТИВНЫЕ СИСТЕМЫ
Рассмотрим модель линейной трехтемповой системы вида:
Ш=о Ek^i ~ T^tqA^Xj + Btu,i — 0,2;
У ~ Sj=o ^jxj, (1)
где t E R,^ E R\u EF,y E RP^Bp CpiJ = 0^ - постоянные матрицы соответствующих размерностей, et, i = 1,2 – малые положительные параметры, so — lj и функция расхода iv(u,y) = y' Qy + 2y'Su + и Ru, где Q,S,R
– постоянные матрицы, причем Q, R – симме- трические, штрих означает транспонирование.
Определение 1. Вещественно-значимая функция w: ^o+n^nz у Rr X Rp -» R такая, что для любого t > 0, любого начального состояния x(0) = x° и любого допустимого управления uC-) выполняется Jo I^C^c^^^^^c^'yC5))!^5 ^ +°°' называется функцией расхода системы (1).
Определение 2. Система (1) называется диссипативной относительно функции расхода w, если существует функция V: K"o+”i+"z -> R+, у e c° такая, что для любых x(0) = x°, для любых допустимых управлений u(-) и для любого t > 0 выполняется неравенство ^(x1) < V(x°) + Jor w(x(s),u(s),y(s))ds, где x1 = Ф(х°Д, u). Функция V называется функцией запаса системы (1), а неравенство на- зывается неравенством диссипации.
Пусть для системы (1) выполняются предположения, аналогичные условиям Ai-A4, при-веденные в работе [6]:
Для любогоx(t0) = X и любого допустимого u(") существует единственное решение системы (1). Это решение определено на[^+®) и таково, что y(-) – локально-интегрируемая с квадратом функция.
Система (1) глобально достижима из начала координат. Это означает, что для любых .\" Е 7/'г-' -_'': : существуют :■ 1 : и такие, что <Ф(х(О), tx — tc/u) = х1.
Введем функцию доступного запаса у, >•. ■ = - :-Л _.:. । ;,■ ;„ v ■■- которая предполагается дифференцируемой по х.
Функция расхода ;■/ удовлетворяет условию: для любого / = 2 найдется ^ такое, что w<^ < 0. --
Собственные значения ■. : = _ -. матрицы л-- удовлетворяют неравенству Re /Ц(Л22) < -2/? < 0.
Для построения функции запаса S’ х ■ = л Рл :■■ = Л -V_ х- ■ запишем необходимые и достаточные условия диссипа-тивности [8] системы (1) относительно функции расхода ;■/:
Эф V2 л I ®Ф V*2 л v Эф
ЗД^^о^оА+^^Е.^!^ +^
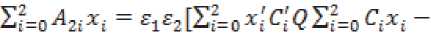
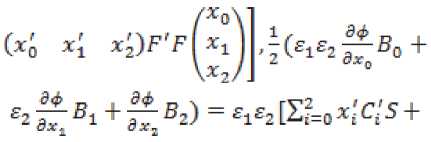
(%о %; x2)F'IV],/? = W W
При j = 5- = 2 получим систему
— У2 А х
ЭХ1^=° 2j j
= 0,^~В. = 0, R = И/'ИЛ
2 Эх2 z
Матрицу Р будем
искать в
виде
(РР
*11У
£1^12
£1^2^ 13 £1^2^ 23
£1£2^1з\ где
£1£2^33/
Р = р°-о.£ р^ + е род + £ £ Р1Д А, Егр2.о Mj Т E^j Т Е2Гу ЕгЕ2Гц т ЕгГ-.
2 0,2, ,
“у^ ■ “ 1 :_ = -- 2. Полагая, что матрица '. 1-' квадратнаяневырожденнаяматрица, извторо-го уравнения, получим г = 75 - С 5'/--пусть Р = ’V-" и подставив в первое уравнение, получим уравнение Лурье РН + Н 'Р - PLP + М = О, Н = (^ X hy = ^^T^i . L = h\
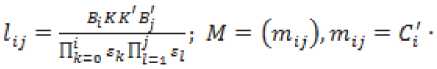
(Q - SKK'S'^Cpij = 0,2.
Уравнение Лурье имеет единственное положительно определенное решение. Обозначим, ^о,о_ ^^^^/^^^^, j^i'O _ К^*^ ^К^^У | К^*^
(КаоуТм = К°'°(К0Д)' + к0-1^0-0)', т1Д = ка'а(к1Ду + /c1't>(№’1)' + кал ■
(К 1,0)/ + к 1,1 ^0,0) !Т 2,0 _ /(-0,0 ^2,0)/ + ду^'0 ^2^^“^^/ | К^*^ ^К^'^у ^ о,2 _ К^'^ ■ (tfO-2)' +/f 0,1(^0,ly +/f 0,2^0^^ ...
Выполняя действия и приравнивая соответствующие элементы матриц, получим систему 6 линейно независимых уравнений. Система нулевого приближения имеет вид:
5=1['’1^(^-и-в,,1г">.
5=, в;,^^)')]+Е^^ЛЧ^Л +C,0(y-5T°'°S,)Ck = 0,к = 03,Z = 13; 5=г[₽“((л°-1.») - в,-1Тм д=, в;_, • (р”0)')1+ е^.^ч)'^,?0)' +с; w - 5pO,os/)Ck = о, к = 1,2, Z = 2,3;
^°« - В2Т^В’2Р^ + (^“2)'^ + CAQ - STq'qS')C2 = 0, Л°- = B.T^S'Ci -^ ■'Ле Ч * У
А i,j = 0,1,2
Последнее уравнение этой системы - уравнение Лурье, положительно определенное решение которого существует и единственно [9], „о,о _ .0,0 _ , г-- — _ -.. Подставим это решение в третье и пятое уравнения системы, которые примут вид:
ро,од1 а. р0'°д! 4- рО'Од1 4-ГД° У 70,0 Л1 02 ■ Лг Н12 ■ yis н22 ■ 1^207 ьзз
+ОД - ST°'°S')C2 = О, Р^А^ + р^1 ■ л^2 + №)'4° + с; ( - sr0-^ эс2 = О, где .< = Л1, - 5 "::5:i" : = 2 1 2. Из п 0/0 f «f х « пятого уравнения, получим ^-. = _ з
T«“S'-Q)C2 - M’J'L"’ - р“л*2) • (лу-1.
Подставив Рл" в четвертое уравнение, получим уравнение Лурье:
р. . ^- P.V - Р. . :БР. . : - с = 2 где
^ Д Д Д Д Д ill ill д=4 - л^гх - я^а^ггч^ ■ T°-°S' - Q3CT - 4^^) - АХМ2УгВ2 ■ т°-°в'2 ((A^T^ST^S1 - oq - 4^), в = в.то,ов'.-аКСа^У1 в2 • тмв[ - B -(С;(5Гвд5'-0Х2-(^1)'-Ь^УА^В^В'^А^ТЧСг^ -У)^-/,0^) + C^Q-ST^S'y,. Это уравнение имеет единственное поло- „0,0 ,0,0 жительно определенное решение ^ 22 * „0,0 _ .0,0 _ .o,of.o,o .о,ох ТТпп- Значит, Под ставим найденные решения во второе и третье уравнения. Из третьего уравнения найдем Р» = (Cj(STMS- - Q)C2 - (л"0)'^ - р^л^ - Р^Хлу1. Подставим во второе уравнение, получим Р^1+Р™А^П(^ Ли = A-Л^СД^) ^°i + (4(4) 1" О 70,° _ e ro.o^y^ao + 5vLMy> £ = оД °^- L3°) = (^(ST^S' - 0c2 - ЮШ^Й " B^CB^ + 5;K°)')+Mo)'^+ИЖУ - cite - ””$% этого K^)1, уравнение, уравнение Выразим из рм = (-D -Р^А1 42 V и 41 н01 ставим в первое зультате получим уравнения и под-в ре Лурье: р°-°д1 + (А1 УР0,0 - pQ'QBOlOP0,0 + Ноя = 0 Л1 гц н00 ' V^OO? ГЦ rH D гн т п и^00 ^00 ^01 ^-И 7 W10 ' ^12 <-^227 Л^У-Л^С^)"^ * VBqT^b; ■ ((Л^)')"1 - А^А^УЧВ^В; + Л}2 -(Л212)-1327’0-03[((дЬ)')-1)-Л^2(Л^2)-1 ■ B^BKC^T1]" [4(ST°-0S' - Q)C0 "(№)' + ЙА + ^В^Т^В^ ■ ((А^УУЧС^5ТМ5' - Q}C0 - 4'3°Л%) —L°'°A0 — L°'°A0 1 — ь22ЛЮь 23 *401 Ld0 -^UU1 - (в1 + л^Сл^Г^-л^н)"1^]?'0'0 • B^^DD’^^CST^S' - Q)Co - 4°Л20 ^УЮГ1»^ - № - Ю+(4^+ВДт1^ ■ №^s' - №. - 44) - 44 - W (Ar1^ - л^л^ват00^ - в; -((лиэ-Чл^'+УЧС^Э-Чл^У), 0,0 – д2 = j1 — (д1 V1 л1Н ^02 ^02 ^01 V^llJ л12'п все сла- р0,0 хпзппиогттло гаемые, не содержащие 41 ■ Это уравнение имеет единственное положительно определенное решение 41 — ^и' из которого получаем „0,0 ,0,0 ,0,0 ,0,0х,0,0 ,0,0 ,0,0^ . —- Plj = Ч) ' Ч) = Llj (^1V L22' L33^a = 2,3. Приравнивая коэффициенты при первых степенях малых параметров £1 и s2, получим систему линейных уравнений: уз р'1Л2 .1(к+1) I уз /д1(2) у A-j=2r2j ^j-l* A,j=k+l\Hj-l.l) ( Plv4 V = уА'^ t = 1 2- P11'11 Д1(3) k^k+L// V2,k+VK X'2*1 *33 H22 411(34 Plvla = yzvz2 1 4. / =17 ф I ^22 J гзз *зз 'Чт^г ^ti^taj Z, e {0,1}, i = 1,2, где Л,0 ^ — ^to BiT0,0 • (вД + в;И“)' + в;(1“)'),л^я = : А^-В.Т-ЧвЯ + B^L“)'),A^ = А^ ■ В^^В^Л = 0^;^ – постоянные матрицы. Из двух последних уравнений этой системы, получаем D1^ _ Г^О -0,1 _ .0,1 „ *33 L33* *33 — ^33" Потребуем, чтобы матрицы L и ^aa были положительно определены. Из девятого и десятого уравнения выразим н 23 \ 23 22 12 ) Гд113^1v1^1* =vk'la-(a1W\ ^**22 / ' ’23 ’23 \ 21 / 33 ' k13 43 ^20 / b33 +Z2 = 1, lT Ф 12,Ц E {0,1}, i = 1,2. Подста вим эти выражения в седьмое и восьмое уравне- ния системы, получим: nii.Z2.l(4) / !(4)y v, = гд,,.1(4) 42 11 ' \11 У 42 v22 = Д1(2) - Д1(3)Гд1(34 41(2) = уггг2 _ Л11 **12 V^ZZ / ' *22*22 yV- - (A^a)'^А^А^» + + №)' (№’)') 1(te,‘)' - ^ ■ A^yit + 4 = 1,4 * ЧЦ e {0,1},i = 1, 2. Эти линейные уравнения с невырожденной матрицей имеют единственное решение = гУ P*1 = r^1 ^22 L22^ ^22 ^22’ Потребуем, чтобы эти матрицы были положительно определены. Под- ставим найденные решения в третье и четвер- тое уравнения, получим линейные уравнения: рк-Чд1^) I рк-Чд^ = vlv4* .1(4) = 41 01 ' 1Z 11 12 ?л01 Ц2) _ 1(3)7 1(3) \ 1 1(2) lvla* = lvl2 01 02 \"22 У л22 ' ’12 ’12 Отсюда, Подставим найденные решения в первое и второе уравнения, получим два линейных уравнения рЧ'Ч дА 41 оо РЧ-Ч= тАЧ* д1^ = 41 41 'оо А = л1(1)-л1С4Ул1(4)>1Л00 Л01 \Л11 / Ж’Г^М "\^ 1(1) п Отсюда, piTiz _ LV» / + г = 1 J * L, L е {ОД}, I = 1,2, ДД ДД X X X X I ^1 = Ур£У1 = -а1У1 - bi4 + Yiu-Zi =Xi,i = 1,П. Функция расхода для -ой подсистемы Пусть для систе-мывыполняютсяусловия 1–5. Функциюзапасабу-демискатьввидеФ^.уО = (xt УдРД^У xj i/ (Pa: PliX ___ Запишем необходи- V.£2i - мые и достаточные условия диссипативности -ой подсистемы относительно функции расхода и т. д. Приравнивая коэффициенты при получим следующую систему линейных уравнений уз рЧ-Ч д1(т+1) . уз f Д1^ V- A-llj j-l,m ^j = m+l\Hj-V0j Из по следних уравнений находим __ г к,о Dk-1^1 ,к—1,1 n 0,к у 0.1 к Rr тгтпп Выполняя те же действия, что и для «первого» приближения, найдем все остальные неизвестные последней системы, при этом требуем, чтобы все блоки, стоящие на главной диагонали матрицы были положительно определены. Таким образом, элементы матрицы могут быть найдены как асимптотические разложения по малым паР Р ■ Р == раметрам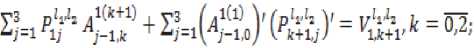
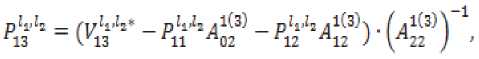
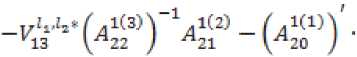
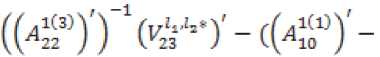
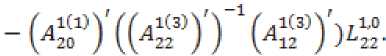
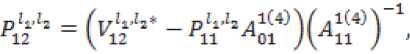
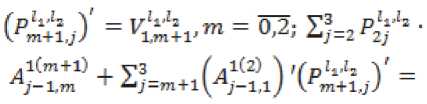
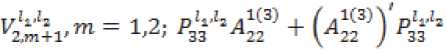
Список литературы Диссипативность линейных трехтемповых систем
- Willems J.C. Dissipative dynamical systems. Part I: General theory // Arch. Rational Mechanics and Analysis. 1972. V. 45. P. 321-351.
- Willems J.C. Dissipative dynamical systems. Part II: Linear systems with quadratic supply rates // Arch. Rational Mechanics and Analysis. 1972. V. 45. P. 352-393.
- Desoer C.A., Vidyasagar M. Feedback systems: input-output properties. New York: Academic, 1975. 264 p.
- HillD., Moylan P. The stability of nonlinear dissipative systems // IEEE Transactions on Automatic Control. 1976. V. 21. P. 708-711.
- Hill D., Moylan P. Dissipative dynamical systems: Basic input-output and state properties // J. Franklin Inst. 1980. V. 309. P. 327-357.
- Полушин И.Г. Пассивность и пассификация нелинейных систем / И.Г. Полушин, А.Л. Фрадков, Д. Д. Хилл // Автоматика и телемеханика. - 2000. - № 3. - С. 3-37.
- Byrnes C.I., Isidory A., Willems J.C. Passivity, feedback equivalence, and the global stabilization of minimum phase nonlinear systems // IEEE Transactions on Automatic Control. 1991. V. 36. № 11. P. 1228-1240.
- Семенова М.М. Алгебраический критерий дисси-пативности сингулярно возмущенных систем / М.М. Семенова // Обозрение прикладной и промышленной математики. - 2001. Т.8. - Вып. 1. -С. 408 -409.
- Андерсон Б. Устойчивость адаптивных систем: пер. с англ. / Андерсон Б., Битмид Р., Джонсон К. - М.: Мир. - 1989. - 263 с.