Диссипативность многотемповых систем

Теория сингулярно возмущенных систем дифференциальных уравнений интенсивно развивается и методы ее активно применяются для решения задач из различных областей естествознания и техники. Это объясняется широким спектром приложений таких систем: гидродинамика, электроэнергетика, радиотехника, динамика полета и др. Сингулярно возмущенные системы могут быть получены естественным путем не только при моделировании, но и при исследовании объектов, которые совершают одновременно медленные и быстрые движения. Движение систем твердых тел представляет собой сложную композицию быстрых и медленных движений.

Данная работа посвящена исследованию диссипативности многотемповых систем относительно функции расхода. Цель работы – найти функцию запаса линейной многотемповой системы.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим модель линейной многотемповой системы вида:

Пк=о £_k*i = ^=о^АцХ, + B_tu,i = 0~n;

У = 2^=o Cj^xj.                         (1)

Определение 1. Вещественно-значимая функция W: ]RM»i+-+nn X R^r X R^p ^ К такая, что для любого t > 0, любого начального состояния x(0) = x и любого допустимого управления uf-) выполняется j^|w^(x°,s,u),u(s),y(s))|ds < +oo, называется функцией расхода системы (1).

Определение 2. Система (1) называет- ся диссипативной относительно   функ ции расхода w, если существует функция V: ^a+^+ '+nn ^ R+ у e CO такая, что для любых x(0) = x°, для любых допустимых управлений u(-) и для любого t > 0 выполняется неравенство ^(x1) < y(x°) + £ w(x(s),u(s),y(s))ds, где x1 = Ф(х°Л,г1). Функция V называется функцией запаса системы (1), а неравенство на- зывается неравенством диссипации.

Пусть для системы (1) выполняются предположения, аналогичные условиям Ai-A₄, при-веденные в работе [1]:

Для любого ^(t0) = x° и любого допустимого u(") существует единственное решение системы (1). Это решение определено на[^+®) и таково, что y(-) – локально-интегрируемая с квадратом функция.

Система (1) глобально достижима из на- чала координат. Это означает, что для любых x1 e Rno+ni+ ■+nn,t1 существуют ^ ^ t± и такие, что Ф(х(0)Л1 — ^O'u) = x1.

Введем функцию доступного запаса

4z(x₀) = - mfu,r>o Jq w(u,y)dt, которая предполагается дифференцируемой по .x«

Функция расхода w удовлетворяет условию: для любого у Ф 0 найдется it такое, что w(u,y) < 0.                     ___

Собственные значения Л,,1 = l,n матрицы A^ удовлетворяют неравенству пеХ^д^^-гр^^.

ПАССИВНОСТЬ ЛИНЕЙНЫХ СИСТЕМ

Для построения функции запаса л = л Рл л = v- :v_ ,, .\\. ■ запишем необходимые и достаточные условия диссипа-тивности [2] системы (1) относительно функции расхода -v:

yn-lprn ^ум л . ^

^4=0 Hk=Z+l ^bk _a_,^--j=O^Hlj^Aj ' а_

L*-*     *         *   *     V -А ^

X T^=0AnjXj = Пк=о£к [d^o^'i C*i)Q х (Z^ CjXj) - x'F'FxY

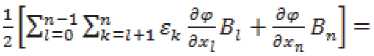
Щ=1 гкИко^С'^+х'Г'Н!

R = W'W.

При -- = 5- = ■=_-...= 2 получим систему

^_ У" А г = О - ■ ^Эф В = О

3x_n^Li=° "j i ^U,2 3x_n" ^U'

R = И^ИЛ

. no,o,...,l .                    , , . ^ —7

+^En^Pij + ^Е1^ЕЛ]    + -, I,; = 1, n +1.

Полагая, что матрица И-' - квадратная невырожденная матрица, из второго уравнения, получим г = ^5 - С J'/^-- обозначим --.=■ '.' - и подставив F и : V в первое уравнение, получим уравнение Лурье

PH А-Н'Р -PLP А-М = О,

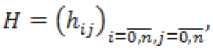
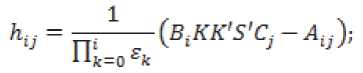
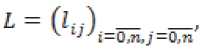
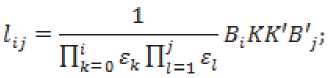
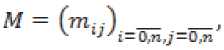
m^ = C^Q-SKK'S'^Cj.

Обозначим,

T = KK* T = 7 °’⁰'"’⁰ + e₁T^l0’™° ,

A-^T®-1.....0

, T0,0,...,l

1^2..."

Выполняя действия и приравнивая соответствующие блоки матриц, стоящих в левой и правой частях этого уравнения, получим подси стему с -   — -■; - "_ линейно независимыми

2       2

уравнениями.

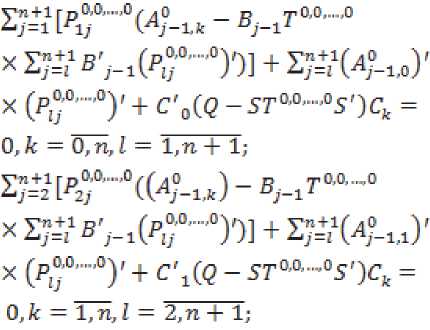
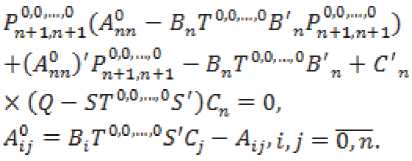
Последнее уравнение этой системы - уравнение Лурье, положительно опре- деленное решение которого существует и n OiOj.i.iO __ eOiOi.i.iO       р-r единственно [3],                         Под ставляя эти решения в остальные уравнения, находим положительно определенные решения соответствующих уравнений Лурье п о*о»*-»о   ж 0,0,...,0 ,  

7      - -      . - _ .. Отсюда получаем, п О,О,...,О _ , 0,0,...,0 . _ -5--- . _ ч-----ГТ ■ -L •

^Pij    ⁼ ^ij    ^{,l =} ^"-V ^{= 2,П} + ^lj^ ^ ^ll

Следующая подсистема состоит из :" - 3 ’1 - 2 ■ линейных уравнений:

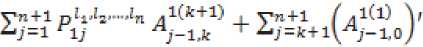
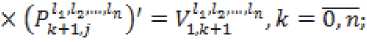
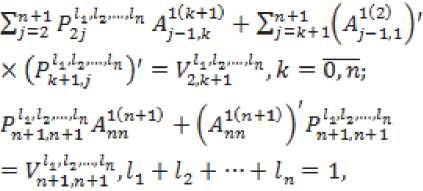
. ^ \ 2 2 . где матрицы-коэффициенты

ATti = Ail-BlTM-sK"«B,l-i

/'.О.О.-.-ОV «10+1) «О _ D р0,0,...,0 ^Х V^Lj+l,l )

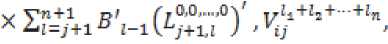
- постоянные матрицы. Все урав- нения этой подсистемы являются линейными. Требуем, чтобы их решения

„1,0,.„О _ .1,0,.„О „0,0,...,1 _ .0,0,..,!

i,j = l,n + 1 были положительно опреде- ленными матрицами.

.H. -ая      подсистема состоит из

(^n2+|n+l)(k+1)линейных уравнений

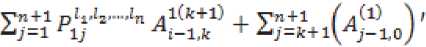
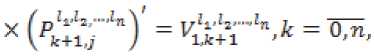
где индексы lm>o,l„ez,^1l„ = k, матрицы         – постоянные матрицы. Из этой системы однозначно определяются положительно определенные матрицы-решения ■ Элементы положительно определенной матрицы P могут быть найдены как асимптотические разложения по малым параметрам EV E^ ,^ Л * Условием положительной определенности матрицы j3 является положительная определенность ее главных блоков, т.е. блоков LlY4.....Si = l,n+ 1, следовательно, функция запаса

 OJi e Щ=1 Ц=к+1.

Пример. Рассмотрим систему, описываемую уравнениями: x = x + у + iz, ey = —у + и, z = x + у.

Эта система диссипативна относительно функции расхода w = x² + у² с функцией запаса

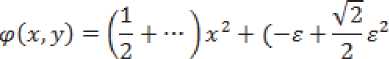
+ — )xy + ((1 + V2)e H-- 7~^£2

+ -)y2-

ЗАКЛЮЧЕНИЕ

Проведено исследование диссипативности многотемповых систем относительно функции расхода. Найдена функция запаса линейной многотемповой системы. Приведен пример, иллюстрирующий полученные результаты.