Диссипативные коэффициенты переноса кластеризующегося газа

При исследовании физических свойств сверхзвукового потока в рабочей части сверхзвуковой аэродинамической трубы [1] было обнаружено, что измеренные значения показателя преломления потока воздуха значительно отличаются от теоретически рассчитанных значений. Дальнейшее исследование свойств потока обнаружило источник расхождений — наличие в потоке гомогенных и гетерогенных кластеров молекул воды, кислорода и азота. Присутствие в потоке кластеров, обладающих кратной мономерам газа массой и повышенной теплоёмкостью, обусловленной наличием большого числа внутренних степеней свободы, с неизбежностью должно оказать влияние на диссипативные коэффициенты переноса кластеризующегося газа — его вязкость и теплопроводность. В настоящей работе исследуется влияние простейших кластеров — димеров воды на вязкость и теплопроводность водяного пара при умеренных давлениях (1-25 бар) и температурах (400-1100 К) в рамках квазихимической кластерной модели (КХКМ) газа [2].

• I.    Уравнение состояния газа в рамках квазихимической кластерной модели

Статистическая сумма газа Z , состоящего из совокупности мономеров и кластеров разного размера, рассматриваемых в данной работе как идеальный газ [2], позволяет найти статистический аналог свободной энергии Гельмгольца F , что даёт возможность записать уравнение состоя- ния газа в виде р=- (г),=-т (^),  ■"

Это уравнение оказывается уравнением состояния для смеси идеальных газов и подчиняется закону Дальтона — давление в газе равно сумме парциальных давлений мономеров и кластеров, распределение мольных долей которых вычисляется с использованием квазиравновесной функции распределения кластеров по размерам (по числу мономеров в кластере).

В простейшем случае, когда газ можно представить совокупностью только мономеров и димеров, уравнение состояния (1) записывается в виде p = pR о( fI + f2) T,          (2)

где f 1 = c 1 /ц 1 и f 2 = c 2 / (2 ц 1 ) — мольномассовые доли мономеров и димеров газа соответственно, c ₁ и c ₂ — массовые доли мономеров и димеров соответственно, μ ₁ — молярная масса мономера. Учитывая закон сохранения массы, зная значение плотности по модели идеального газа, состоящего только из мономеров ρ i , и измеренное в эксперименте значение плотности газа ρ _e , из уравнения (2) легко получить предельно возможное значение массовой доли димера в газе:

c 2 =2(1 - P i /P e ) .           (3)

Выражение (3) позволяет оценить массовую долю димеров в газе, не прибегая к сложным квантово-статистическим расчётам, если имеются в наличии экспериментальные значения плотности газа при заданных давлении и температуре, полученные с высокой степенью точности.

• II.    Коэффициент динамической вязкости паров воды в рамках квазихимической кластерной модели

В КХКМ газ представлен в виде смеси мономеров, димеров, тримеров и т. д. с числовой плотностью Ni,i = 1, 2, 3... На основании квантово-химических расчётов найдены мольные доли кластеров и диссипативные коэффициенты однокомпонентного газа в виде диссипативных коэффи- циентов для идеальной смеси кластеров. При этом использовались формулы для расчётов коэффициентов вязкости, теплопроводности как мономеров, так и кластеров, полученные в рамках классической теории Энскога–Чепмена по первому при- ближению [3]. При вычислении коэффициента динамической вязкости мономеров использовалась интерполяционная формула для расчёта вязкости пара воды в приближении идеального газа, рекомендованная в справочнике [4]. Коэффициент динамической вязкости димеров рассчитывался по классической формуле твёрдых сфер с диаметром газокинетического сечения ст = 4,963 • 10~10 м, полученным на основе квантово-химического расчёта структуры димера воды. В этом случае приведённый интеграл столкновения равен единице. Суммарный коэффициент вязкости для смеси вычислялся на основании формулы Уилки [5].

На рис. 1 приведены расчёты коэффициента динамической вязкости паров воды в зависимости от температуры при давлении 25 бар. В данном расчёте пары воды рассматривались в виде смеси мономеров и димеров воды. Кривая 1 (пунктир) — расчёт вязкости мономеров воды; кривая 2 — расчёт вязкости димеров воды; кривая 3 — расчёт вязкости паров воды по КХКМ;

— экспериментальные данные [4].

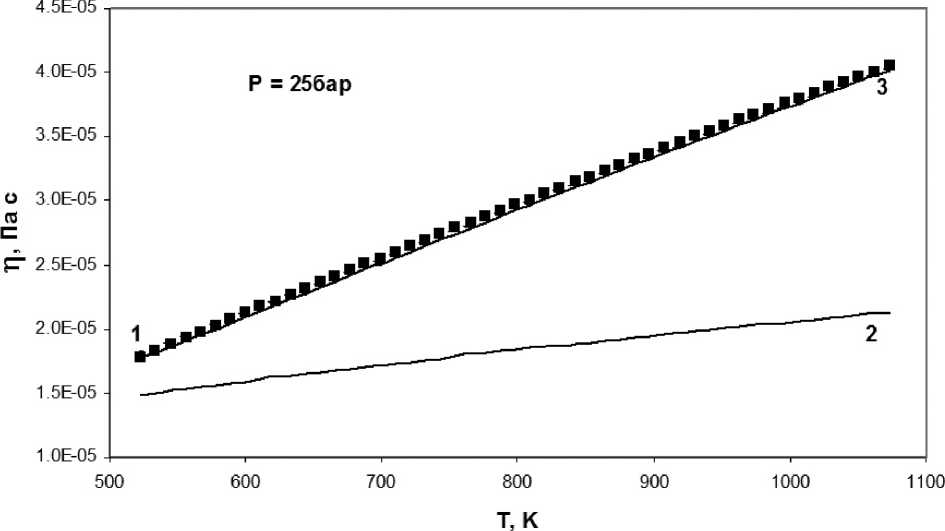
Рис. 1. Зависимость коэффициента динамической вязкости паров воды от температуры при давлении 25 бар

• III.    Коэффициент теплопроводности паров воды в рамках квазихимической кластерной модели

На рис. 2 приведены расчёты коэффициента теплопроводности паров воды в зависимости от температуры при давлении 25 бар. В данном расчёте пары воды рассматривались в виде смеси мономеров и димеров воды. Кривая 1 (пунктир) — рас- чёт коэффициента теплопроводности мономеров воды; кривая 2 — расчёт коэффициента теплопроводности димеров воды;

кривая 3 — расчёт коэффициента теплопроводности паров воды по КХКМ; — экспериментальные данные [4].

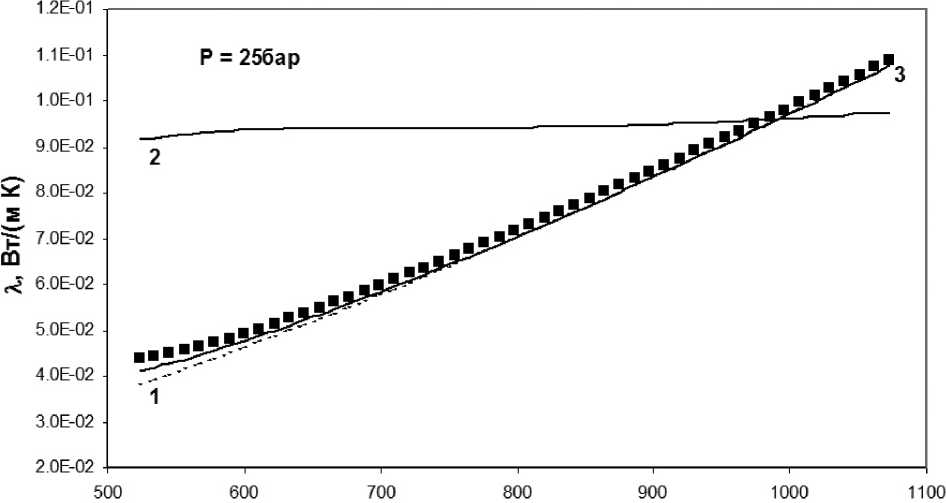
т, к

Рис. 2. Зависимость коэффициента теплопроводности паров воды от температуры при давлении 25 бар

При вычислении коэффициента теплопроводности мономеров паров воды использовалась интерполяционная формула для расчёта коэффициента теплопроводности пара воды в приближении идеального газа, рекомендованная в справочнике [4]. Коэффициент теплопроводности газа, состоящего из димеров воды, рассчитывался по классической формуле твёрдых сфер с диаметром газокинетического сечения а = 4 , 963 • 10 ~ ¹⁰ м. Удельная теплоёмкость при постоянном объёме димеров воды рассчитывалась в приближении ангармонического осциллятора с конечным числом уровней. Суммарный коэффициент теплопроводности для смеси (мономеров и димеров, концентрация димеров рассчитывалась по упрощённой формуле) вычислялся на основании формулы Мей-сона–Саксены [5].

• IV.    Теплоёмкость газа в рамках квазихимической кластерной модели

На основании полученных ранее выражений для статистических сумм кластеров можно, используя их связь с термодинамическими функциями, получить зависимо- сти теплоёмкостей кластеров произвольного размера:

' Г- 4 ( т 2 ( ^nZ n V)

Отметим, что колебательная теплоёмкость при постоянном объёме слабосвязанного кластера для модели в ангармоническом приближении или в гармоническом, но с учётом конечного числа колебательных уровней, может превосходить для колебательных мод димера его классический предел. Этот очень важный факт обсуждался в работе [2]. Другой особенностью ангармонических осцилляторов с конечным числом колебательных уровней является стремление колебательной теплоёмкости димера к нулю с ростом температуры.

На рис. 3 приведены зависимости теплоёмкости при постоянном давлении паров воды от температуры при давлениях P =1, 10, 25 бар. Расчёты проведены в рамках КХКМ с использованием нормальных частот и энергии диссоциации димера, найденных в [2], в предположении, что пар можно описать смесью мономеров и димеров, концентрация которых рассчитывается по упрощённой формуле (3).

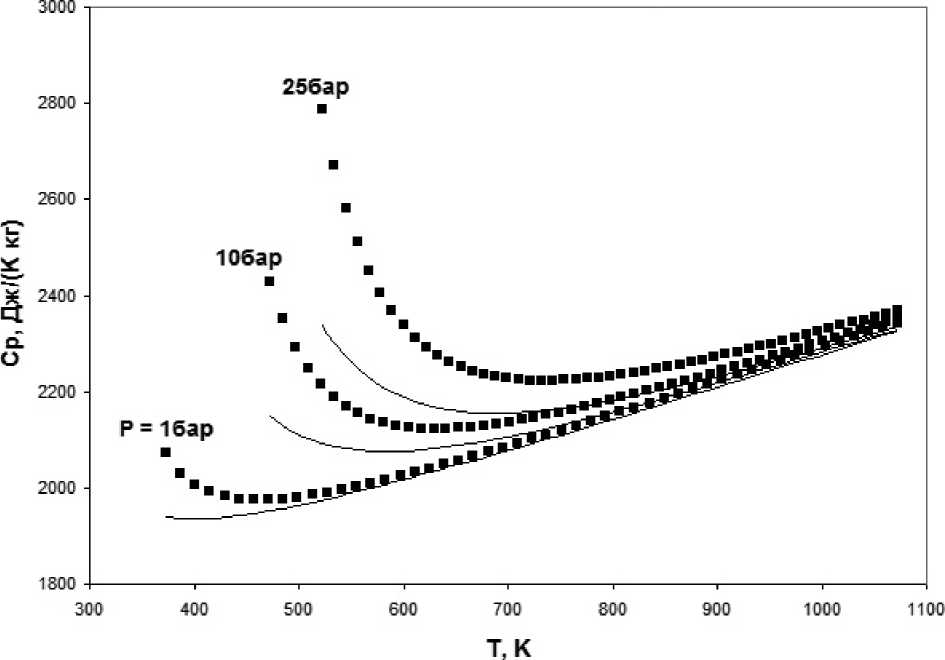
Рис. 3. Зависимость C P паров воды от температуры для давлений P =1 ,10, 25 бар

• V.    Выводы

Видно, что при низких температурах расхождение между расчётными и экспериментальными значениями теплоёмкости паров воды значительное, здесь необходимо принимать во внимание кластеры более высоких размеров с учётом функции распределения кластеров по размерам. Тем не менее даже в условиях такой упрощённой модели пара (идеальная смесь мономеров и димеров) в условиях самого высокого (из рассмотренного диапазона) давления 25 бар наблюдается неплохое соответствие рассчитанных и экспериментальных значений диссипативных коэффициентов вязкости и теплопроводности (рис. 1, 2). Таким образом, представленная упрощённая методика расчёта диссипативных коэффициентов реального газа в рамках КХКМ оказывается полезной и заслуживающей дальнейшего развития.