Distributed self-configuring evolutionary algorithms for artificial neural networks design

Self-configuring genetic algorithm. Genetic algorithm (GA) is an optimization method based on genetics and natural selection concepts [1; 2]. The use of GA in a problem solving is accompanied by the problem of relevant algorithm configuration selection.

In every task solving process there is certain optimal configuration (in terms of time consumption, number of calculations, number of fitness function calculation and etc.), which might be altered in process of algorithm functioning. Therefore, our task is to find such configuration to improve the program efficiency.

Flowchart of the self-configuring GA is presented in fig. 1. Presented scheme’s difference from standart one [3] is self-configuration section. It allows perform an adjustment of a given configuration in the process of the algorithm execution.

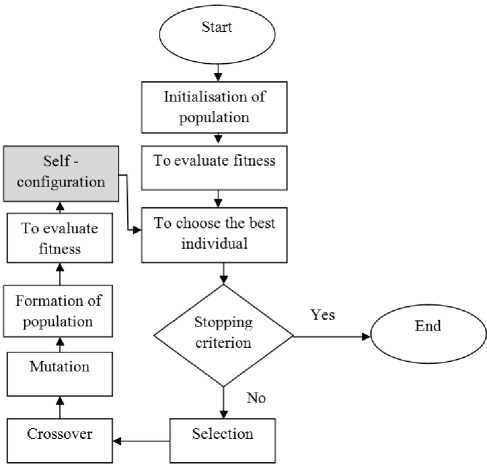
Fig. 1. Flowchart of self-configuring GA

Let us describe proposed adjustment approach. There are 3 groups of GA operators: selection, crossover, mutation. Each group represents a set of the following operators (table 1).

Table 1

Groups of the genetic operators

Selection	Crossover	Mutation
• Proportionate • Ranking • Tournament	• One-point • Two-point • Uniform	• Weak • Average • Strong

Operators shall compete for application in following algorithm iterations.

Let’s call as progressive chromosome the chromosome which fitness value surpasses current population’s average [4]. It’s necessary to make following statement: the number of the progressive chromosome resulted by the use of selection operator is equal to the sum of progressive chromosome resulted from crossover and mutation processes. Probability of operator being chosen is calculated as in following formula:

q

Pi =      , i ∑q jj

where q i is the number of progressive chromosomes, resulted from i -th operator. On the each algorithm iteration only one operator from each group is used. Therefore, it is crucial to accumulate certain number of iterations to enable further adjustment of operator selection probabilities.

Proposed approach allows adjusting several algorithms’ parameters: type of selection/crossover/mutation. However, selection problem of the numerical parameters (such as tournament size) still exists.

Given algorithm has been realized in form of computer program and tested on optimization tasks. Main efficiency criteria of EA is reliability, as it evaluates solution finding probability of given task. The algorithm reliability is a percentage of successful runs when the problem solution is found with required precision.

Since GA is a stochastic algorithm, it’s essential to evaluate efficiency by means of several runs. In our case, 100 unaltered program runs have been made for all algorithms. In figure 2, the reliability of conventional GAs with 90 different settings are compared with selfconfiguring GA on one test problem.

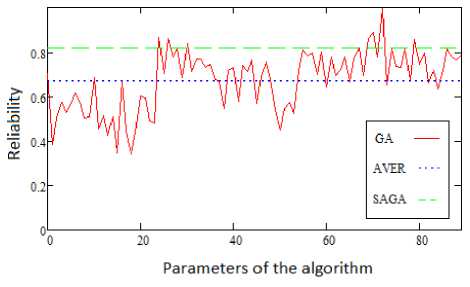
Fig. 2. GA reliability

The figure shows that the modification proposed (selfadjustment – SAGA) surpasses average GAs reliability value (AVER) and not much inferior to the reliability of GAs with the best parameters which resulted from the exhaustive search of settings.

Genetic algorithm in artificial neural network design. In this paper the following encoding method of artificial neural network (ANN) design in GA is presented. Certain number of hidden layers and the maximal number of neurons are given. Number of neurons on each of the layers is encoded in chromosome and adjusted by the methods of GA. Moreover, in each neuron’s chromosome specified number (type) of activation function is encoded. Resulting neural network is a perceptron with various activation functions.

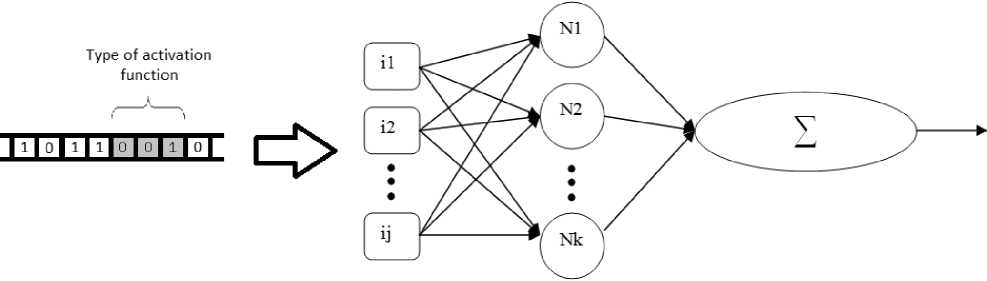
Fig. 3. An example of ANN

In this figure an example of simple ANN encoding by means of binary string is given. In this figure, Nk stands for k -th neuron (which is selected from the list of activation function) and ij – j-th input data variable.Presented algorithm has been realized in the form program system (ANN_GA).It’s effectiveness and comparison with existing algorithms is presented below. Learning procedure is based on the algorithm presented above.

Self-configuring genetic programming algorithm. Generally, functioning of genetic programming algorithm (GPA) is close to the one of genetic algorithm [5]. The most striking difference is in the encoding procedure. Whilst in GA individual is presented as a binary string of a pre-determined length, GPA uses trees.

The proposed above configuration selection schema has been applied to GPA. Moreover, a modification of the uniform crossover operator [6] is presented in the algorithm. When specified node transportation probability is given only one offspring is created, node sub-trees with different number of arcs compete for usage in crossover. Any another aspect of this algorithm is executed as specified in [7]. An example of this crossover is represented in the figure below.

Presented approach enables to control the trees’ complexity. Designed self-configuring GA has been used for the purposes of adjustment of trees’ parameters.

Realized as a program system, algorithm has been tested on classification tasks [8]. Australian credit is a task of suspicious bank transactions discovery. This task has 14 variables and 2 classes. German credit is a task of trustworthiness evaluation. This task has 24 variables and

2 classes. Efficiency comparison between proposed algorithm and existing algorithms are shown in the following spreadsheet [9] (table 2).

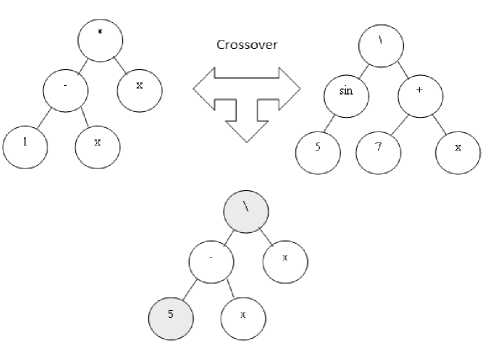
Fig. 4. An example of uniform crossover

Algorithm efficiency criteria:

I _ 1 _ ERROR

n

.

In this formula ERROR is the number of incorrectly classified objects, n is an overall amount of sample. In tab. 2 average values of 50 runs are given. Sample has been separated into 2 groups (test and training samples). Test sample ratio is 20:80. As represented in previous spreadsheet, proposed self-configuring GPA has shown moderate results. So, developed self-configuring algorithm in classification tasks has shown results comparable to existing analogues.

Genetic programming algorithm for artificial neural network design. For the purposes of the automated neural network design it’s necessary to choose the tree neural network encoding method. Binary trees shall encode neural network. In this algorithm the terminal set embraces all input data variable and neurons with different types of activation function. Functional set shall contain following operators:

“+” – operator which allows to form a layer which includes several neurons;

“>” – operator that indicates that “left” sub-tree output data serves as an input data for the “right” sub-tree;

“<” – vice versa.

Illustration of encoding methods is shown below:

In this figure an example of simple ANN encoding by means of tree is given. In this figure, N1 stands for 1- st type neuron (which is selected from the list of activation functions) and ij – j-th input data variable.

Presented algorithm has been implemented in the form of program system (ANN_GP). It’s effectiveness and comparison with existing algorithms is presented below. As stated before, GP designed ANN structure learning procedure is based on GA.

Presented algorithms have been tested on classification tasks [8] in conditions specified above. Efficiency criteria are calculated as in the formula (2).

Algorithms have proved high efficiency in solving classification tasks. Worth noting that, ANN_GA and ANN_GP have shown equal efficiency in Wilcoxon signed-rank test. For such purposes 5 series of tests by 10 runs have been conducted. However, GA computing time has been 3 times longer by average. It can be explained by GA encoding multi-layer perceptron with many connections between neurons. Network training in such case is very consuming in terms of resources.

The test results

Table 2

Algorithm name	Australian credit	German Credit	Algorithm name	Australian credit	German credit
SCGP	0,9022	0,7950	Boosting	0,7600	0,7000
MGP	0,8985	0,7875	Bagging	0,8470	0,6840
2SGP	0,9027	0,8015	RSM	0,8520	0,6770
GP	0,8889	0,7834	CCEL	0,8660	0,7460
Fuzzy classifier	0,8910	0,7940	CART	0,8744	0,7565
C4.5	0,8986	0,7773	MLP	0,8986	0,7618
LR	0,8696	0,7837	GP	0,8874	0,7697
k-NN	0,7150	0,7151

The test results

Table 3

Algorithm name	Australian Credit	German credit	Algorithm name	Australian credit	German credit
SCGP	0,9022	0,7950	Boosting	0,7600	0,7000
MGP	0,8985	0,7875	Bagging	0,8470	0,6840
2SGP	0,9027	0,8015	RSM	0,8520	0,6770
GP	0,8889	0,7834	CCEL	0,8660	0,7460
Fuzzy classifier	0,8910	0,7940	CART	0,8744	0,7565
C4.5	0,8986	0,7773	MLP	0,8986	0,7618
LR	0,8696	0,7837	ANN_GA	0,8994	0,7589
k-NN	0,7150	0,7151	ANN_GP	0,9001	0,7596

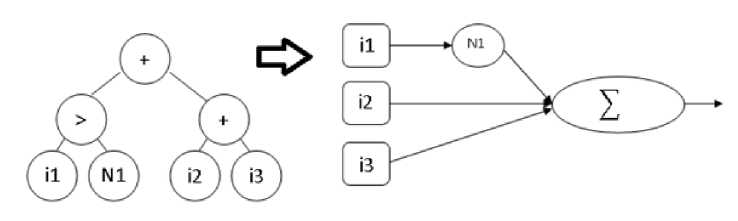
Fig. 5. Neural network encoding example

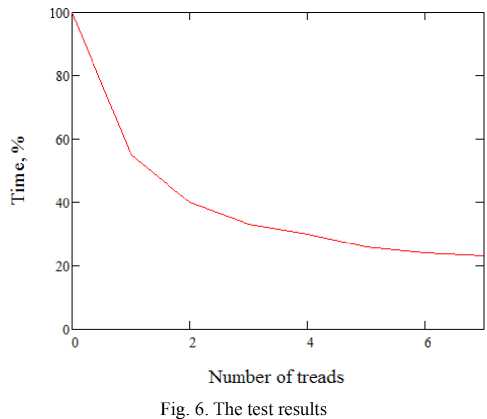
Distributed computing. EA realization by means of distributed computing application is suggested. It means that all node calculations shall be executed by logic cores of computing systems, while algorithm itself shall not be altered. The main idea is that each one of the threads processes certain groups of individuals.

Worth noting that EA are stochastic. Distribute computing shortens the time-consumption without affecting any other criteria. Such effect has been achieved by means of master-thread usage, which was responsible for random number generator. Wilcoxon signed-rank test as well proves that reliability has not been affected.

Test has been conducted on a PC with following specifications:

– Operating System: Microsoft Windows 7;

– CPU: AMD FX8320 (@3.5GHz);

– RAM: 16GB.

Following graph shows dependency of th timeconsumption from a number of logic cores used.

Conclusions. Following algorithms have been developed and implemented: distributed self-configuring GA and GPA. Algorithms have been tested on a series of tasks and proved their effectiveness. Additionally, on ba- sis of these algorithms the new artificial neural network design systems have been developed and tested on classification tasks.

Self-configuration enables to solve one of the actual tasks – genetic operator selection in EA. Distributed computing shortens the time-consumption without affecting efficiency. It might be useful in the case that involves great amount of time being spent on calculation. Judging from presented approaches comparison one should conclude that GPA is preferable in cases of artificial neural network design.