Distributed Traffic Balancing Routing for LEO Satellite Networks

Published Online November 2013 in MECS DOI: 10.5815/ijcnis.2014.01.03

Satellite networks have been an important infrastructure of both Next-Generation Internet (NGI) and Interplanetary Internet (IPN). Compared with the ground networks, satellite networks can provide the extraordinary advantages in global communication, broadcast, space information development, etc. Most satellite networks make use of inter-satellite links (ISLs) to construct a dynamic network, whose characteristics such as the topological dynamics, limited processing facility and storage space, etc., obstruct the effective implementation of conventional routing protocols such as RIP or OSPF. With the rapid development of space technologies, future space communication will be confronted with complex situation. Not only the natural factors such as electromagnetic interference, physical failure and energy limited, but also the factitious behavior such as spatial competition, military strike, etc., might result in the satellite failure, which can bring the significant impact on the communication of satellite networks. First of all, the effects of the failed satellites on communication are global. Once the failed satellites move to a new geographical area where previous satellites are safe, the communication of this area is influenced until the failed satellites move away. Secondly, due to the long renewing cycle and expensive maintenance, the recovery of the failed satellites needs a long time or can not even be completed. Therefore it is a challenge issue to develop the efficient and survivable routing protocols for satellite networks.

So far, many routing schemes have been developed for satellite networks. For the routing algorithms based on virtual topology (VP) [1], [2], [3], the time varying topology is tackled by a discrete time network model. In each time interval, the satellite network is assumed to have a fixed topology. The time interval is determined by the change of the physical topology or other metrics such as propagation delay [1]. For example, the concept of snapshots [2] was introduced to describe the dynamics of LSNs. When a new ISL is added or an already existing ISL is broken, a new snapshot different from the previous one will be formed. However, the number of snapshots in its cycle can be very large as the ISLs change pretty fast when they pass the south and north Polar Regions or switch over the seam, which results in the very large overheads of routing computation and storage. In [4], based on the predictable changes of spacecraft networks, the authors formalize the snapshot concept. Every satellite only stores the differences between adjacent snapshots and the transition rules, so the snapshot transition can be completed automatically by the satellites with low storage overhead. Nonetheless, the snapshot number is essentially unchanged, which means that the frequent routing computation is still unavoidable. With the rapid growth of Internet-based applications, many distributed routing algorithms [5], [6], [7] are presented to forward the packets with the nominal overhead. Since the distributed routing schemes decides the route by the local information, they are just suitable for the case that only a neighboring satellite fails, instead of the case that any satellite may fail at any time. To improve the routing performance, routing protocols based on multi-layered satellite network are proposed [8], [9], [10]. However, these routing protocols only considered the case of random node failures in LEO satellite layer. In fact, if the MEO satellite fails, these routing protocols will collapse. An agent-based load balancing routing (ALBR) [11], [12] is presented for LEO satellite networks, in which mobile agents and stationary agents cooperate to achieve the load balancing routing. However, the case of random node failure is not considered. In this case, the mobile agent does not know the network topology, so it is possible that the mobile agent remove itself before it reaches the destination because of the faulty satellites. From the above statement, it can be seen that the existing routing schemes for satellite networks can’t reach a trade-off between the survivable ability and the routing overheads. The routing protocols based on VP can update routing tables for every snapshot after getting the information of faulty satellites; however, it suffers from the slow reaction and the large computation and storage overheads. Although the distributed routing protocols introduce low computation and storage overhead, the routing survivability is limited. Therefore, it is necessary to develop a routing scheme with low computation and storage overheads and good routing survivability for satellite networks.

In this paper, based on the virtual topology model [13], we propose a new routing protocol for Low Earth Orbit (LEO) satellite networks, called Distributed Traffic Balancing Routing (DTBR). The proposed protocol not only guarantees the routing survivability and provides the ability of traffic balancing, but also result in few additional communication overheads only deriving from the information flooding of failed satellites. The performance of DTBR is also evaluated by simulation.

The rest of this paper is organized as follows: Section 2 presents the system model of LEO satellite networks and Section 3 introduces the virtual topology model for LEO satellite networks. The Distributed Traffic Balancing Routing (DTBR) protocol is proposed in Section 4 and Section 5 presents simulation results. We summarize the paper in Section 6.

• II.    SYSTEM MODEL

The LEO Satellite Network (LSN) is the time varying and predictable network composed of N orbits, each orbit with M satellites. There are two constellation designs for satellite networks: Walker delta and Walker star constellations, which can be denoted by N×M/M/F , where F = 0, . . . , N -1, as shown in Figure 1. For Walker delta constellation, the orbit inclination angle is less than 90°, and the planes are separated from each other with the same angular distance of 360°/ N . For Walker star constellation, the orbit inclination angle is near 90°, and the planes are separated from each other with the same angular distance of 180°/ N . The Inter-plane ISLs connect satellites from different orbits, while the Intra-plane ISLs connect satellites in the same orbit.

In this work, we focus on the LSN with the Walker star constellation, i.e., Polar Orbit satellite networks, where the Intra-plane ISLs are maintained at all times, while the Inter-plane ISLs are shut down in the Polar Regions and re-established outside of the Polar Regions. The satellites between the adjacent 0th and (N-1)th planes move in opposite directions, which results in a called seam existing between the two planes. It is expensive to connect two satellites over the seam [14], so we assume that there are not cross-seam ISLs. The LSN can be formalized as a time graph G(t)=(V(t),E(t)), where V(t) and E(t) are respectively the set of nodes and edges at time t. In the random case, any satellite might fail at any time, so |V(t)| is not always equal to N×M. The concept of snapshot [2] can capture the dynamics of G(t). In this concept, once a link is re-established or a link is closed, a snapshot different from the previous one is formed. For the periodicity of satellite movement, the LSN topology can be described by a sequence of snapshots. The number of snapshots in an orbit cycle is very large because of the frequent changes of the Interplane ISLs in the Polar Regions.

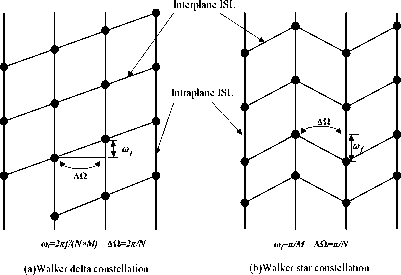
Figure1 Satellite networks constellation

• III.    VIRTUAL TOPOLOGY

• A.    Virtual topology and address mapping

Based on the Earth-fixed footprint mode of the satellite antenna systems on Polar orbit LSN, the authors formalized the LSN as a virtual topology FVT [13], Compared with the physical topology of LSN, the FVT exhibits some important advantages such as few snapshots, well-proportioned snapshot length, avoidance of path stretch and contraction, which is better for the realization of routing protocols. Let G_v(t) denote the topological graph of FVT, firstly, two basic mappings are necessary for performing the routing protocol on FVT : the mapping from the LSN to FVT can construct G v (t) , and the mapping from the earth to FVT can determine the logical location of the earth terminals. We use a pair of ordered integers (x(c), y(c)) to identify the actual location of satellite c on the LSN, where x(c), for x(c) = 0,…, N-1 is the orbit number and y(c), for y(c) = 0,…, M-1 is the satellite number. Let α(s,t) and β(s,t) denote the logical location of node s at time t , where t is the time that the satellite has moved. The logical location of any satellite (x(c), y(c)) at time t is described as follows:

a ( c , t ) = x ( c )

в c , t ) = [ y ( c ) + [ [ w ( t %T )] / (2 n / M ) J ]% M

Where ω , T and M are the angle velocity of the satellites, the orbital cycle, and the satellite number of the plane, respectively.

Since G_v(t) is independent of the rotation of the earth, we assume the geographic coordinate system is constructed on G v (t) at t=0 . The mapping from the earth to G v (t) can be achieved by computing new geographic location on G v (t) at any time t . Let lon(E,t) and lat(E,t) respectively denote the longitude and latitude of the earth node E at time t on G_v(t) , which are computed as follows:

lon, = [ lon ( E , 0) + ( t %T >']%(2 л )

lon ( E , t ) = -

2 n - lon

lont

lon, > П lon, <  П

lat ( E , t ) = lat ( E ,0)

Where ω′ and T′ are the angle velocity and the cycle of the rotation of the earth, respectively. According to Formula (2), the logical location of any node E on the earth at time t is computed below.

• 5:  Set all intraplane VL s from (α(c, t₀), β(c, t₀)) to its

neighbors to true ;

• 6:    if (α(c, t 0 ), β(c, t 0 )) and its neighbors of different planes are not affected by latitude threshold

• 7:       set their VLs to true ;

• 8:    else

• 9:       set their VLs to false ;

• 10:    end if

• 11:    set all VLs from (α(c, t), β(c, t)) to its all neighbors to false ;

• 12:    t₀← t;

• 13:    else

• 14:    set all VLs from (α(c, t), β(c, t)) to its all neighbors to false ;

• 15:    end if

• 16:    end if

a( E, t) = Xo (lon (E, t))

в( E, t) = Уо (lon (E, t), lat ( E, t))

Where X 0 (lon) and Y 0 (lon,lat) is the mapping from any location on the earth to G v (t) at t=0 , which can be computed beforehand.

• B.    Virtual snapshot transition

According to the properties of FVT [13], a prominent superiority of the FVT is the maximal number of the snapshots is not more than the footprint number of a plane no matter how many faulty satellites happen. Besides, for the strict orbital movements of all satellites, the transition between virtual snapshots has also the specific regularity. Since the FVT can result in few snapshots and its topological dynamics can be predetermined due to the strict orbital movement of all satellites, it is possible to realize a fully distributed routing protocol. In fact, every satellite can independently calculate current G v (t) at any time t as long as it owns the information of all failed satellites, which includes two parts: the information flooding of failed satellites and execution of a snapshot transition algorithm. The first part enables every safe satellite to get the location of all failed satellites, described as follows: every satellite reports all failed satellites it knows to its safe neighbors, and the same information is only sent once; for the fast updating, the flooding message is run by the highest priority queues. When a safe satellite gets the logical location of all failed satellites by Formula (1), the snapshot transition is executed by the following Algorithm.

Snapshot Transition ST( c , t₀ , t )

Takes failed satellite c , the time t₀ of the last snapshot transition and current time t as input

• 1:    if running snapshot transition first time

• 2:  t 0 ← t

• 3:    end if

• 4:    if β(c, t 0 )!= β(c, t)

The snapshot transition is executed once the satellite switches to next logical region . Algorithm 1 firstly judges whether the snapshot transition was run first time. If it holds, the transition will be executed by Step 14; otherwise the transition includes two processes: the VL restoration of time t₀ and the VL destruction of current time t , which are executed by Step 5~10 and Step 11, respectively. A safe LEO satellite needs to run Algorithm 1 N_F times when it enters a new logical region , where N F is the number of all failed LEO satellites.

• IV.    ROUTING PROTOCOL

In this section, we will present a new routing protocol with traffic prediction, called Distributed Traffic Balancing Routing (DTBR), which not only provides good routing survivability with low load, but introduces an ISL cost factor to avoid congestion and balance the traffic. Besides, the protocol will not result in any additional communication overheads except the flooding of failed satellites.

• A.    ISL cost

For the routing quality, a cost factor λ based on the empirical dispersion of global hot spot zones is introduced to the ISL cost, which dynamically adjusts the traffic distribution for traffic balancing. The ISL cost metric is presented as:

ISL cos t = A PD (VL) (4)

Where PD(VL) present the propagation delay of virtual link VL . Let δ(F) denotes the center of logical region F . PD(VL) is defined as follows.

Definition 1 Let Vl (F i,j ,F k,r ) be the virtual link between logical region F_i, j and F_k,r in G_v(t). The delay function PD( Vl (F_i, j ,F_k,r)) is defined as:

propagation delay from 6 ( F ) to £ ( F_{k r}),

PD ( V ( F , j , F k , r )) =

3 ISL(S(F j ),S(F k , r )) л

(0 <  i, k <  N ) л (0 <  j, r <  M ) ^              , otherwise

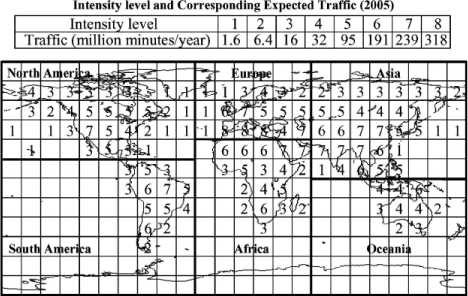
Due to population dispersion, economy and technology development, most of hot spots locate at the Northern Hemisphere, especially within the scope of 50°N [15]. The forecasted traffic over LEO satellite systems in 2005 is illustrated in Figure 2. The ISL cost modification factor in [11] only considers the north hemisphere. Since the south hemisphere still has some hop spots, we modify the ISL cost modification factor as follows:

" etna /90 e la^ /90

x = ^

-- \lat |/90

0 <  lat <  50

( lat <  0) л (( - 80° <  lon <- 40°)

v ( - 15° <  lon <  50°) v                     ⁽⁶⁾

(110° <  lon <  150°))

otherwise

Where lat and lon respectively represent the latitude and longitude of the LEO satellite. Based on λ factor, the ISL cost in hot spot zones tends to increase, and in nonhot spot zones tends to decrease.

• B.    Routing calculation

Since any LEO satellite can automatically get current FVT and the ISL costs, the routing table can be calculation independently by every LEO satellite anytime. For the earth’s rotation, the hot spots will continuously switch to different logical regions . To timely reflect the traffic change on FVT, once the LEO satellite switches to next logical region , its routing table should be updated, which is calculated as follows:

Step 1 : Once the satellite switches to next logical region , if failed satellites exist, every LEO satellite automatically finishes snapshot transition by Algorithm 1 ; otherwise its snapshot keeps constant in terms of the property of FVT [13].

Step 2: Every LEO satellite computes ISLcost of all ISLs by formula (4). In fact, PD(VL) of all virtual links is only computed once if there is not the failed satellites; otherwise only the virtual links affected by the failed satellites are set to ∞. For balancing factor λ, every satellite needs to compute the geographical coordination of all satellites on the earth, so the time complexity is O(n), where n is the number of all safe satellites.

Step 3 : Once the satellite gets the ISL costs of all ISLs, the routing table is updated as follows:

Routing updating

• 1:    var U(F,S) /* The updating mark of virtual snapshot S in footprint F */

• 2:    var R(F,S) /* The routing computation mark of footprint F for virtual snapshot S */

• 3:    if (U(F,S)) // The virtual snapshot S in footprint

F is updated in current footprint

• 4:             if (R(F,S)) // The routing table for new

virtual snapshot S in footprint F has been updated

• 5:                       return

• 6:               else

• 7:                    UpdateRoutingTable(F,S)

• 8:                     R(F,S)=true

• 9:              end if

• 10:           U(F,S)=false

• 11:   else

• 12:             if (R(F,S))

• 13:                      return

• 14:             else

• 15:                   UpdateRoutingTable(F,S)

• 16:                    R(F,S)=true

• 17:             end if

• 18:   end if

The routing table is calculated by Dijkstra algorithm with time complexity O( n ²), where n is the number of all safe satellites.

• C.    Congestion avoidance

The DTBR uses the traffic prediction factor λ to avoid congestion, whereby the traffic deviates from the hot spot zones to non-hot spot zones. In this way, the congestion probability is decreased. However, the congestion still may occur when the burst traffic is generated. In this case, the ELB scheme [16] is used, whereby a congested satellite sends a signal to its neighboring satellites to decrease their sending rates, and its neighbors search for alternate paths.

• D.    Satellite failure

For satellite failures, the end-to-end path in LSN does not always exist. For example, once failed satellites move to source or destination location, data transmission between them will fail. In this case, two methods can be considered: store-carry-forward mechanism of DTN [17] and source waiting. In the first method, when the end-to-end path does not exist, the packets can be routed to an intermediate node where the packet will wait until there is a feasible path. Due to the predictability about future topology, the packets can be forwarded successfully as long as the end-to-end path exists in the future. The shortage of this method lies in that it presents high requirement on the satellite’s storage space. For the second method, before the earth terminal sends the packets, it enquires of the current satellite whether the destination is reachable. If yes, the packets will be forwarded; otherwise the terminal will wait until a satellite can serve it and a feasible path exists. Since the waiting delay is far greater than the transmission delay, and most existing LEO satellites are limited to the storage space, the second method is a suitable selection.

• V.    PERFORMANCE EVALUATION

  To demonstrate the effectiveness of our routing schemes, three main experiments are constructed based on the ns2 simulator. Four routing protocols are involved in the experiments as comparison, which include DTBR without source waiting, DTBR with source waiting, Datagram Routing Algorithm (DRA) [5] and Satellite Snapshot Routing (SSR). In SSR, the routing table with minimal propagation delay is calculated by Dijkstra algorithm for every snapshot. In the simulation scenario, a polar orbit LEO satellite constellation with 12 planes and 24 satellites in each plane is generated. The ISL capacity is 2.5Mb and latitude threshold is 75°. In all experiments, the source-destination pair is located at (37.9°N, 31.6°E) and (30°S, 100°W), and simulation time is 6794 s, i.e., an orbit cycle.

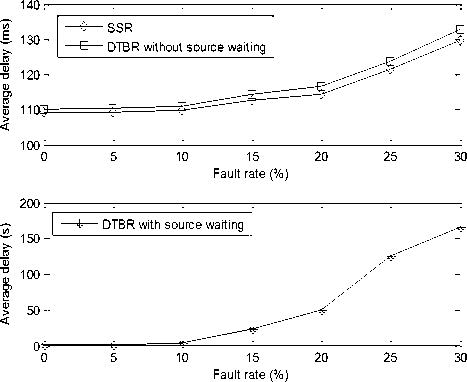
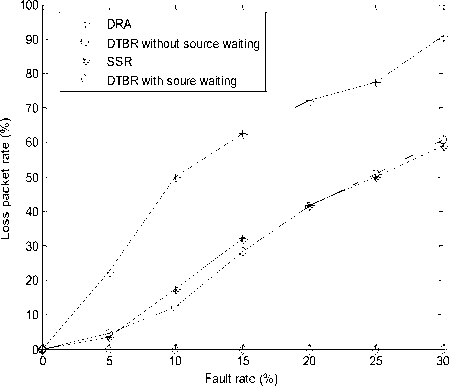
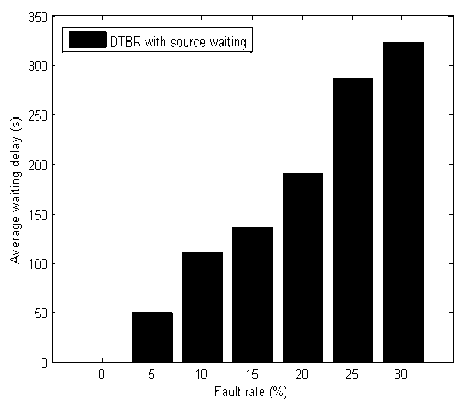
To evaluate the routing survivability, we generate randomly 0~30% failed satellites in the system by the interval 5% and set a low data rate with one packet per 30s. Figure 3 illustrates the loss packet rate. Since DRA forwards the packets in terms of local information, its loss packet rate dramatically increases as the fault rate is raised. On the contrary, for DTBR and SSR, the packet is discarded if and only if the end-to-end path does not exist. DTBR with source waiting can successfully route all packets even if the fault rate reaches 30%. Theoretically, as long as there is a safe satellite, the packets can be forward successfully with the arbitrary delay since the satellite might move to any location on the earth. As shown in Figure 4, both DTBR without source waiting and SSR have the similar average end-to-end delay. For the predominant waiting delay, it is inevitable that DTBR with source waiting suffers from large end-to-end delay as fault rate is raised. Figure 5 illustrates the changes of average waiting delay in different fault rate.

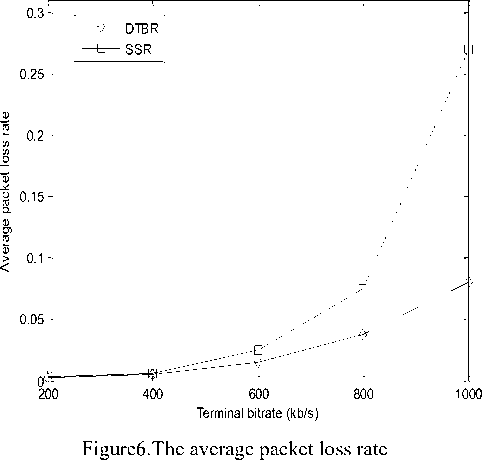
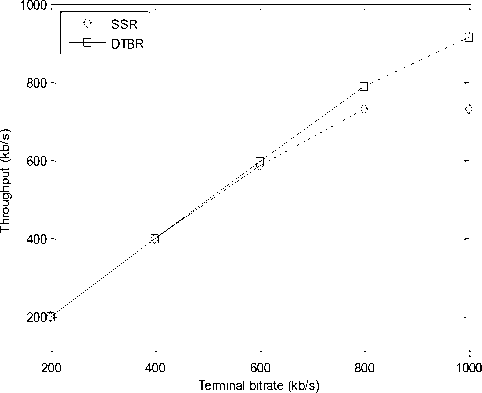
To evaluate the throughput, all satellites over hot spot zones generates on/off traffic whose Pareto distribution with the average on/off durations equal to 100 ms. The traffic bit rate of source node is varied from 200 to 1000 by 200kb/s. Figure 6 presents the average packet loss rate of DTBR and SSR. Due to ISL cost factor λ, the traffic can be detoured from the hot spots by DTBR, which decreases the probability of packet loss. Figure 7 shows the throughput of DTBR and SSR. It is obvious that DTBR has a better throughput than SSR for less packet loss rate when the terminal bit rate is increased.

• VI.    CONCLUSIONS

Based on the virtual topology model [13], this paper proposes a distributed traffic balancing routing protocol for LEO satellite networks, which provides the routing survivability, the ability of traffic balancing, and few additional communication overheads only deriving from the information flooding of failed satellites. Simulation results demonstrate positive conclusions of the proposed protocol.

ACKNOWLEDGMENT

This work was supported by the National Basic Research Program of China (973 Program) (Grant No: 2012CB821206), National Natural Science Foundation of China (Grant No: 60903184, 61073167), the National High Technology Development Program of China (Grant No: 2011AA010704), Beijing Natural Science

Foundation (Grant No: 4122037), National science and technology support program of China (Grant No: 2011BAH15B08).